【智能算法】黄金正弦算法（GSA）原理及实现

---

1.背景

2017年，Tanyildizi等人受到正弦函数单位圆内扫描启发，提出了黄金正弦算法（Golden Sine Algorithm, GSA）。

2.算法原理

2.1算法思想

GSA来源于正弦函数单位圆内扫描类似于待优化问题解的空间搜索，并通过黄金分割率缩小搜索空间以逼近算法最优解。

2.2算法过程

黄金分割系数：

GSA在位置更新过程中引入黄金分割系数 x1 、x2 使“搜索”和“开发”达到良好的平衡，这些系数缩小了搜索空间引领个体趋近最优值：
x 1 = a ⋅ ( 1 − τ ) + b ⋅ τ x 2 = a ⋅ ( τ + b ⋅ ( 1 − τ ) (1)

$$\begin{array}{rl}{x_{1}=a\cdot(1-\tau)+b\cdot\tau}\\{x_{2}=a\cdot(\tau+b\cdot(1-\tau)}\end{array}$$ \tag{1} x1​=a⋅(1−τ)+b⋅τx2​=a⋅(τ+b⋅(1−τ)​(1)
其中，a,b为 黄金分割比率搜索初始值，论文中a = -π、b = π，τ为黄金分割比率：
$$\tau =(\sqrt{5}-1)/2\text{\hspace{1em}(2)}$$

位置更新：

V i t + 1 = V i t ⋅ ∣ sin ⁡ ( r 1 ) ∣ − r 2 ⋅ sin ⁡ ( r 1 ) ⋅ ∣ x 1 ⋅ D i t − x 2 ⋅ V i t ∣ (3)

$$\begin{aligned}V_i^{t+1}&=V_i^t&\cdot\mid\sin(r_1)\mid-r_2&\cdot\sin(r_1)&\cdot\mid x_1&\cdot D_i^t-x_2&\cdot V_i^t\mid\end{aligned}$$ \tag{3} Vit+1​​=Vit​​⋅∣sin(r1​)∣−r2​​⋅sin(r1​)​⋅∣x1​​⋅Dit​−x2​​⋅Vit​∣​(3)

伪代码：

3.结果展示

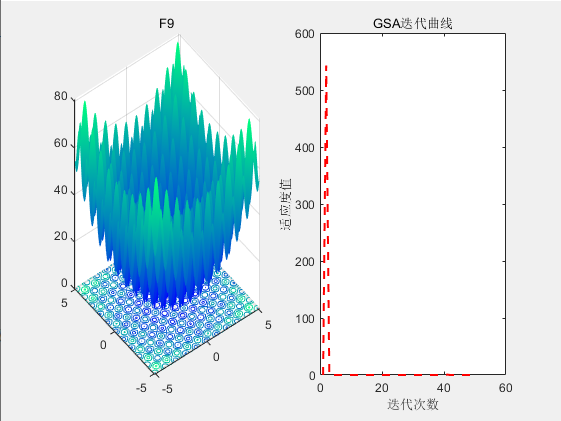
4.参考文献

[1] Tanyildizi E, Demir G. Golden sine algorithm: a novel math-inspired algorithm[J]. Advances in Electrical & Computer Engineering, 2017, 17(2).