热门标签
热门文章
- 1网络安全之IPSEC路由基本配置_ipsec 喷段路由
- 2网络安全初学者必备的60个工具,零基础入门到精通,收藏这一篇就够了_网络发现工具
- 3手把手教你如何使用GitHub的服务器搭建自己的简单网站_github搭建网站 dns
- 4浅谈鸿蒙HarmonyOS:鸿蒙开发,对于前端开发来说,究竟是福还是祸?_鸿蒙os与c#
- 5python数据分析:客户价值分析案例实战_电信类数据分析
- 6Python tkinter(四) 文本框(Text)组件的属性说明及示例_python text
- 7安全模型-自主访问控制/强制访问控制_强制访问控制模型与自主访问
- 8清华学霸告诉你:如何自学人工智能?_学习机器学习需要先把算法原理搞懂吗
- 9三十八篇:架构大师之路:探索软件设计的无限可能
- 10MIT 6.S081学习笔记_fail: sysinfo succeeded with bad argument这个问题是怎么回事
当前位置: article > 正文
ARIMA参数判定_如何通过acf和pacf判断arima的参数
作者:盐析白兔 | 2024-07-03 01:24:51
赞
踩
如何通过acf和pacf判断arima的参数
前言:在分析时间序列数据的ARIMA模型中,最重要的一步便是模型参数的判定。存在两种选定模型参数的方法,一是,借助ACF、PACF图的截尾、拖尾的阶数以及AIC、BIC等信息准则;二是,迭代p、q的值,并结合信息准则
拖尾和截尾
截尾:自相关函数(ACF)或偏自相关函数(PACF) 在某阶后突趋于0。
出现以下情况,通常视为(偏)自相关系数d阶截尾:
- 在最初的d阶明显大于2倍标准差范围
- 之后几乎95%的(偏)自相关系数都落在2倍标准差范围以内
- 且由非零自相关系数衰减为在零附近小值波动的过程非常突然
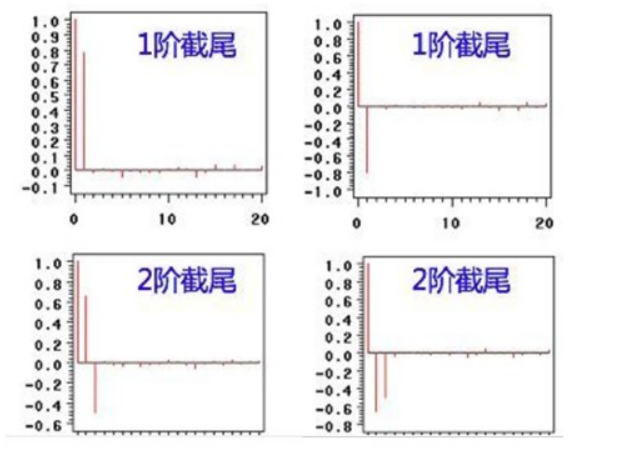
拖尾:ACF或PACF始终有非零取值,某阶后在0附近波动没有趋于0的趋势
出现以下情况,通常视为(偏)自相关系数拖尾:
- 如果有超过5%的样本(偏)自相关系数都落入2倍标准差范围之外
- 或者是由显著非0的(偏)自相关系数衰减为小值波动的过程比较缓慢或非常连续。
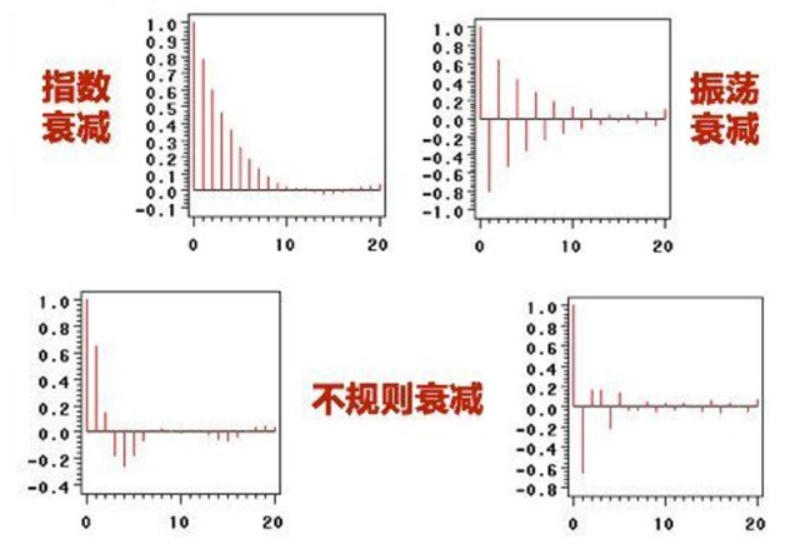
实例:拖尾和截尾阶数判断
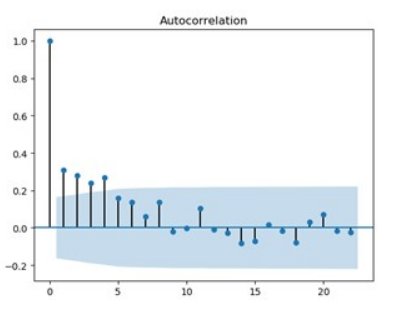
4阶后截尾:ACF图在第4阶后衰减,并在标准差2倍范围内,在0附近波动
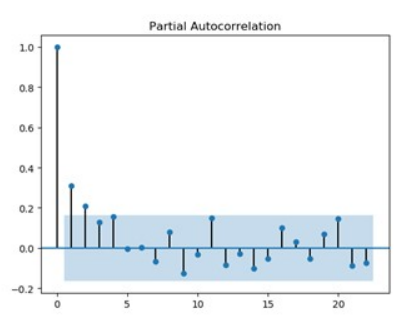
3阶后拖尾:PACF图在第2阶后衰减,不趋于0
ARMA模型的定阶级及参数估计
人工判断
根据ACF、PACF图像是否截尾或拖尾及其结束判断合适的参数
| 模型 | ACF | PACF |
|---|---|---|
| AR§ | 拖尾 | p阶后截尾 |
| MA(q) | q阶后截尾 | 拖尾 |
| ARMA(p, q) | q阶后截尾 | p阶后截尾 |
注:
-
拖尾包含了k阶后拖尾
-
AMIMA和ARMA的区别:前者包含了后者,前者多一步差分操作
循环迭代
当ARMA模型的阶数越高,其描述对象样本的能力就越强。但是阶数越高,参数也就越多,容易造成过拟合的现象。因此我们需要找一个度量工具,来确定最佳的阶数。用的较为广泛的工具为赤池信息量准则(Akaike information criterion,简称AIC)以及贝叶斯信息量准则(Bayesian information criterion,简称BIC)。
参考文章
时间序列学习(5):ARMA模型定阶(AIC、BIC准则、Ljung-Box检验)_lucialucia的博客-CSDN博客_arma定阶原则
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/盐析白兔/article/detail/781507
推荐阅读
相关标签




