【基于分治的两大重点排序算法】快速排序、归并排序；特定场景效率极高的排序——计数排序_基于分治算法的排序

---

前言

上一篇博客中介绍了基于比较的排序中的前五种排序 – 常见排序算法
这次主要介绍两大最常考和也是最重要的排序——快速排序和归并排序。除了这两个排序外，还要介绍一个非基于比较的，好理解的，又在特定场景有奇效的计数排序。

---

一、快速排序

快速排序是一种常用的排序算法，是一种基于分治的算法，其平均时间复杂度为O(nlogn)。
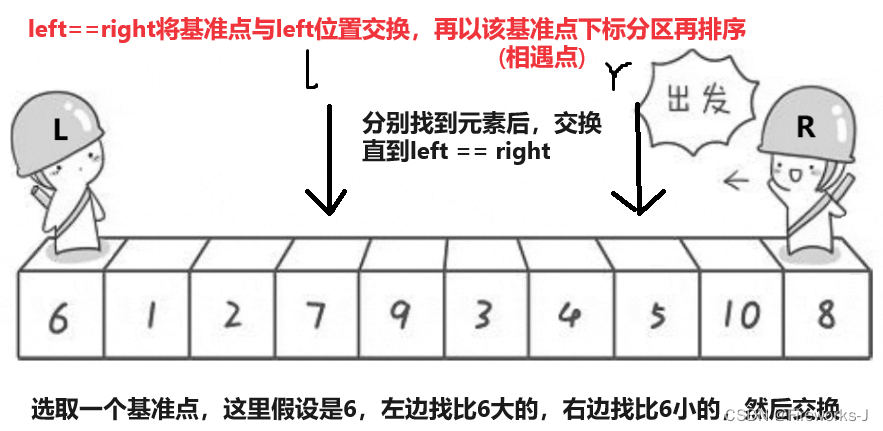
它的基本思想是通过选取一个基准元素，将待排序序列分割成两个子序列，其中一个子序列中的元素都小于等于基准元素，另一个子序列中的元素都大于等于基准元素。然后递归地对子序列进行排序，最终得到有序的序列。

快速排序经过不断的优化，衍生出了很多的方法，如单边快排（也称为普通快排），双边快排（也称为双向快排或快速排序2.0）。这里主要介绍效率较高的双边快排。

双边快排（也称为双向快排或快速排序2.0）使用两个指针，一个从左往右遍历元素，一个从右往左遍历元素，在遍历过程中不断交换位置，直到两个指针相遇，然后将基准元素放在相遇的位置上。这种方法可以提高分区的效率，因为它同时处理了左边和右边的元素。

对快速排序有一定了解后，可以先列出代码执行流程

    //快速排序
    public static void quickSort(int[] array) {
        quick(array, 0, array.length - 1);
    }

    private static void quick(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }
        //得到相遇点进行分区
        int pivot = partition(array, left, right);
        quick(array, left, pivot - 1);
        quick(array, pivot + 1, right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

• 主体的代码逻辑就在partition(array, left, right)这个方法中。以基准点进行分区操作，说明基准点的选择对效率的影响很大，普通快排中默认第一个元素或者最后一个元素为基准点。而为了减少以基准点分区导致分区极度不平衡的情况，就出现了三数取中和随机基准点的优化方案。

1.三数取中法

三数取中的过程很简单，因此我们仅简单文字介绍三数取中法：

1. 选择序列的开头、结尾和中间位置的三个元素。
2. 取这三个元素中的中值作为基准元素。
3. 将基准元素放在序列头部，也就是left位置，然后按照基本快速排序的方法进行排序。

2.随机基准点

随机基准点也很简单，就是用Random生成，需要注意的是生成的这个随机基准点应在子区间的范围内，而这个范围是 – 区间长度 + left，可以仔细想想为什么是这样表示。

直接先看完整代码：

    //快速排序
    public static void quickSort(int[] array) {
        quick(array, 0, array.length - 1);
    }

    private static void quick(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }
        //得到相遇点进行分区
        int pivot = partition(array, left, right);
        quick(array, left, pivot - 1);
        quick(array, pivot + 1, right);
    }

    private static int partition(int[] array, int left, int right) {
        //随机基准点--区间长度 + left
        int pivot = new Random().nextInt(right - left + 1) + left;
        swap(array, left, pivot);
        int tmp = array[left];
        int l = left;
        int r = right;
        //右边找比基准点小的，左边找比基准点大的，进行交换。最后它们相遇的位置就是基准点位置
        while (l < r) {
            while (l < r && array[r] >= tmp) {
                r--;
            }
            while (l < r && array[l] <= tmp) {
                l++;
            }
            if (l < r) {
                swap(array, l, r);
            }
        }
        //此时l == r，与基准点交换，返回l或r
        swap(array, left, l);
        return l;
    }

    private static void swap(int[] array, int i, int j) {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

几个注意点：

1. 内层right和left找元素时同样需要保证left < right，因为基准点左边都放比他小的，右边放比他大的。如果少了这个条件，可能就将较大值放到分区左边，较小值放到分区右边了。
2. 先从right开始找的原因：right找小值，left找大值，如果left先走，可能相遇时left和right这个位置值是比基准点大的，此时退出循环left和基准点交换，就将大值放到了基准点的左边了。

3.处理重复优化

• 为什么要处理重复？前面的代码会有一个问题，当数组元素全都是同一个数时（LeetCode912用例），right直接走到和left相遇了，这又导致了分区极度不平衡。

这里LeetCode的最后一个用例是一连串的2，就导致快速排序的效率极低！
在上面的代码中，我们遇到与基准点重复的元素时，默认跳过他。而优化方案就是我们遇到重复元素了也停下来，对重复元素也进行一个交换，并且不找相遇点，而是让left正好大于right。这样的好处就在于当都是重复元素时，它们会在数据中间停下来，使分区依然平衡。我们仅改动partition方法里面的代码即可。

    private static int partition2(int[] array, int left, int right) {
        //随机基准点--区间长度 + left
        int pivot = new Random().nextInt((right - left + 1)) + left;
        swap(array, left, pivot);
        int tmp = array[left];
        int l = left + 1;
        int r = right;
        //右边找小于等于基准点，左边找小于等于基准点，进行交换。
        while (l <= r) {
            while (l <= r && array[r] > tmp) {
                r--;
            }
            while (l <= r && array[l] < tmp) {
                l++;
            }
            if (l <= r) {
                swap(array, l, r);
                l++;
                r--;
            }
        }
        //此时r < l，r的元素是小的，与基准点交换，返回r
        swap(array, left, r);
        return r;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

注意：这里返回的是right，原因是此时r 位置正好< l，r在分区左边了，是小的，与基准点交换，返回r

通过以上优化，快速排序在LeetCode912的通过时间如下：

时间复杂度：O（N*logN） 空间复杂度O（logN）

---

二、归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

1. 递：不断将数组切分成两部分，直到每个区间长度为1。
2. 归：合并切分好的两个区间，并排序，使各区间有序。

1.递归（自上至下）

    //归并排序
    public static void mergeSort(int[] array) {
        split(array, 0, array.length - 1);
    }

    private static void split(int[] array, int left, int right) {
        if (left == right) {
            return;
        }
        int mid = left + (right - left) / 2;
        //左边
        split(array, left, mid);
        //右边
        split(array, mid + 1, right);
        //合并排序
        merge(array, left, mid, mid + 1, right);
    }

    private static void merge(int[] array, int i, int iEnd, int j, int jEnd) {
        int[] a = new int[jEnd - i + 1];
        int k = 0;
        int left = i;//记录数组的左边界
        while (i <= iEnd && j <= jEnd) {
            if (array[i] < array[j]) {
                a[k++] = array[i++];
            } else {
                a[k++] = array[j++];
            }
        }
        //排完剩下的数组
        while (i <= iEnd) {
            a[k++] = array[i++];
        }
        while (j <= jEnd) {
            a[k++] = array[j++];
        }
        //最后a数组拷贝回array数组
        System.arraycopy(a, 0, array, left, k);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

注意点 ：合并的过程就是合并两个有序数组的解法 88. 合并两个有序数组
这么看归并排序也简单，有一点问题，就是当子序列排好序后，我们应该将其拷贝到数组正确的位置。
代码中用left记录了当前子序列的左边界，最后用System.arraycopy(a, 0, array, left, k);将a数组所有元素从array的left位置开始拷贝。
还有一点，在我提交LeetCode时出现了超出时间限制的情况，我找了半天没发现错误，结果就是在merge方法中创建a数组时，我每次new了一个array.length，改成jEnd - i + 1就跑过了。所以以后需要多次使用一个数组长度时，用变量保存是很有必要的。

---

2.非递归（自下至上）

非递归代码就是以分区区间长度为1开始分区，分好区后进行排序。

    //归并排序(非递归)
    public static void mergeSortNor(int[] array) {
        int n = array.length;
        //width表示每次分组各数组的元素个数 1->2->4......
        for (int width = 1; width < n; width *= 2) {
            //left表示每次分组的左边界 left += 2 * width 表示每个待排序区间的元素个数
            for (int left = 0; left < n; left += 2 * width) {
                //防止mid和right越界
                int mid = Math.min(n - 1, left + width - 1);
                int right = Math.min(n - 1, mid + width);
                if (left != right) {
                    merge(array, left, mid, mid + 1, right);
                }
            }
        }
    }
    
    private static void merge(int[] array, int i, int iEnd, int j, int jEnd) {
        int[] a = new int[jEnd - i + 1];
        int k = 0;
        int left = i;//记录数组的左边界
        while (i <= iEnd && j <= jEnd) {
            if (array[i] < array[j]) {
                a[k++] = array[i++];
            } else {
                a[k++] = array[j++];
            }
        }
        //排完剩下的数组
        while (i <= iEnd) {
            a[k++] = array[i++];
        }
        while (j <= jEnd) {
            a[k++] = array[j++];
        }
        //最后a数组拷贝回array数组
        System.arraycopy(a, 0, array, left, k);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

只有一个注意点，mid和right的下标要计算准确。数组个数为奇数个时，mid和right会超出数组长度，如果超出就要取length-1。这里可能出现 left == right 即只有一个元素的情况，但这个优化效果不明显。

时间复杂度：O（N*logN） 空间复杂度O（N）

---

三、计数排序

思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。 这里实现的是简易版本
操作步骤：

1. 找出待排序序列中的最大值和最小值。
2. 创建一个计数数组，长度为最大值与最小值之差加1，用来统计待排序序列中每个元素出现的次数。
3. 根据统计的结果将序列回收到原来的序列中

代码很简单

    //计数排序
    public static void countSort(int[] array) {
        //1.确定范围
        int max = array[0];
        int min = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if (array[i] < min) {
                min = array[i];
            }
        }
        //2.根据范围创建count数组 并统计array元素出现个数到count数组
        int[] count = new int[max - min + 1];
        for (int num : array) {
            count[num - min]++;
        }
        //3.根据count数组，得到排序完成的结果
        int k = 0;
        for (int i = 0; i < count.length; i++) {
            while (count[i]-- > 0) {
                array[k++] = i + min;
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

注意点：以（遍历到的值-min）这个下标来记录元素出现个数，最终赋值给array的值是当前下标+min。

计数排序的时间复杂度是O(n+k)，其中n是待排序序列的长度，k是计数数组的范围（即最大值与最小值之差加1）。由于计数排序需要额外的空间来存储计数数组和临时数组，因此在空间复杂度方面稍高：O（范围）。 计数排序适用于元素范围较小的序列，当元素范围较大时，建立计数数组会耗费太多空间。

而他让我惊讶的一点是，LeetCode这题的用例元素范围可能分散不大，使这个计数排序跑出来的成绩遥遥领先。

---

总结

能通过 LeetCode912排序数组 的各种排序总体情况如下：