[ML]（回归和分类）_ml*;.[]'.

---

该篇是李宏毅2017机器学习课程的学习笔记，主要参考LeeML

误差从哪来？

Error的来源

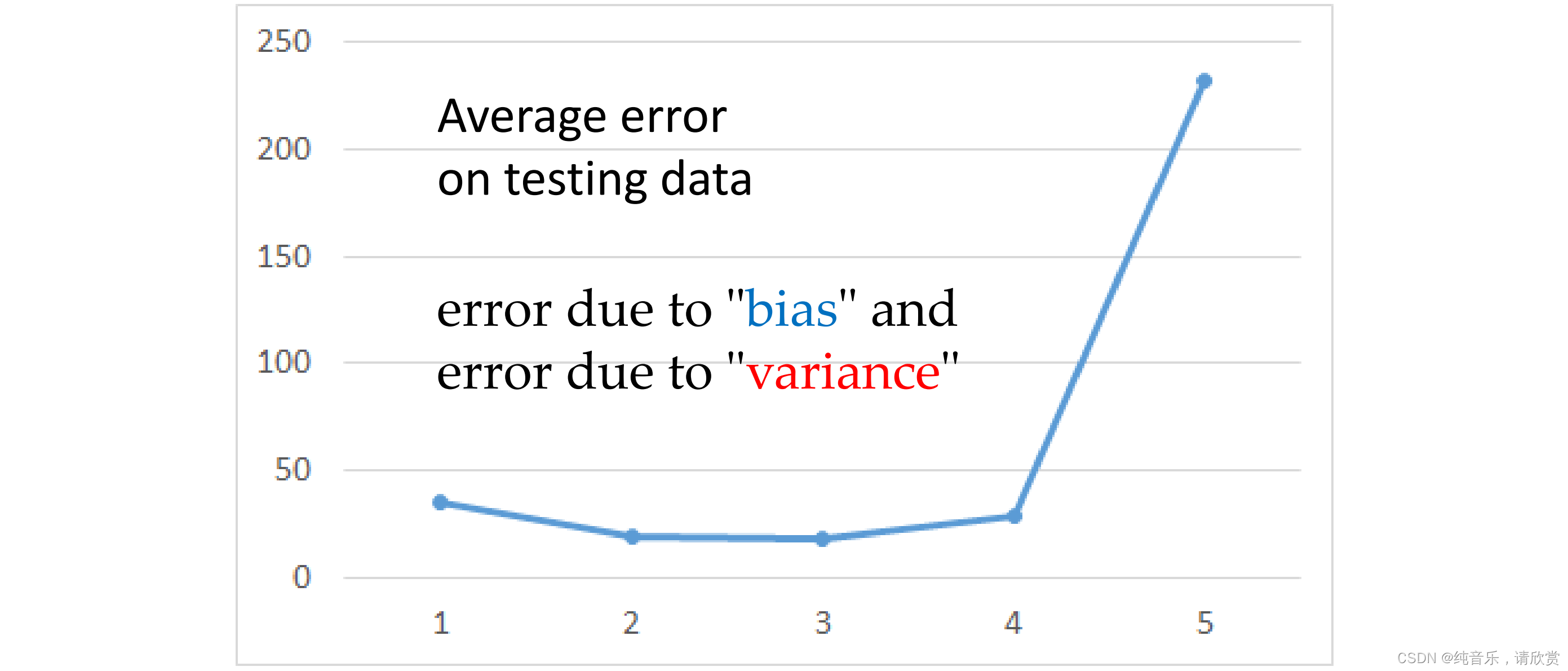
从上节课测试集数据来看，Average Error 随着模型复杂增加呈指数上升趋势。更复杂的模型并不能给测试集带来更好的效果， 而这些 Error 的主要有两个来源，分别是 bias 和 variance。

首先 Error = Bias + Variance

Error反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

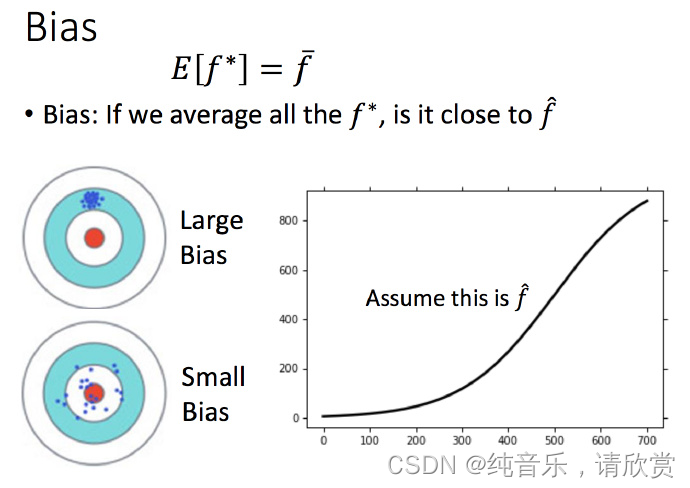
估测

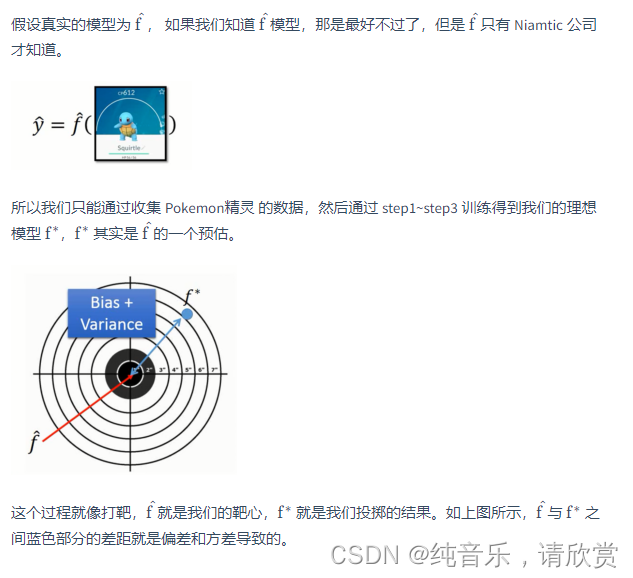
估测变量x的偏差和方差

评估x的偏差：

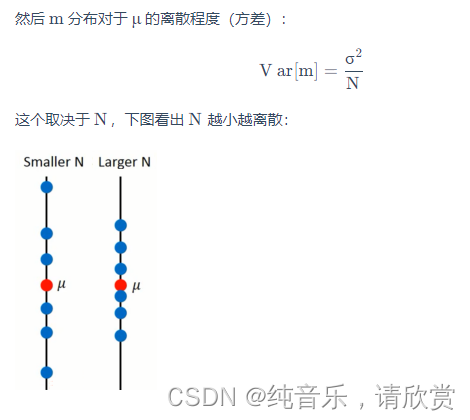
估测变量x的方差

如何估算方差呢？

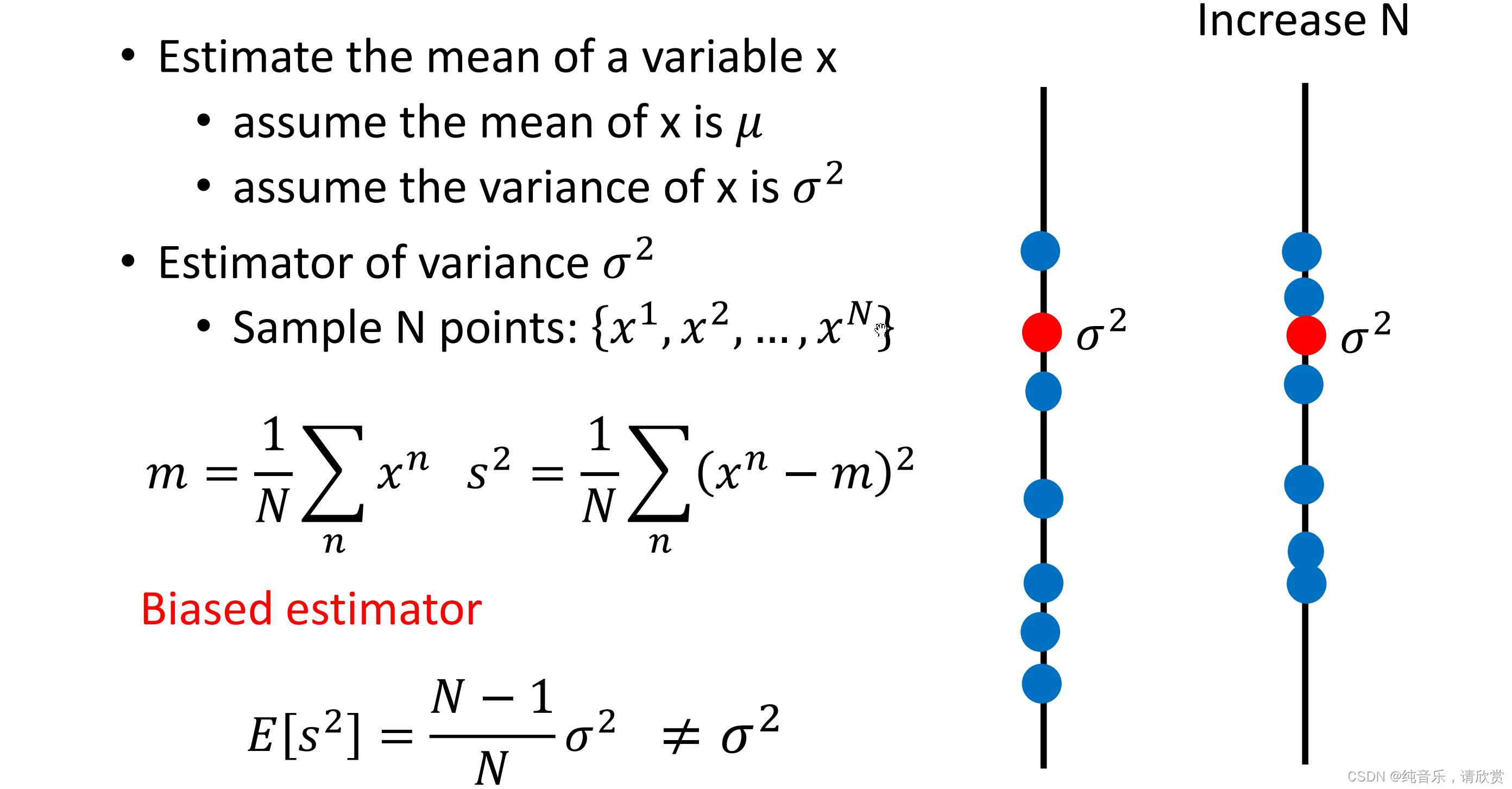
为什么会有很多的模型?

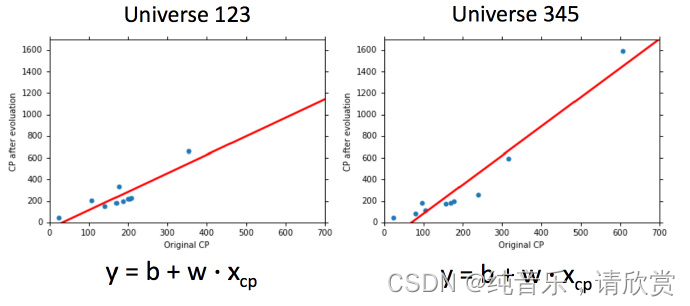
讨论系列02中的案例：这里假设是在平行宇宙中，抓了不同的神奇宝贝

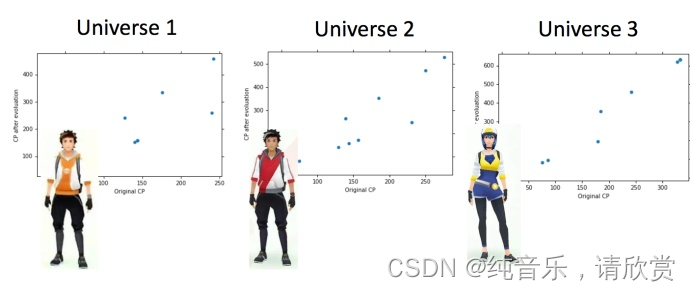
用同一个model，在不同的训练集中找到的 f^∗ 就是不一样的

这就像在靶心上射击，进行了很多组（一组多次）。现在需要知道它的散布是怎样的，将100个宇宙中的model画出来

考虑不同模型的方差：

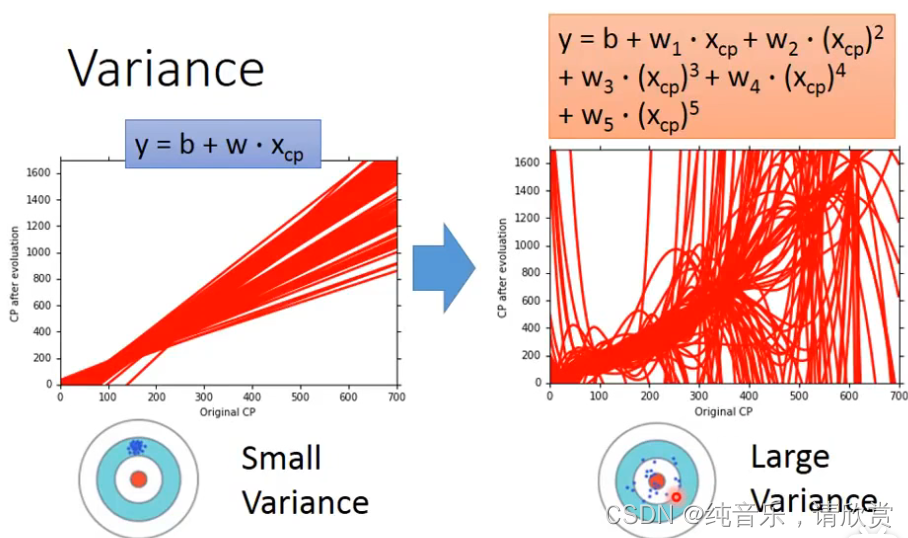
一次模型的方差就比较小的，也就是是比较集中，离散程度较小。而5次模型的方差就比较大，同理散布比较广，离散程度较大。

所以用比较简单的模型，方差是比较小的（就像射击的时候每次的时候，每次射击的设置都集中在一个比较小的区域内）。如果用了复杂的模型，方差就很大，散布比较开。

这也是因为简单的模型受到不同训练集的影响是比较小的。

考虑不同模型的偏差：

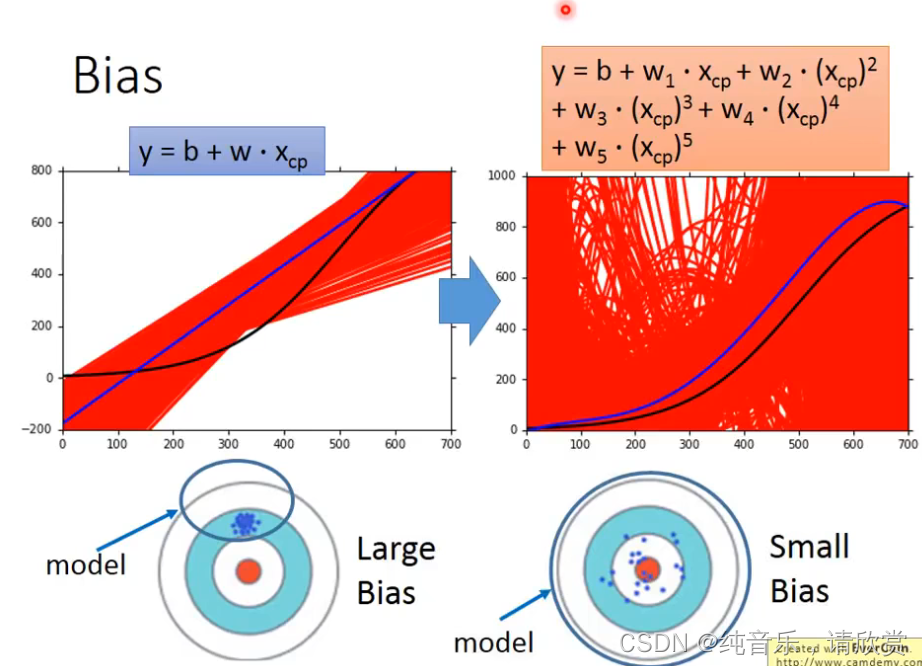
一次模型的偏差比较大，而复杂的5次模型，偏差就比较小。

直观的解释：简单的模型函数集的space比较小，所以可能space里面就没有包含靶心，肯定射不中。而复杂的模型函数集的space比较大，可能就包含的靶心，只是没有办法找到确切的靶心在哪，但足够多的，就可能得到真正的 f¯f¯。

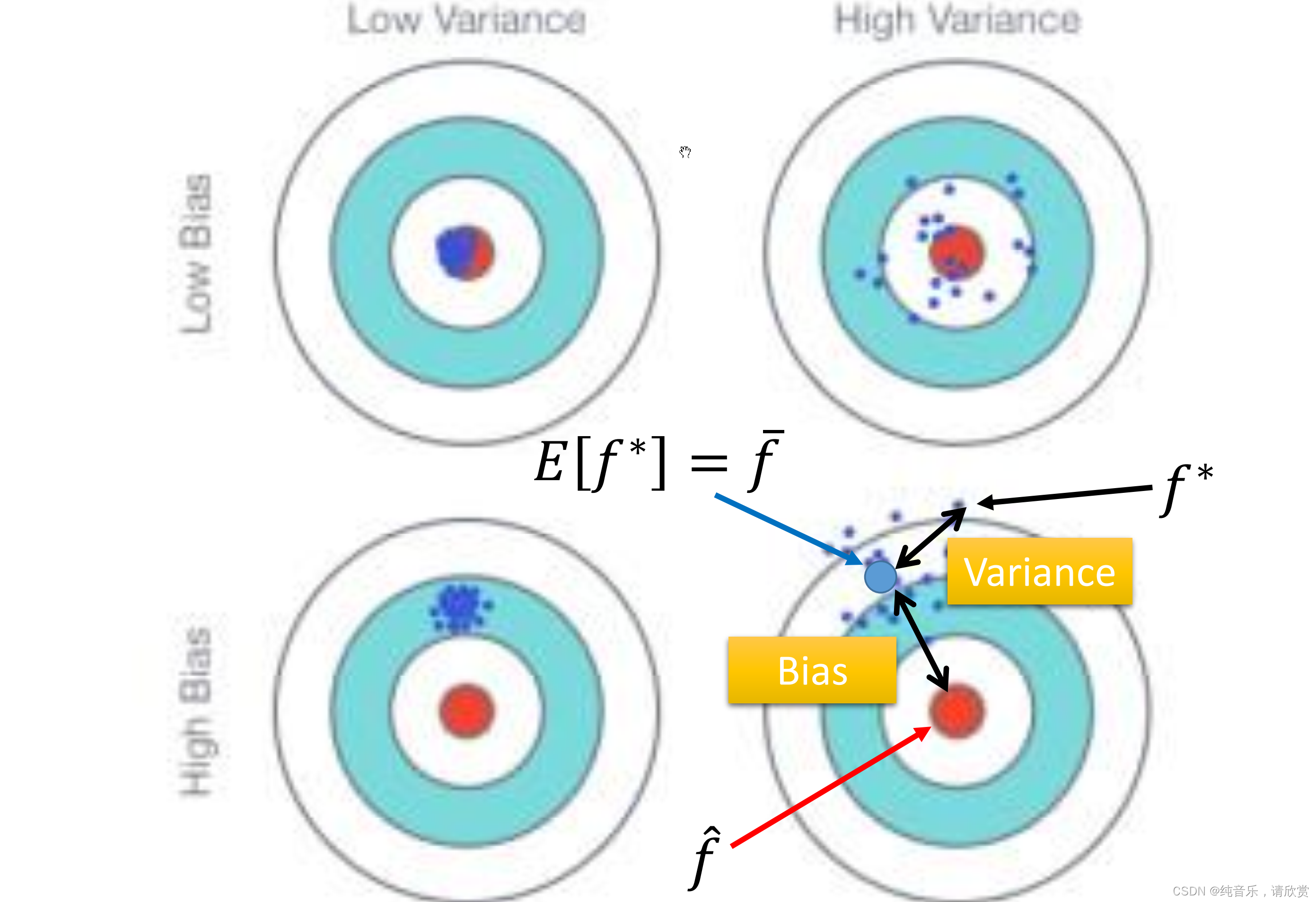
偏差v.s.方差：

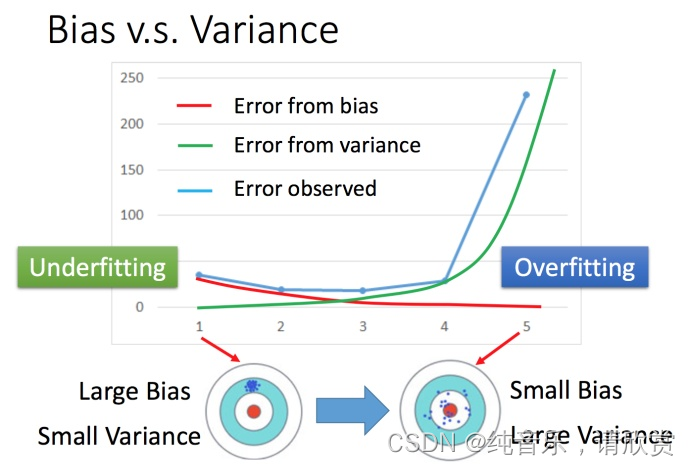
将系列02中的误差拆分为偏差和方差。简单模型（左边）是偏差比较大造成的误差，这种情况叫做欠拟合， 而复杂模型（右边）是方差过大造成的误差，这种情况叫做过拟合。

方差+偏差+数据本身的噪音

减小偏差：

怎么判断？

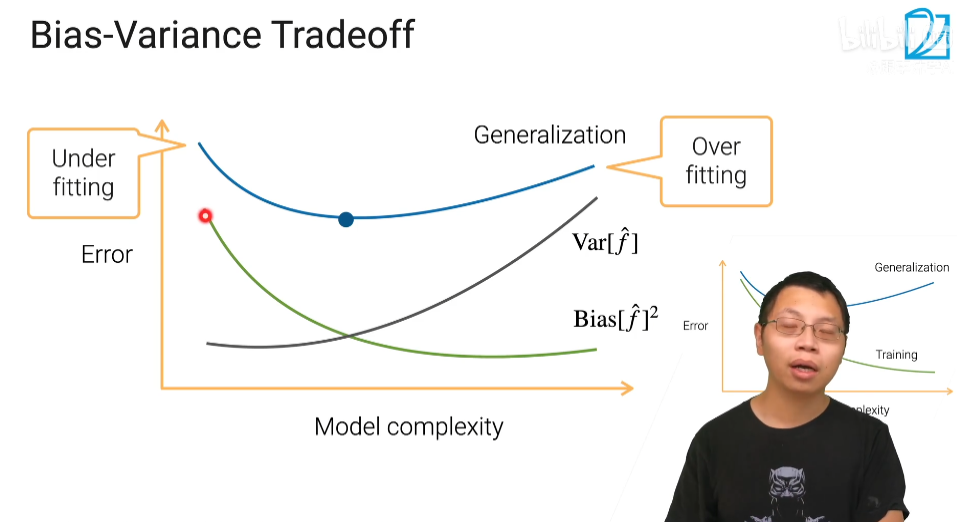
如果模型没有很好的训练训练集，就是偏差过大，也就是欠拟合 如果模型很好的训练训练集，即再训练集上得到很小的错误，但在测试集上得到大的错误，这意味着模型可能是方差比较大，就是过拟合。 对于欠拟合和过拟合，是用不同的方式来处理的

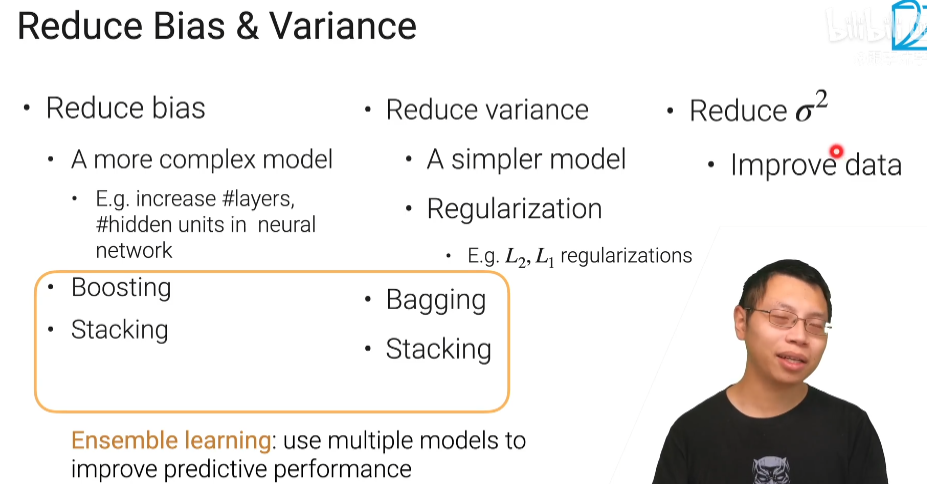
偏差大-欠拟合

此时应该重新设计模型。因为之前的函数集里面可能根本没有包含f^*可以：将更多的函数加进去，比如考虑高度重量，或者HP值等等。 或者考虑更多次幂、更复杂的模型。 如果此时强行再收集更多的data去训练，这是没有什么帮助的，因为设计的函数集本身就不好，再找更多的训练集也不会更好。

方差大-过拟合

简单粗暴的方法：更多的数据

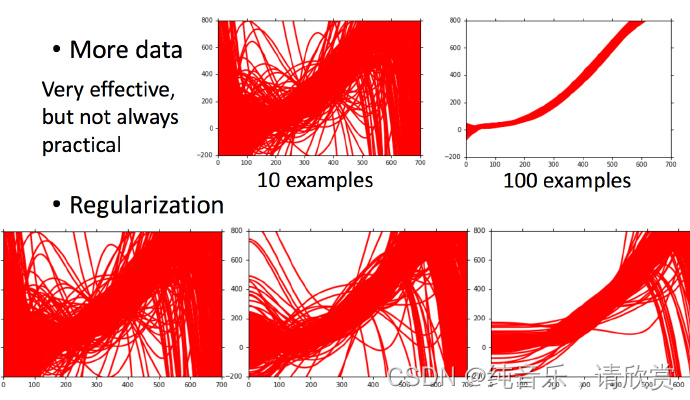
但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候，偏转角度的数据集不够，那就将正常的数据集左转15度，右转15度，类似这样的处理。

模型选择

现在在偏差和方差之间就需要一个权衡 想选择的模型，可以平衡偏差和方差产生的错误，使得总错误最小 但是下面这件事最好不要做：

用训练集训练不同的模型，然后在测试集上比较错误，模型3的错误比较小，就认为模型3好。但实际上这只是你手上的测试集，真正完整的测试集并没有。比如在已有的测试集上错误是0.5，但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。

交叉验证

图中public的测试集是已有的，private是没有的，不知道的。交叉验证 就是将训练集再分为两部分，一部分作为训练集，一部分作为验证集。用训练集训练模型，然后再验证集上比较，确实出最好的模型之后（比如模型3），再用全部的训练集训练模型3，然后再用public的测试集进行测试，此时一般得到的错误都是大一些的。不过此时会比较想再回去调一下参数，调整模型，让在public的测试集上更好，但不太推荐这样。（心里难受啊，大学数模的时候就回去调，来回痛苦折腾）

上述方法可能会担心将训练集拆分的时候分的效果比较差怎么办，可以用下面的方法。

N-折交叉验证

将训练集分成N份，比如分成3份。

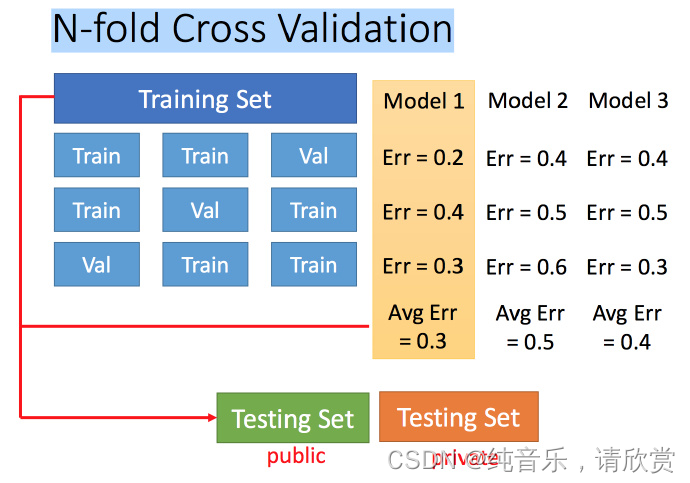
比如在三份中训练结果Average错误是模型1最好，再用全部训练集训练模型1。

正则化

参考链接

1. 正则化是一种回归的形式，它将系数估计（coefficient estimate）朝零的方向进行约束、调整或缩小。也就是说，正则化可以在学习过程中降低模型复杂度和不稳定程度，从而避免过拟合的危险。

2. L1、L2正则化（L1、L2Regularization）又叫L1范数、L2范数。目的是对损失函数（cost function）加上一个约束（也可叫惩罚项），减小其解的范围。

正则化的影响

1. 正则化后会导致参数稀疏，一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么可以对训练数据可以预测的很好，但是对测试数据就只能常可能产生过拟合了。
2. 另一个好处是参数变少可以使整个模型获得更好的可解释性。且参数越小，模型就会越简单，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。
   
   更多特征，更多input，数据量没有明显增加，仍旧导致overfitting

更多特征，但是权重 w 可能会使某些特征权值过高，仍旧导致overfitting，所以加入正则化

1. w 越小，表示 function 较平滑的， function输出值与输入值相差不大
2. 在很多应用场景中，并不是 w 越小模型越平滑越好，但是经验值告诉我们 w 越小大部分情况下都是好的。
3. b 的值接近于0 ，对曲线平滑是没有影响

概率分类模型

回归模型 vs 概率模型

假设还不了解怎么做，但之前已经学过了 regression。就把分类当作回归硬解。 举一个二分类的例子，假设输入神奇宝贝的特征 x，判断属于类别1或者类别2，把这个当作回归问题。

类别1：相当于target是 1。
类别2：相当于target是 −1。
然后训练模型：因为是个数值，如果数值比较接近 1，就当作类别1，如果数值接近 -1，就当做类别2。这样做遇到什么问题？

1. 左图：绿色是分界线，红色叉叉就是 Class2 的类别，蓝色圈圈就是 Class1 的类别。
2. 右图：紫色是分界线，红色叉叉就是 Class2 的类别，蓝色圈圈就是 Class1 的类别。训练集添加有很多的距离远大于1的数据后，分界线从绿色偏移到紫色

这样用回归的方式硬训练可能会得到紫色的这条。直观上就是将绿色的线偏移一点到紫色的时候，就能让右下角的那部分的（误差）值不是那么大了。但实际是绿色的才是比较好的，用回归硬训练并不会得到好结果。此时可以得出用回归的方式定义，对于分类问题来说是不适用的。

还有另外一个问题：比如多分类，类别1当作target1，类别2当作target2，类别3当作target3…如果这样做的话，就会认为类别2和类别3是比较接近的，认为它们是有某种关系的；认为类别1和类别2也是有某种关系的，比较接近的。但是实际上这种关系不存在，它们之间并不存在某种特殊的关系。这样是没有办法得到好的结果。

其他模型（理想替代品）：

先看二分类，将 function 中内嵌一个函数 g(x)，如果大于0，就认识是类别1，否则认为是类别2。损失函数的定义就是，如果选中某个 funciton f(x)，在训练集上预测错误的次数。当然希望错误次数越小越好。

但是这样的损失函数没办法解，这种定义没办法微分。这是有方法的，比如Perceptron（感知机），SVM等。这里先引入一个概率模型。

概率模型实现原理

盒子抽球概率举例

说明：假设两个盒子，各装了5个球，还得知随机抽一个球，抽到的是盒子1的球的概率是 2/3，是盒子2的球的概率是1/3。从盒子中蓝色球和绿色球的分配可以得到：

1. 在盒子1中随机抽一个球，是蓝色的概率为 4/5，绿的的概率为 1/5
2. 在盒子2中随机抽一个球，是蓝色的概率为 2/5，绿的的概率为 3/5
   

概率与分类的关系

将上面两个盒子换成两个类别

先验概率：

也就是在水系的神奇宝贝中随机选一只，是海龟的概率。下面将训练集中79个水系的神奇宝贝，属性Defense和SP Defense进行可视化

这里假设这79点是从高斯分布（Gaussian distribution）中采样的，现在需要从这79个点找出符合的那个高斯分布。

高斯分布：

下面简单说一下高斯分布：

最大似然估计：

应用最大似然估计计算期望和协方差：

算出之前水属性和一般属性高斯分布的期望和协方差矩阵的最大似然估计值。

分类模型

上图看出我们已经得到了需要计算的值，可以进行分类了。

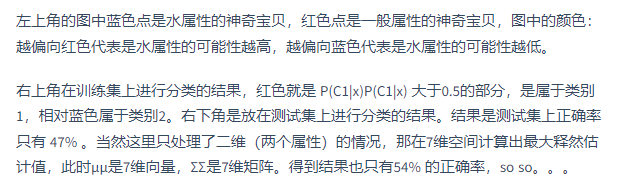
模型优化

通常来说，不会给每个高斯分布都计算出一套不同的最大似然估计，协方差矩阵是和输入feature大小的平方成正比，所以当feature很大的时候，协方差矩阵是可以增长很快的。此时考虑到model参数过多，容易Overfitting，为了有效减少参数，给描述这两个类别的高斯分布相同的协方差矩阵。

右图新的结果，分类的boundary是线性的，所以也将这种分类叫做 linear model。如果考虑所有的属性，发现正确率提高到了73%。

概率模型-建模三部曲

将上述问题简化为前几个系列说过的三大步：

实际做的就是要找一个概率分布模型，可以最大化产生data的likelihood。

为什么是高斯分布？

可能选择其他分布也会问同样的问题。。。

有一种常见的假设

假设所有的feature都是相互独立产生的，这种分类叫做 Naive Bayes Classifier（朴素贝叶斯分类器）

后验概率

求得z，然后：

logistic回归

logistic回归

Step1 逻辑回归的函数集

上一篇讲到分类问题的解决方法，推导出函数集的形式为：

将函数集可视化：
这种函数集的分类问题叫做 Logistic Regression（逻辑回归），将它和第二篇讲到的线性回归简单对比一下函数集：

Step2 定义损失函数

图中蓝色下划线实际上代表的是两个伯努利分布（0-1分布，两点分布）的 cross entropy（交叉熵）

假设有两个分布 p 和 q，如图中蓝色方框所示，这两个分布之间交叉熵的计算方式就是 H(p,q)；交叉熵代表的含义是这两个分布有多接近，如果两个分布是一模一样的话，那计算出的交叉熵就是熵

交叉熵的详细理论可以参考《Information Theory（信息论）》，具体哪本书我就不推荐了，由于学这门科目的时候用的是我们学校出版的教材。。。没有其他横向对比，不过这里用到的不复杂，一般教材都会讲到。

下面再拿逻辑回归和线性回归作比较，这次比较损失函数：

Step3 寻找最好的函数

下面用梯度下降法求：

损失函数：为什么不学线性回归用平方误差？

如果是交叉熵，距离target越远，微分值就越大，就可以做到距离target越远，更新参数越快。而平方误差在距离target很远的时候，微分值非常小，会造成移动的速度非常慢，这就是很差的效果了。

判别模型v.s. 生成模型

逻辑回归的方法称为Discriminative（判别） 方法；上一篇中用高斯来描述后验概率，称为 Generative（生成） 方法。它们的函数集都是一样的：

上图是前一篇的例子，图中画的是只考虑两个因素，如果考虑所有因素，结果是逻辑回归的效果好一些。

一个好玩的例子

上图的训练集有13组数据，类别1里面两个特征都是1，剩下的(1, 0), (0, 1), (0, 0) 都认为是类别2；然后给一个测试数据(1, 1)，它是哪个类别呢？人类来判断的话，不出意外基本都认为是类别1。下面看一下朴素贝叶斯分类器（Naive Bayes）会有什么样的结果。

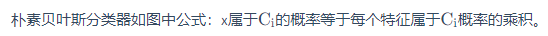
生成模型里面有种种的假设，也就是说这个model是会脑补的model

判别方法不一定比生成方法好

生成方法的优势：

训练集数据量很小的情况；因为判别方法没有做任何假设，就是看着训练集来计算，训练集数量越来越大的时候，error会越小。而生成方法会自己脑补，受到数据量的影响比较小。 对于噪声数据有更好的鲁棒性（robust）。 先验和类相关的概率可以从不同的来源估计。

比如语音识别，可能直观会认为现在的语音识别大都使用神经网络来进行处理，是判别方法，但事实上整个语音识别是 Generative 的方法，DNN只是其中的一块而已；因为还是需要算一个先验概率，就是某句话被说出来的概率，而估计某句话被说出来的概率不需要声音数据，只需要爬很多的句子，就能计算某句话出现的几率。

多类别分类

softmax

假设有3个类别，每个都有自己的weight和bias

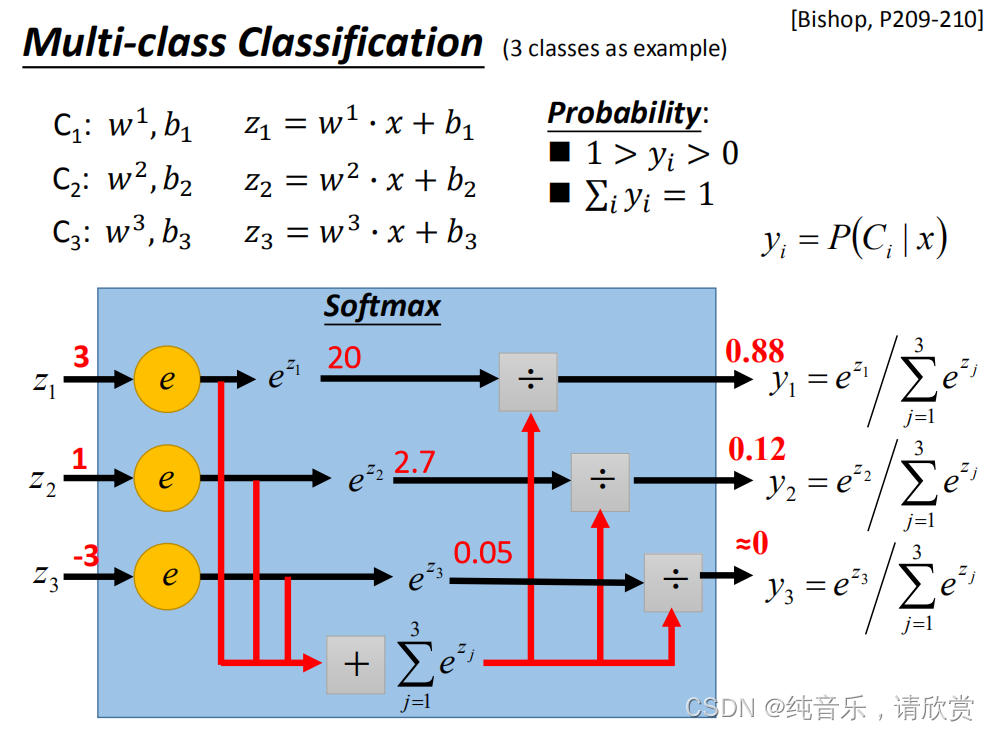
**Softmax的输出就是用来估计后验概率（Posterior Probability）。为什么会这样？**下面进行简单的说明：

为什么Softmax的输出可以用来估计后验概率？

假设有3个类别，这3个类别都是高斯分布，它们也共用同一个协方差矩阵，进行类似上一篇讲述的推导，就可以得到Softmax。

信息论学科中有一个 Maximum Entropy（最大熵）的概念，也可以推导出Softmax。简单说信息论中定义了一个最大熵。指数簇分布的最大熵等价于其指数形式的最大似然界。二项式的最大熵解等价于二项式指数形式(sigmoid)的最大似然，多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然，因此为什么用sigmoid函数，那是因为指数簇分布最大熵的特性的必然性。假设分布求解最大熵，引入拉格朗日函数，求偏导数等于0，直接求出就是sigmoid函数形式。还有很多指数簇分布都有对应的最大似然界。而且，单个指数簇分布往往表达能力有限，就引入了多个指数簇分布的混合模型，比如高斯混合，引出了EM算法。想LDA就是多项式分布的混合模型。（没懂）

定义target

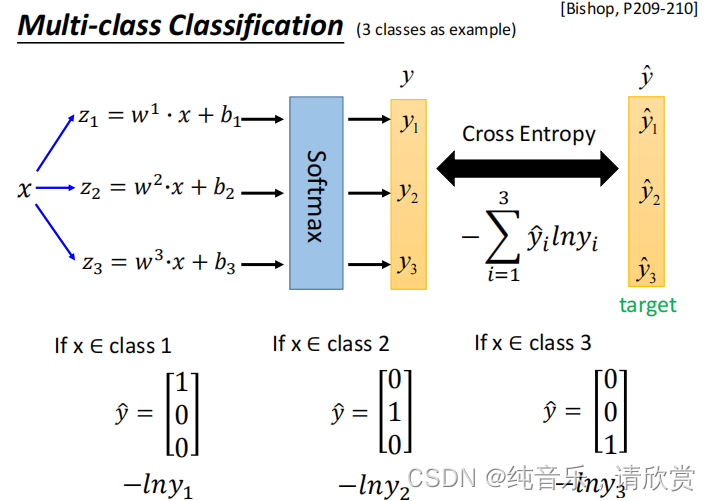
cross-entropy就是最大化似然估计

逻辑回归的限制

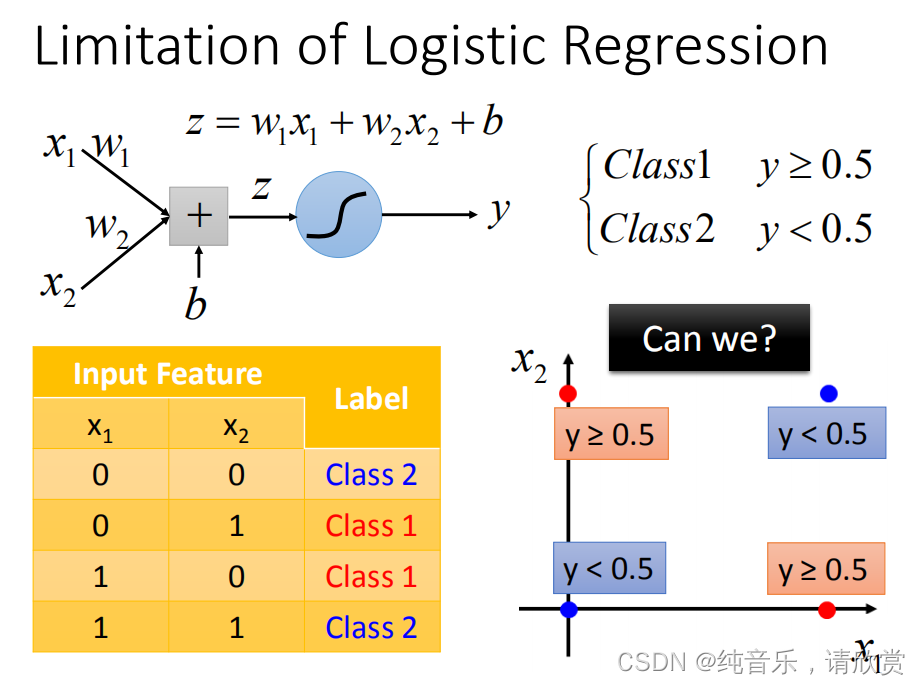
考虑上图的例子，两个类别分布在两个对角线两端，用逻辑回归可以处理吗？

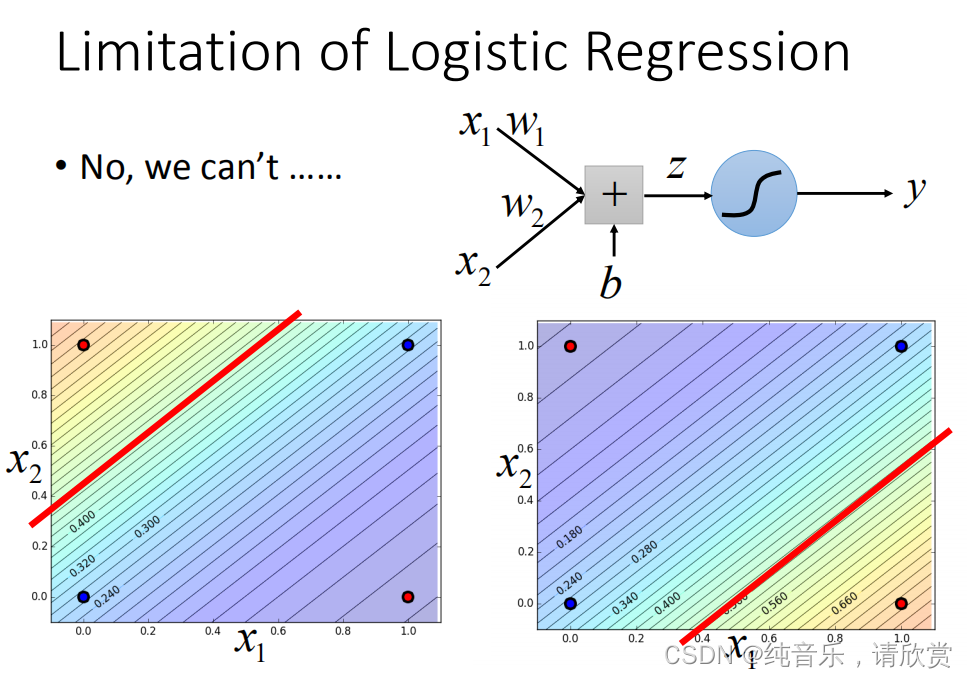
这里的逻辑回归所能做的分界线就是一条直线，没有办法将红蓝色用一条直线分开。

特征转换

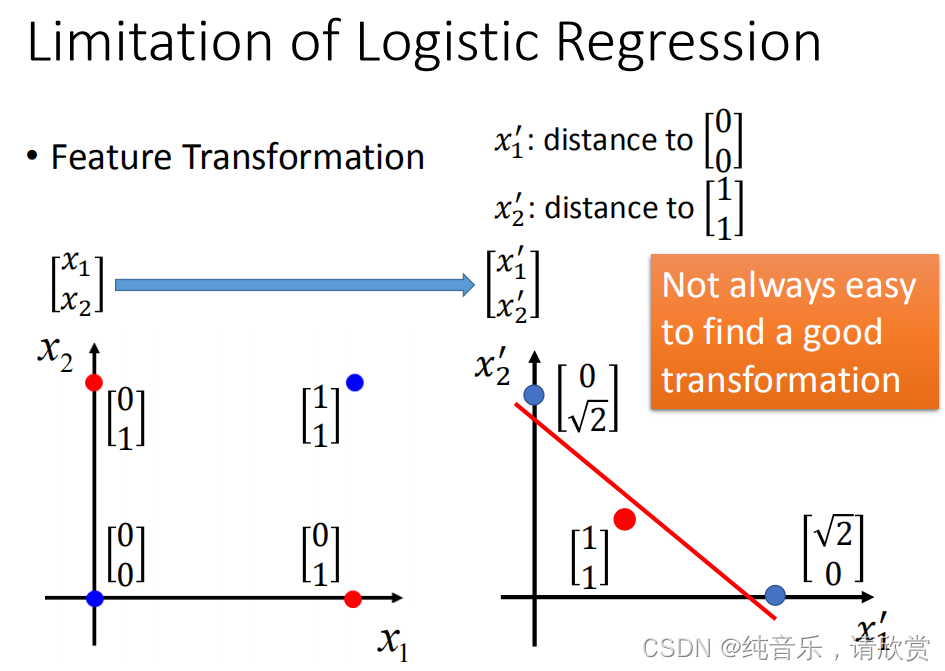
特征转换的方式很多，举例类别1转化为某个点到 (0,0)(0,0) 点的距离，类别2转化为某个点到 (1,1)(1,1) 点的距离。然后问题就转化右图，此时就可以处理了。但是实际中并不是总能轻易的找到好的特征转换的方法。

级联逻辑回归模型

可以将特征转换看做多个级联逻辑回归模型

右上角的图，可以调整参数使得得出这四种情况。同理右下角也是

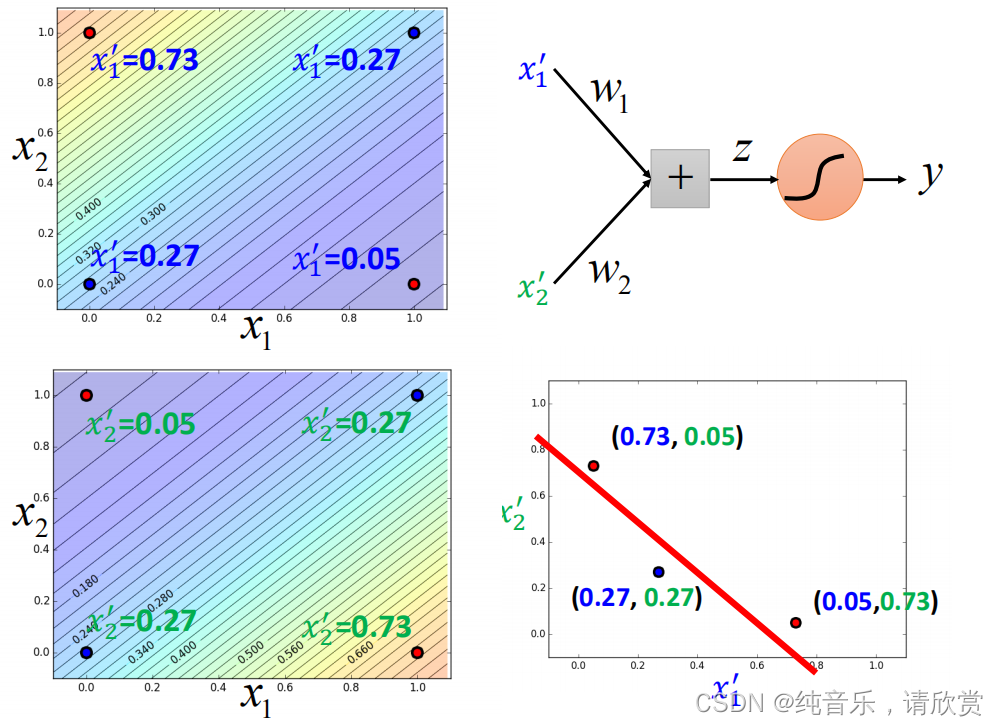
经过这样的转换之后，点就被处理为可以进行分类的结果。

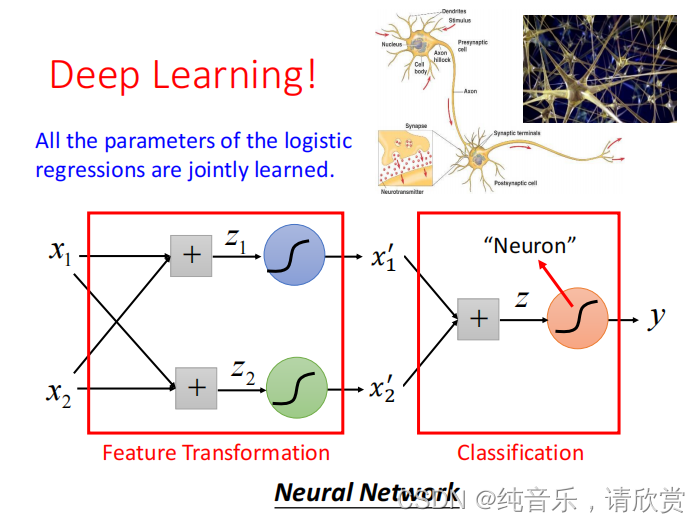
一个逻辑回归的输入可以来源于其他逻辑回归的输出，这个逻辑回归的输出也可以是其他逻辑回归的输入。把每个逻辑回归称为一个 Neuron（神经元），把这些神经元连接起来的网络，就叫做 Neural Network（神经网络）。

无监督学习-线性降维

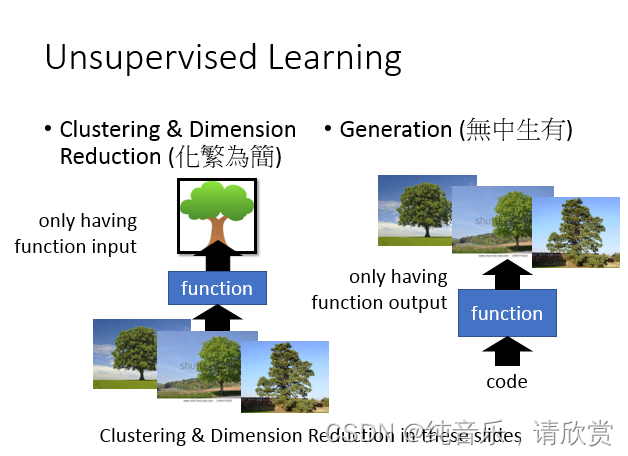
我把dimension reduction分为两种，一种做的事情叫做“化繁为简”，它可以分为两种：一种是cluster聚类，一种是dimension reduction降维。所谓的“化繁为简”的意思：现在有很多种不同的input，比如说：你现在找一个function，它可以input看起来像树的东西，output都是抽象的树，把本来比较复杂的input变成比较简单的output。那在做unsupervised learning的时候，你只会有function的其中一边。比如说：我们要找一个function要把所有的树都变成抽象的树，但是你所拥有的train data就只有一大堆的image(各种不同的image)，你不知道它的output应该是要长什么样子。

那另外一个unsupervised learning可以做Generation,也就是无中生有，我们要找一个function，你随机给这个function一个input(输入一个数字1，然后output一棵树；输入数字2，然后output另外一棵树)。在这个task里面你要找一个可以画图的function，你只有这个function的output，但是你没有这个function的input。你这只有一大堆的image，但是你不知道要输入什么样的code才会得到这些image。这张投影片我们先focus在dimension reduction这件事上，而且我们只focus在linear dimension reduction上。

聚类

那我们现在来说clustering，什么是clustering呢？clustering就是说：假设有一大堆的image，然后你就把它们分成一类一类的。之后你就可以说：这边所有的image都属于cluster1，这边都属于cluster2，这边都属于cluster3。有些不同的image用同一个cluster来表示，就可以做到“化繁为简”这件事。那这边的问题是：要到底有几个cluster，这个没有好的方法，就跟neural network要有几层一样。但是你不能太多，这张有9张image，就有9个cluster ，这样做跟没做是一样的。把全部的image放在一个cluster里，这跟没做是一样的。要怎样选择适当的cluster，这个你要empirical的来决定它

K-means

【机器学习】K-means（非常详细）
K-means 是我们最常用的基于欧式距离的聚类算法，其认为两个目标的距离越近，相似度越大。

层次聚类

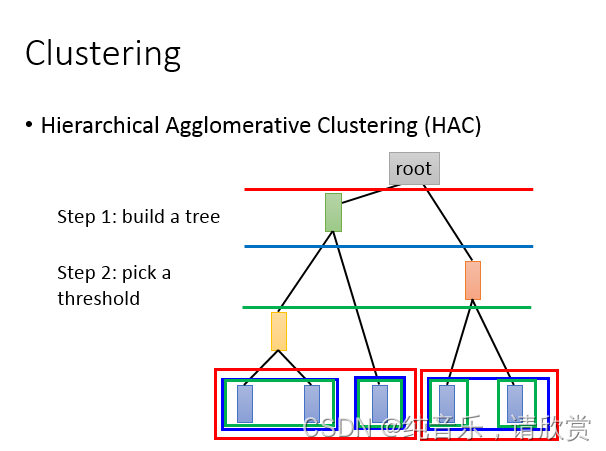
那cluster有另外一种方法叫做Hierarchical Agglomerative Clusteing(HAC),那这个方法是先建一个tree。假设你现在有5个example，你想要把它做cluster，那你先做一个tree structure，咋样来建这个tree structure呢？你把这5个example两两去算它的相似度，然后挑最相似的那个pair出来。假设最相似的那个pair是第一个example和第二个example merge起来再平均，得到一个新的vector，这个vector代表第一个和第二个example。现在只剩下四笔data了，然后两两再算相似度，发现说最后两笔是最像的，再把他们merge average起来。得到另外一笔data。现在只剩下三笔data了，然后两两算他们的similarity，发现黄色这个和中间这个最像，然后再把他们平均起来，最后发现只剩红色跟绿色，在把它们平均起来，得到这个tree 的root。你就根据这五笔data他们之间的相似度，就建立出一个tree structure，这只是建立一个tree structure，这个tree structure告诉我们说：哪些example是比较像的。比较早分枝代表比较不像的。

接下来你要做clustering，你要决定在这个tree structure上面切一刀(切在图上蓝色的线)，你如果切这个地方的时候，那你就把你的五笔data变成是三个cluster。如果你这一刀切在红色的那部分，就变成了二个cluster，如果你这一刀切在绿色这一部分，就变成了四个cluster。这个就是HAC的做法

HAC跟刚才K-means最大的差别就是：你如果决定你的cluster的数目，在k-means里面你要决定K value是多少，有时候你不知道有多少cluster不容易想，你可以换成HAC，好处就是你现在不决定有多少cluster，而是决定你要切在这个 tree structure的哪里。

Distributed Representation

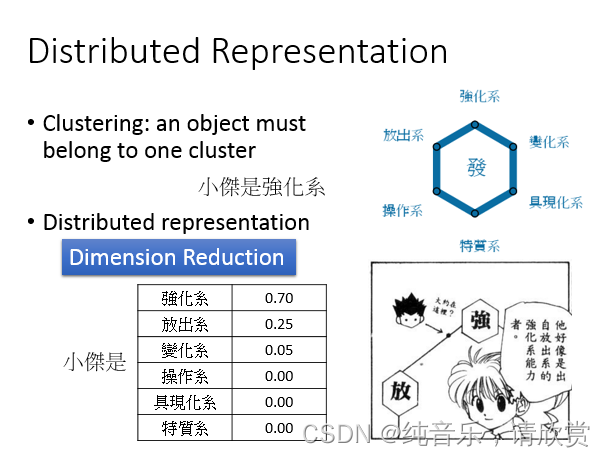
光只做cluster是非常卡的，在做cluster的时候，我们就是"以偏概全"这个就好像说：“念能力”有分成六大类，每一个人都要被assign成这其中的一类。要咋样决定它是属于哪一类呢？拿一杯水看看它有什么反应，就assign成哪一类。比如说：水满出来了就是强化系，所以小傑是强化系。这样子把每一个人都assign某一个系是不够的，太过粗糙的。像bisiji就有说：小傑其实是接近放出系的强化系能力的念能力者。如果你只是说它是强化系的，这是loss掉很多information的，你应该这样表示小傑，应该说：强化系是0.7，放出系是0.25，强化系是跟变化系是比较接近的，所以有强化系就有一部分的变化系的能力，其他系的能力为0。所以你应该要用一个vector来表示你的xx，那这个vector每一个dimension就代表了某一种特值，那这件事就叫做：distributed representation。

如果原来你的x是一个非常high dimension的东西，比如说image，你现在用它的特值来描述，它就会从比较高维的空间变成比较低维的空间。那这件事情就被叫做：dimension reduction。这是一样的事情，只是不同的称呼而已。

降维

降维样例

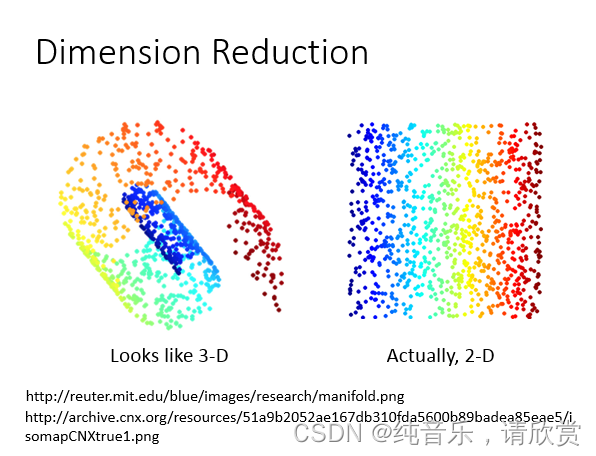
那从另外一个角度来看：为什么dimension reduction可能是有用的。举例来说：假设你的data分布是这样的(在3D里面像螺旋的样子)，但是用3D空间来描述这些data其实是很浪费的，其实你从资源就可以说：你把这个类似地毯卷起来的东西把它摊开就变成这样(右边的图)。所以你只需要在2D的空间就可以描述这个3D的information，你根本不需要把这个问题放到这个3D来解，这是把问题复杂化，其实你可以在2D就可以做这个task

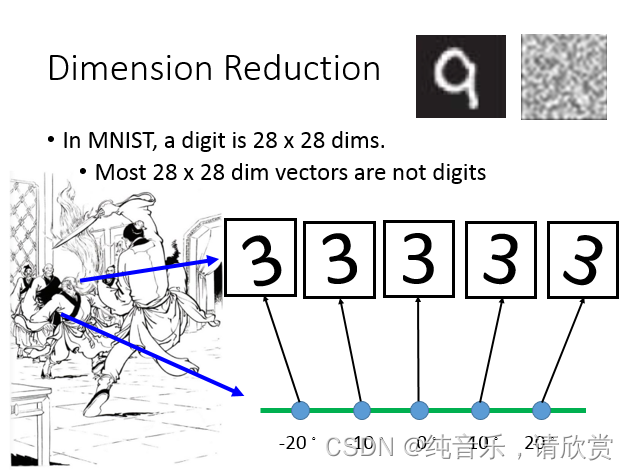
我们来举一个具体的例子：比如说我们考虑MNIST，在MNIST里面，每一个input digit都是用28*28dimension来描述它。但是多数28 *28dimension的vector你把它转成一个image看起来不像一个数字。你random sample一个28 *28vector转成一个image，可以是这样的(数字旁边的图)，它看起来根本就不不像数字。 **所以在这28 *28维空间里面 。digit这个vector其实是很少的，所以你要描述一个digit，你根本就不需要用到28 28维，你要描述一个digit，你要的dimension远比28 28维少。

我们举一个很极端的例子：比如说这里有一堆3，这堆3如果你是从pixel来看待的话，你要用28*28维来描述一个image，然后实际上这些3只需要一个维度就可以来表示了。为什么呢？因为这些3就只是说：把原来的3放在这就是中间这张image，右转10度就是这张，右转2度变它，左转10、20度。所以你唯一要记录的只有今天这张image它是左转多少度右转多少度，你就可以知道说它在维的空间里面应该长什么样子。你只需要抓重这个重点(角度的变化)，你就可以知道28维空间中的变化，所以你只需要一维就可以描述这些image

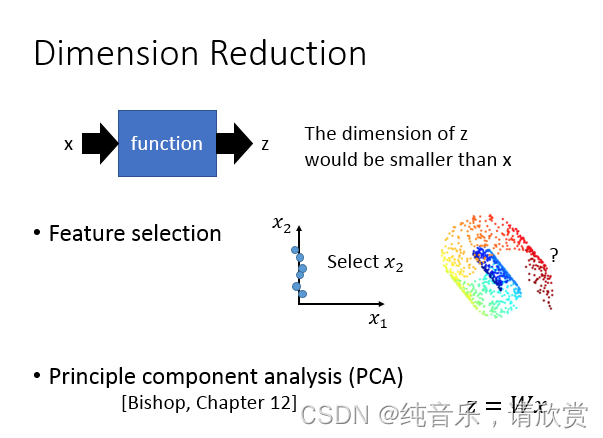
那怎么做dimension reduction呢?在做dimension reduction的时候，我们要做的事情就是找一个function，这个function的input是一个vector x，output是另外一个vector z。但是因为是dimension reduction，所以你output这个vector z这个dimension要比input这个x还要小，这样才是在做dimension reduction。

特征选择

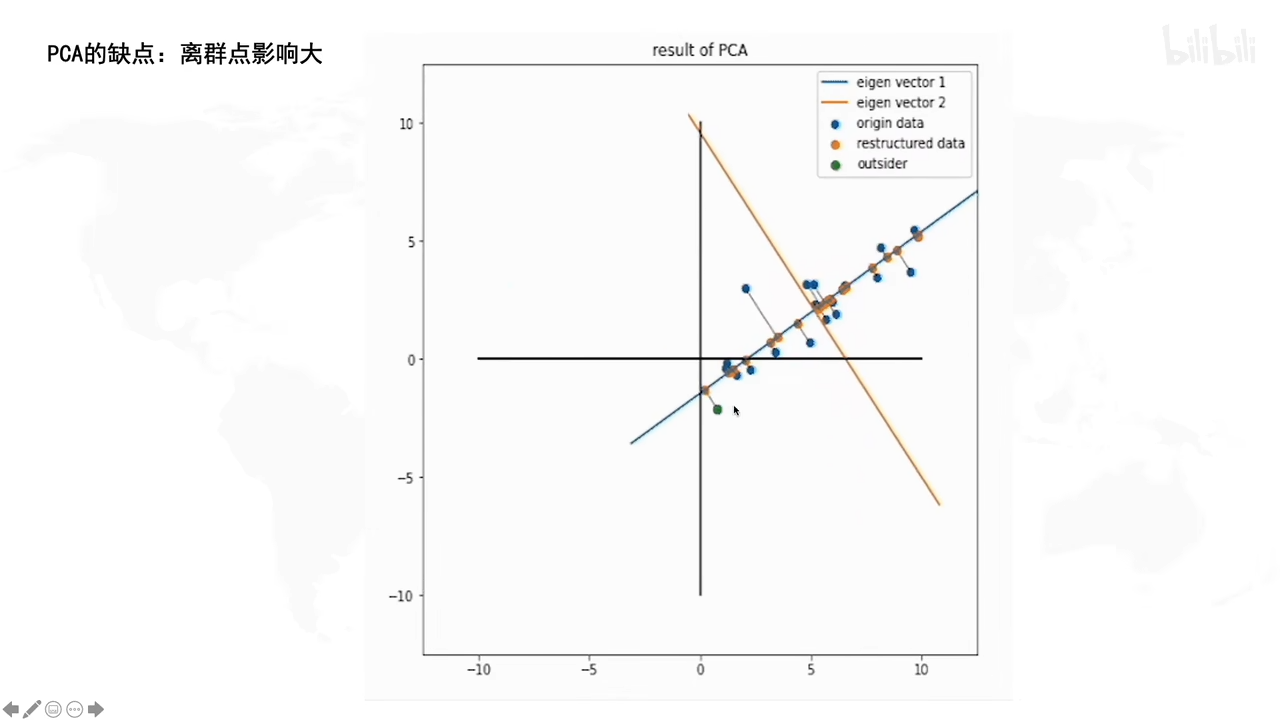
主成分分析

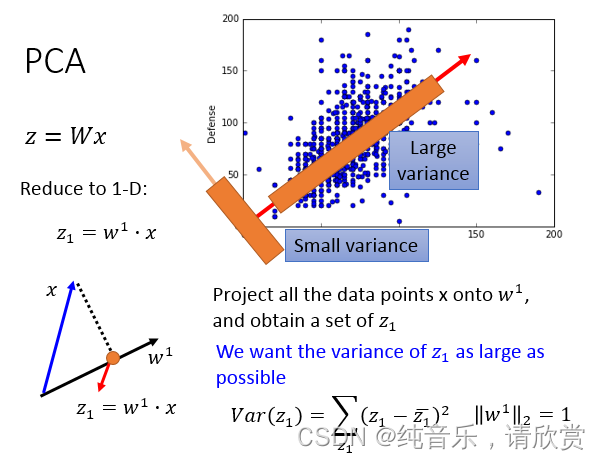
另外一个常见的方法叫做Principe component abalysis(PCA), PCA做的事情就是：这个function是一个很简单的linear function，这个input x跟这个output z之间的关系就是一个linear transform，你把这个x乘上一个matrix w，你就得到它的output z。 现在要做的事情就是:根据一大堆的x(我们现在不知道z长什么样子)我们要把w找出来

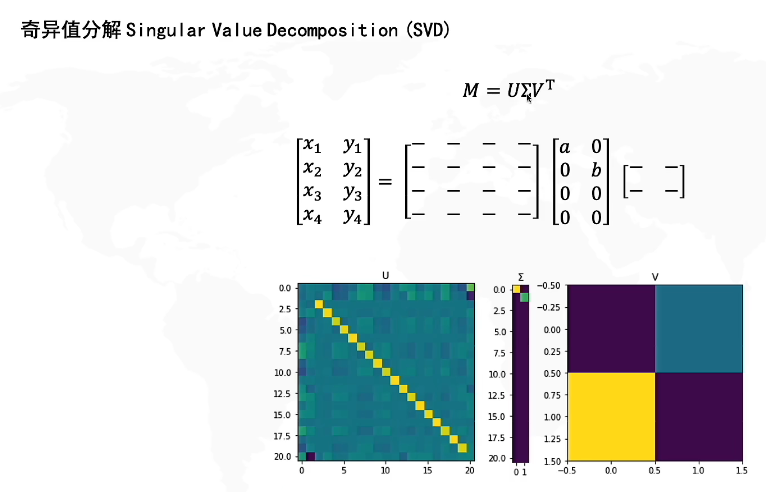
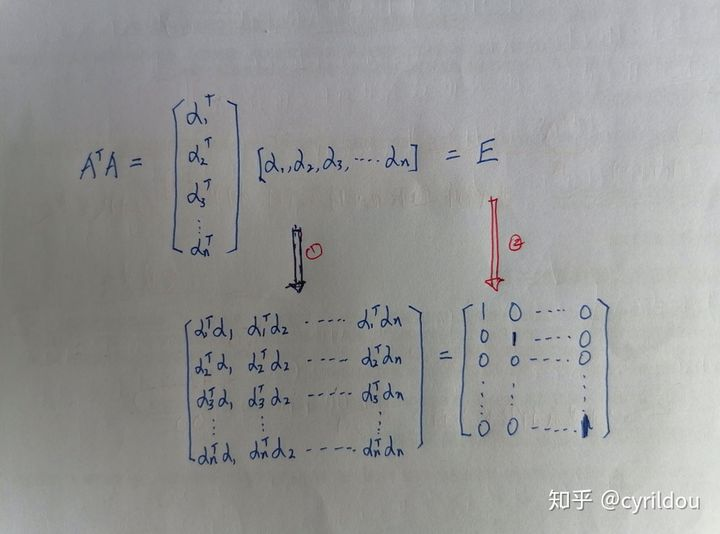
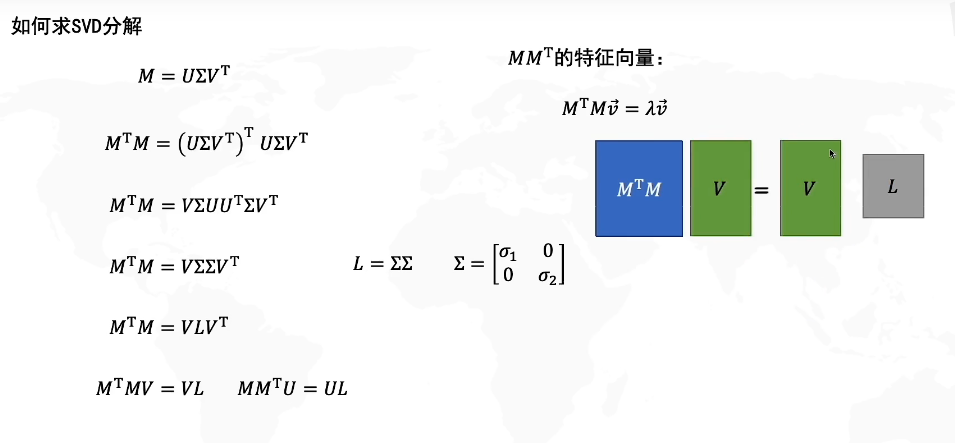
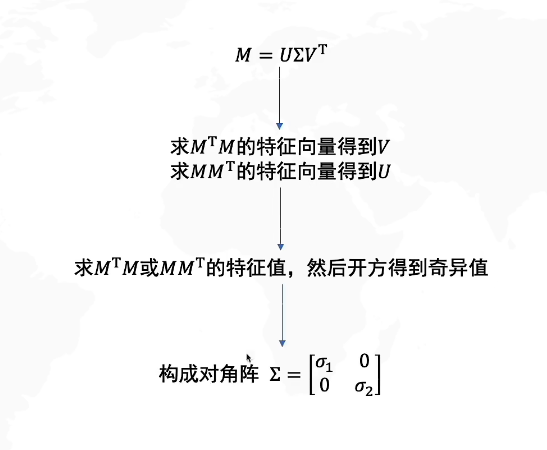
前置知识：奇异值分解

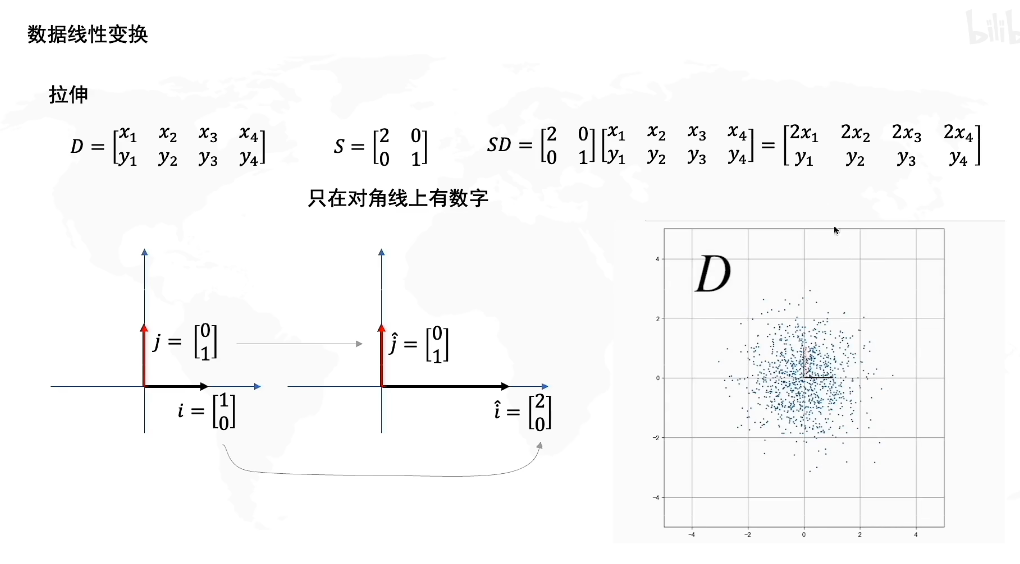
先看一下数据线性变换：

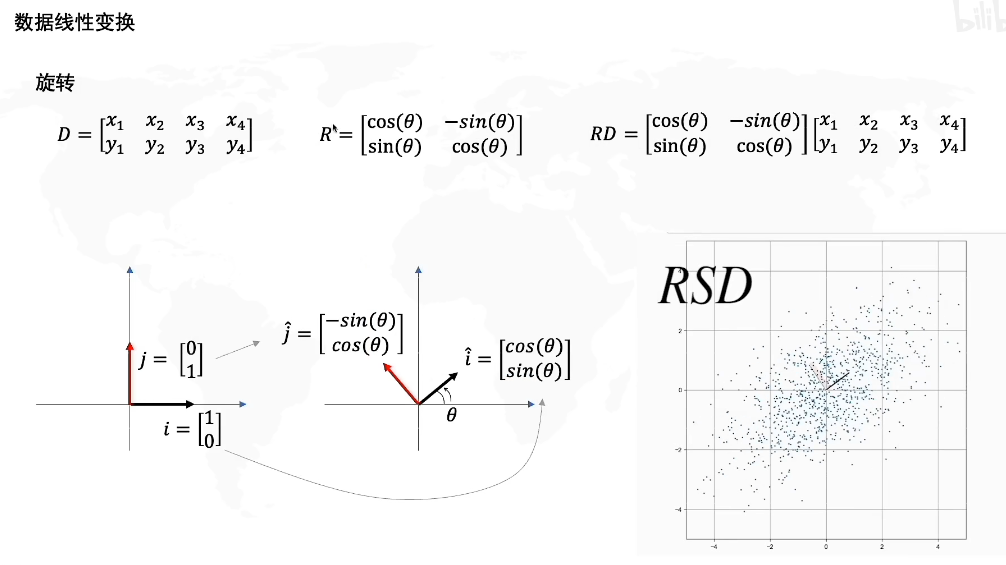
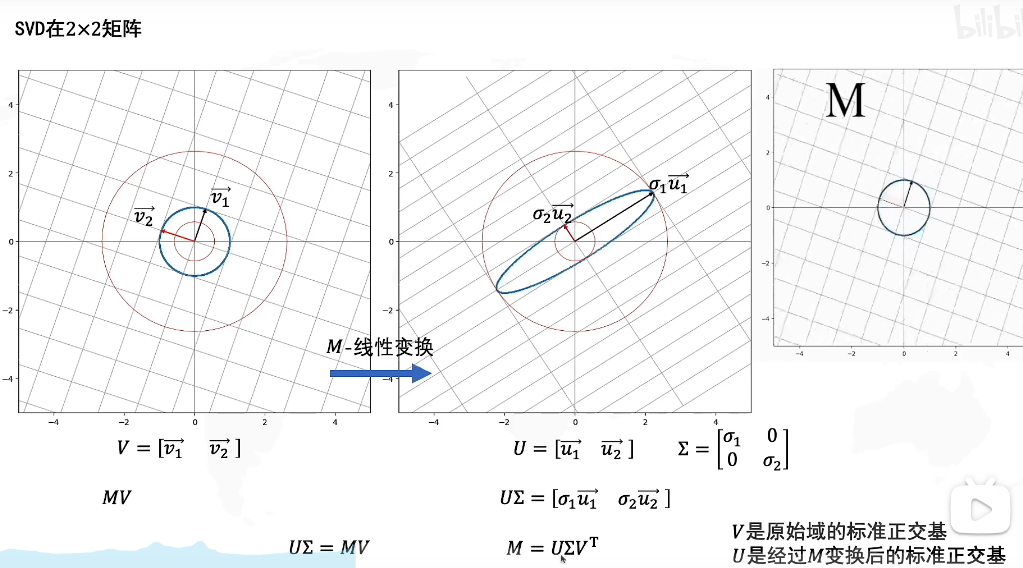
SVD在2*2矩阵：

V是正交矩阵的话，代表的意义就是旋转

补充：正交矩阵

如果是对角矩阵，也就是只有对角线上有值，那就是拉伸

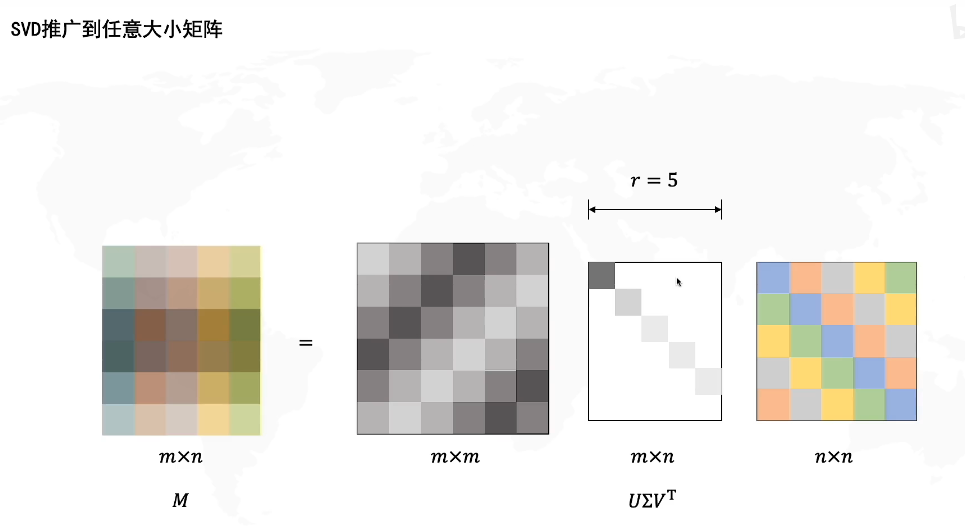
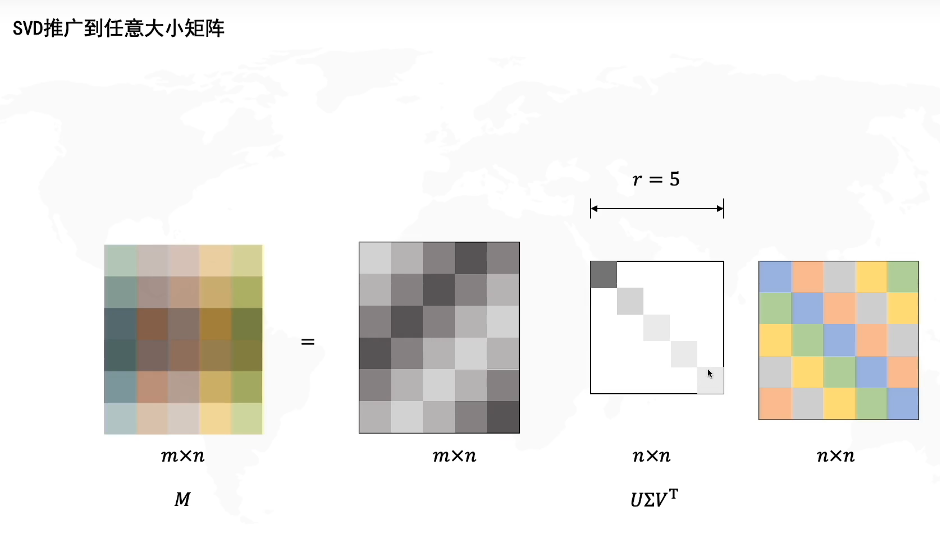
取前几个奇异值：

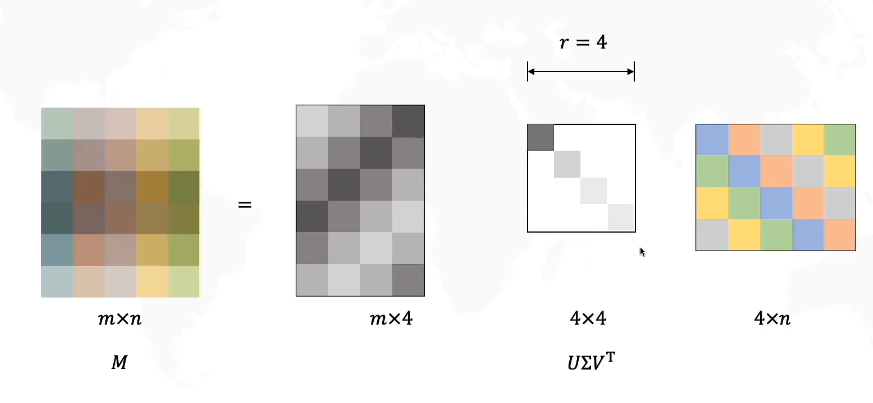
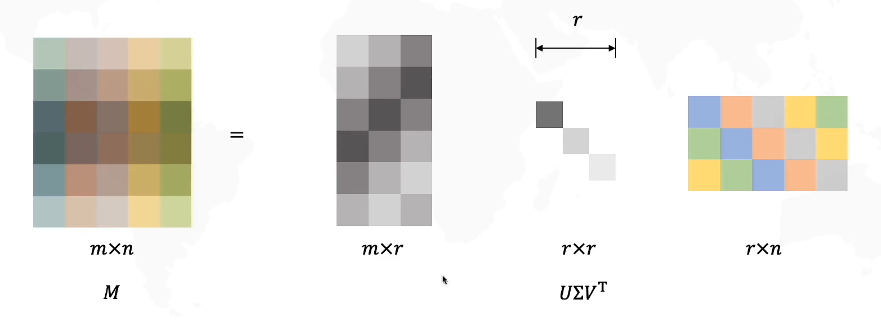
这样做有什么意义呢？

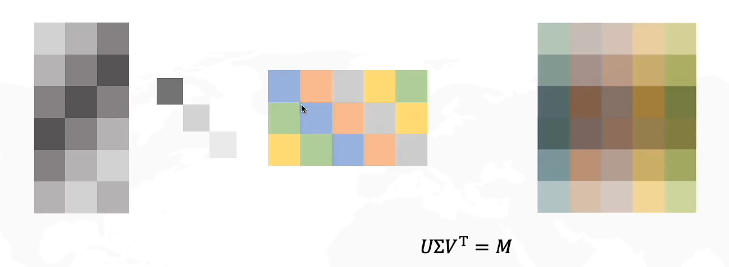
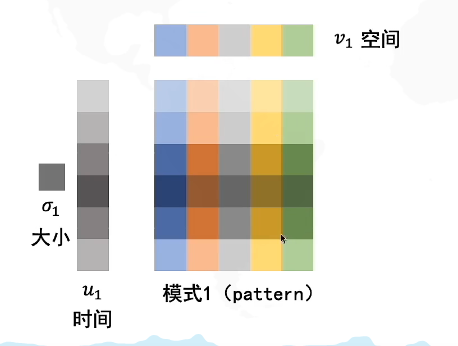
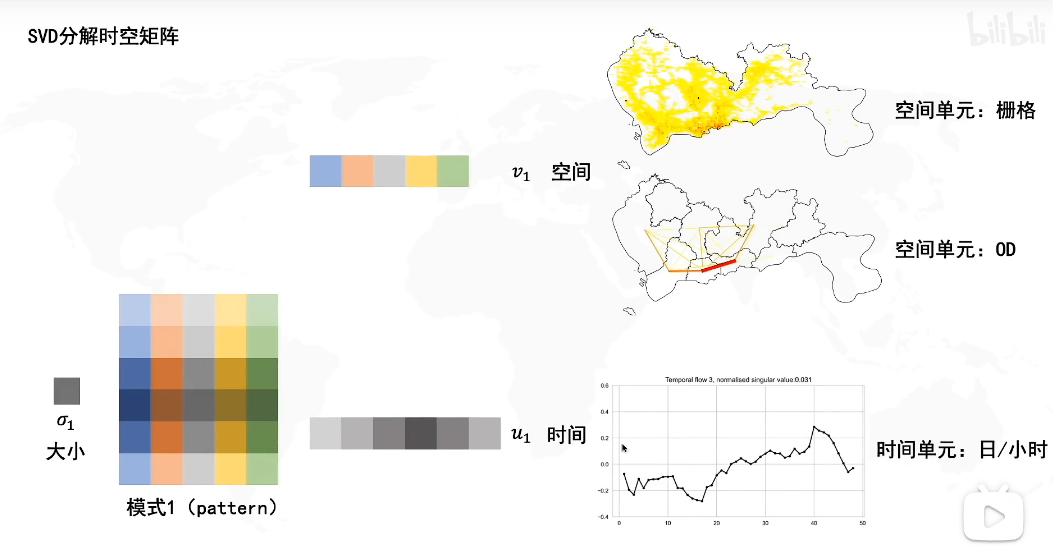
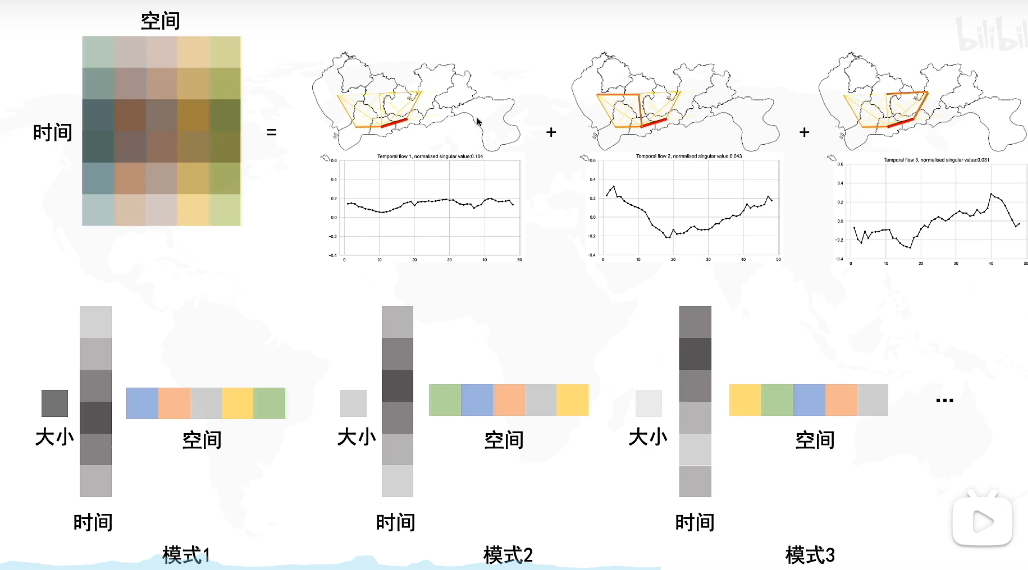
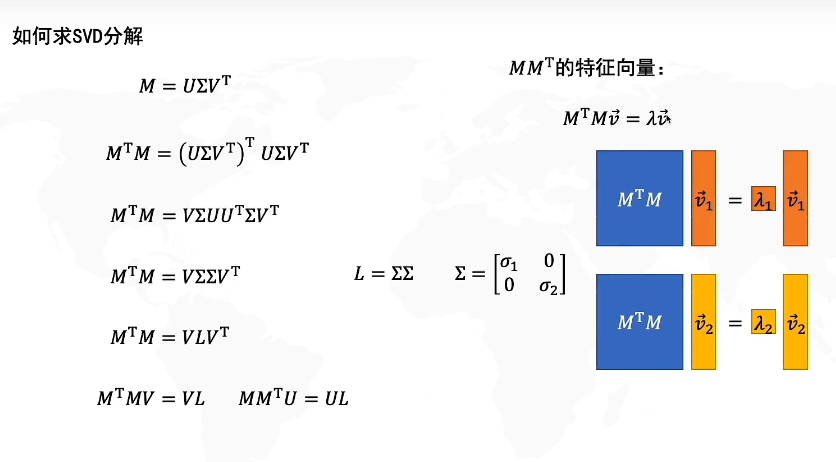
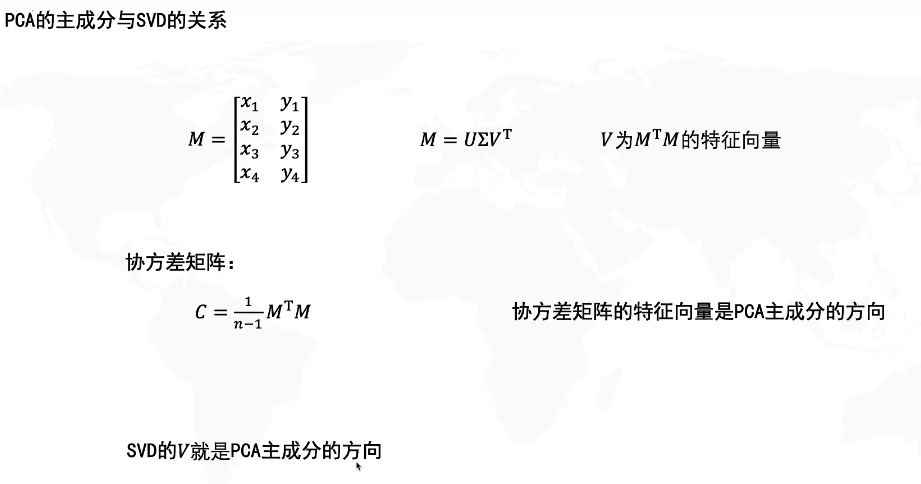
什么是主成分分析PCA

假设要保存二维的信息，由于降维考虑，期望只存储一个维度的信息（为了减少存储的信息量）

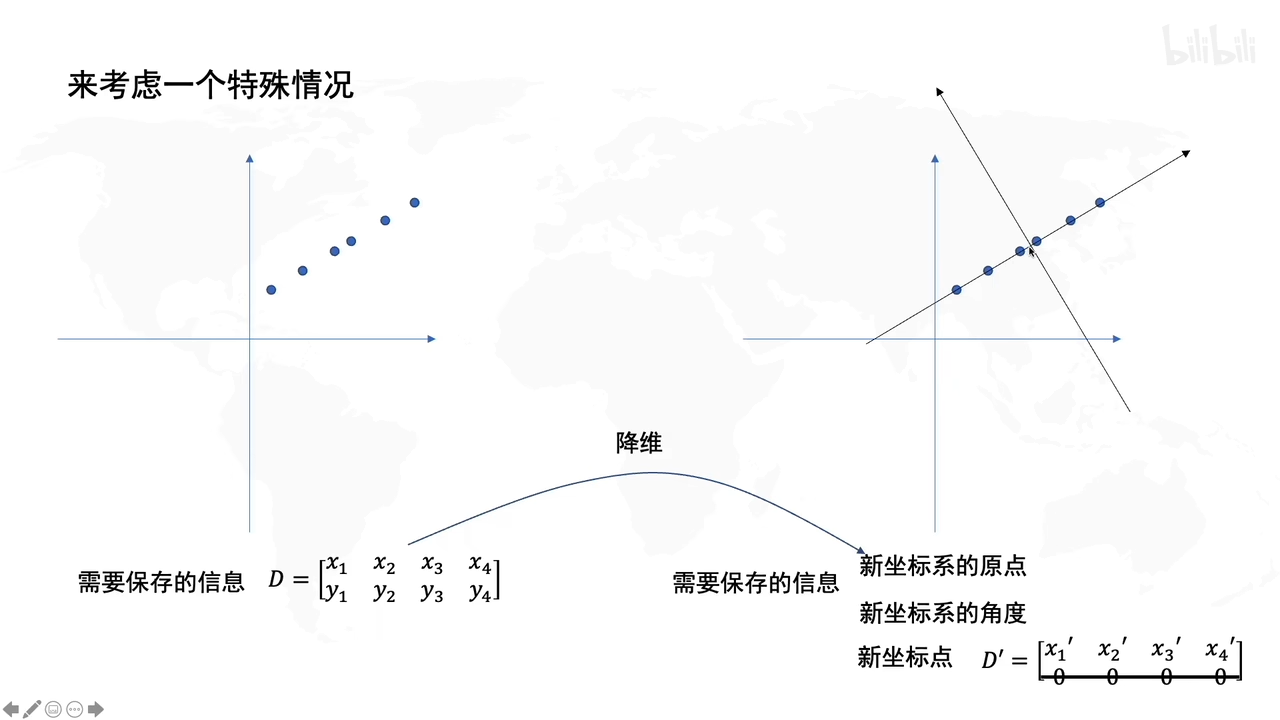
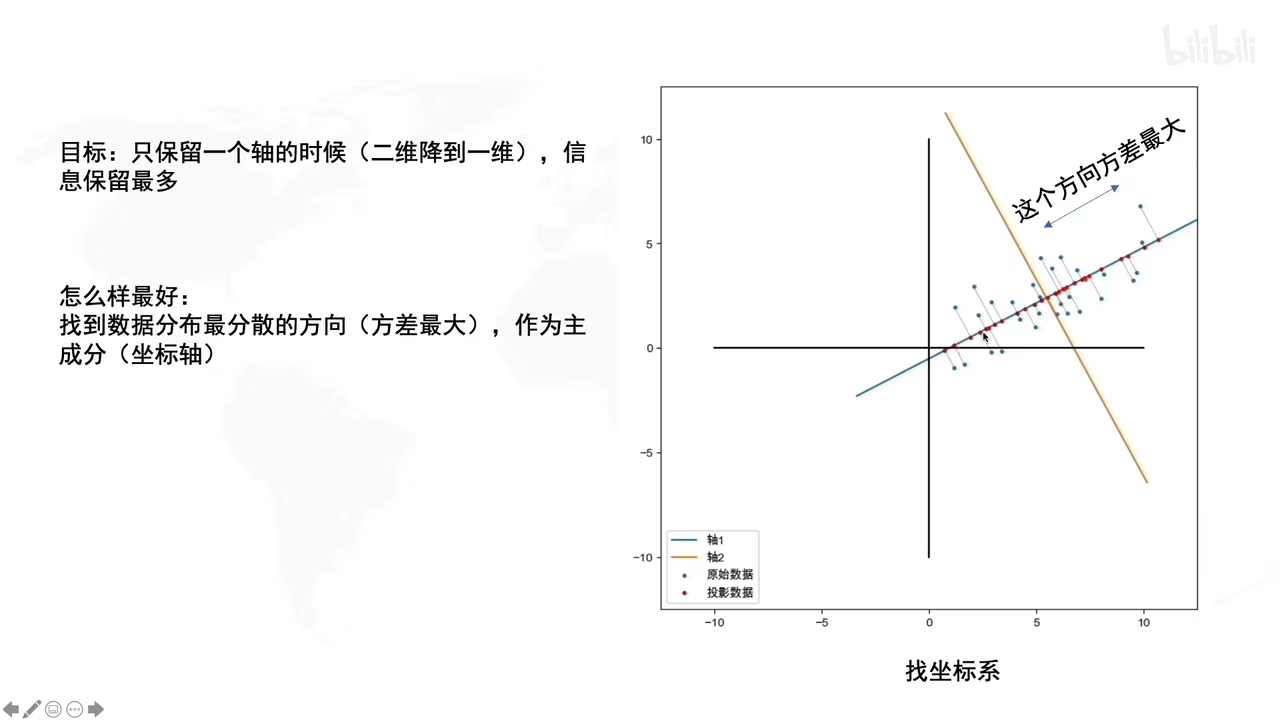
PCA是找到一个新的坐标系去存储一维信息。这个坐标系的原点落在数据的中心，坐标系的方向是往数据分布的方向上走，这样子就是降维了。

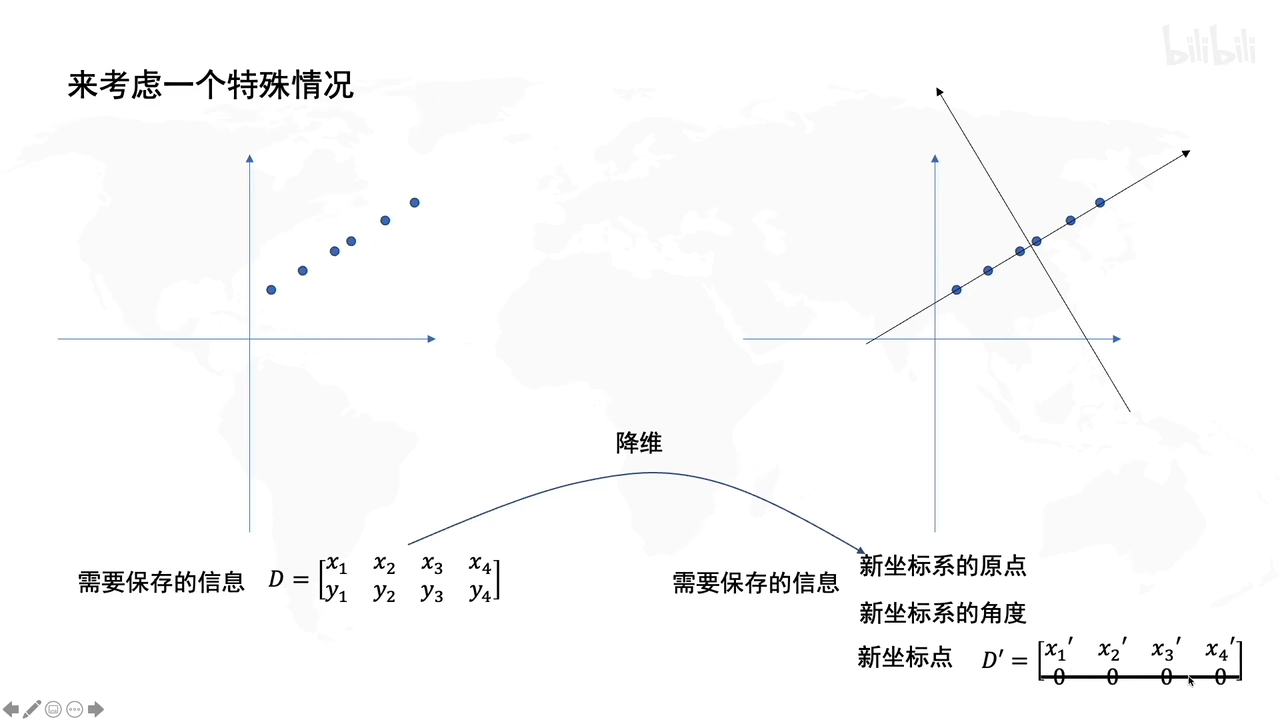
原始的数据点是蓝色的点，红色的点是蓝色的点投影到轴上的。这样通过某一些角度，只保留一维信息就能存储二维的信息量了（当然也存在信息损失，但此时目的是为了降维信息的情况下另信息损失度最小）

在上图就是很好的显示了，因为坐标点投影得比较分散，易于显示。

若发现投影后数据集中在一个点红色的斑点的话，说明没有保存多少信息，因为信息重合混淆了，数据不能很好地在新坐标系下区分开。

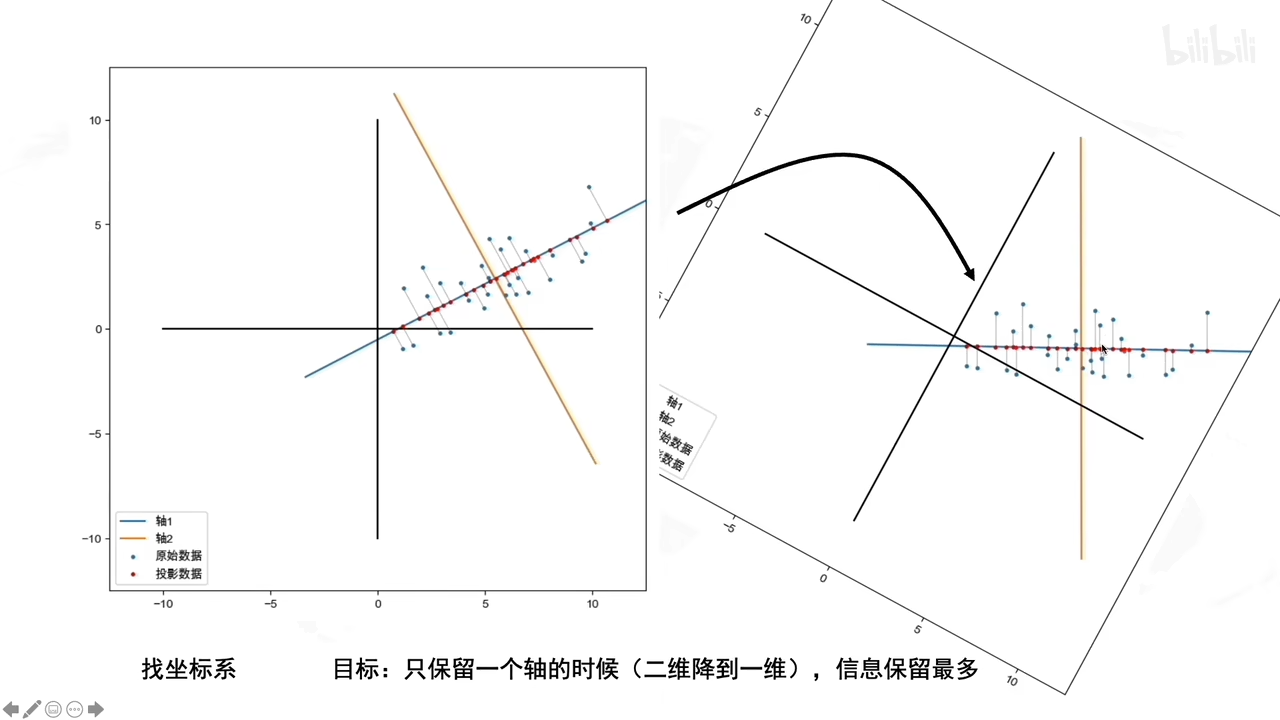
那怎么样才算好的坐标系呢？

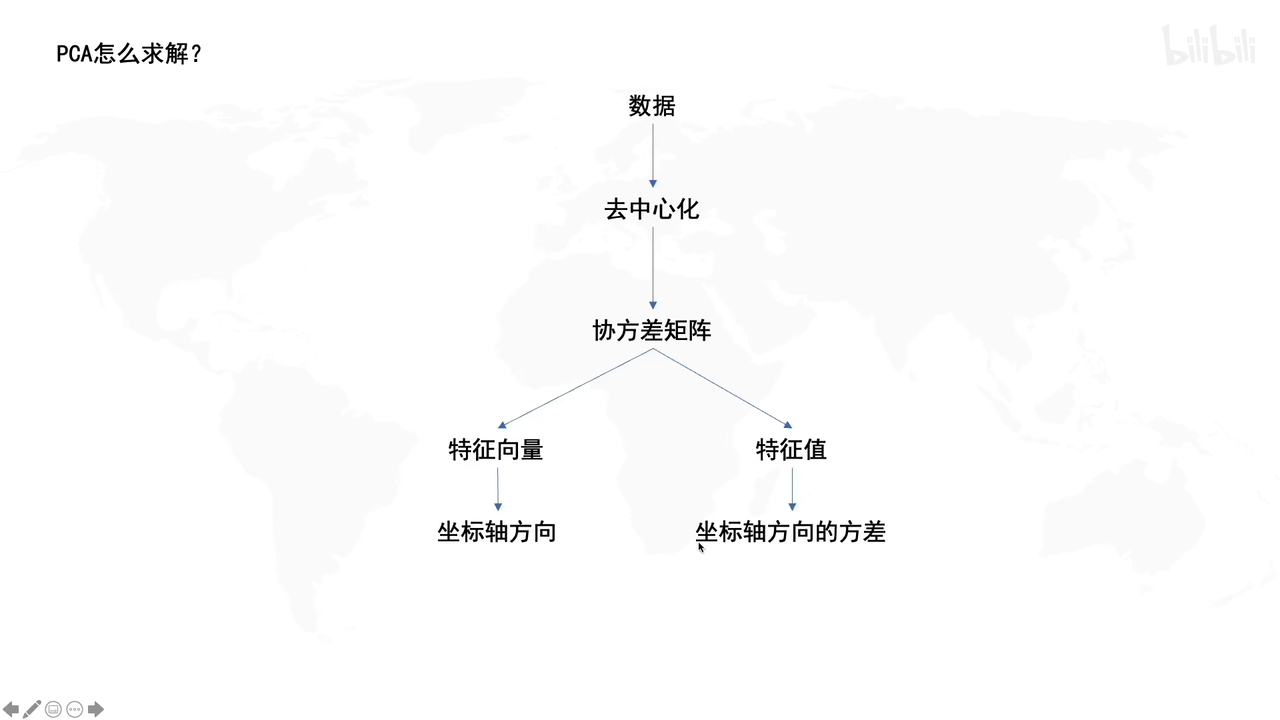
具体步骤：

若没有去中心化直接找坐标系，就会：发现不了一个好的方向让数据投影在新坐标系上分散开来。 （接下来求协方差矩阵时不会被数据数值影响）
数学思想：

利用线代里的线性变化

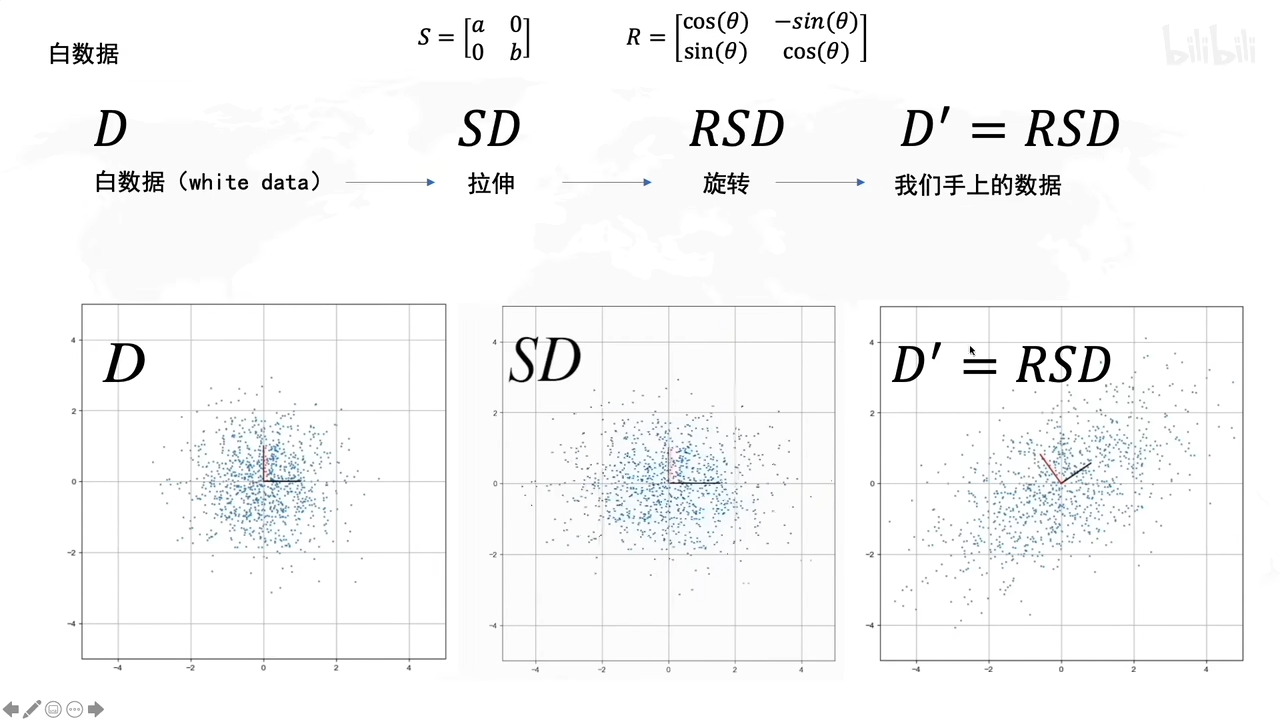
拉伸操作：

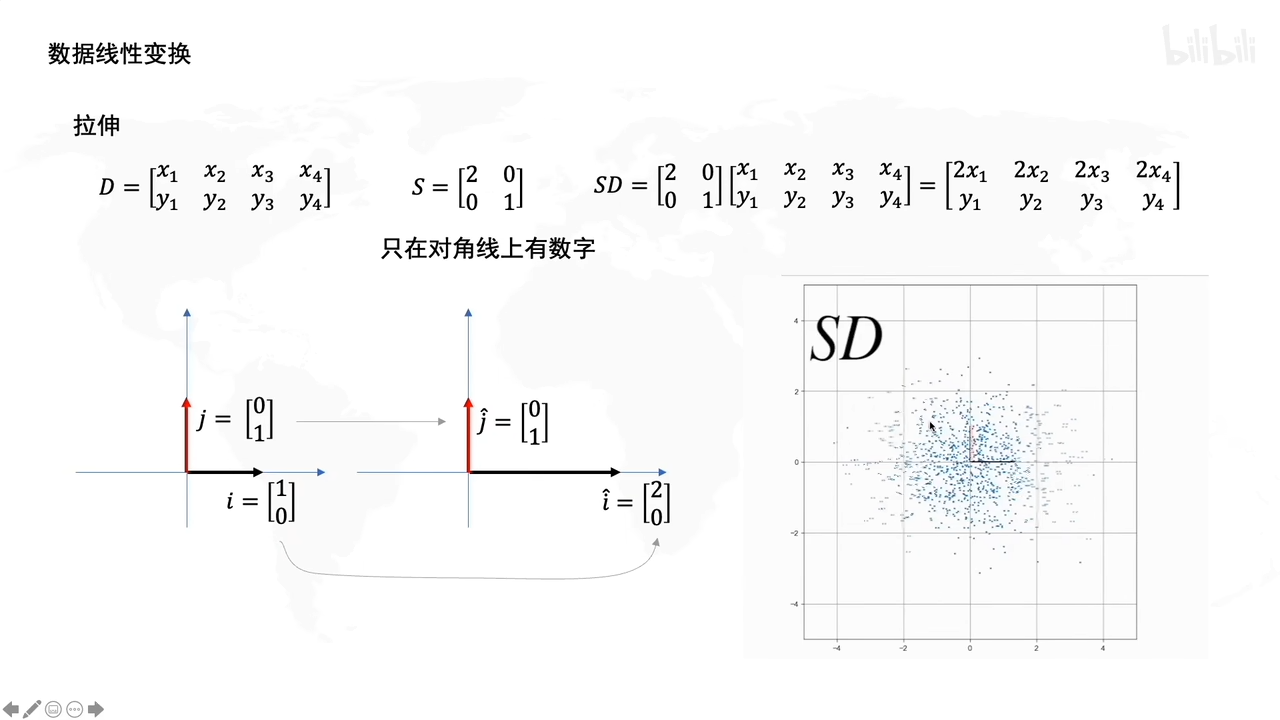
比如这里，D是一个数据集，S表示拉伸的矩阵（为了实现数据拉伸的）

S左乘D之后，相当于把D上的数据点拉伸了。

旋转操作：

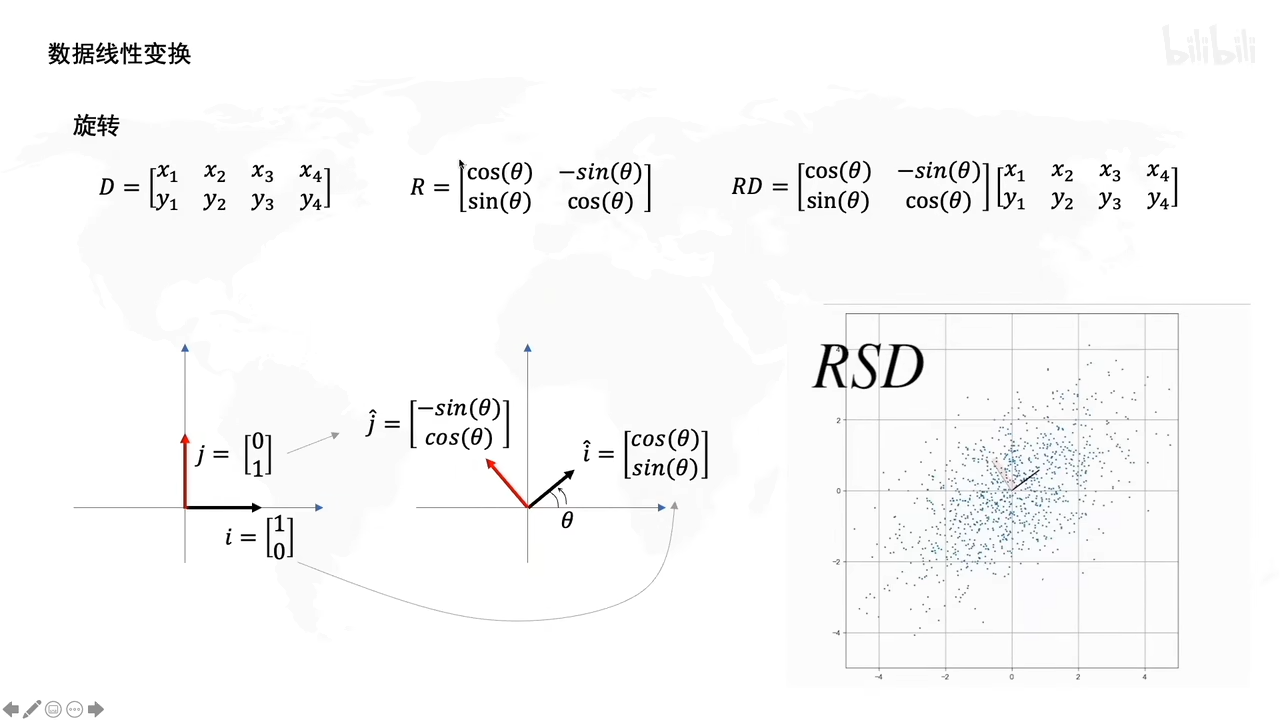
R就是个旋转矩阵，R左乘D后，让D旋转了某个角度。

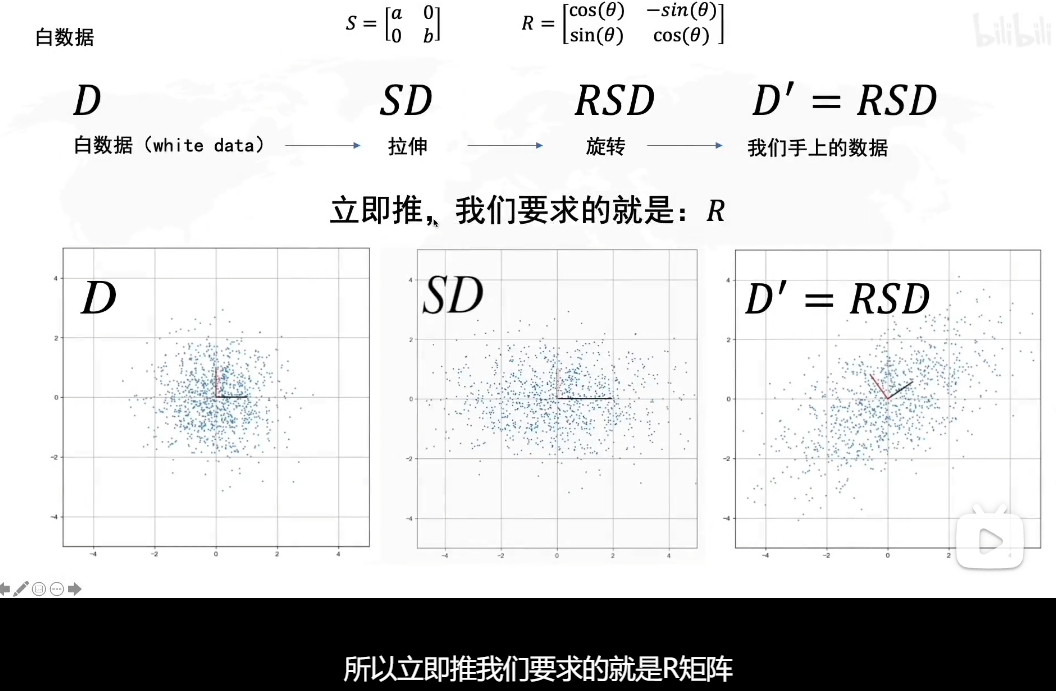
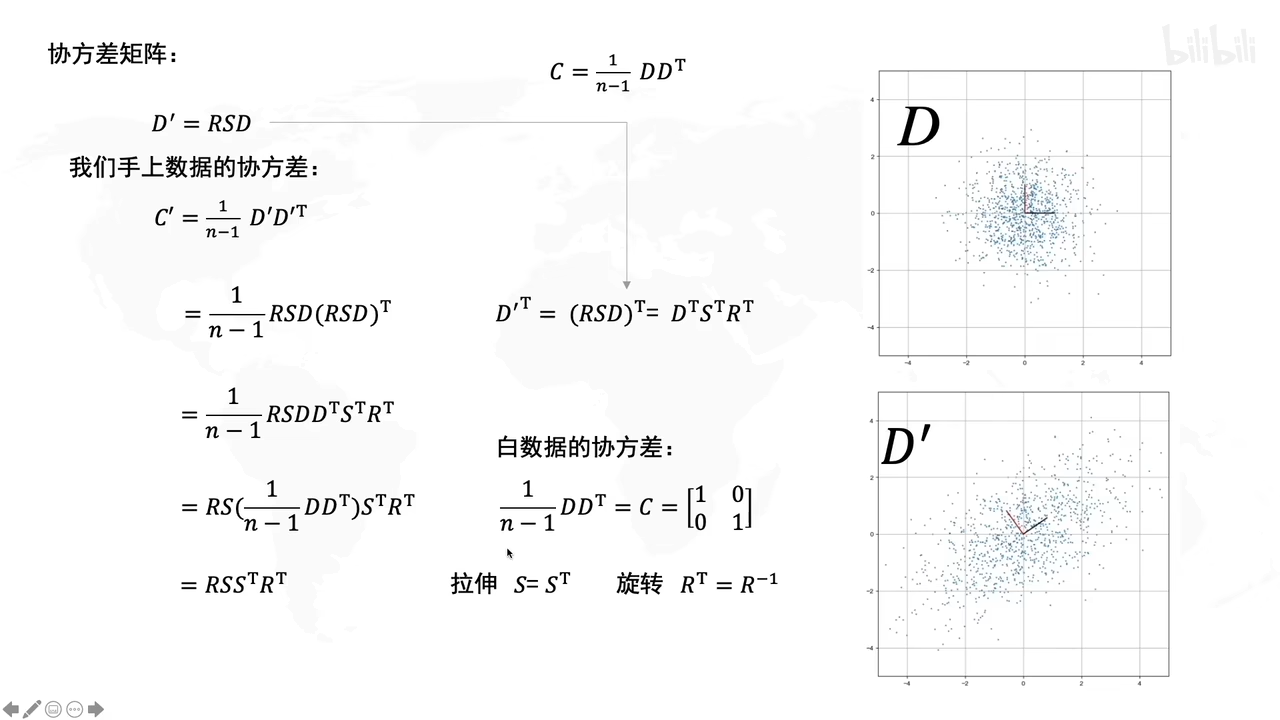
白数据的处理：

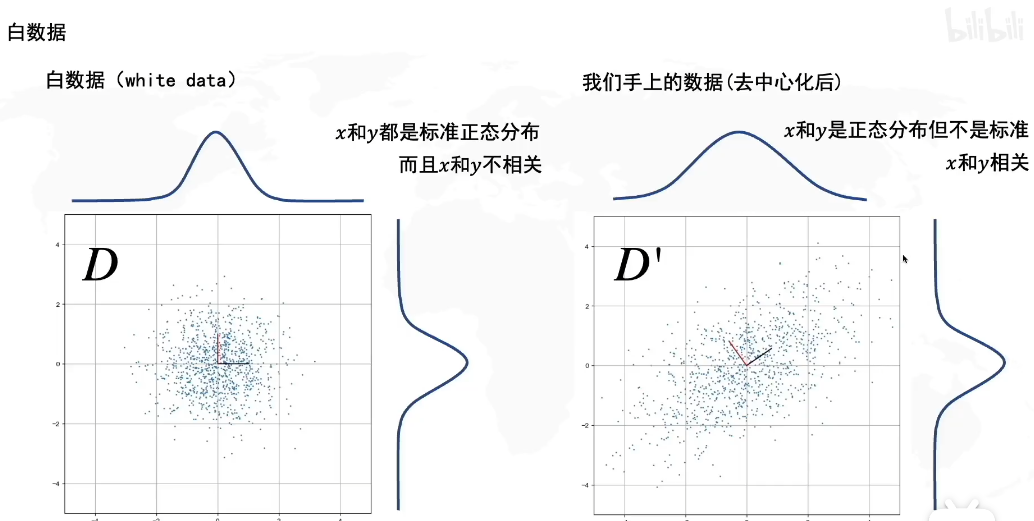
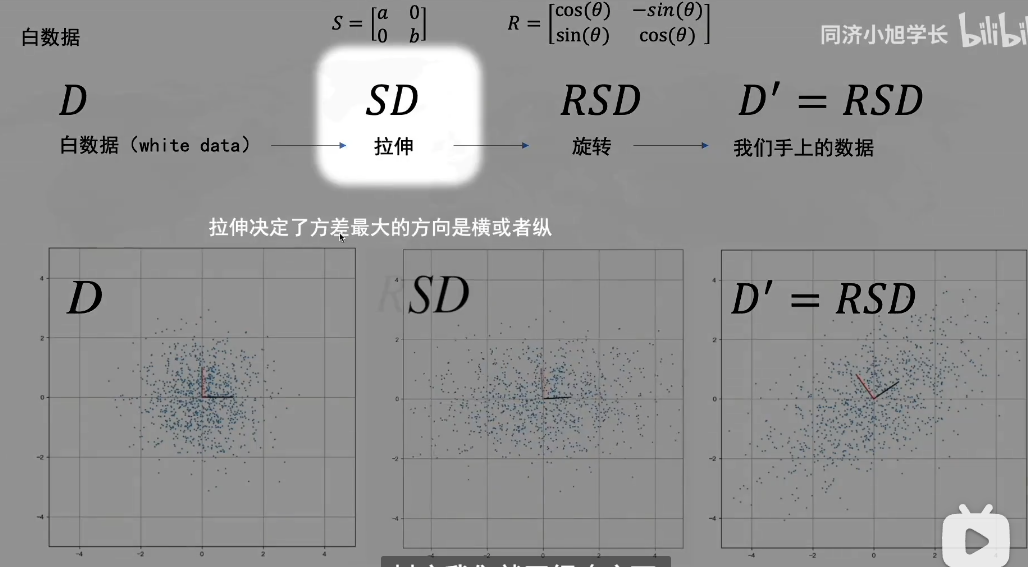
拉伸的方向就是方差最大的方向

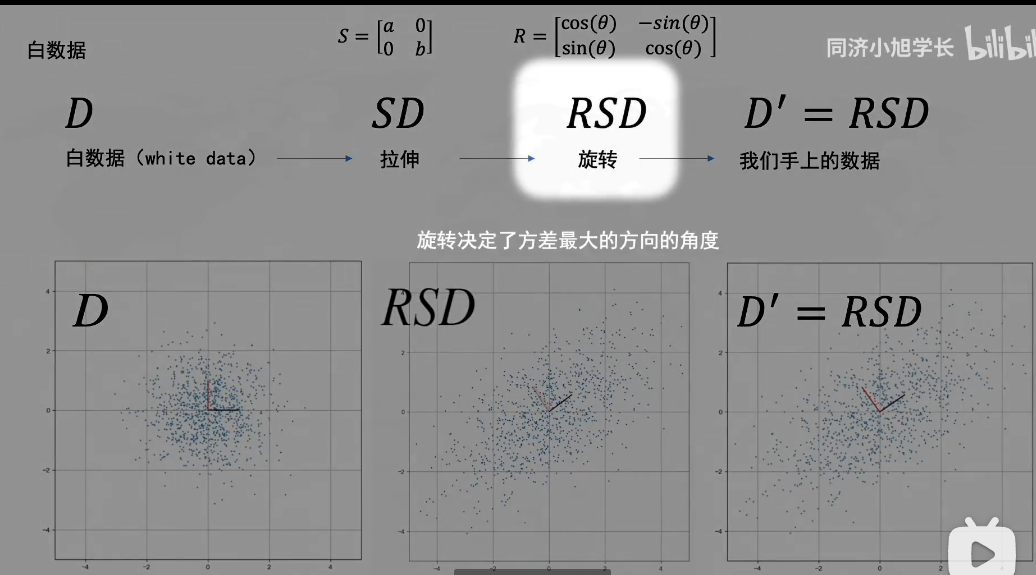
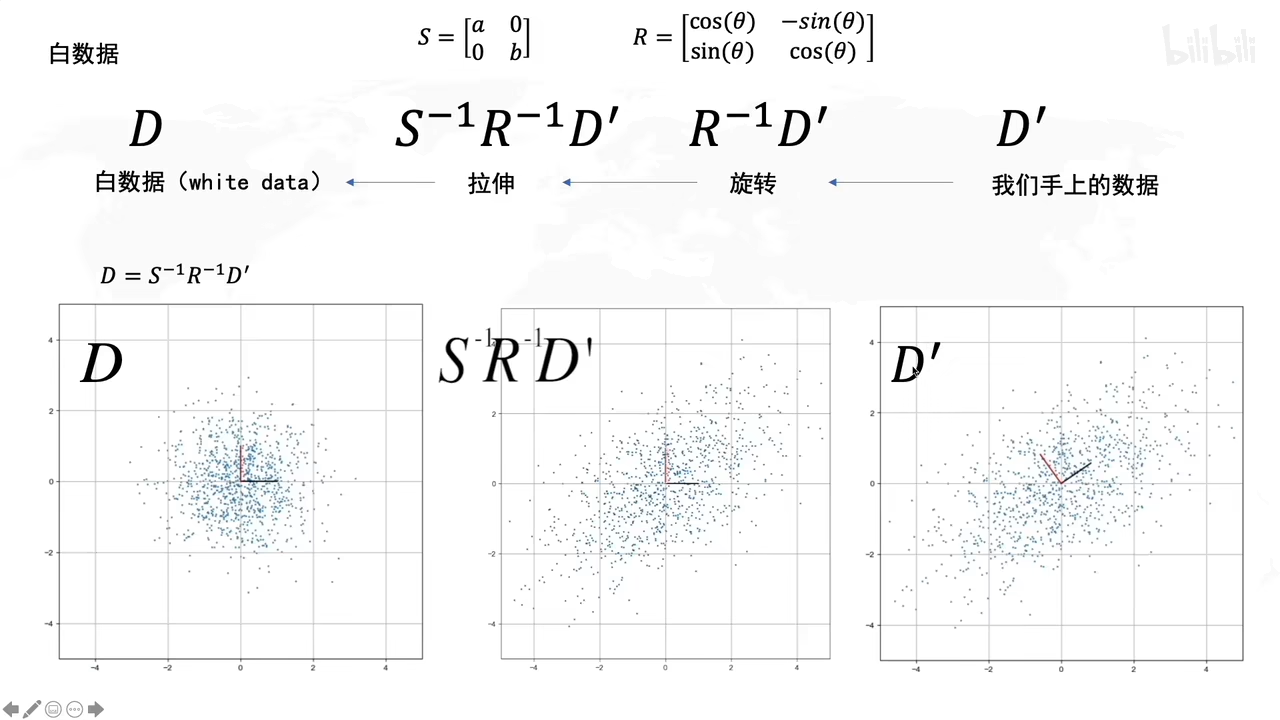
D’转化成原先矩阵D，就用各自的逆矩阵乘回来。

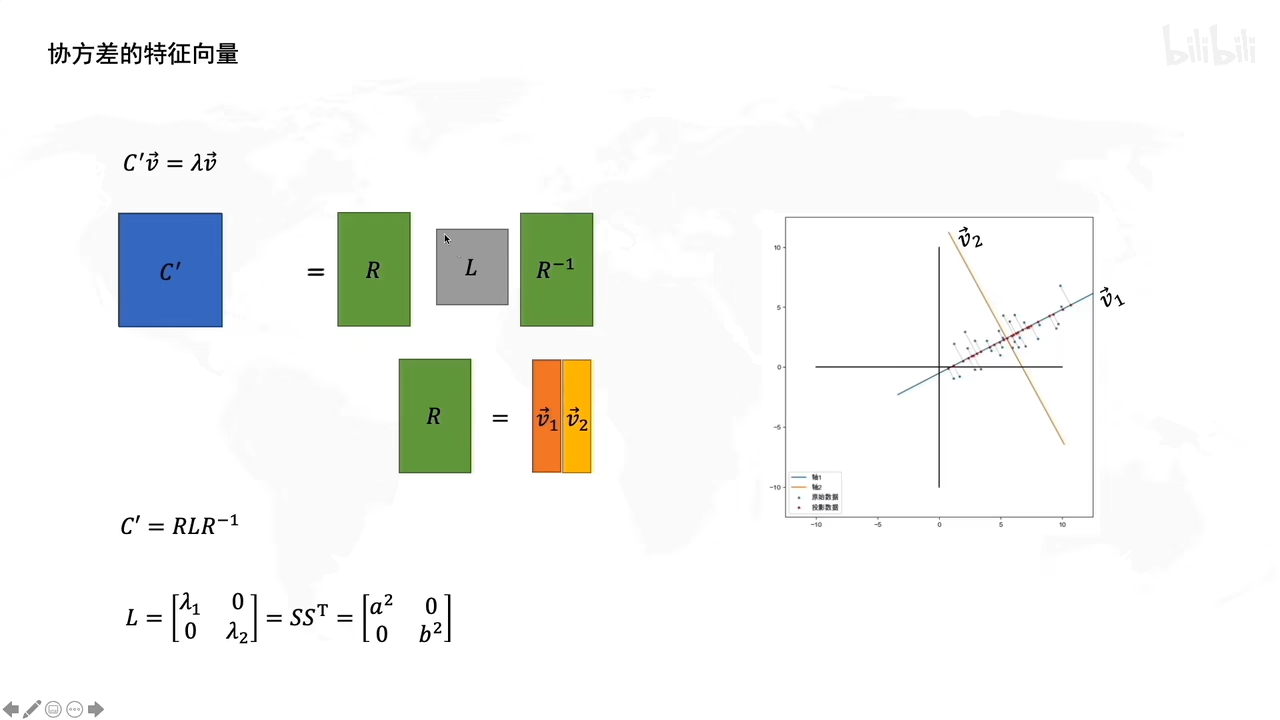
怎么求R呢

协方差的特征向量就是R

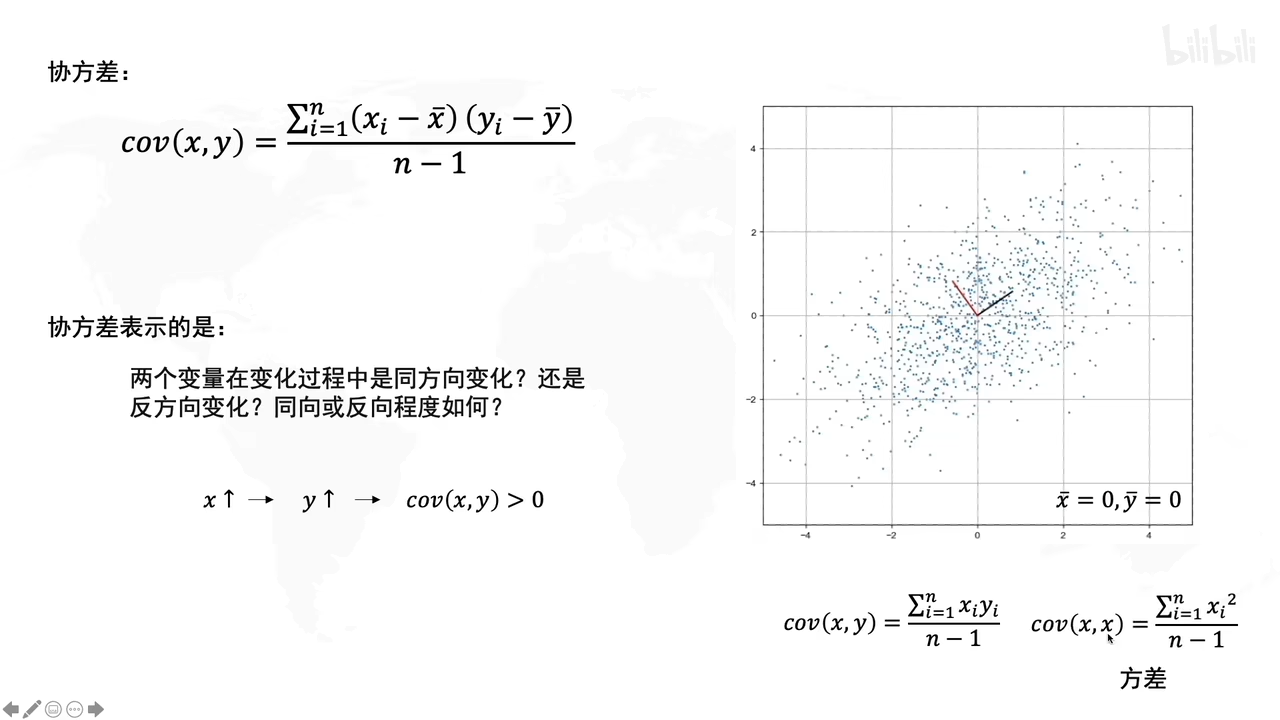
啥是协方差？

协方差矩阵是啥？

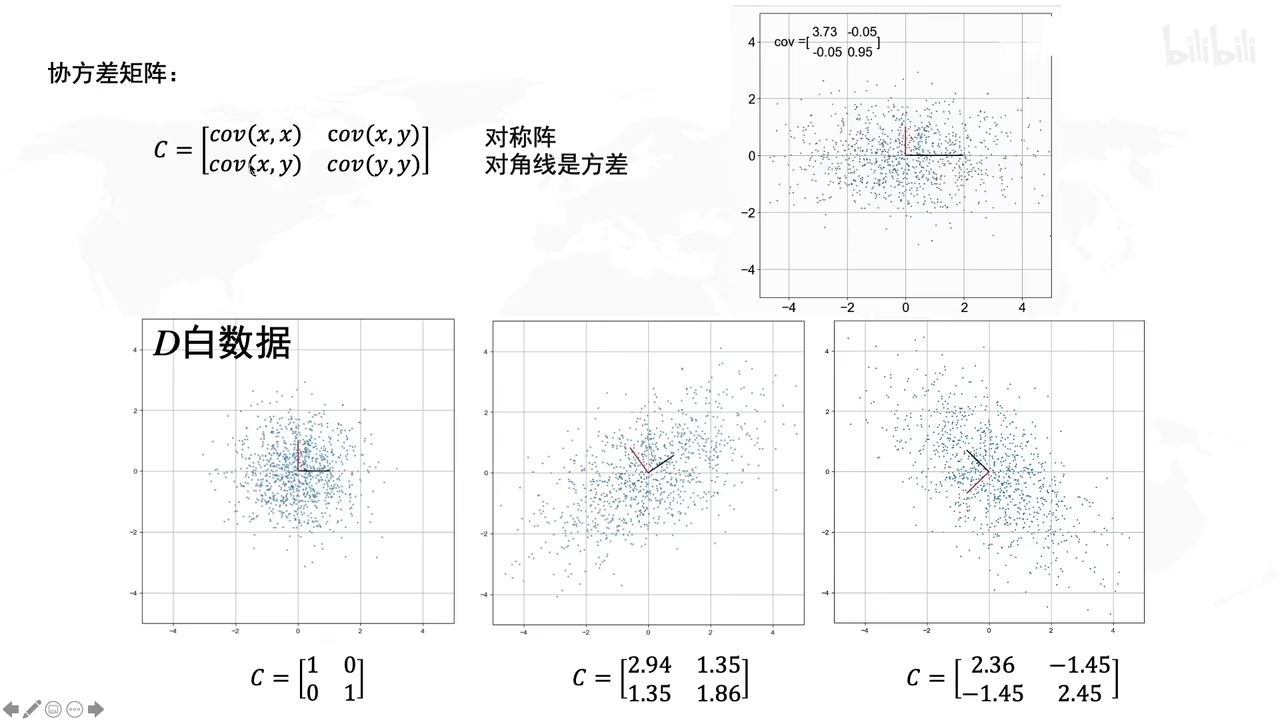
若x，y是不相关的话，那么cov（x，y）就是0

上图，

第一个小图就是x，y不相关

第二个小图就是x，y正相关（协方差大于0）

第二个小图就是x，y负相关（协方差小于0）

为什么是n-1？

（因为保证统计量的无偏性，保守估计比真实值偏大）

用白数据加上拉伸和旋转后，就得到D’

开始公示推导：（D’符合一般正态分布，可以标准化后与D一样的特性）

特征向量求解

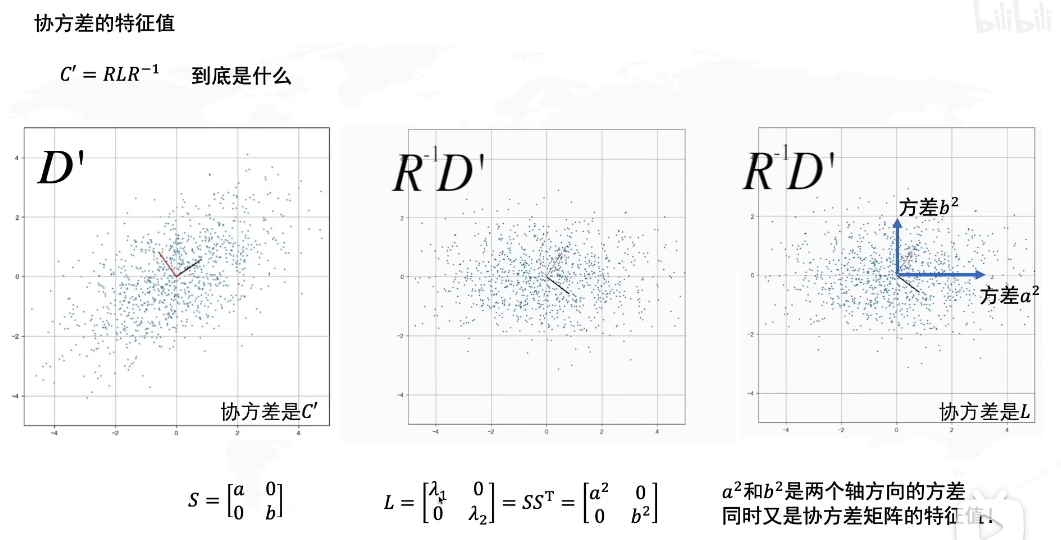
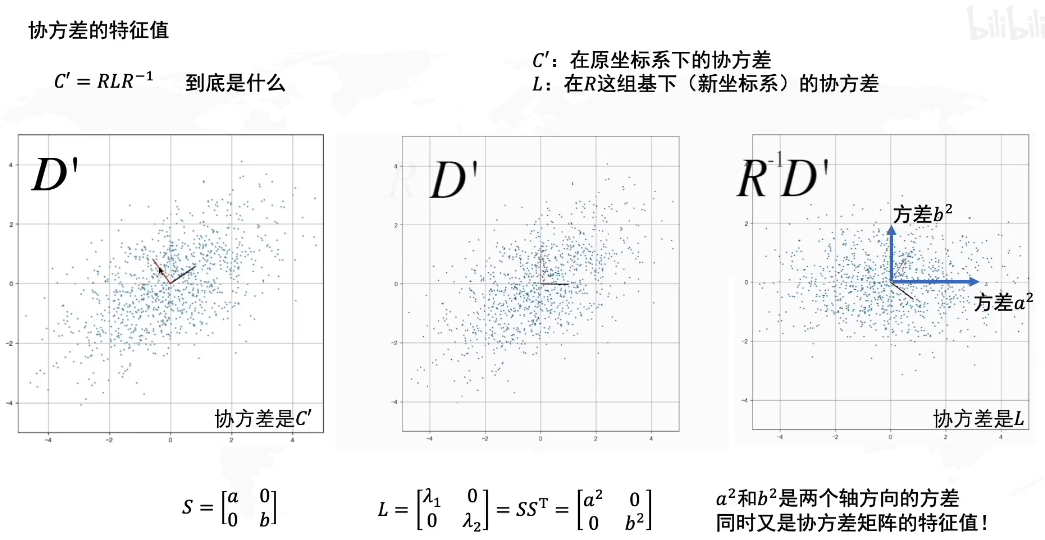
总结了：

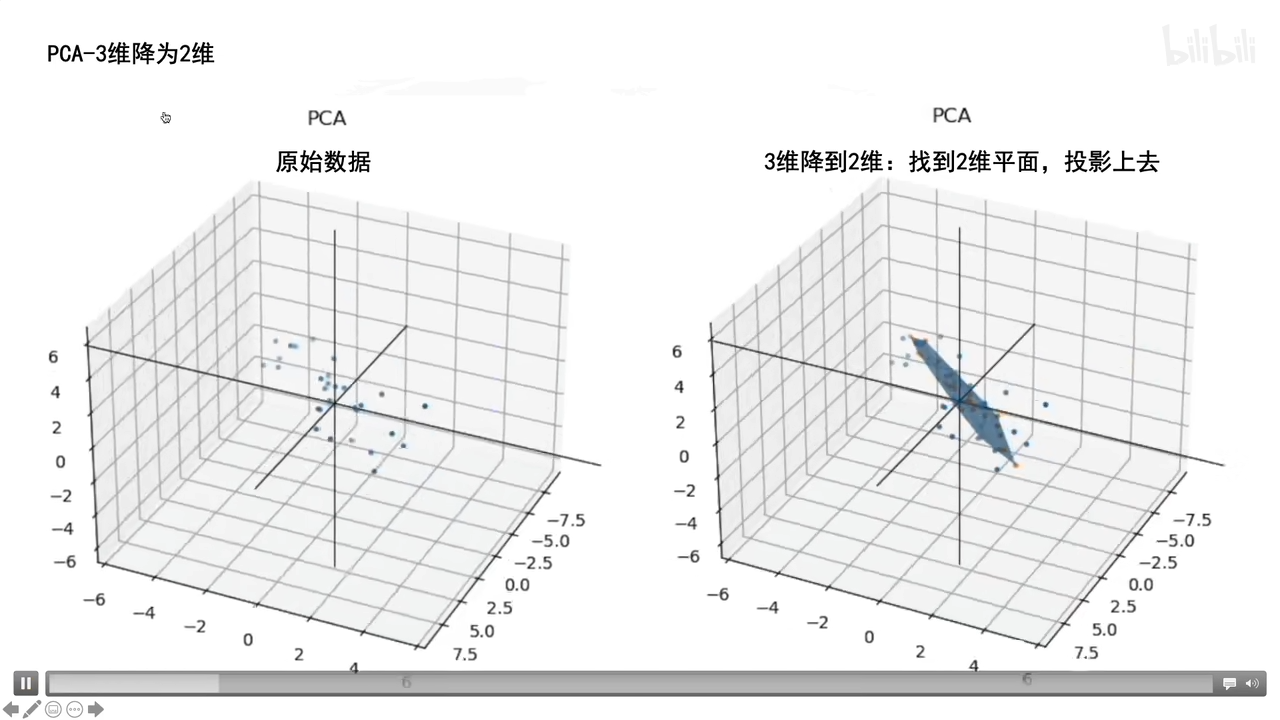
三维转二维就是找个二维平面然后投影，（让数据间方差最大的）

PCA和置信椭圆有什么关系？

（啥是置信椭圆？？？

置信椭圆基本上是对置信区域的描述方式，其长轴和短轴分别为置信区域的参数，置信椭圆的长短半轴，分别表示二维位置坐标分量的标准差（如经度的σλ和纬度的σφ）。

）

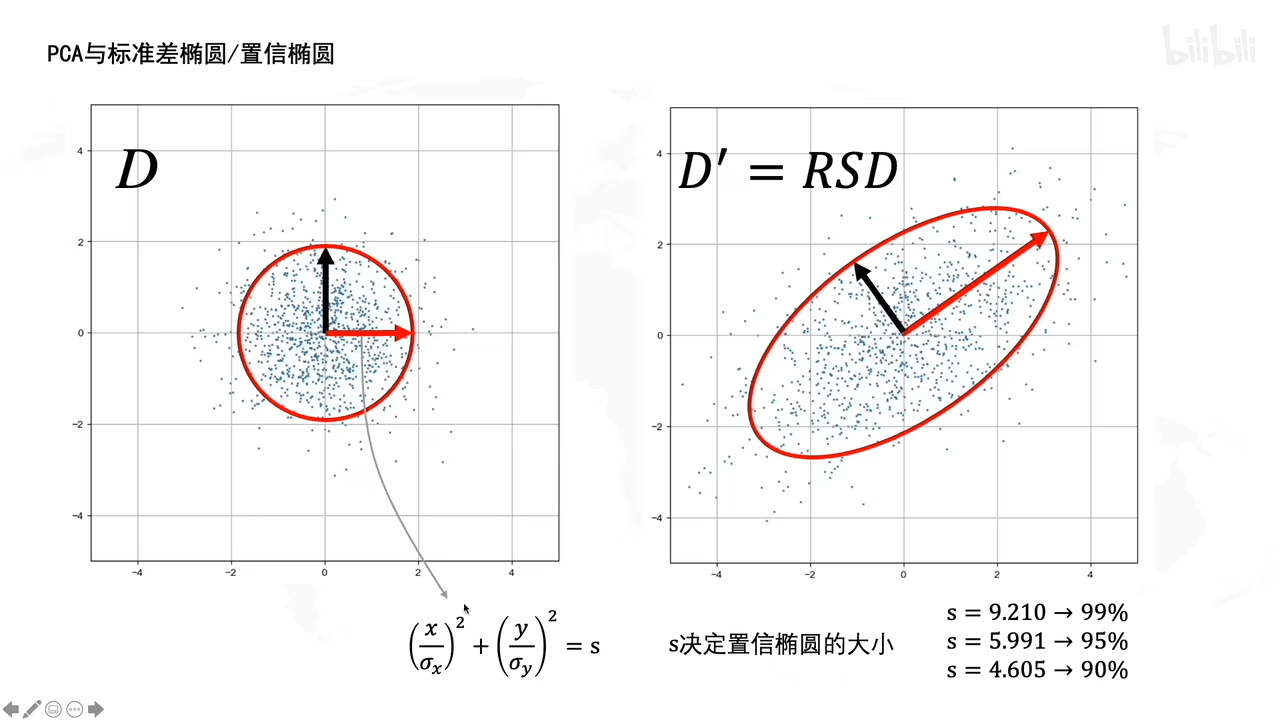
从白数据里面画了一个圆，（刚好有0.95的数据在圆内）拉伸旋转后成了一个圆，还是有0.95的数据点在椭圆里

与奇异值分解的关系

t_SNE

中心极限定理（前置知识）

什么是中心极限定理

中心极限定理指的是给定一个任意分布的总体。我每次从这些总体中随机抽取n 个抽样，一共抽m次。然后把这m组抽样分别求出平均值。这些平均值的分布接近正态分布。 （因此，某些题可以转化为正态分布而使用相关结论）

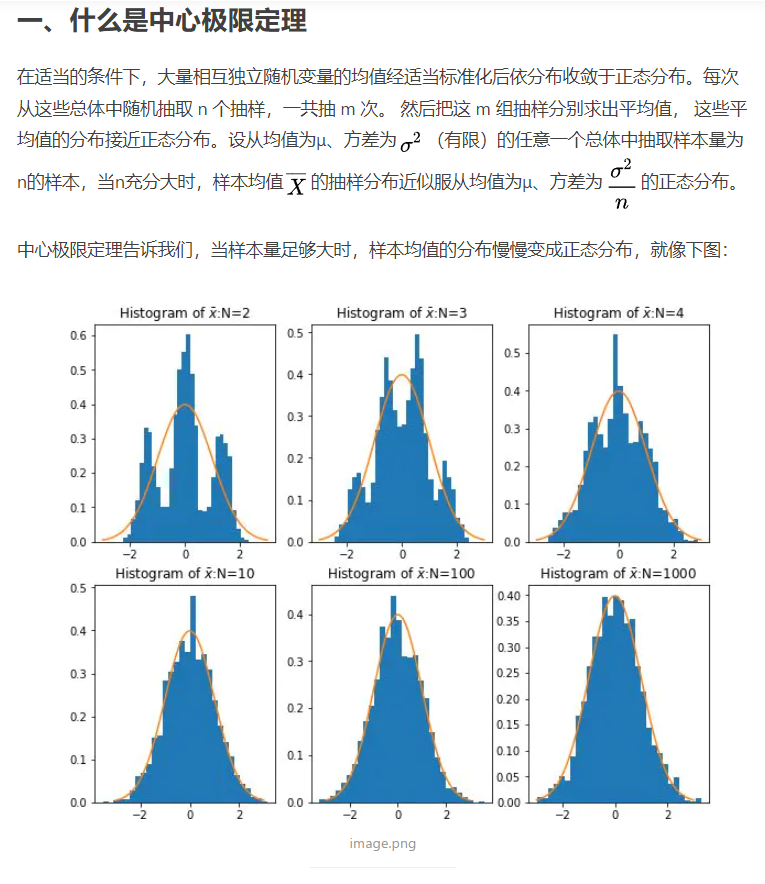
如果整体分布的标准差未知，可以通过m次抽样中的一次的标准差来代替

假设检验（前置知识）

假设检验_一篇搞懂假设检验

自由度（前置知识）

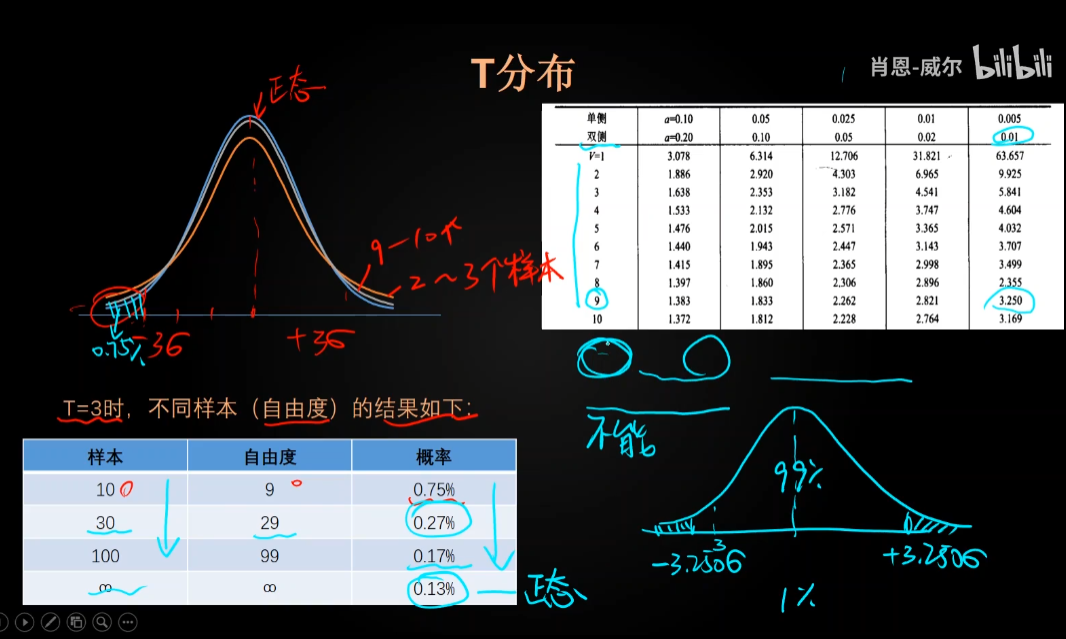
T分布

t分布（t distribution）- 统计学
定性分析：

定量分析：

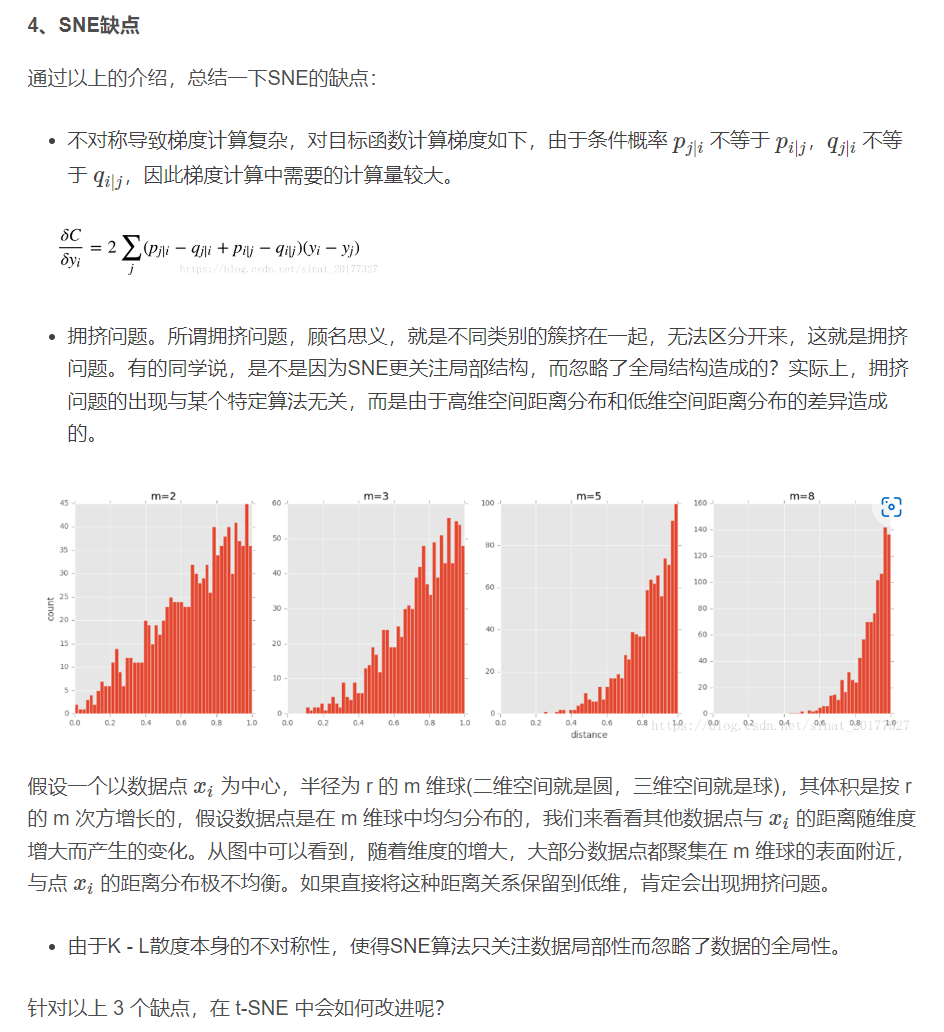
t-SNE算法

常见的降维算法：

1. 主成分分析(线性)
2. t-SNE (非参数/非线性)
3. SNE(非线性)

无监督学习-深度生成模型I

图像处理-创作

1. 有关generation model，这里有一篇很好的reference。在这篇reference里开头引用Richard Feynman的话。这句话来自Richard Feynman办公室黑板上一句话：“why i cannot creater, i do not understand”。所以一个东西，不知道咋样产生它的话就不是完全理解。
2. 所以，对machine来说是一样的。比如machine在影像处理上可以做到分类，可以辨识猫和狗的不同。但它并不真的了解猫什么，狗是什么。也许在未来有一天，machine它可以画出一只猫，它会猫这个概念或许就不一样了。这是一个非常热门的主题，有很多相关的研究，我们来看一下相关的研究。
   
3. 在这些研究里，大概可以分为三个方法。分别是：PixelRNN, VAE, Generative Adversarial Network(GAN)，这些方法其实都非常新，其中最旧的是VAE(2013年提出来的)，GAN是2014年提出来的
   

PixelRNN

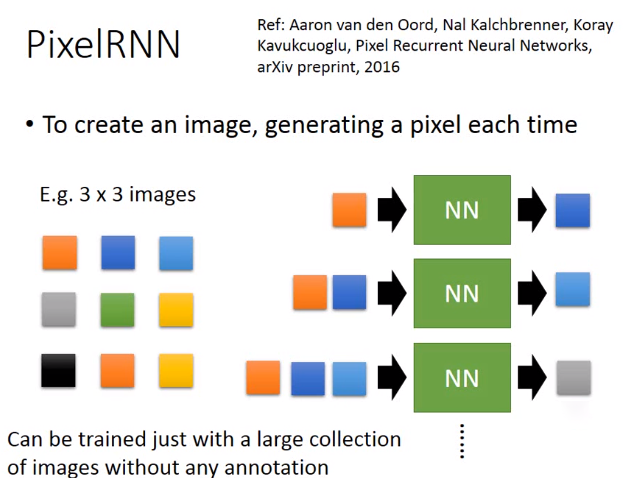
你可能很直觉的说：一个pixel就是一个用三维的vector(三个数字)来描述它(每一个数字代表了RGB)。比如：如果有一个pixel用三个channel来表示(R=50, G=150,B=100)，我实际上这样做感觉实际结果不是太好，我觉得一个原因是因为是：**你这样做，产生的图都很灰。如果你要产生鲜明颜色的话，RGB某一个value特别高，其他都接近于0(RGB三个value都差不多就是灰色)。但是你在learn的时候，你往往没有办法真的让B=0或者G=0。**如果你今天把0-255 normalization 0-1，你用sigmoid function的话，通通落在0.5左右(中间)，很难落子极端的值。所以它产生的值都差不多，所以每张图看起来都是灰色的，看起来就不是那么的好看。

所以我做了一下处理，我把**每一个pixel都用a 1-of-N encoding来表示，在这个1-of-N encoding里面，每一个dimension就代表了一个颜色。也就是说：每一个pixel都是用一个vector来表示，第一个dimension代表黄色，第二个dimension代表蓝色，第三个dimension代表绿色等。也就是说不让它RGB去合成颜色，而是让它产生一个颜色。**假设一个绿色进来，就是第三维是1，其他为0，所以一个pixel我们用这种方式来描述它。

但是有一个问题是：颜色太多了，RGB可能都会有(256的三次方)，有太多可能的颜色。肿么办呢？我先做**clustering，**把同样接近的颜色cluster在一起。也就是说：这三个绿算是同一种颜色，都用上面这一个绿来表示它。那我把出现颜色比较少的颜色跟出现次数比较多的颜色把它合并起来，所以得到了176种不同的颜色。

刚才是给machine一个开头让它画下去，接下里就什么都不给它，让它从头就开始画。但是你什么都不给它，让它从头开始画的话，它可能每一张image都是一样的，所以你要故意加一些random，也就是说它要predict下一个pixel的时候，不见得是选几率最后的那个pixel，它会有一定几率选一个几率比较低的颜色出来画在图上面，这样它每一次画的图都才会有点不一样。

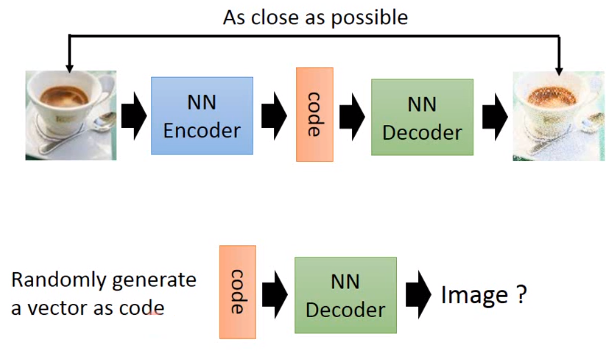
自动编码器

我们之前已经有讲过Auto-encoder，那我们在讲Auto-encoder的时候，input一张image通过encoder变成code，再通过decoder把这个image解回来，希望input跟output越接近越好。你learn完这个auto-encoder以后，你其实就可以把这个decoder拿出来，然后你再给它input一个randomly的vector，把这个random vector当做code,code是10维，那你就是generate 10维的vector，然后丢到decoder里面，它output就可以是一张完整的image

无监督学习-深度生成模型II

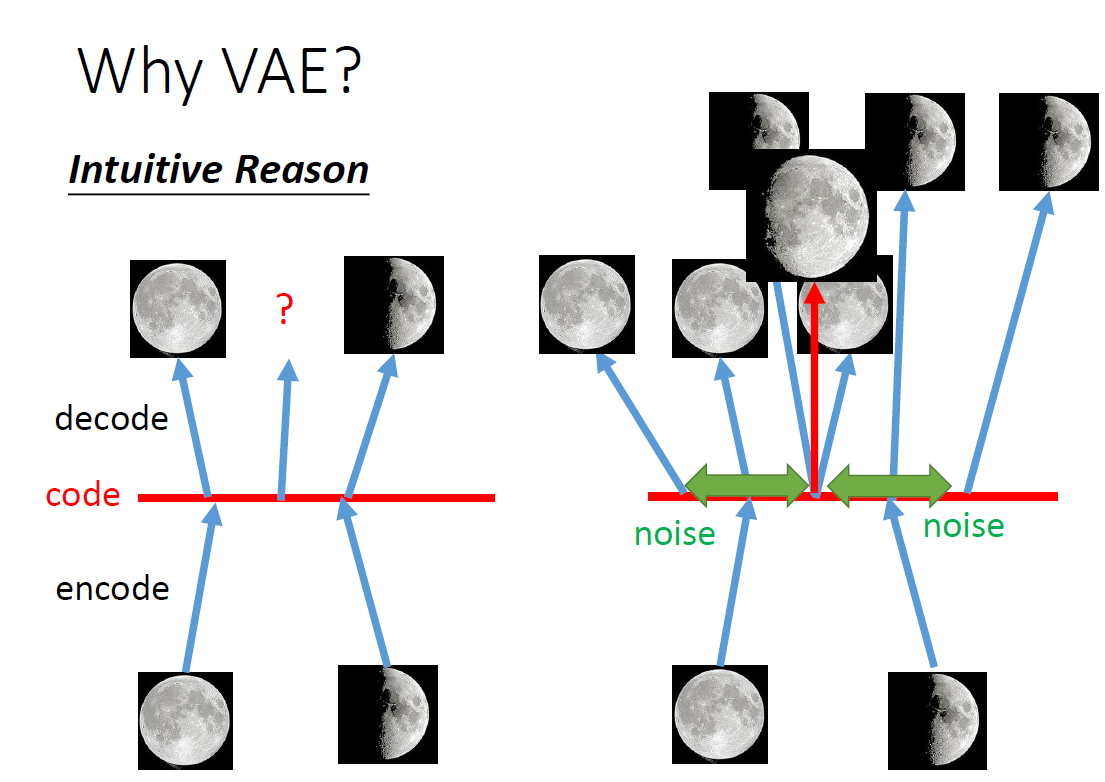
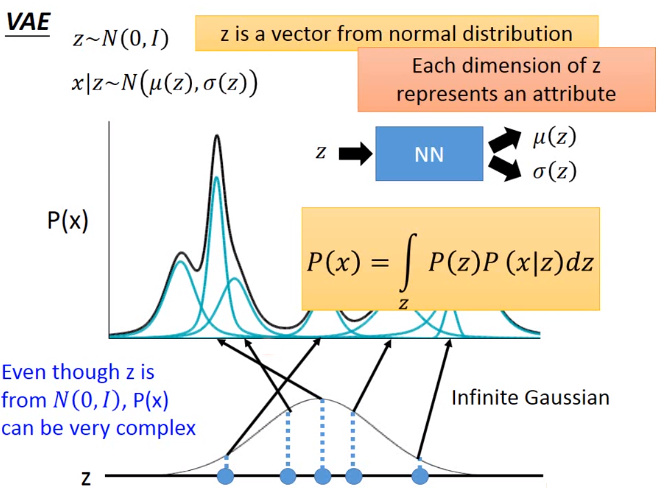
为什么要用VAE？

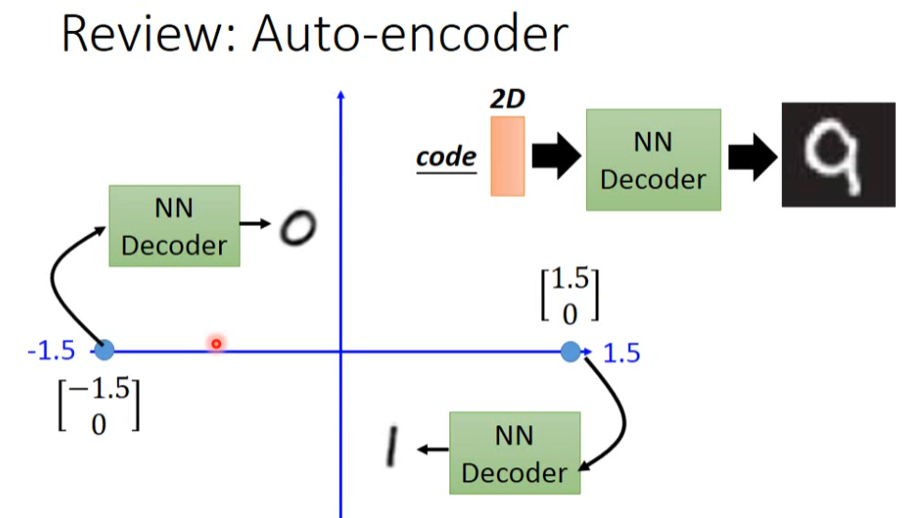
我们来看intuitive reason，为什么要用VAE？如果是原来的auto-encoder的话，做的事情是：把每一张image变成一个code，假设现在的code是一维(图中红色的线)。你把满月这个图变为code上的一个value，在做decoder变回原来的图，半月图也是一样的。假设我们在满月和半月code中间，sample一个点，然后把这个点做decoder变回image，他会变成什么样子呢？你可能会期待说：可能会变成满月和半月之间的样子，但这只是你的想象而已。因为我们今天用的encoder和decoder都是non-linear的，都是一个neural network，所以你很难预测在这个满月和半月中间到底会发生什么事情。

那如果用VAE会有什么好处呢？VAE做事情是：当你把这个满月的图变成一个code的时候，它会在这个code上面再加上noise，它会希望加上noise以后，这个code reconstruct以后还是一张满月。也就是说：原来的auto-encoder，只有中间这个点需要被reconstruct回满月的图，但是对VAE来说，你会加上noise，在这个范围之内reconstruct回来都要是满月的图，半月的图也是一样的。你会发现说：在这个位置，它同时希望被reconstruct回满月的图，又希望被reconstruct回半月的图，可是你只能reconstruct一张图。肿么办？VAE training的时候你要minimize mean square，所以这个位置最后产生的图会是一张介于满月和半月的图。所以你用VAE的话，你从你的code space上面去sample一个code再产生image的时候，你可能会得到一个比较好的image。如果是原来的auto-encoder的话，得到的都不像是真实的image。

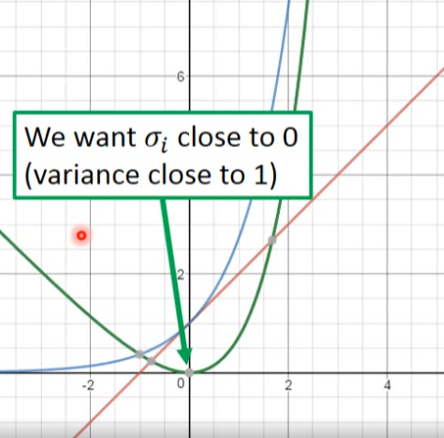
所以这个encoder output m代表是原来的code，这个c代表是加上noise以后的code。decoder要根据加上noise以后的code把它reconstruct回原来的image。 σ 代表了noise的variance，e是从normal distribution sample出来的值，所以variance是固定的，当你把 σ 乘上e再加上m的时候就等于你把原来的code加上noise，e是从normal distribution sample出来的值，所以variance是固定的，但是乘上一个σ 以后，它的variance 大小就有所改变。这个variance决定了noise的大小，这个variance是从encoder产生的，也就是说：machine在training的时候，它会自动去learn这个variance会有多大。

但是如果还是这样子还是不够的，假如你现在的training只考虑：现在input一张image，中间有加noise的机制，然后dec oder reconstruct回原来的image，然后minimize 这个reconstruct error，你只有做这件事情是不够的，你training的出来的结果并不会如你所预期的样子。

从科学角度解释：
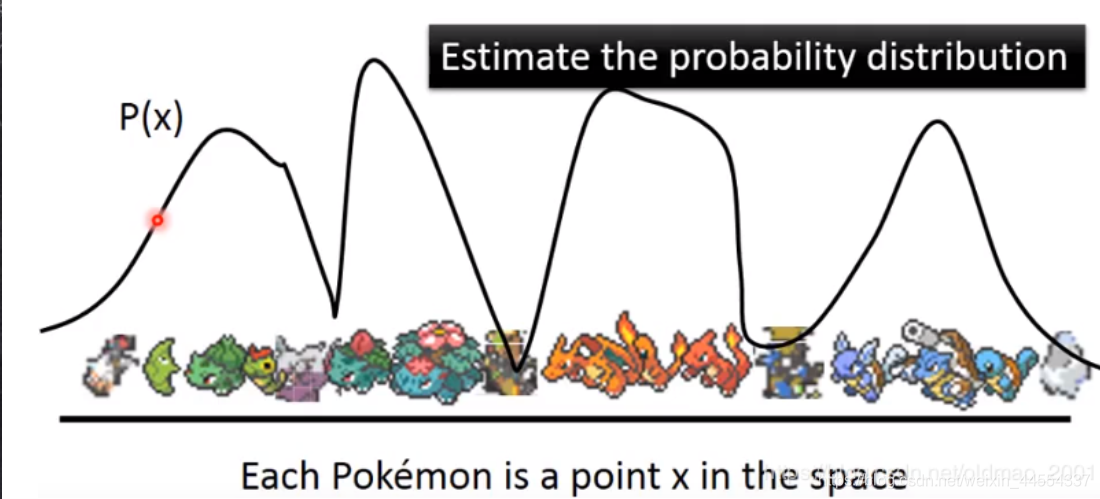
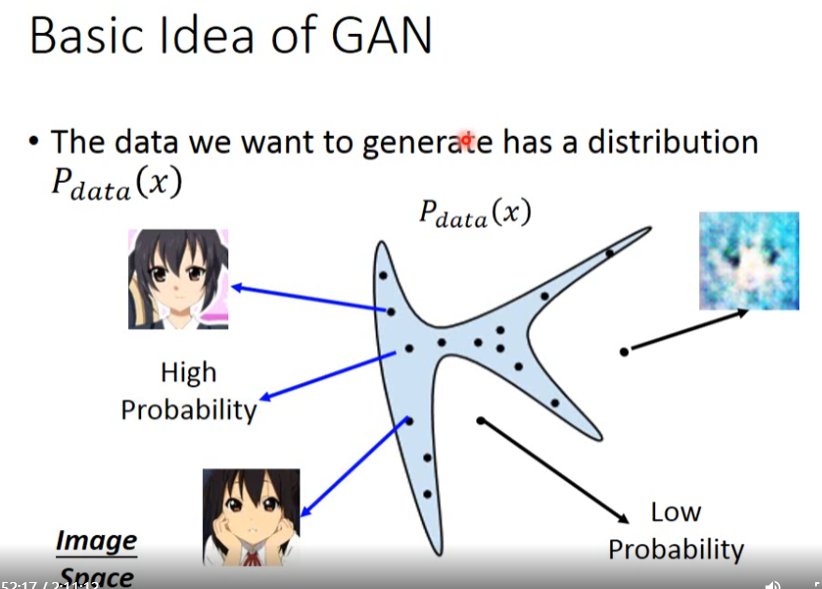
先明确一下目标:宝可梦分布
P(x):Maxminim ,如果图形越接近宝可梦P(x)就越大，图形乱七八糟P(x)就越小。

GMM:要估计P(x)就要用GMM

高斯混合模型

每一个x都是从某一个mixture被sample出来的，这件事情其实就很像是做classification一样。我们每一个所看到的x，它都是来自于某一个分类。但是我们之前有讲过说：把data做cluster是不够的，更好的表示方式是用distributed representation，也就是说每一个x它并不是属于某一个class，而是它有一个vector来描述它的各个不同面向的特性。所以VAE就是gaussion mixture model distributed representation的版本。

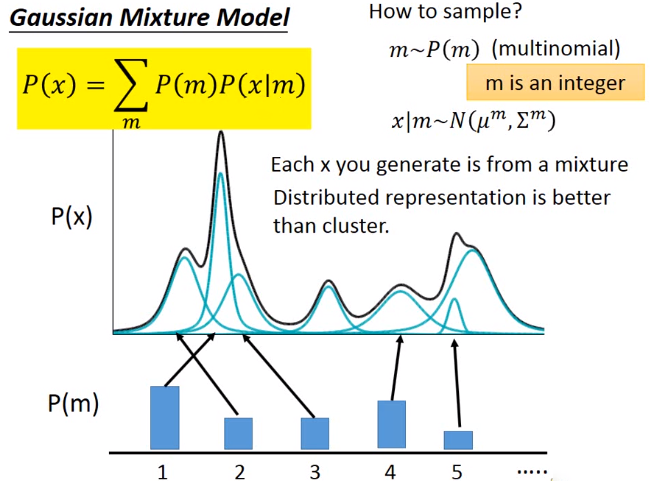
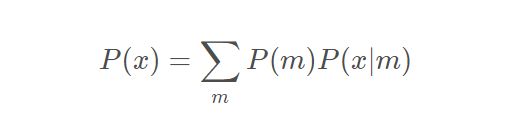
P(m)是组成混合高斯的每一个小高斯的权重，一共有m个高斯
如何从这m个简单高斯分布中sample 数据呢？
先要决定从哪一个高斯进行sample，也就是把这些个高斯分布看做一个multinomial的问题
于是这个决定的过程可以看做是一个关于m个样本的采样，从第m个高斯采样的概率是P(m) *找到指定的高斯了以后，再根据这个高斯的参数(μm,Σm )进行采样：

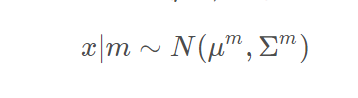
这里就很明白了，公式P(x) 中P(m)**是选择第m个高斯的概率，也可以看做权重；P(x∣m)可以看做是从第m个高斯取数据x的概率。
现在如果我们手上有一系列的数据x（可以看到的，也叫观察变量），现在要估计m个高斯分布（看不到的，也叫隐变量）的各个参数(μm,Σm)，就是用EM算法。

最大化可能性

VAE的问题

VAE其实有一个很严重的问题就是：它从来没有真正学咋样产生一张看起来像真的image，它学到的东西是：它想要产生一张image，跟我们在database里面某张image越接近越好。但它不知道的是：我们evaluate它产生的image跟database里面的相似度的时候(MSE等等)，decoder output跟真正的image之间有一个pixel的差距，不同的pixel落在不同的位置会得到非常不一样的结果。假设这个不一样的pixel落在7的尾部(让7比较长一点)，跟落在另外一个地方(右边)。你一眼就看出说：右边这是怪怪的digit，左边这个搞不好是真的(只是长了一点而已)。但是对VAE来说都是一个pixel的差异，对它来说这两张image是一样的好或者是一样的不好。

所以VAE学的只是咋样产生一张image跟database里面的一模一样，从来没有想过：要真的产生可以一张以假乱真的image。所以你用VAE来做training的时候，其实你产生出来的image往往都是database里面的image linear combination而已。因为它从来都没有想过要产生一张新的image，它唯一做的事情就是模仿而已

所以接下来有了一个方法Generative Adversarial Network(GAN)，最早出现在2014年。

GAN

GAN的概念像是拟态的演化，如图是一个枯叶蝶(长的像枯叶一样)，枯叶蝶咋样变得像枯叶一样的呢？也许一开始它长是这个样子(如左图)。但是它有天敌(麻雀)，天敌会吃这个蝴蝶，天敌辨识是不是蝴蝶的方式：它知道蝴蝶不是棕色的，所以它吃不是棕色的东西。所以蝴蝶就演化了，它就变成了棕色的了。它的天敌会跟着演化，天敌知道蝴蝶是没有叶脉的，所以它会吃没有叶脉的东西。所以蝴蝶演化变成枯叶蝶(有叶脉)，它的天敌也会演化，蝴蝶和它的天敌会共同的演化，枯叶蝶会不断的演化，直到和枯叶无法分别为止。

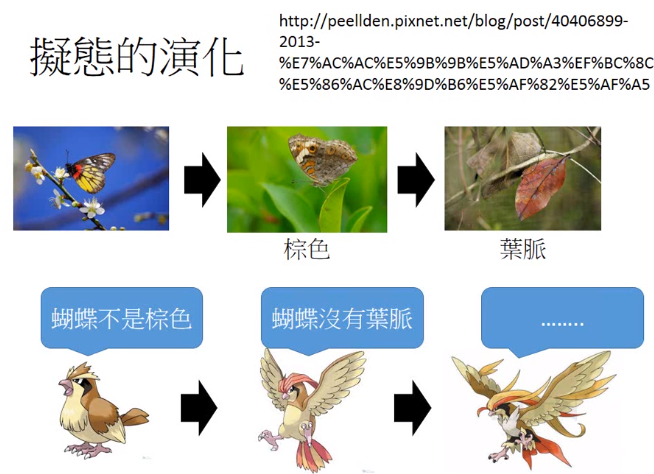
所以GAN的概念是非常类似的，首先有第一代的generator，generate一些奇怪的东西(看起来不是像是image)。接下来有第一代的Discriminator(它就是那个天敌)，Discriminator做的事情就是：它会根据real images跟generate产生的images去调整它里面的参数，去评断说：这是真正的image还是generate产生的 image。接下来generator根据discriminator调整了下它的参数，所以第二代generator产生的digit更像是真的image，接下来discri minator会根据第二代generator产生的digit跟真正的digit再update它的参数。接下来产生第三代generator，产生的digit更像真正的数字(第三代generator产生的digit可以骗过第二个discri minator)，但是discri minator也会演化，等。

The evolution of generation

你要注意的一个地方就是：这个Generator它从来没有看过真正的image长什么样子，discri- minator有看过真正的digit长什么样子，它会比较正真正的image和generator的不同，它要做的就是骗过discri-minator。generator没有看过真正的image，所以generate它可以产生出来的image是database里面从来都没有见过的，这比较像是我们想要machine做的事情。

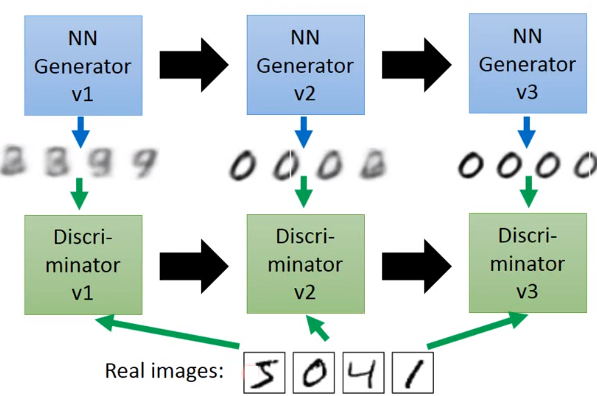
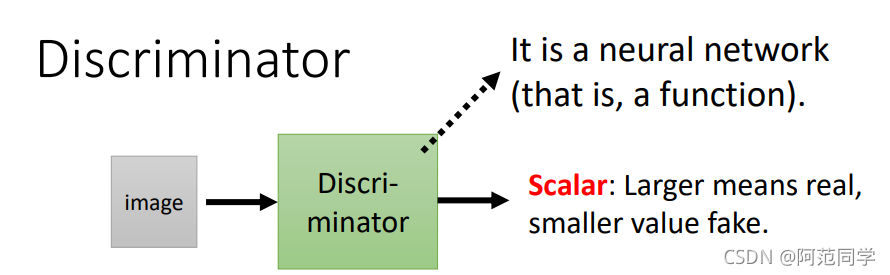
我们来看discriminator是咋样train的：这个discriminator就是一个neural network，它的input就是一张image，它的output就是一个number(可以通过sigmoid function让值介于0-1之间，1代表input这一张image是真正的image，0代表是generator所产生的)。generator在这里的架构其实就跟VAE的decoder是一摸一样的，它也是neural network，它的input就是从一个distribution sample出来的vector，你把sample出来的vector丢到generator里面，它就会产生一个数字(image)，你给它不同的vector，它就会产生不同样子的image，先用generator产生一堆image(假的)。我们有真正的image，discriminator就是把generator所产生的image都label为0，把真正的image都label为1。

GAN的全名是Generative Adversarial Network生成对抗网络，其主要的目的是为了让训练机器让机器能够自主生成相对应类型的图片，其中生成器generator就是GAN中进行生成相对应类似分布的网络，而鉴别器Discriminator就是判别生成器生成是否为真假的网络，鉴别器通过将输入的图像转换成一个判别值来判断真假，值越大，图像越真实，目前的GAN已经发展了许多的种类，有各式各样的GAN网络。

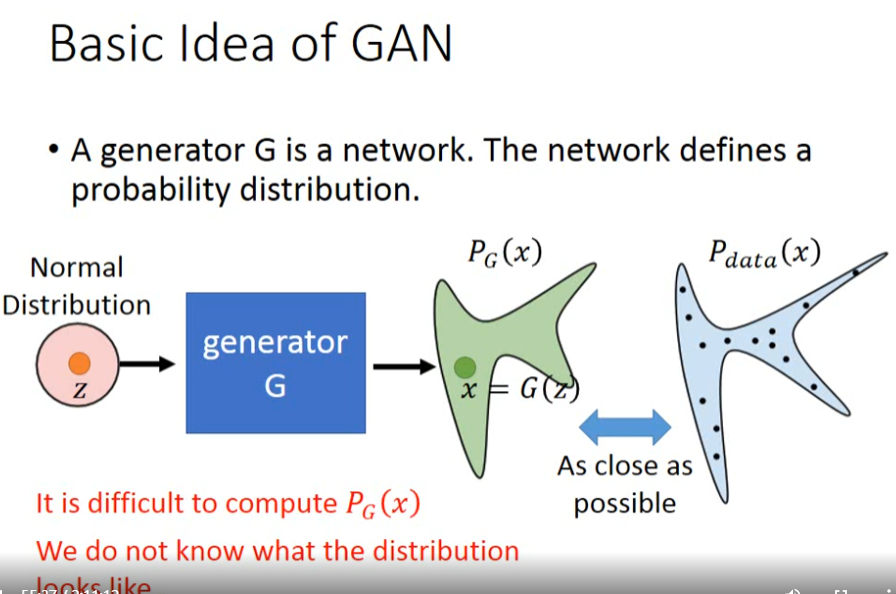
GAN中生成器的目标是将输入的正态分布数据经过生成网络变成类似真实标签分布的数据，而为了让分布尽可能相似就必须最小化两个数据分布之间的距离

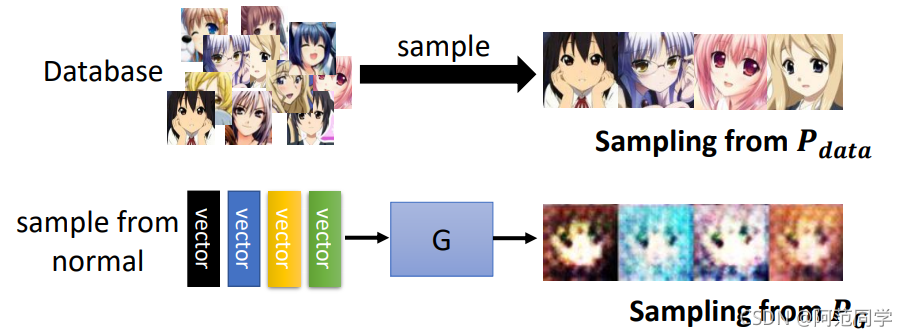
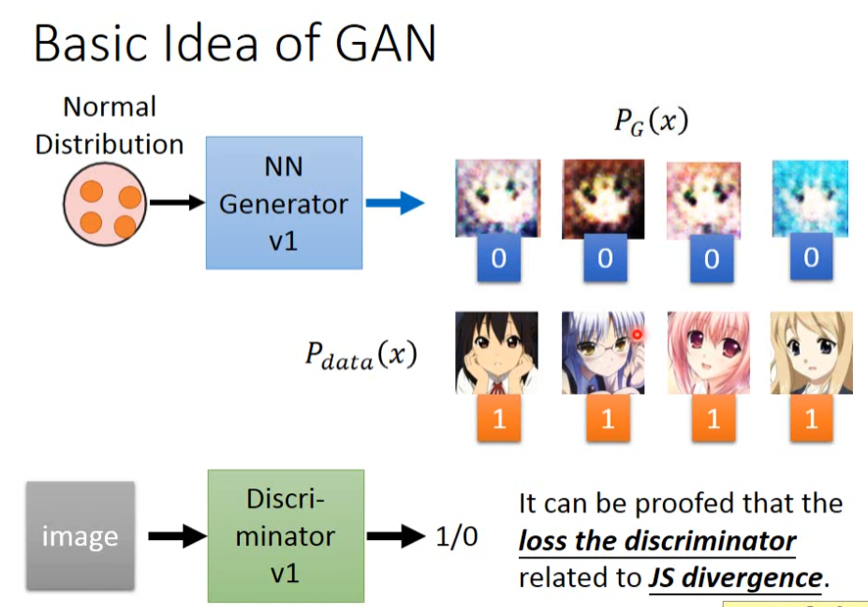
Step 1：初始化生成器和判别器的参数
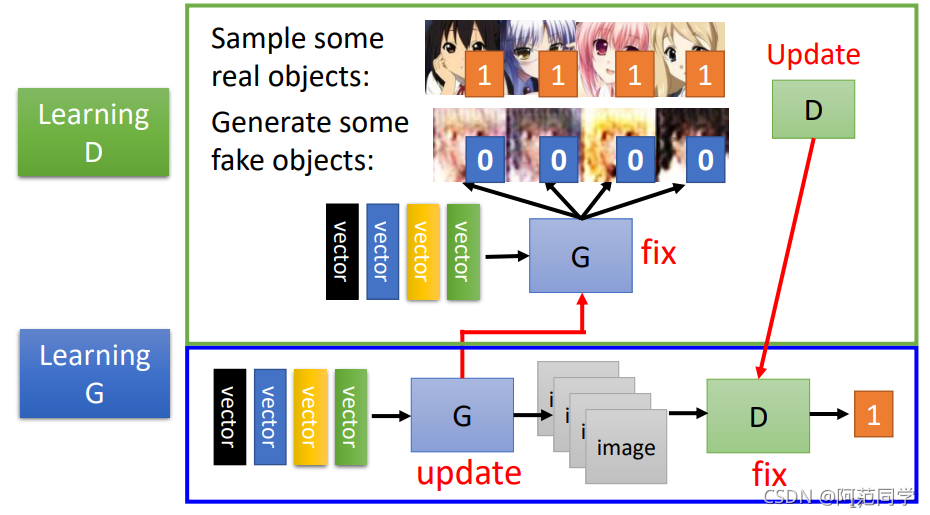
Step 2：固定住生成器更新判别器，判别器给生成器的生成图像打低分给真实标签图像打高分
Step 3：固定住判别器更新生成器，生成器通过输入的随机采样的vector生成图像尝试骗过判别器使其让它打高分。

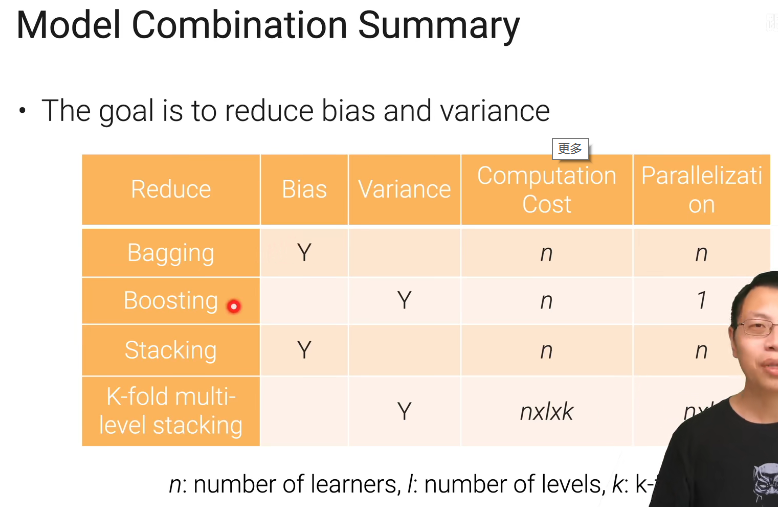
集成学习

个体与集成

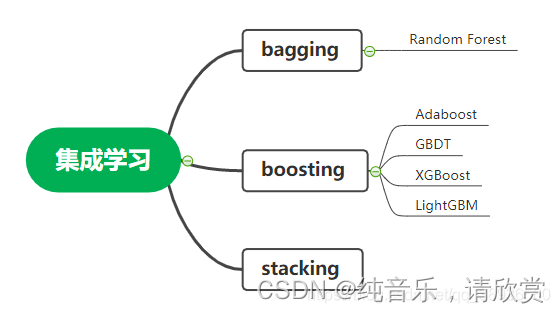
一般在kaggle之类的比赛中，ensemble用的最多的也是效果最好的，一般前几名都需要用ensemble。

Bagging

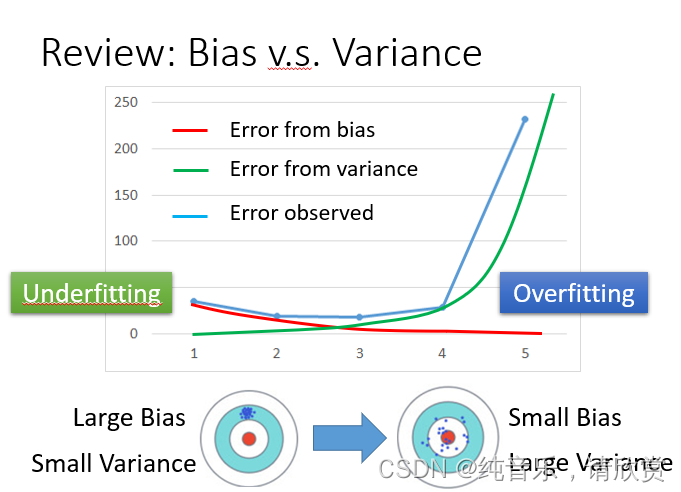
我们先来回顾一下bias和variance，**对于简单的模型，我们会有比较大的bias但是有比较小的variance，如果是复杂的模型，我们则是比较小的bias但是有比较大的variance。**从上图上看，在这两者的组合下，我们最后的误差（蓝色的线）会随着模型数目的增加，先下降后逐渐上升。

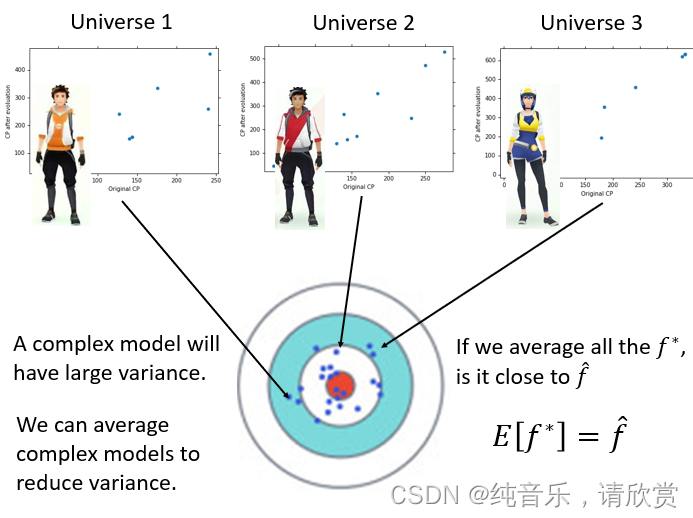
在之前的宝可梦例子中，根据不同的事件我们会得到一个模型，如果一个复杂的模型就会有很大的variance。这些模型的variance虽然很大，但是bias是比较小的，所以我们可以把不同的模型都集合起来，把输出做一个平均，得到一个新的模型\hat{f}​ ，这个结果可能和正确的答案就是接近的。Bagging就是要体现这个思想。 Bagging就是我们自己创造出不同的dataset，再用不同的dataset去训练一个复杂的模型，每个模型独自拿出来虽然方差很大，但是把不同的方差大的模型集合起来，整个的方差就不会那么大，而且偏差也会很小。

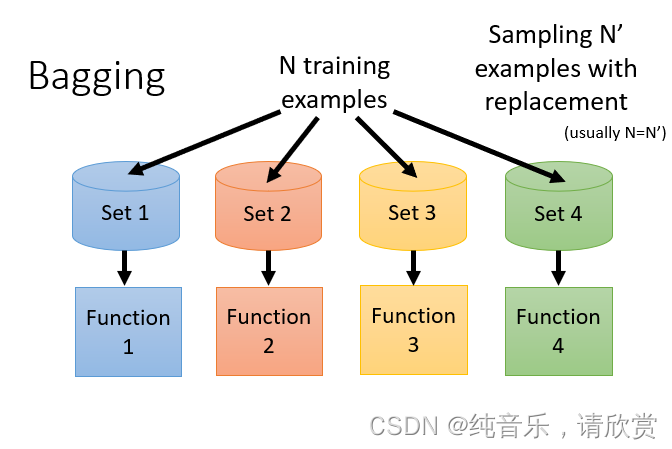
上图表示了用自己采样的数据进行Bagging的过程。在原来的N笔训练数据中进行采样，过程就是每次从N笔训练数据中取N‘（通常N=N’）建立很多个dataset，这个过程抽取到的可能会有重复的数据，但是每次抽取的是随机形成的dataset。每个dataset都有N’笔data，但是每个dataset的数据都是不一样的，接下来就是用一个复杂的模型对四个dataset都进行学习得到四个function，接下来在testing的时候，就把这testing data放到这四个function里面，再把得出来的结果做平均（回归）或者投票（分类），通常来说表现（variance比较小）都比之前的好，这样就不容易产生过拟合。

做Bagging的情况：模型比较复杂，容易产生过拟合。（容易产生过拟合的模型：决策树）目的：降低方差。

决策树

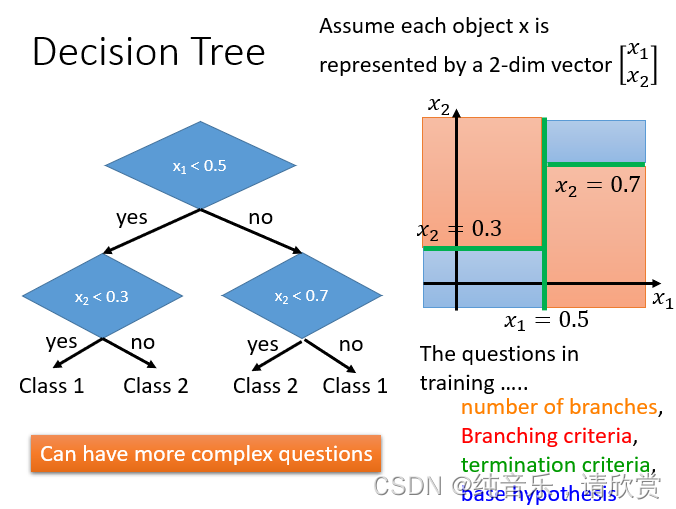
决策树的实际例子：初音问题

描述：输入的特征是二维的，红色的部分是class1，蓝色的部分是class2，其中class1分布的和初音的样子是一样的。我们用决策树对这个问题进行分类。

实验结果

上图可以看到，深度是5的时候效果并不好，图中白色的就是class1，黑色的是class2.当深度是10的时候有一点初音的样子，当深度是15的时候，基本初音的轮廓就出来了，但是一些细节还是很奇怪（比如一些凸起来的边角）当深度是20的时候，就可以完美的把class1和class2的位置区别开来，就可以完美地把初音的样子勾勒出来了。

对于决策树，理想的状况下可以达到错误是0的时候，最极端的就是每一笔data point就是很深的树的一个节点，这样正确率就可以达到100%（树够深，决策树可以做出任何的function）但是决策树很容易过拟合，如果只用决策树一般很难达到好的结果。

用决策树做Bagging就是随机森林。传统的随机森林是通过之前的重采样的方法做，但是得到的结果是每棵树都差不多（效果并不好）。比较多的是随机的限制一些特征或者问题不能用，这样就能保证就算用同样的dataset，每次产生的决策树也会是不一样的，最后把所有的决策树的结果都集合起来，就会得到随机森林。 如果是用Bagging的方法的话，用out-of-bag可以做验证。用这个方法可以不用把label data划分成training set和validation set，一样能得到同样的效果。

强调一点是做Bagging更不会使模型能fit data，所有用深度为5的时候还是不能fit出一个function，所有就是5颗树的一个平均，相当于得到一个比较平滑的树。当深度是10的时候，大致的形状能看出来了，当15的时候效果就还不错，但是细节没那么好，当20 的时候就可以完美的把初音分出来。

决策树

1. Decision Trees (决策树)

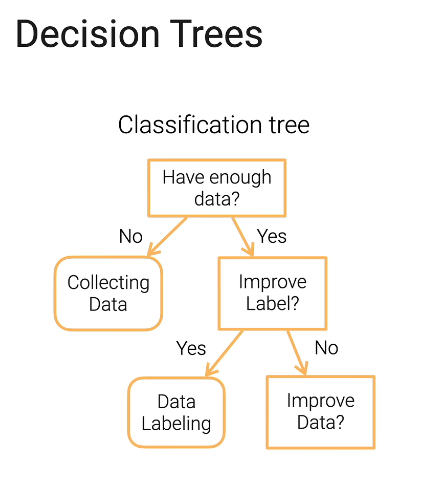
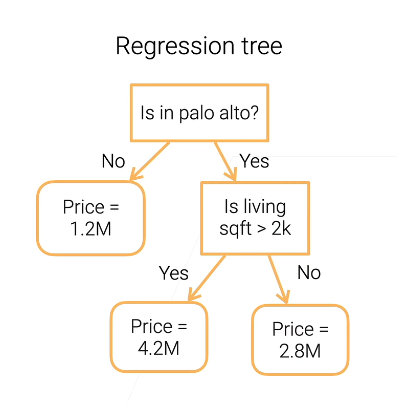
优点

1. Explainable (可解释性)
   叶子结点是什么，一步一步是怎么做下来的，是机器学习为数不多的可以用来给大家介解释的模型
   
   

2. Can handle both numerical and categorical features （数值与分类特征）
   缺点

Very non-robust(unsemble to help) （鲁棒性很底）

complex trees cause overfitting(prune trees) （复杂的树容易过拟合）

not easy to be parallelized in computing （很难并行）

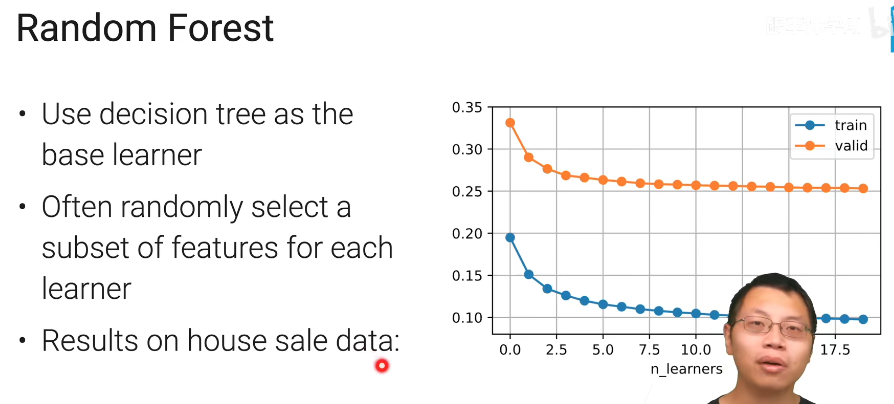
2. Random Forest (随机森林)

1. 一棵树不稳定，有很多办法让他变得稳定，最常见的办法是随机森林
2. 
   就是他是一个随机产生的树
   
   e.g. 【1，2，3，4，5】 -》【1,2,2,3,4】

随机森林就是用决策树做我的baselearner


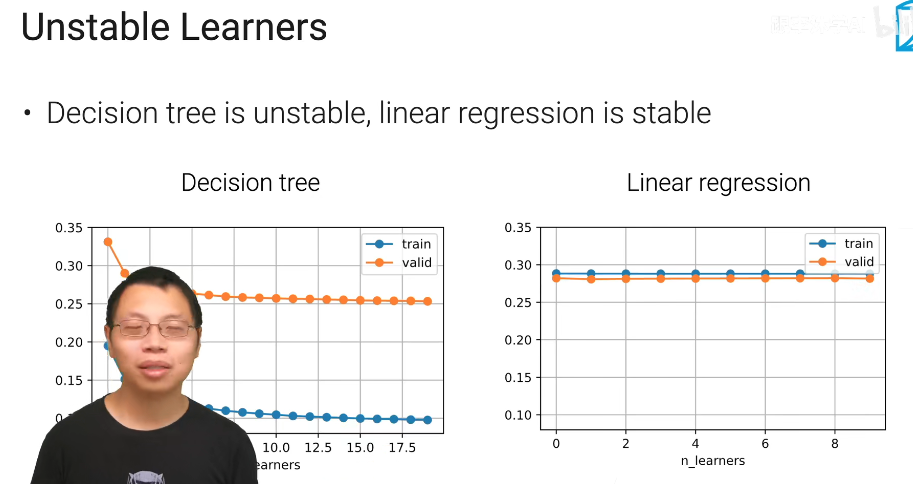
什么时候会变好，什么时候不会更好？

线性回归比较稳定

3. Gradient Boosting Decision Trees(梯度提升决策树)

Boosting

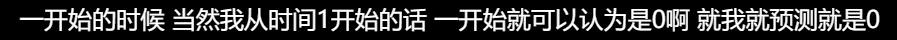
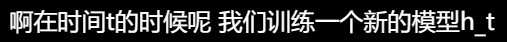
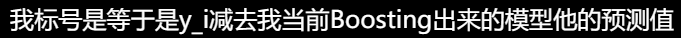
假设我们这里做回归

减少过拟合：1. 弱模型（决策树少层，抽取特征） 2. 学习率

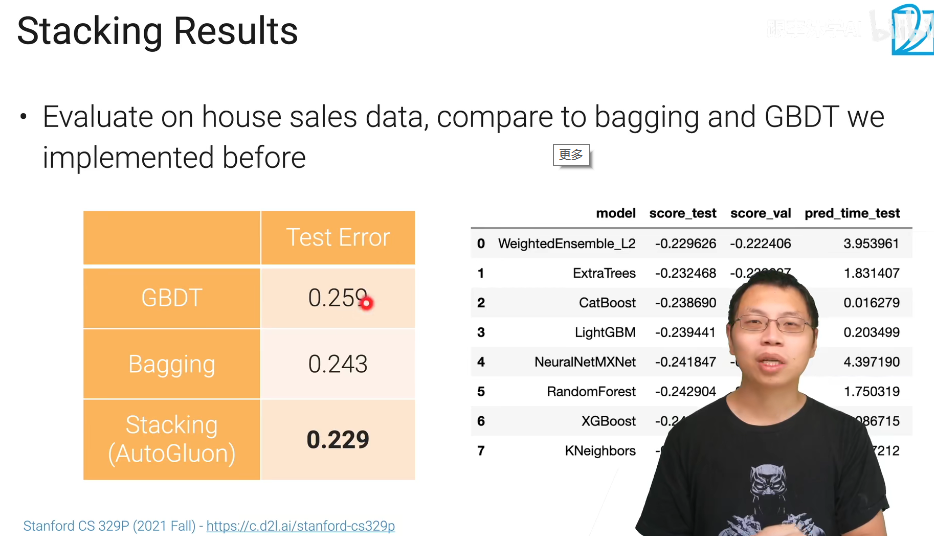
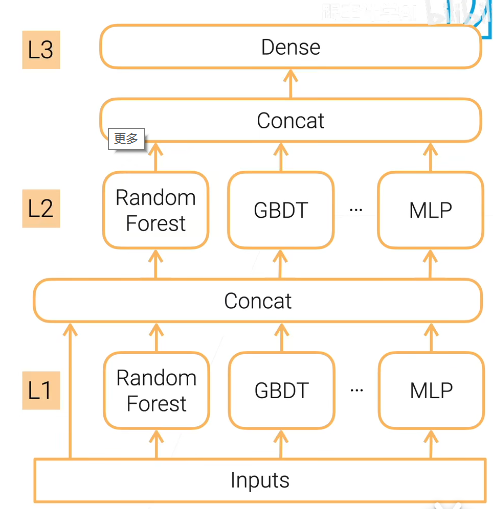
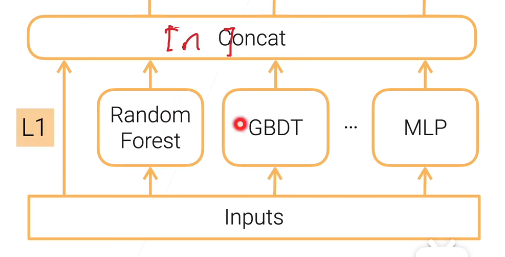
Stacking

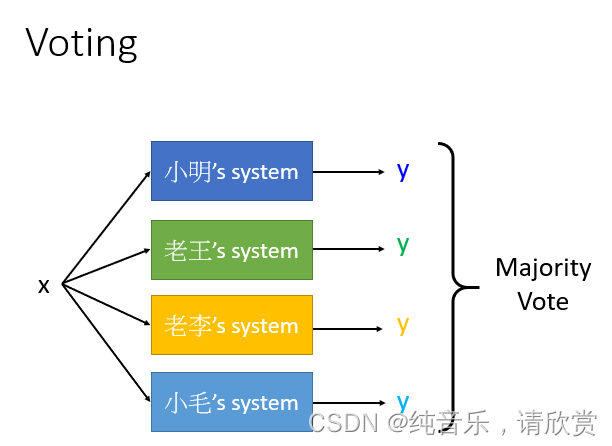
上图中，把一笔数据x输入到四个不同的模型中，然后每个模型输出一个y，然后用投票法决定出最好的（对于分类问题）

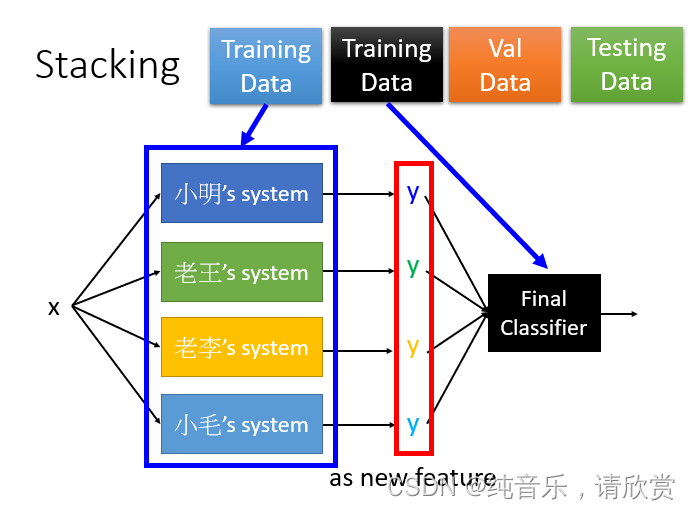
但是有个问题就是并不是所有系统都是好的，有些系统会比较差，但是如果采用之前的设置低权重的方法又会伤害小毛的自尊心，这样我们就提出一种新的方法： 把得到的y当做新的特征输入到一个最终的分类器中，然后再决定最终的结果。 对于这个最终的分类器，应当采用比较简单的函数（比如说逻辑回归），不需要再采用很复杂的函数，因为输入的y已经训练过了。

在做stacking的时候我们需要把训练数据集再分成两部分，一部分拿来学习最开始的那些模型，另外一部分的训练数据集拿来学习最终的分类器。原因是有些前面的分类器只是单纯去拟合training data，比如小明的代码可能是乱写的，他的分类器就是很差的，他做的只是单纯输出原来训练数据集的标签，但是根本没有训练。如果还用一模一样的训练数据去训练最终分类器，这个分类器就会考虑小明系统的功能。所以我们必须要用另外一部分的数据来训练最终的分类器，然后最终的分类器就会给之前的模型不同的权重。

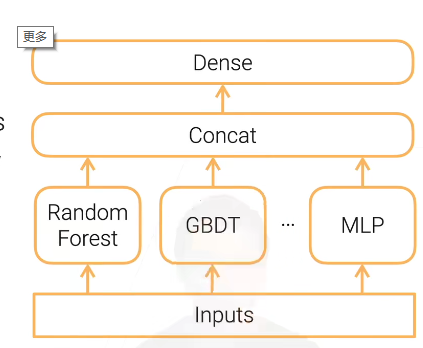
SVM

课程链接

支持向量机要解决的问题

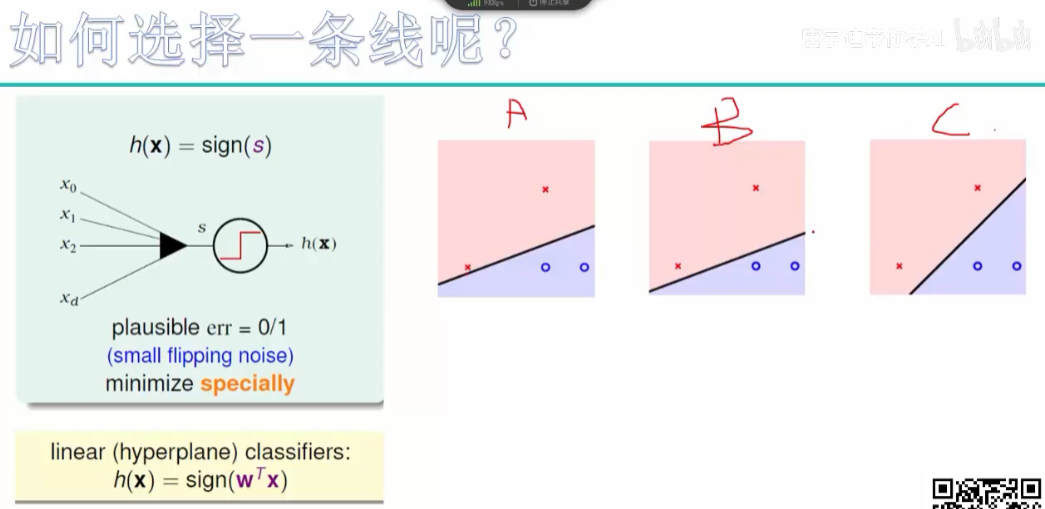
数据本身是二维的，怎么在更高维度分？

SVM的基本原理？：

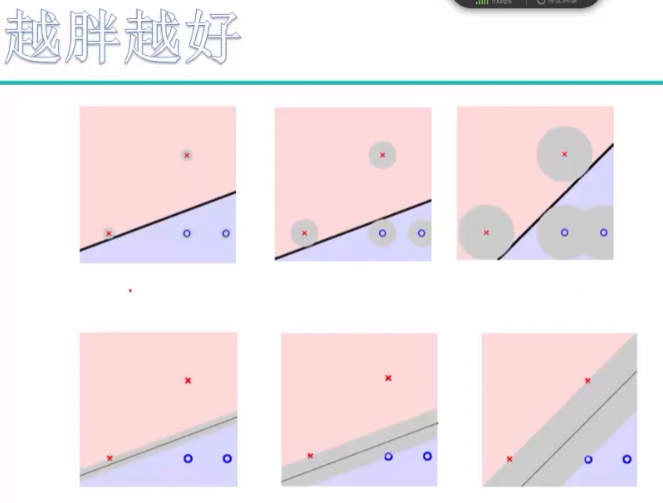
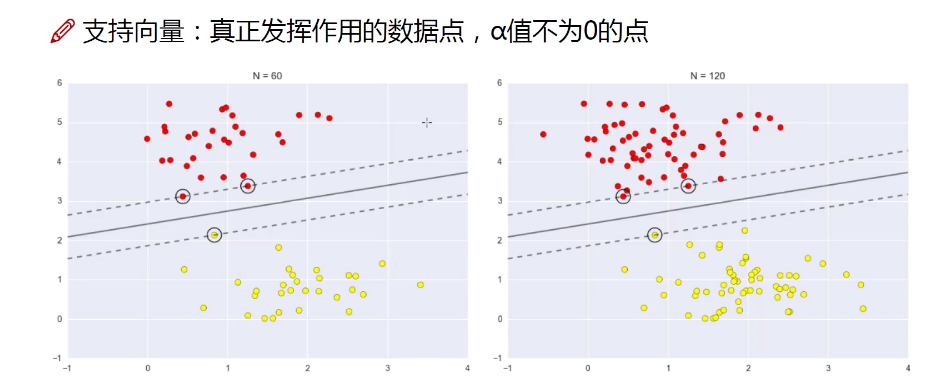
支持向量机为一个二分类模型，SVM的目标是寻找一个最优的分离超平面，将两类数据在空间中分离开来，并且使得这个超平面到最近的点的间隔最大，这些点称为支持向量。

距离和数据定义

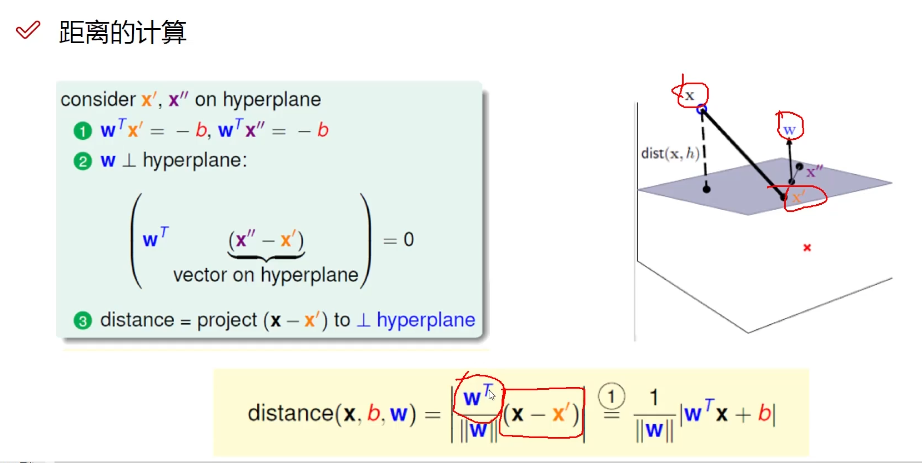
目标函数推导

拉格朗日乘子法求解

要求w需要先求alpha

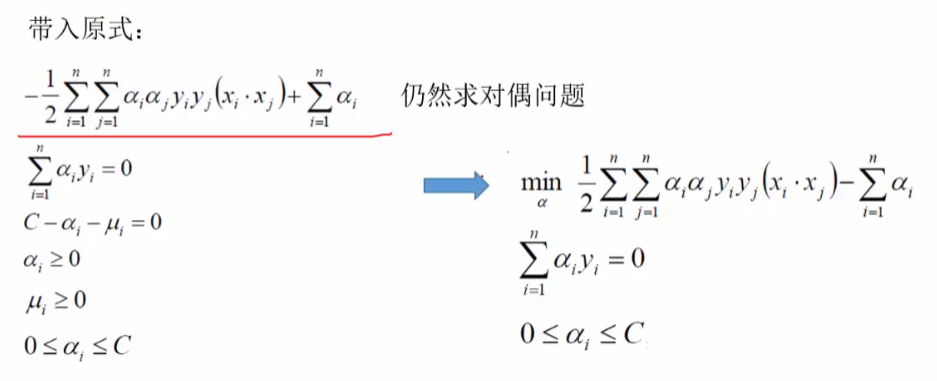
引入对偶算法的优点？

1. 一是对偶问题往往更容易求解。当我们寻找约束存在时的最优点的时候，约束的存在虽然减小了需要搜寻的范围，但是却使问题变得更加复杂。为了使问题变得易于处理，我们的方法是把目标函数和约束全部融入一个新的函数，即拉格朗日函数，再通过这个函数来寻找最优点；
2. 二是方便引入核函数，（因为对偶问题涉及的是数据的内积计算）进而推广到非线性分类问题。

化简最终目标函数

序列最小优化算法（Sequential minimal optimization, SMO）是一种用于解决支持向量机训练过程中所产生优化问题的算法。

求解决策方程

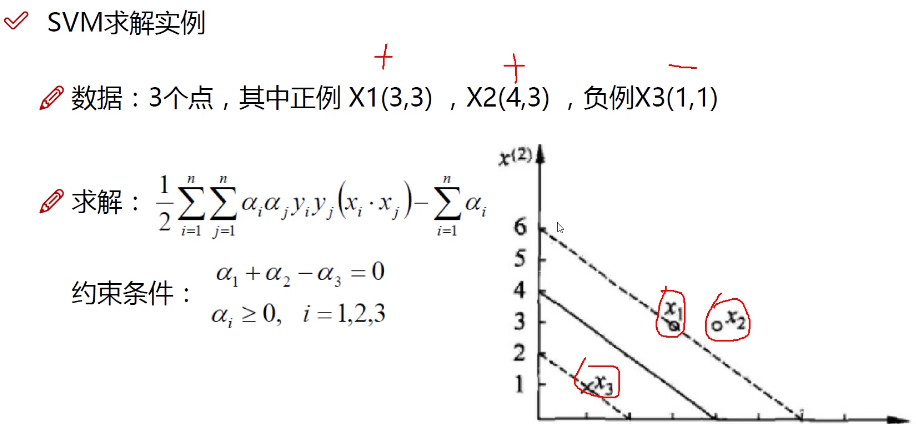
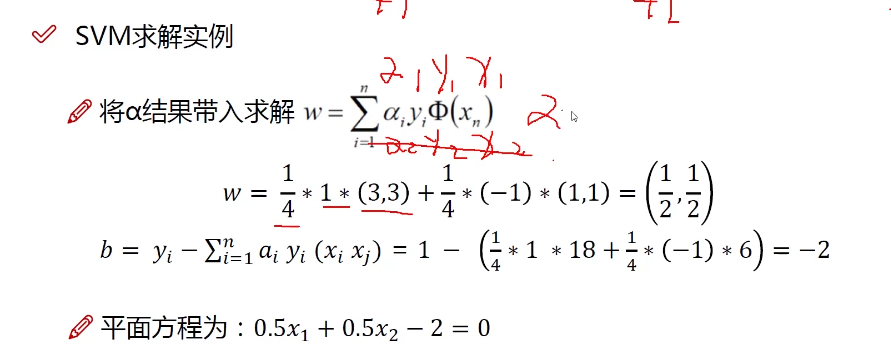
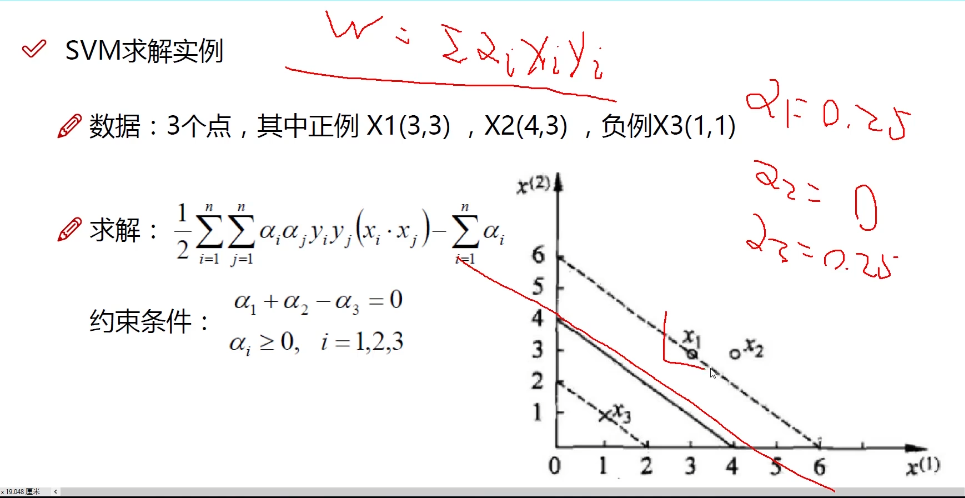
alphe2为0，x2不起作用

软间隔优化

原先支持向量机在分对的情况下（y*y(x) > 0）才考虑最大间隔，

核函数的作用

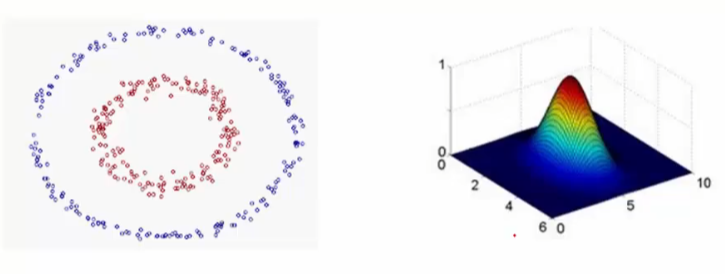
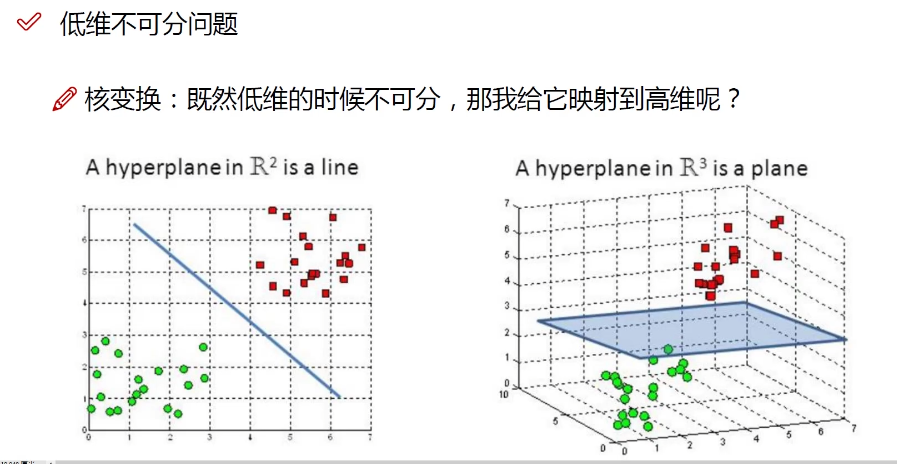
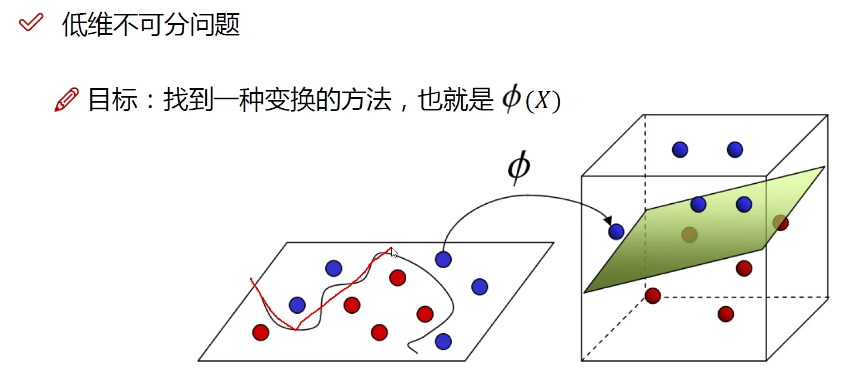
也可以就在低维度解决问题，但是过拟合的风险比较大

利用数学上的这种巧合来完成这件事

想要找到一个合适的核函数，就是低维空间的内积映射到高维空间中等于先映射到高维空间再求内积，满足条件的并没有几个

最常用的：

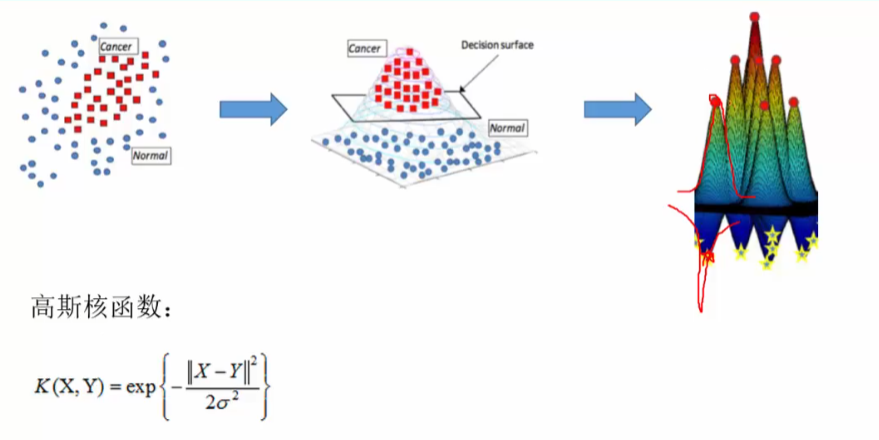
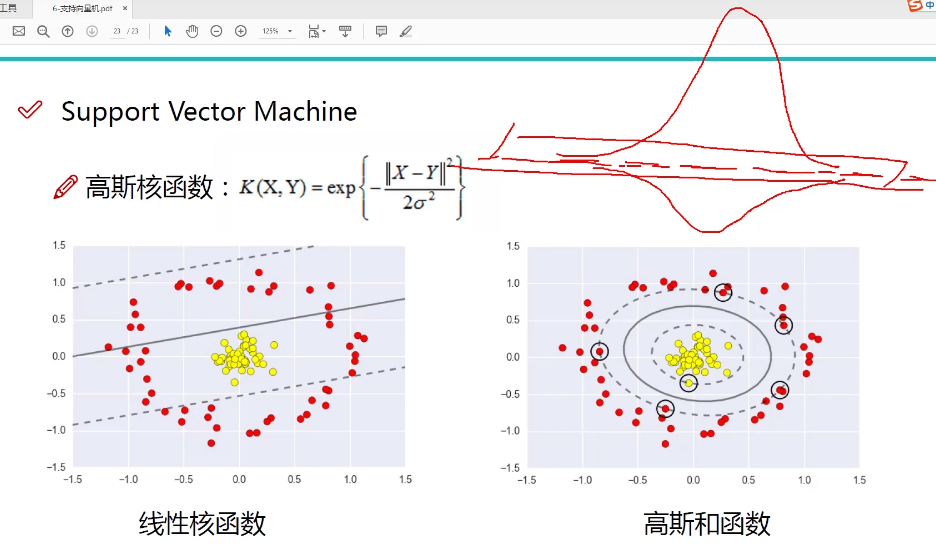
理解：吧原始的特征映射到高斯核函数中的距离特征

非线性SVM

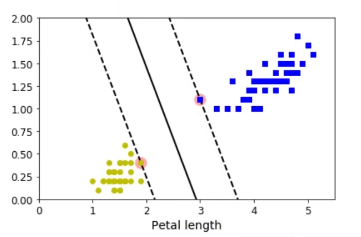
尽管SVM分类器非常高效，并且在很多场景下都非常实用。但是很多数据集并不是可以线性可分的。一个处理非线性数据集的方法是增加更多的特征，例如多项式特征。在某些情况下，这样可以让数据集变成线性可分。下面我们看看下图左边那个图：

它展示了一个简单的数据集，只有一个特征x1，这个数据集一看就知道不是线性可分。但是如果我们增加一个特征x2 = (x1)2，则这个2维数据集便成为了一个完美的线性可分。

多项式核（Polynomial Kernel）

增加多项式特征的办法易于实现，并且非常适用于所有的机器学习算法（不仅仅是SVM）。但是如果多项式的次数较低的话，则无法处理非常复杂的数据集；而如果太高的话，会创建出非常多的特征，让模型速度变慢。

不过在使用SVM时，我们可以使用一个非常神奇的数学技巧，称为核方法（kernel trick）。它可以在不添加额外的多项式属性的情况下，实现与之一样的效果。这个方法在SVC类中实现，下面我们还是在moons 数据集上进行测试：

from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
    ('scalar', StandardScaler()),
    ('svm_clf', SVC(kernel='poly', degree=3, coef0=1, C=5))
])

poly_kernel_svm_clf.fit(X, y)
1
2
3
4
5
6
7
8

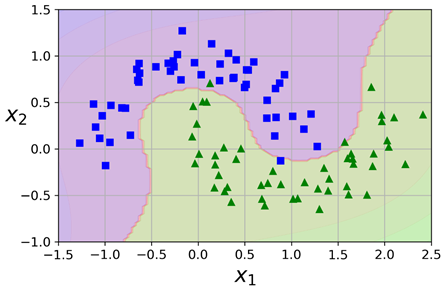
上面的代码会使用一个3阶多项式核训练一个SVM分类器，如下面的左图所示：

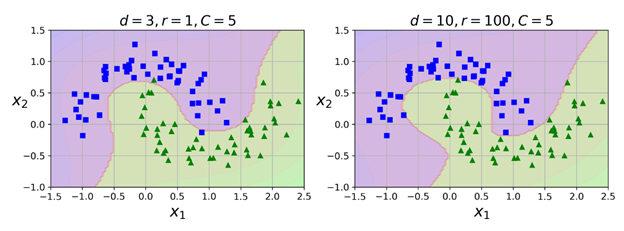
右图是另一个SVM分类器，使用的是10阶多项式核。很明显，如果模型存在过拟合的现象，则可以减少多项式的阶。反之，如果欠拟合，则可以尝试增加它的阶。超参数coef0 控制的是多项式特征如何影响模型。

SVR支持向量回归

支持向量机(SVM)本身是针对二分类问题提出的，而SVR（支持向量回归）是SVM（支持向量机）中的一个重要的应用分支。SVR回归与SVM分类的区别在于，SVR的样本点最终只有一类，它所寻求的最优超平面不是SVM那样使两类或多类样本点分的“最开”，而是使所有的样本点离着超平面的总偏差最小。

1. SVM是要使到超平面最近的样本点的“距离”最大；

2. SVR则是要使到超平面最远的样本点的“距离”最小。
   

决策树

【数据挖掘】决策树零基础入门教程，手把手教你学决策树！

什么是决策树

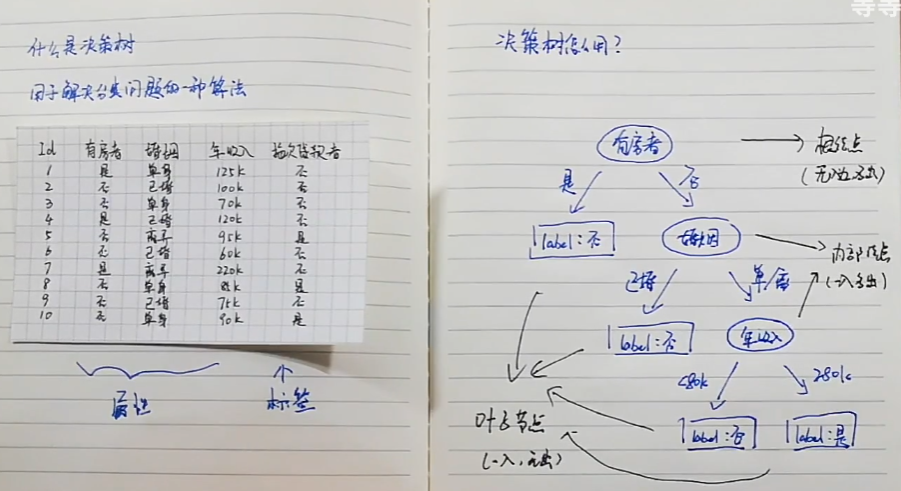
构建决策树

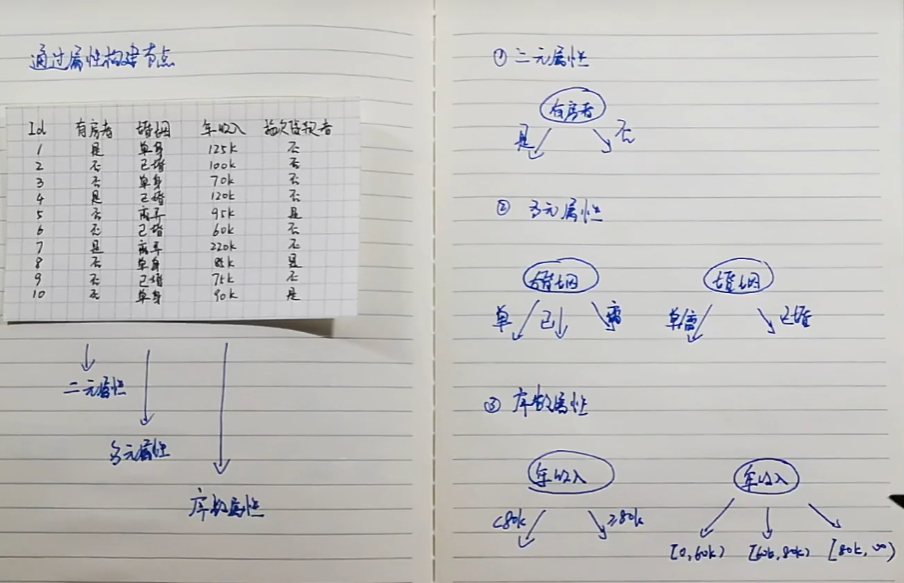
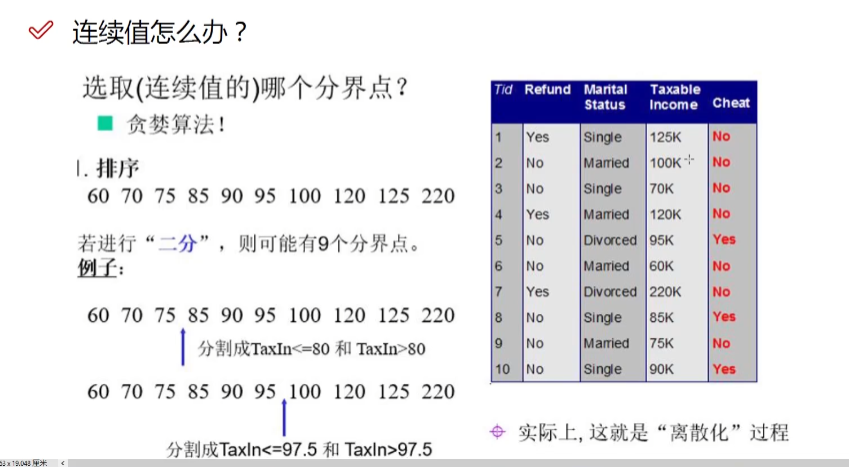
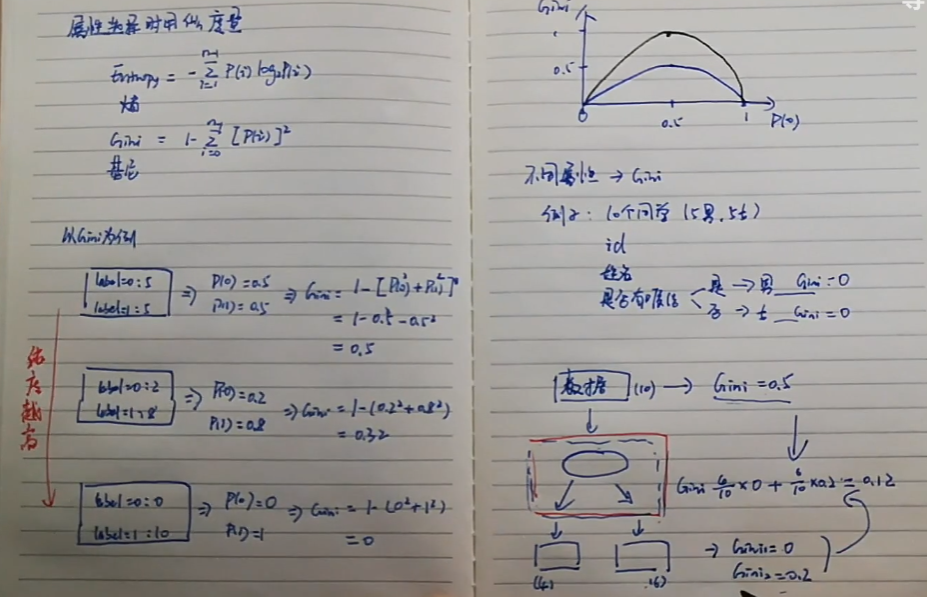
信息增益的问题：
不适合解决ID这种特别稀疏的特征

模型评估

Evaluation Metrics

1. Model Metrics

1. Supervised learning : 使用训练误差作为一个简单地评估标准

2. other metrics:

2.1 model specific : e.g. accuracy for classification ,mAP （分类的精度、召回）
2.2 buisness specific : e.g. revenue,inference latency（商业例子中需要很多的评估指标，进行不同的综合）

2. Metrics for Classification

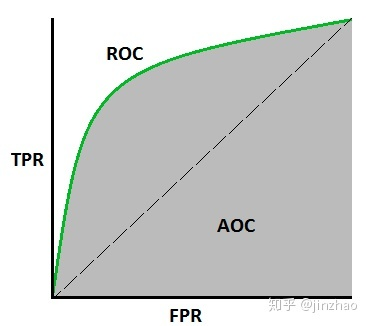
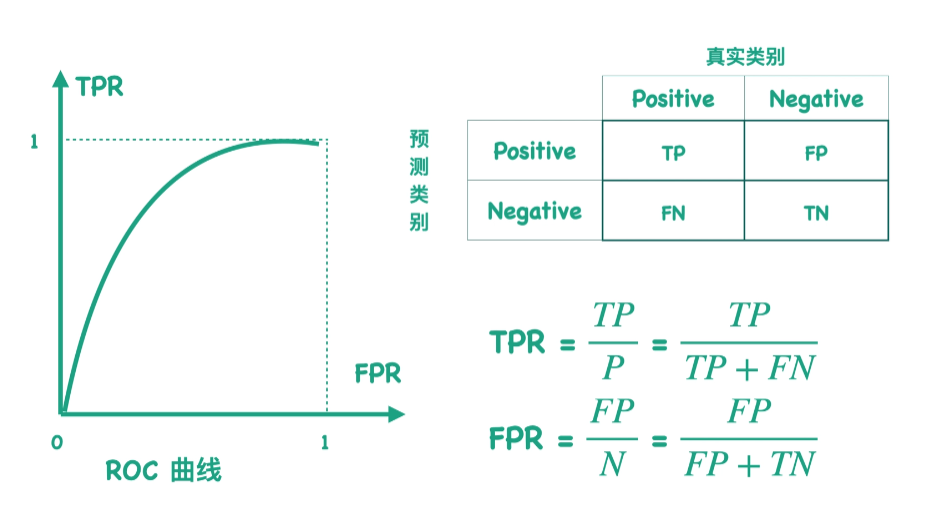
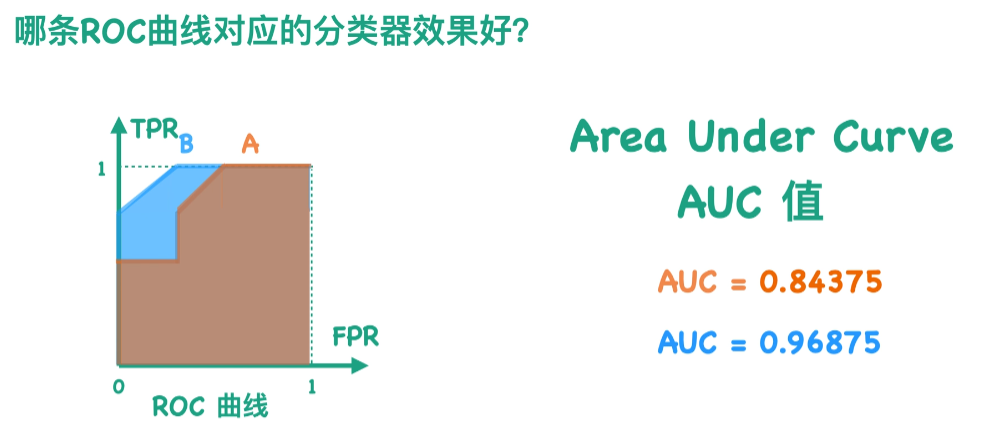
3. AUC & ROC

AUC : ROC曲线下面的面积

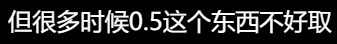
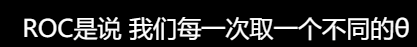
1. 理想情况下，两条曲线完全不重叠时，模型可以将正类和负类别完全分开
   

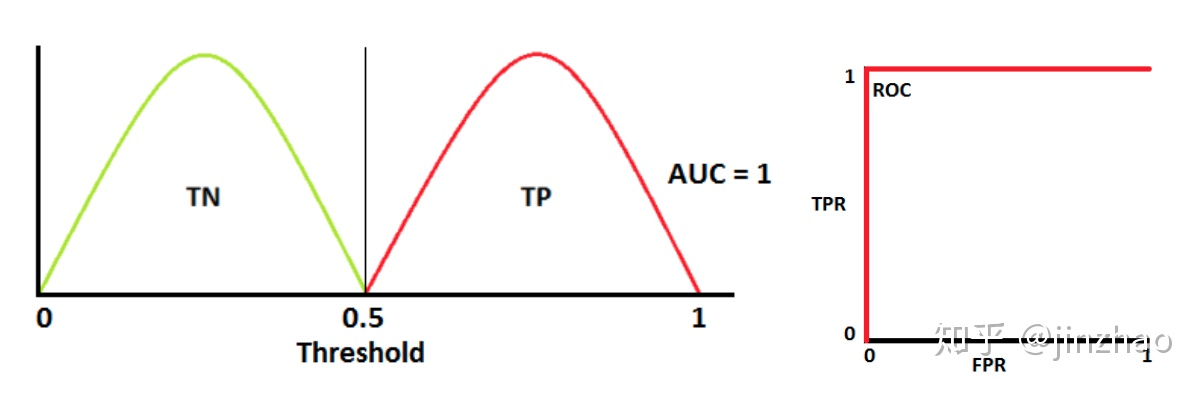
2. 两个部分重叠时，根据阈值，可以最大化和最小化概率，当AUC=0.7时，表示模型有70%的概率能够区分negtive和positive类别
   

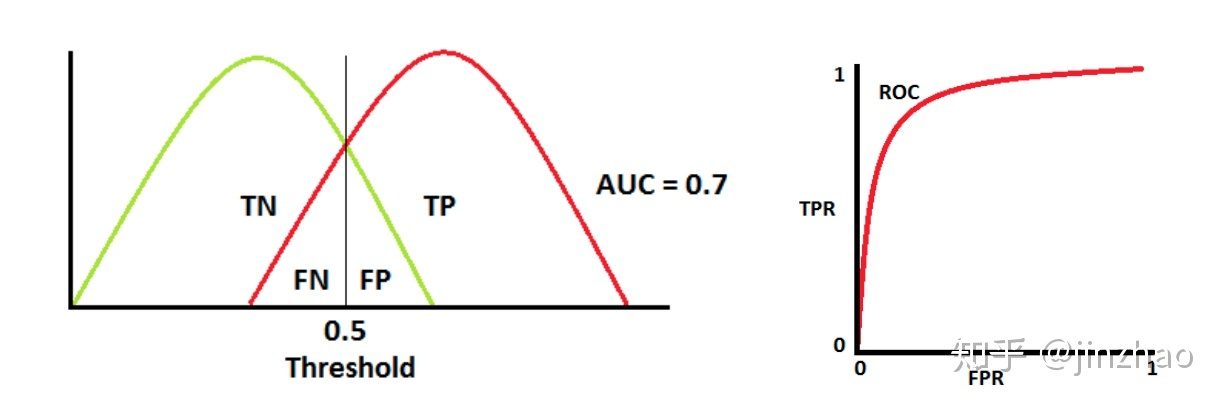
3. 当AUC =0.5 时，表示模型将判断negtive 类和positive的概率相等
   

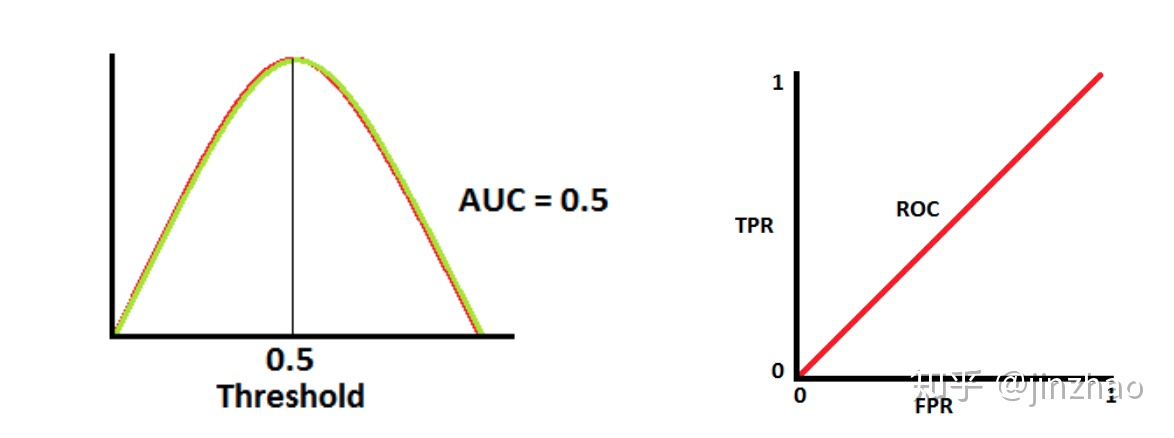
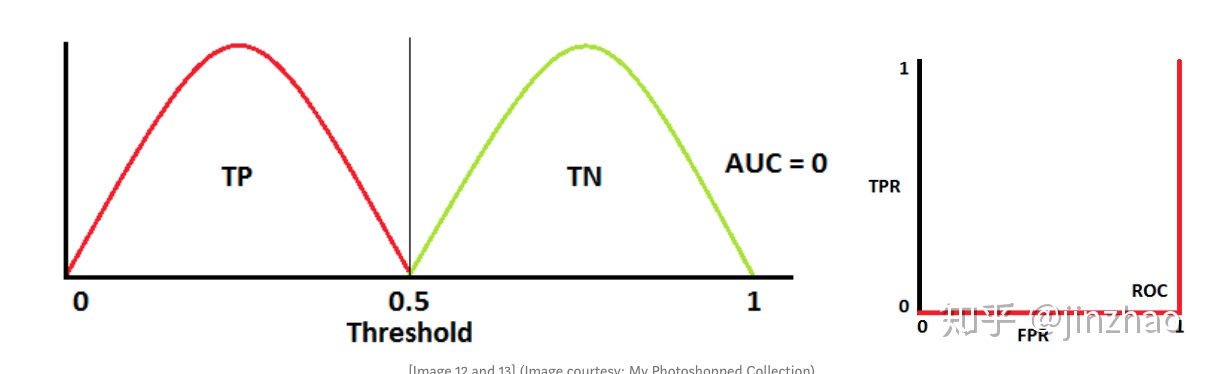
4. 当AUC =0 时，表示模型将negtive 类预测为positive，反之亦然。（并非坏事）

什么时候使用ROC-AUC

1. 关心的是对于排名的预测，而不需要输出经过良好校准的概率。
2. 样本不均衡
3. 同样关心Positive samples 和 Negative samples

版本2
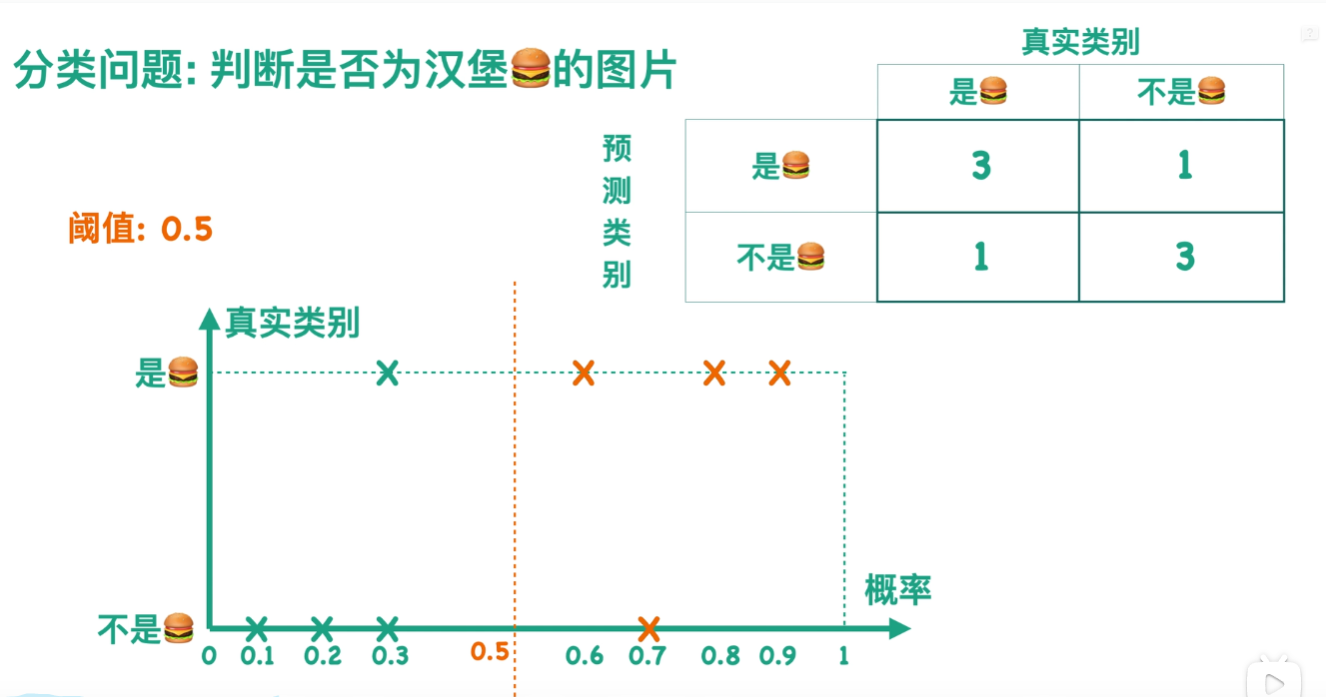
阈值为0.5：

阈值为0-1任意

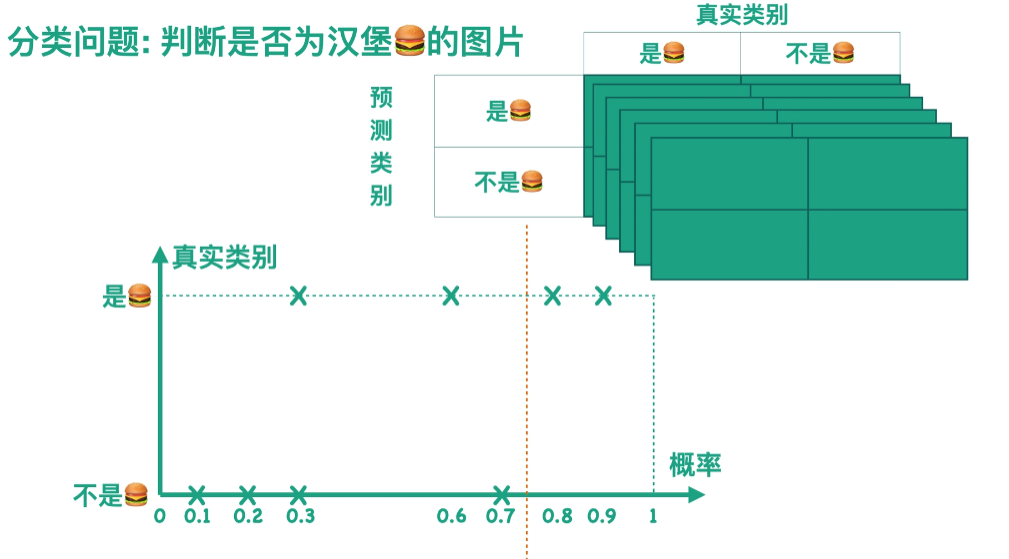
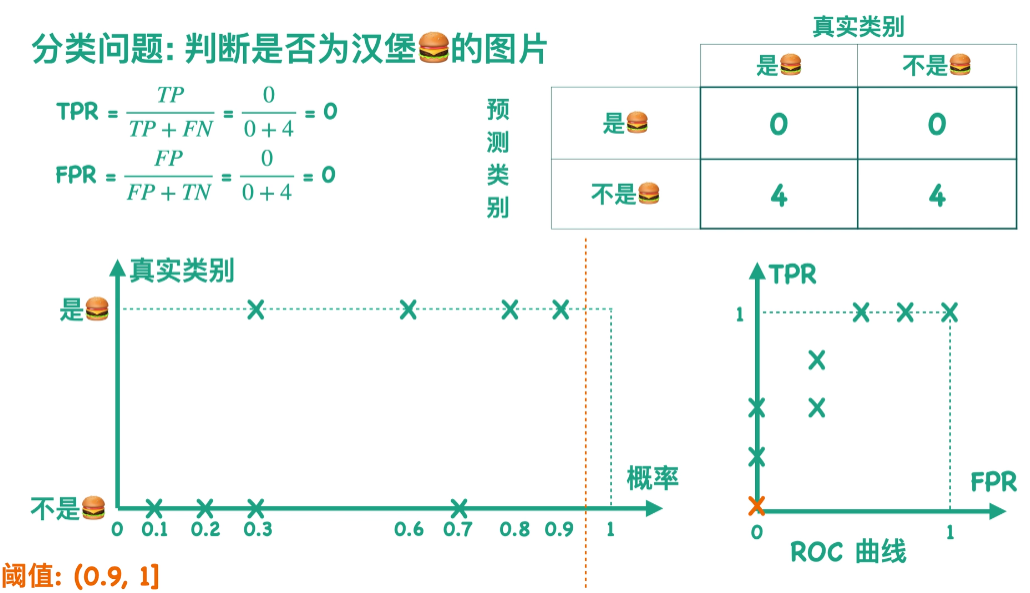
FPR越小越好，TPR越大越好

交叉熵

直观理解信息量和信息熵的含义

信息的作用是消除不确定性。
一句话的信息量和它能消除的不确定性有关。

比如掷骰子，猜点数。

和朋友玩一个小游戏。猜小球的数字。你可以问他问题，他只能回答你yes no。为了体现信息的价值，每问一次问题都需要支付朋友1元钱。

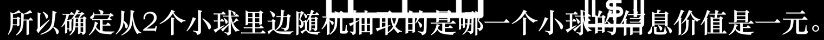
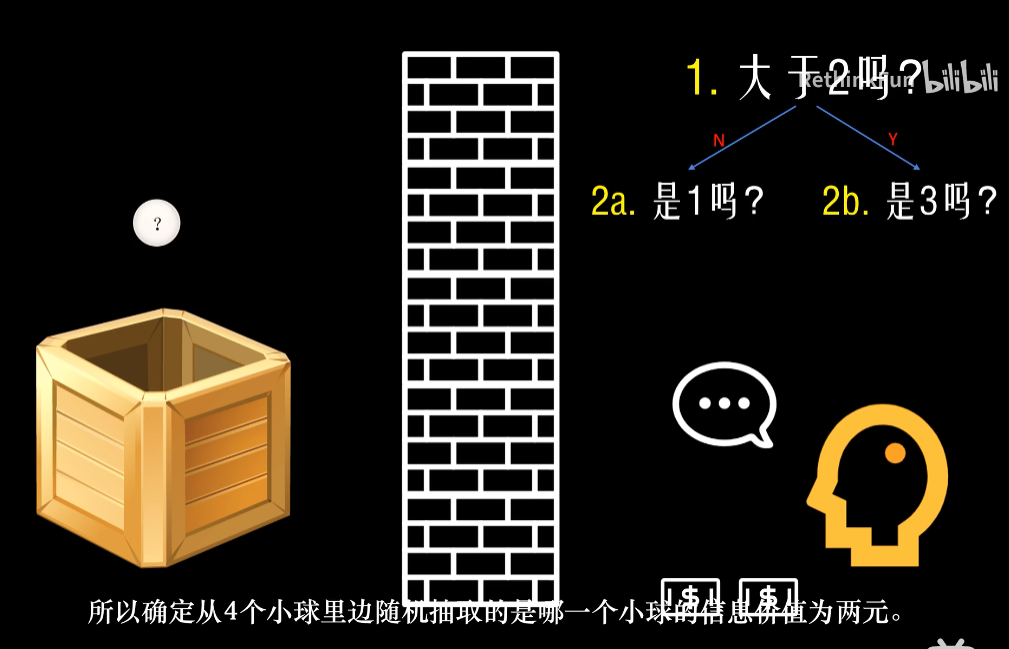
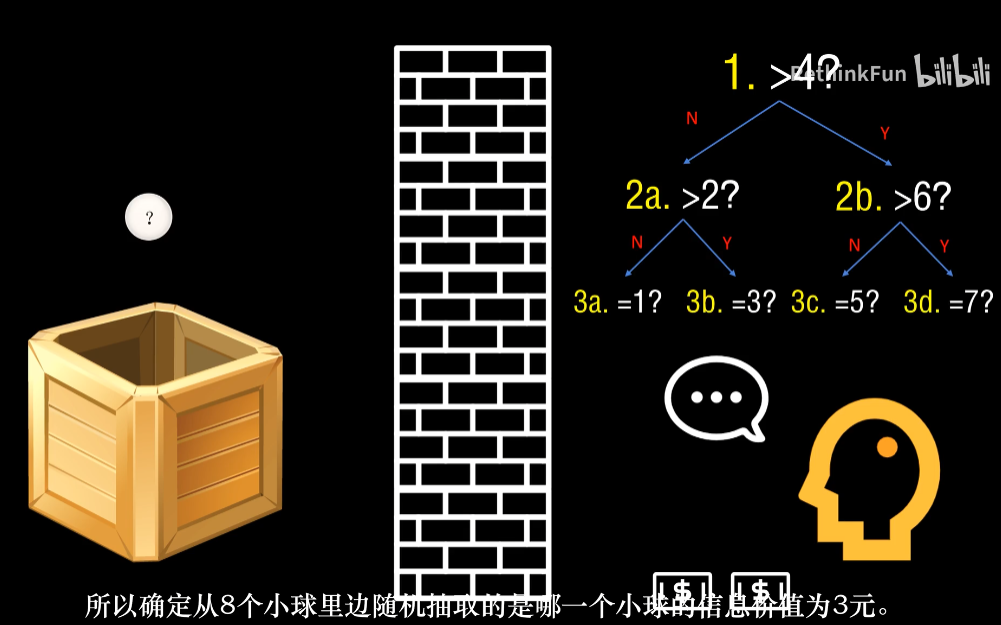
由摸小球的概率理解信息熵。

可以设定每个小球被摸到的概率。并且每次摸球的结果以邮件告知。

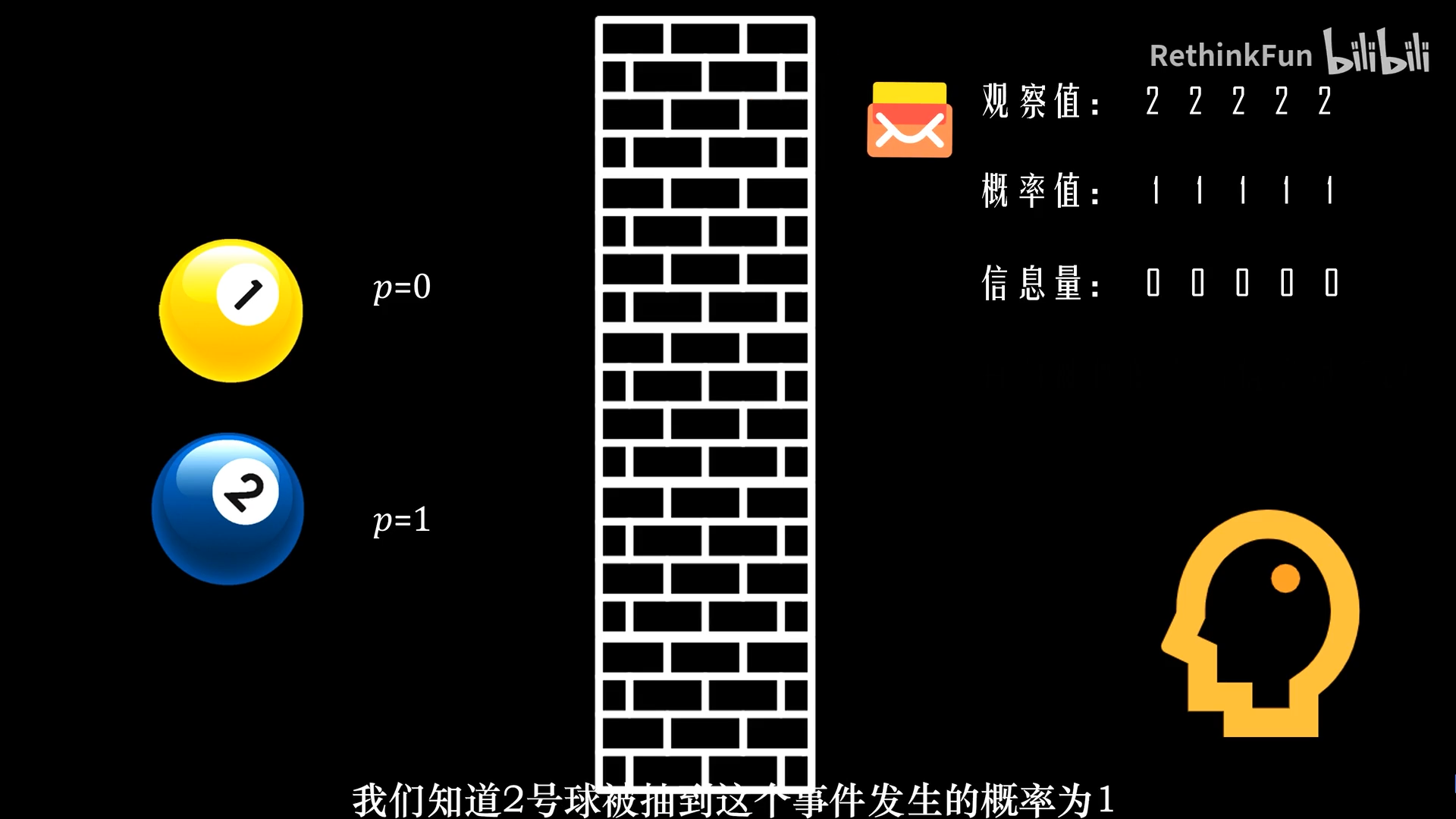
第一回，摸了5次球，发了5封邮件告知摸球的结果。如上图。

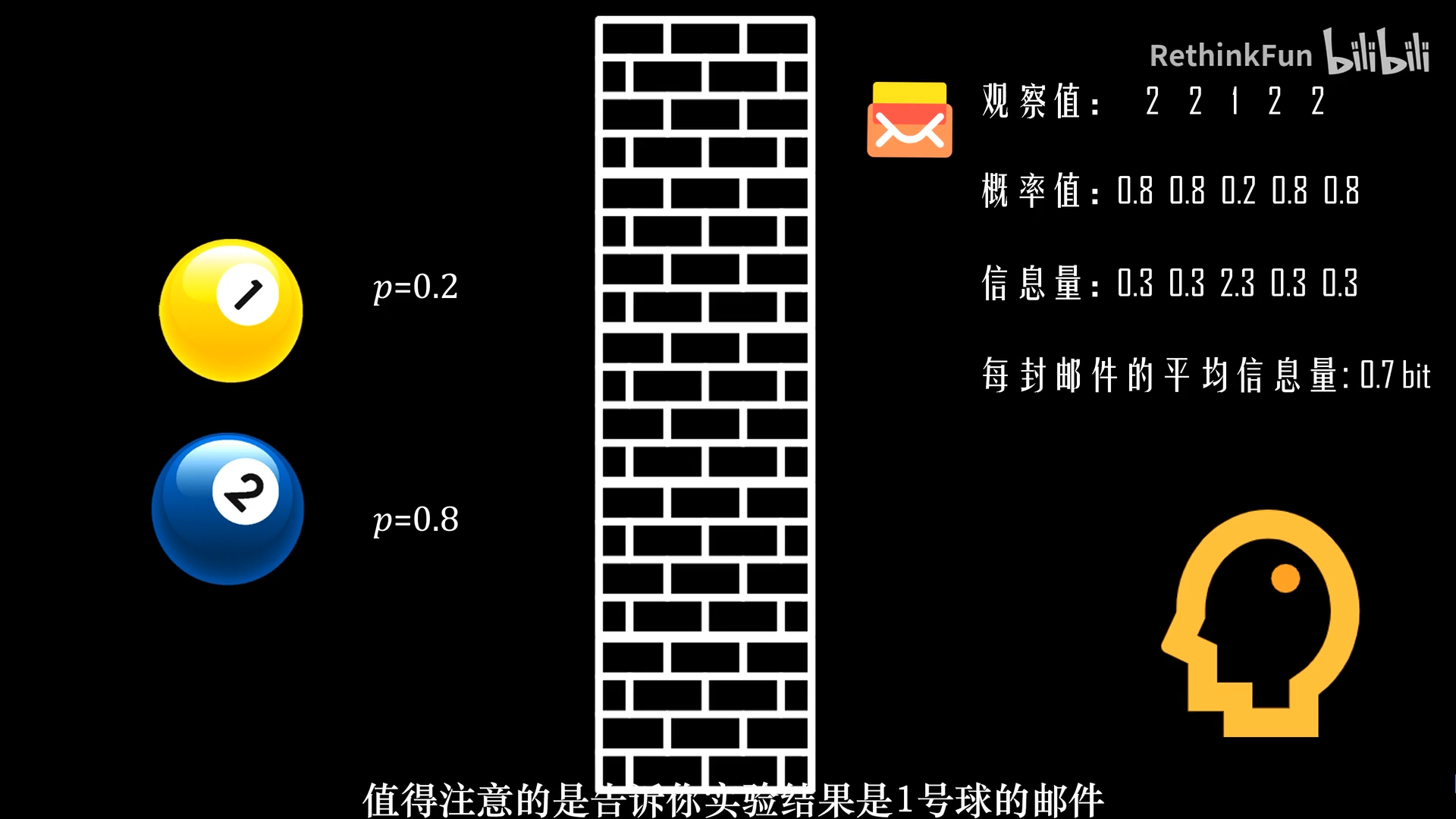
小概率事件发生的信息量特别大。

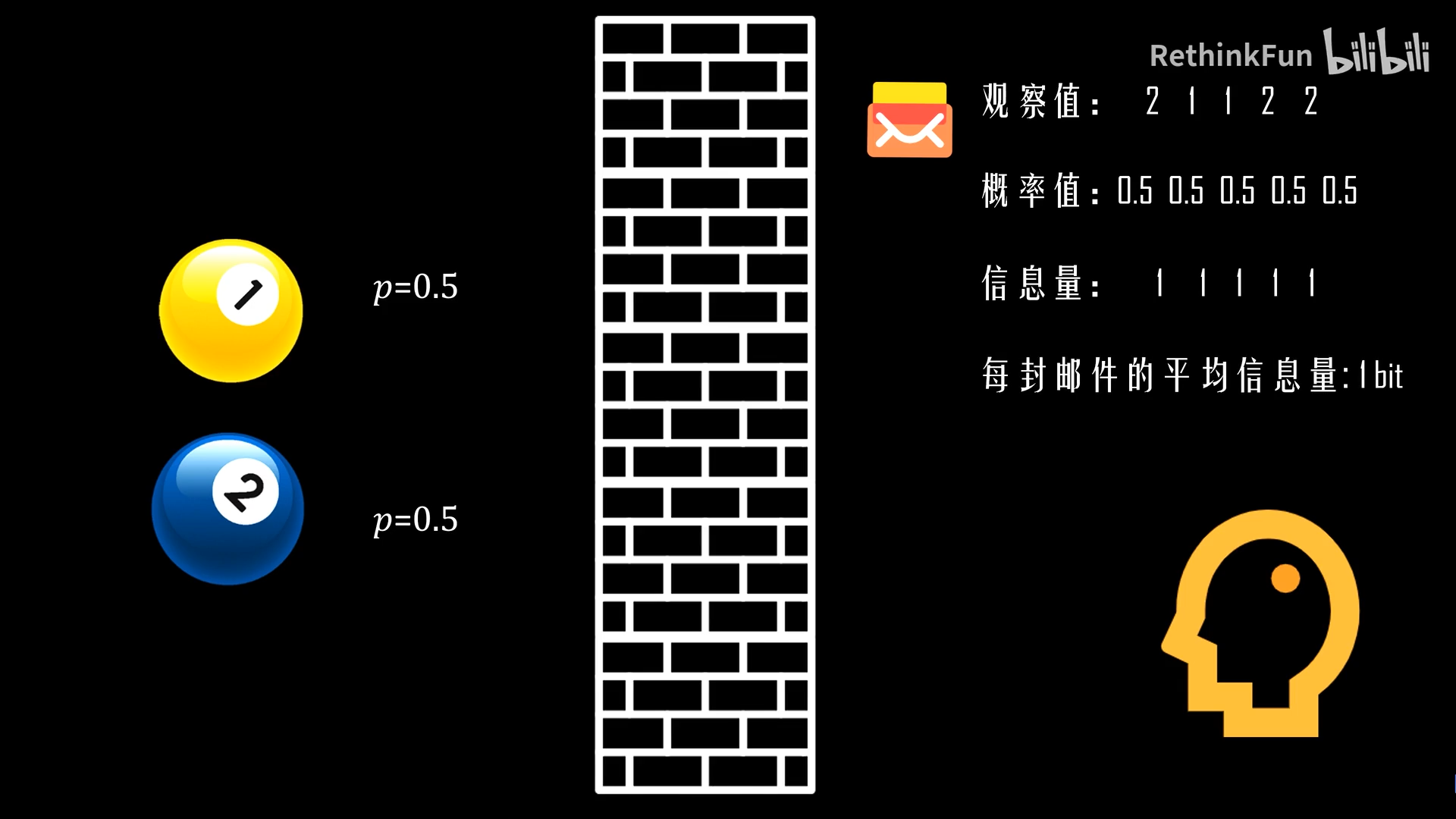
1. 这里的邮件平均信息量就是信息熵。它描述的是一个系统内发生一个事件时，这个事件能给你带来的信息量的期望。

2. 信息熵的公式就是这个系统内所有事件发生时提供的信息量与它发生概率的乘积进行累加。

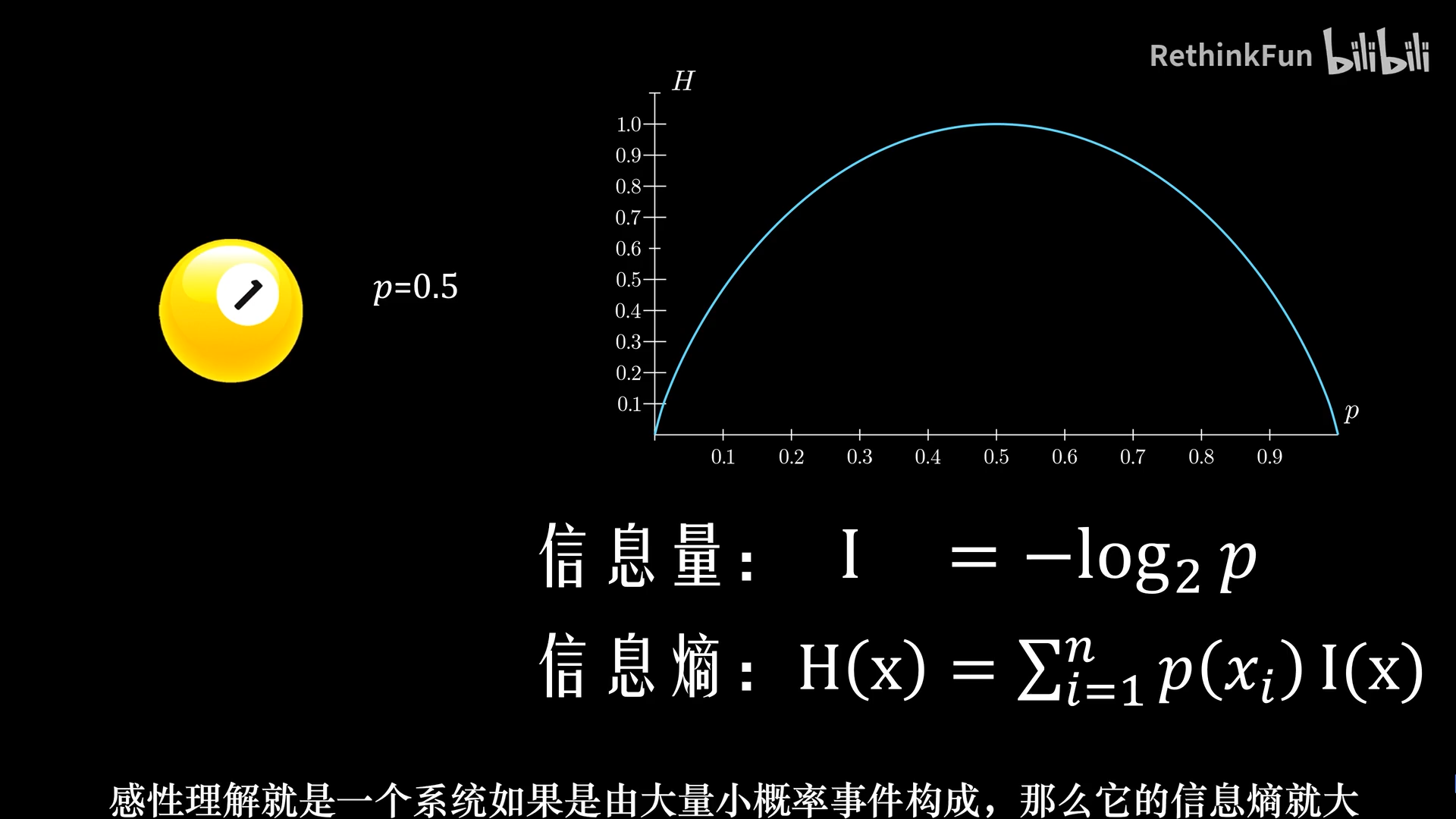
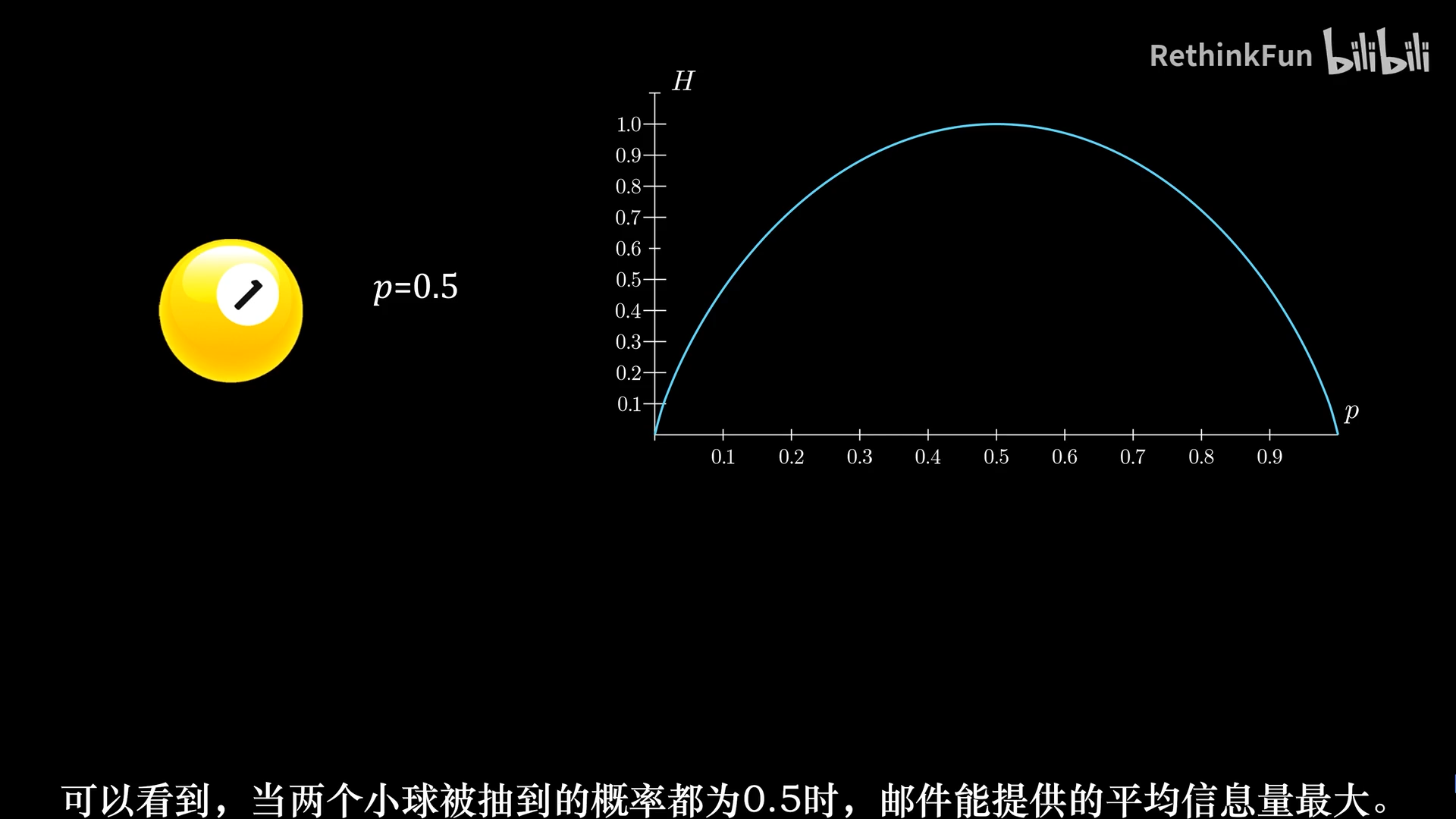
感性理解就是，一个系统如果是由大量小概率事件构成，那么它的信息熵就大。信息熵描述的是一个系统的复杂或者混乱程度，这一点和热力学里的熵是一致的。

交叉熵损失函数

交叉熵的定义：

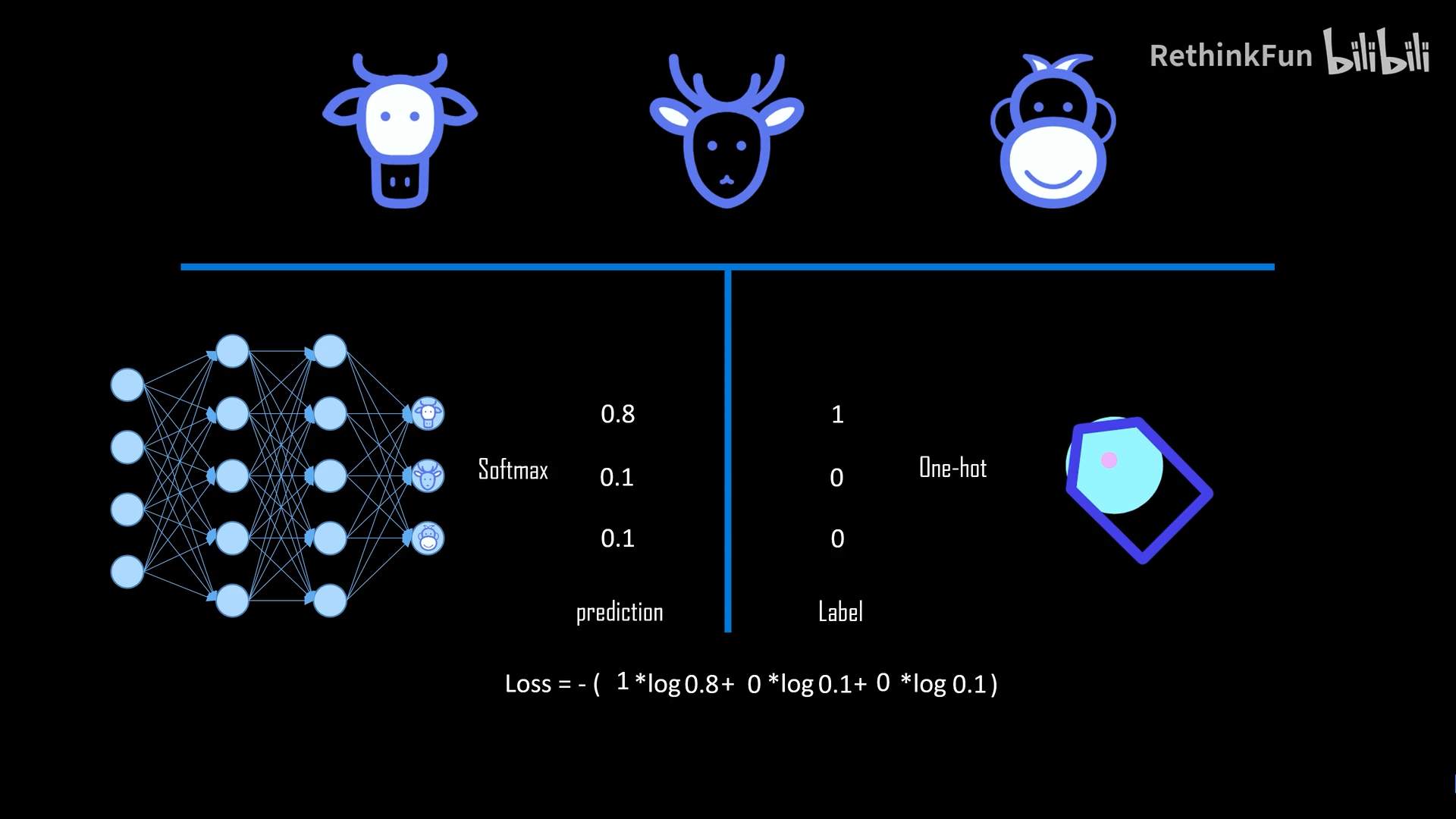
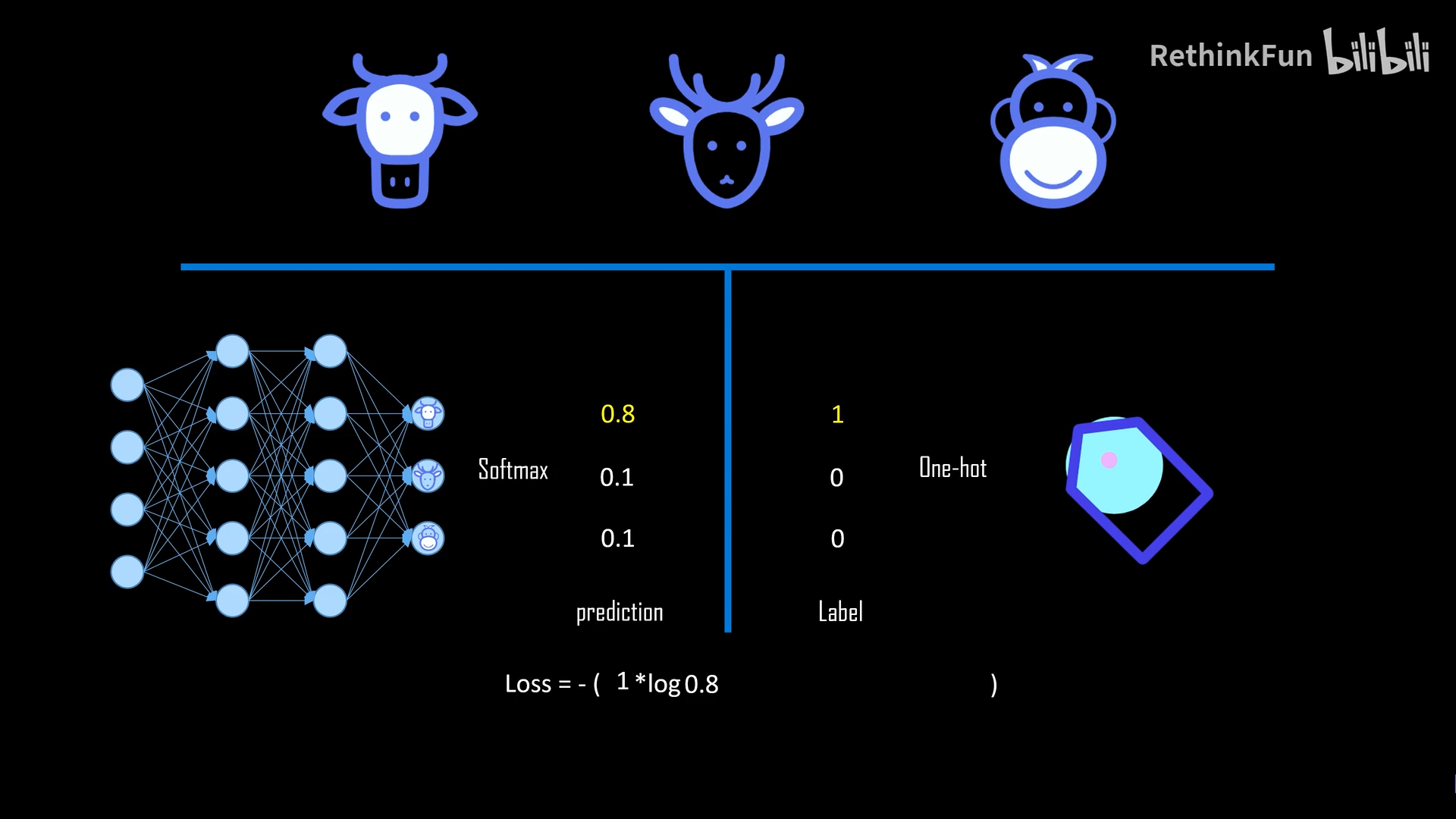
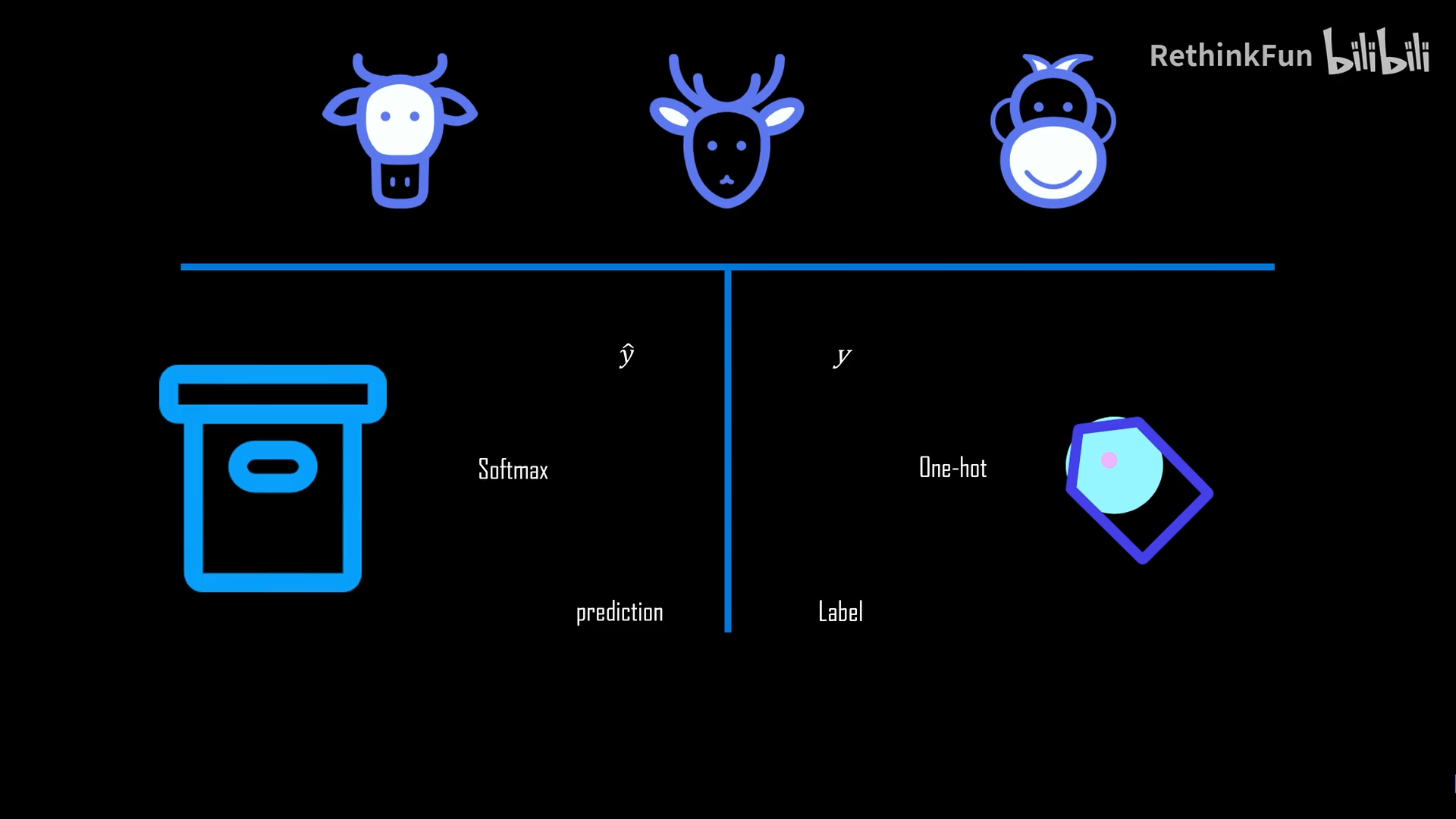
极大似然估计法的定义

在一个黑箱里有放回地摸10次球，摸到8次白球，2次黄球。估计箱内白球的占比。把出现白球的概率设置为p，出现黄球的概率设置为1-p.

让出现该实验结果的概率最高，也就是找使得(p^8)[(1-p)2]最大的p，且p在（0，1）之内。

通过求导，得p=0.8。

从负对数似然的角度来理解交叉熵

1. 神经网络可以看做一个黑盒，每个类别输出是一个概率。label是实验的观测值。每个样本可以看做一次独立抽样。在所有的样本上，让模型输出和label一样值的概率最大。也就得到了最优模型。

2. 如何计算一次抽样模型预测正确的概率？它就等于每个类别预测概率的one-hot encoding的次方的累乘。因为one-hot encoding在非真类别上为0，真实类别上为1。而且任何数的0次方为1，任何数的1次方为自身。
   

从信息论的角度来理解交叉熵

1. 引入一个结论：一个系统的信息熵是对这个系统平均最小的编码长度。

比如一个地区有4种天气，分别是阴晴雨雪。

1. 上面这个例子让你直观理解一个系统的信息熵是对这个系统平均最小的编码长度，如果采样其他的编码形式，那么肯定编码长度是要大于信息熵编码的
2. 交叉熵损失函数就是利用这个特性来衡量其他编码格式和信息熵编码格式之间的编码长度的差距，换句话说，就是利用信息熵的最短编码特性来评估一个样本在不同类别上的真实概率分布和预测概率分布之间的差值

如果预测值y帽的概率和真实值y的概率一致，那么久退化成了信息熵公式，我们得到的交叉熵损失就为最小值；否则就还有优化的空间

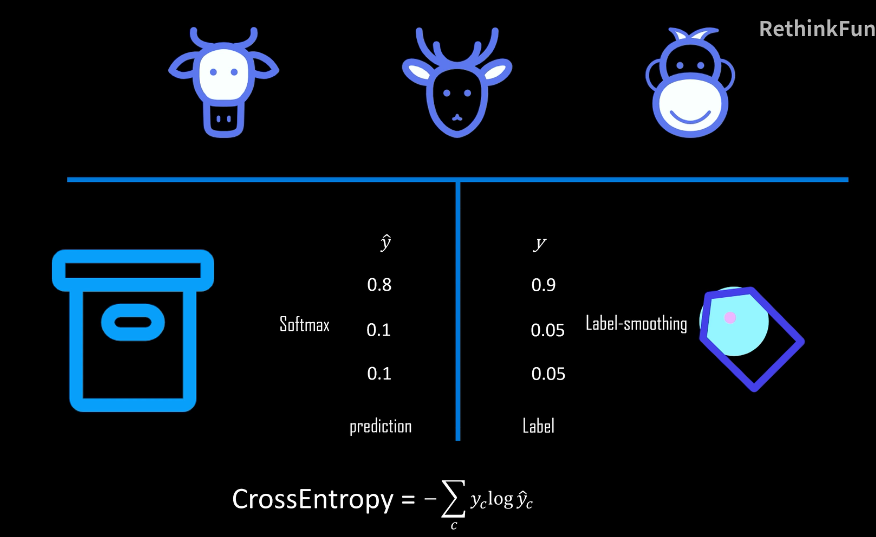
KL散度 = 交叉熵 - 熵

1. 熵(Entropy)

抽象解释：熵用于计算一个随机变量的信息量。对于 一个随机变量X，X的熵就是它的信息量，也就是它的不确定性。

熵的数学定义为：

从编码的角度理解熵
对于任意一个离散型随机变量，我们都可以对其进行编码。例如我们可以把字符看出一个离散型随机变量。
根据shannon的信息论，给定一个字符集的概率分布，我们可以设计一种编码，使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X，对x∈X，其出现概率为P(x)，那么其最优编码（哈夫曼编码）平均需要的比特数等于这个字符集的熵。

2. KL散度(Kullback-Leibler divergence)

抽象解释：KL散度用于计算两个随机变量的差异程度。相对于随机变量X，随机变量Y有多大的不同？这个不同的程度就是KL散度。KL散度又称为信息增益，相对熵。需要注意的是KL散度是不对称的，就是说：X关于Y的KL散度 不等于 Y关于X的KL散度。

形象例子：
X表示“不透明的袋子里有2红2白四个球，随机抓一个球，球的颜色”事件，
Y表示“不透明的袋子里有3红2白五个球，随机抓一个球，球的颜色”事件，
Z表示“不透明的袋子里有1红1白两个球，随机抓一个球，球的颜色”事件。
由于在事件X和Z中，都是P(红)=0.5 P(白)=0.5；而在事件Y中P(红)=0.6 P(白)=0.4，所以我们认为：相对于事件X，事件Y的差异程度大于事件Z，即：KL(Y||X) > KL(Z||X)。

那么该如何具体计算KL散度呢？
KL散度的数学定义为：
对于离散型随机变量，我们定义A和B的KL散度为：

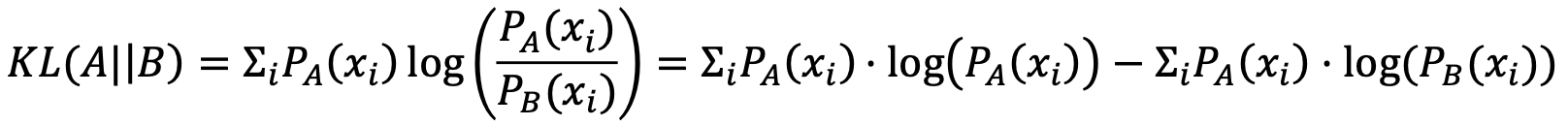
从编码的角度理解KL散度
在同样的字符集上，假设存在另一个概率分布Q(X)。如果用概率分布P(X)的最优编码（即字符x的编码长度等于log[1/P(x)]），来为符合分布Q(X)的字符编码，那么表示这些字符就会比理想情况多用一些比特数。KL-divergence就是用来衡量这种情况下平均每个字符多用的比特数，因此可以用来衡量两个分布的距离。

3. 交叉熵(Cross-Entropy)
   抽象解释：我所理解的交叉熵的含义，与KL散度是类似的，都是用于度量两个分布或者说两个随机变量、两个事件不同的程度。

具体例子：与KL散度类似

交叉熵的数学定义：

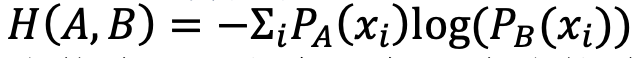
比较熵、KL散度和交叉熵的数学定义会发现：
KL散度 = 交叉熵 - 熵

从编码的角度理解交叉熵
熵的意义是：对一个随机变量A编码所需要的最小字节数，也就是使用哈夫曼编码根据A的概率分布对A进行编码所需要的字节数；
KL散度的意义是：使用随机变量B的最优编码方式对随机变量A编码所需要的额外字节数，具体来说就是使用哈夫曼编码却根据B的概率分布对A进行编码，所需要的编码数比A编码所需要的最小字节数多的数量；
交叉熵的意义是：使用随机变量B的最优编码方式对随机变量A编码所需要的字节数，具体来说就是使用哈夫曼编码却根据B的概率分布对A进行编码，所需要的编码数。

pytorch和tensorFlow的区别

pytorch 和 tensorflow1.0

首先我们要搞清楚pytorch和TensorFlow的一点区别，那就是pytorch是一个动态的框架，而TensorFlow（1.0）是一个静态的框架。何为静态的框架呢？我们知道，TensorFlow的尿性是，我们需要先构建一个TensorFlow的计算图，构建好了之后，这样一个计算图是不能够变的了，然后我们再传入不同的数据进去，进行计算。这就带来一个问题，就是固定了计算的流程，势必带来了不灵活性，如果我们要改变计算的逻辑，或者随着时间变化的计算逻辑，这样的动态计算TensorFlow是实现不了的，或者是很麻烦。

但是pytorch就是一个动态的框架，这就和python的逻辑是一样的，要对变量做任何操作都是灵活的。

举个简单的例子，当我们要实现一个这样的计算图时：

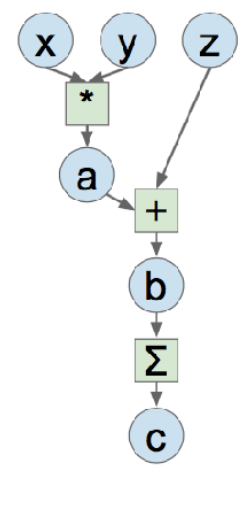
用TensorFlow是这样的：

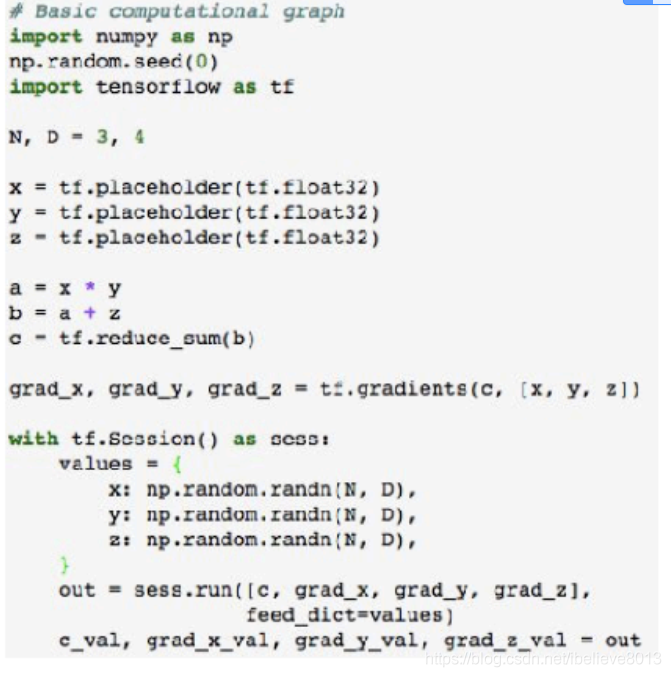
而用pytorch是这样的：

pytorch包括了三个层次：tensor,variable,Module。tensor，即张量的意思，由于是矩阵的运算，十分适合在GPU上跑。但是这样一个tensor为什么还不够呢？要搞出来一个variable，其实variable只是tensor的一个封装，这样一个封装，最重要的目的，就是能够保存住该variable在整个计算图中的位置，详细的说：能够知道计算图中各个变量之间的相互依赖关系。什么，你问这有什么用？当然是为了反向求梯度了；而Module，是一个更高的层次，如果使用这个Module，那可厉害了，这是一个神经网络的层次，可以直接调用全连接层，卷积层，等等神经网络。

Tensorflow1.0&Tensorflow2.0与pytorch框架的比较