向量运算实现碰撞系统_向量 计算 两个物体 是否碰撞

1.physx物理系统

我们在制作游戏时经常会用到碰撞检测，像当前主流的两大3D游戏引擎中的物理系统都是集成了physx物理系统。

Unity是通过collider确定形状，也是有physx所拥有的几个形状，椭圆碰撞体，圆碰撞体，正方碰撞体，网格碰撞体，地板碰撞体，三角面碰撞体，还有一些2d相关的碰撞体。然后用rigidbody来确定动态碰撞体，有了rigidbody就产生了trigger或者collider事件并且可以产生多个碰撞体之间的约束。

 

UE4中同样也是有physx所拥有的几个形状，椭圆碰撞体，圆碰撞体，正方碰撞体，网格碰撞体，地板碰撞体，三角面碰撞体。他通过FbodyInstance与physx连接来得到碰撞相关的效果。然后ue4中双击网格后找到启动模拟物理的tab里可以开启物理效果。

 

1. 分离轴技术(SAT)：

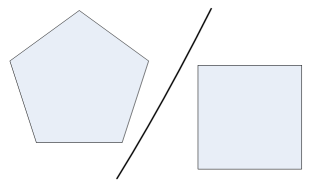
分离轴技术的是一项用于检测凸多边形碰撞的技术。它的原理来源于集合分析中的“分离超平面定理”（separating hyper-plane theorem）：如果两个集合A和B不相交，那么必定存在一个分离超平面P，并使得A和B分别位于P的不相同的两侧。

假设凸集A中含有FA个面、EA条边，凸集中含有FB个面、EB条边，这样就存在FA + FB + EA * EB条潜在的分离轴，某些情况下这个数量是巨大的，因而在实际情况中我们往往需要再根据具体几何体元的空间特征对其进行简化。比如，对于两个OBB之间的相交测试，由于OBB的六个面中两两相对的面是平行的，这样我们就可以将面－面之间的分离轴数目减少一半，同样也可以将边－边之间的分离轴数目减少一半，如此一来情况就简单了很多。

对于每条分离轴L，做投影计算得到d、RA、RB，并根据它们之间的关系得到分离关系。若d > RA +   RB则分离平面存在，即两个集合之间不相交，此时可以及时退出判断程序；反之，这两个集合在此分离轴下没有分离，但却也不能说明两个集合相交。

分离平面设置为：

1.      凸集A中每个多边形所在的平面。

2.      凸集B中每个多边形所在的平面。

3.      凸集A中的每条边和凸集B中的每条边之间的公共垂面。

分离轴方向为：

1.      凸集A中每个多边形的法向量。

2.      凸集B中每个多边形的法向量。

3.      凸集A中的每条边和凸集B中的每条边之间的公共垂面的法向量，即两条边方向向量的叉乘方向。

 

1. GJK算法：

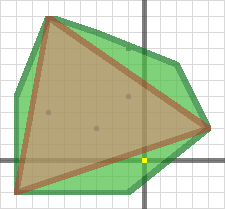
这个算法是基于一个叫明可夫斯基和/差的方式实现的。明可夫斯基和的做法是让物体1和物体2进行明可夫斯基减法操作，得到下面这个图，如果没有包括远点，则他们没有相交。这个得到的结论也比较好理解，如果一个面的点在另一个面里面，则他们有几个端点相减后的值会围绕圆形范围形成端点。

他的实现原理是如果两个物体(凸体)的明可夫斯基差形状中没有包括原点，则这两个物体不会相交(碰撞)。因此，我们不用采取迭代的方法不断计算包围原点的单纯形，而是想法得到一个离原点最近的单纯形。最近的单纯形总是在明可夫斯基差的边界上。对于2维的物体来说，最近的单纯形可能是一个点或者一条线，在三维的情况下，则可能是三角形或四面体。

 

连个物体之间的最短距离就是它们的明可夫斯基差形状到原点的最近距离。

 

和碰撞检测的GJK函数一样，计算距离的GJK函数也是迭代的。我们需要在明可夫斯基差形状中迭代地创建单纯形，使得单纯形包含到原点的最近点。求这个点的方法也要选择方向，使用support函数，以及检测终止条件等。

 

Support函数可以传递一个参数，该参数表示一个方向，方向不同，得到的点不同。这样的话我们就不会每次都得到相同的点了。

public Point support(Shape shape1, Shape shape2, Vector d)
 {
 
// d is a vector direction (doesn't have to be normalized)
 
// get points on the edge of the shapes in opposite directions
 
Point p1 = shape1.getFarthestPointInDirection(d);
 
 Point p2 = shape2.getFarthestPointInDirection(d.negative());
 
// perform the Minkowski Difference
 
Point p3 = p1.subtract(p2);
 
// p3 is now a point in Minkowski space on the edge of the Minkowski Difference
 
return p3;
 
}

不同方向得到的不同的面积。

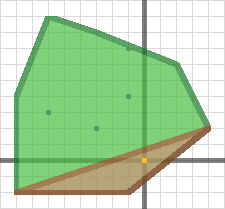
如果包含原点说明是相交的。

 

 

1. 向量计算方法：

我们也可以用向量的方式实现碰撞的检测，而在这里碰撞检测中比较典型的也是麻烦的就是胶囊体和长方体的碰撞检测了。而现在只做了计算方面，还没实现空间管理，空间管理其实可以用八叉树等实现，先减少向量计算方法的实现过程：

以下说明以下计算过程：

因为胶囊体实际上是一个中心线然后结合统一的半径组成的一个立体形状。

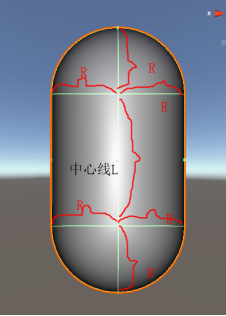
然后长方体是由六个面组成的立体图形。

而他们之间相交的条件就是他们的距离在一定范围以内。而像SAT和GJK都是要遍历所有的点或边才能得到最终是否相交的结论。而如果用向量实现所有面相交的可能性的话那么计算量就更大了。

 

4.1 计算与胶囊体最近的立方体的面

所以我们考虑减少他们的检测次数，尽量让他只检测一个面就能确定是否能碰撞。我用的方法是用长方体中心点到胶囊体的中心线最近的点的连线形成的向量与每个面的法线点乘，找点乘值最大的就认为他是离胶囊体最近的面，就只判断该面是否有相交就足够了。

这里有个要注意的是我们先要找到中心点到胶囊体最近的点：

这里首先还需要知道立方体中心点（boxCenter）到胶囊体中心线（capsuleCenterLine）的最短距离：

做法就是算出boxCenter与capsuleCenterLine的某一个端点的连线到capsuleCenterLine的投影，这个投影就是boxCenter在capsuleCenterLine的最近的点。距离就是相减后的值。

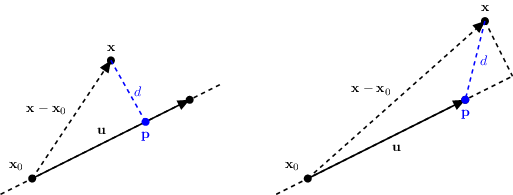
static float SegmentPointSqrDistance(Vector2 x0, Vector2 u, Vector2 x) {

    float t = Vector2.Dot(x - x0, u) / u.sqrMagnitude;

return (x - (x0 + Mathf.Clamp(t, 0, 1) * u)).sqrMagnitude;

}

 

 

4.2

确定了一个面之后我们就要开始判断当前的面是否与胶囊体相碰撞了。我们分析下胶囊体与面的相碰需要确定的条件，

第一个条件就是胶囊体中心线capsuleCenterLine的两个端点的投影是否在面内，如果在则端点与面的距离是否小于胶囊体的半径就可以确定是否相交了。

第二个条件就是如果胶囊体两个端点都不在面上则要判断胶囊体的中心线跟面的最短距离是否小于半径来确定是否相交。

 

4.2.1 点与面的距离

点和面的距离首先要看两个端点有没端点是不需要计算的，因为如果点不在面上就没必要计算他跟面的距离了，因为这个端点必然不会跟面相交。

首先要得到胶囊体端点到这个面的中心点的向量，以及四个点AB，BC的向量。如下图：

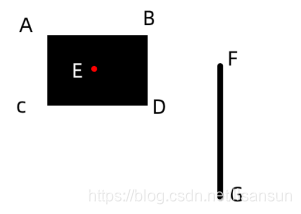
ABCD是一个面，FG是一条线，E是ABCD面的中心点。首先我们得到FE这个向量，然后跟ABCD的法线点乘，得到EF在面上的法线上的分量（向量在法线上的长度normalLength）。然后我们用faceLine=EF+normalLength*normal，根据向量相加得到了在面ABCD上的向量。然后用这个faceLine和两个向量AB和BC点乘得到faceLine在AB和BC上的分量。然后看他们的长度是否大于面ABCD上的宽高。如果都不大于说明这个点在面范围内，需要计算，如果不是则不计算。

当有点需要计算时，我们拿前面计算的EF在面上的法线上的分量是否小于胶囊体的半径，如果小于说明相交，就不需要再算了。

 

4.2.2 线和面的距离

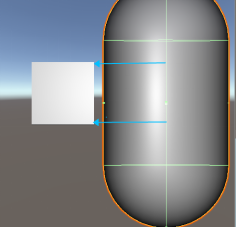
如果两个端点和面不相交，则我们要计算胶囊体整根线与面是否相交，而要计算线跟线的相交。因为这个情况下胶囊体的中心线可能比面大，所以必然跟面的四个边的某一边有最近点，所以我们可以判断胶囊体的中心线与面的四个边的最短距离，取最小的距离然后判断与半径的大小来判断是否相交。

首先我们需要知道线线最短距离的计算方式：

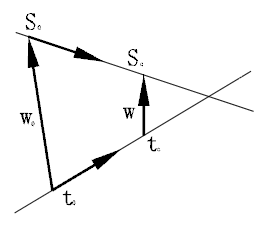
核心算法是，如果两条线段平行，那么距离是一个常数，也就是找点到线的距离即可。如果不平行，则找到一条线段Line，这条线段和两条线段（比如AB）和EF能连接在一起，同时这条线段Line也是唯一与两条直线同时垂直的线段。也就是AB点乘Line为0和EF点乘Line为0。然后解方程得到的公式。

具体可以参考：https://segmentfault.com/a/1190000006111226

 

然后找到EF与四个边的最短的距离后跟半径比较，小于半径就说明相交。

 

这里就是完整的算法了。然后我们要追求效率可以把vector3相关的改为float3这个库里面的方法，会快一点。然后我们可以把整个算法过程丢到jobsystem里面运算，并且用brust，效率可以得到进一步提升。下面是一些数据。

上面这个是14个box加一个capsule的数据，再没有jobsystem+brust下的消耗。

上面是14个box加一个capsule的数据，是带jobsystem+brust下的消耗。

 

这个是unity的物理碰撞跟我们向量实现的碰撞的一些比较数据。