LeetCode（力扣）初级算法 数组篇_leetcode 给定一个数组,每个元素的值是唯一的,找出其中两个原色相减等于给定差值

目录

1.删除排序数组中的重复项

1.1第一版代码

1.2第二版

1.3第三版

2.买卖股票的最佳时机 II

2.1第一版

2.2第二版

3.旋转数组

4.存在重复元素

5.只出现一次的数字

6.两个数组的交集 II

7.加一

7.1第一版代码

7.2第二版代码

8.移动零

9.两数之和

10.有效的数独

11.旋转图像

12.总结

---

1.删除排序数组中的重复项

题目要求：给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

 不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2gy9m/
来源：力扣（LeetCode）

分析思路：

        题目给出的数组是升序排序好的，意思也就是重复的元素会在数组中相邻的位置，所以我们是需要通过从左往右，比较相邻位置的元素看其是否相同，并且重复的元素并不止在数组中出现两次，会更多。最终结果需要保留k个不重复项。所以，我们有两种选择：一是记录每个元素的重复项个数，根据个数将其重复项删除，最终得到k个结果；二是在每种元素第一次出现时，直接将不重复的项数加1，将后续相同元素删除，直到得到k个结果。（重复个数：如1，1，3，3，3。1的重复个数为1，3的重复个数为2）

        我们需要比较在原位置的元素，与其后续相邻的多个元素。如果相邻位置的元素就不相同，那就不需要比较后续元素；如果相邻元素相同，就还需要一直往后， 进行比较，直到找到不同的元素。这里就需要比较两个位置的元素，一个在前，一个在后，这也就是双指针方法的应用。

        删除不一定是真的要把这个元素从数组中删除，我们可把找到的邻接的不同元素直接赋值给原位置元素的后一个位置，覆盖其重复项，达到删除重复项的目的。如果这个原位置元素没有重复项，那邻接的不同元素就在原位置元素的后一个位置，所以覆盖了也没关系。

1.1第一版代码

for (int i = 0; i < numsSize; i++) {//把后面全部的往前挪，太慢
	for (int j = i + 1; j < numsSize; j++) {
		if (nums[i] == nums[j]) {
			count++;//记录重复的个数
		}
		else break;
	}
	if (count > 0) {//将后面所有的元素往前挪
		for (int k = i,l = i + count; l<numsSize; k++,l++) {
		    nums[k] = nums[l];//把重复项的最后一位，接着后续所有元素往前挪
		}
		numsSize -= count;//元素总数将重复个数减去
		count = 0;//重置下一个元素的重复个数
	}
}
return numsSize ;//最终numsSize就是k

        第一版写的很粗糙，用了两个for循环，i为原位置元素，j指向其后续元素；使用了选择1：count记录了i的重复的个数。这里虽然用了两个for，但是还行。但是 if 那里就比较蠢了，把后续的所有元素都往前挪了count位。这就干了多余的操作了，时间复杂度本来可以是O(n)，现在直接飙到O(n^2)了。

1.2第二版

int count = 0; int left = 0; int right = 0;//双指针一个慢，一个快//不完善
for (; left < numsSize; left++) {
	right = left + 1;
	while(i < numsSize) {
		if (nums[left] != nums[right]) break;
		right++;//直到找到与原位置不同的元素，或达到边界停下
	}
	left = right - 1;//left是原位置元素重复项的最后一位，
                    //所以不用担心边界问题
	nums[count] = nums[left];//记录
	count++;
}
return count;

        这里虽然还是两个循环，但外循环会跳过内循环走过的地方，所以时间复杂度还是O(n)。这里没有使用单独变量记录元素重复个数，但在while中right-1与left的差值相当于元素的重复个数。left和right始终相邻。

        第二版还不够简洁。

1.3第三版

int left = 0;
for (int right = 1; right < numsSize; right++) {
    if(nums[left] != nums[right])
		 nums[++left] = nums[right];
}
return left + 1;

        这里直接使用left和right两个变量，left在原位置，right寻找其不同元素。找到时将right处元素放在left的下一个位置，然后循环再找现在left位置的元素的不同元素。相当于提前将数组第一个元素存在里面。所以left是不重复项最后一位的下标位置，所有最终left+1就是k。

2.买卖股票的最佳时机 II

题目要求：

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

思路分析：

        股票是时涨时跌的，并且在最低谷时买，在最顶峰时卖，是利润最大的。所以我想到：使用三个指针，前两个一起找最低点，后两个一起找两个最高点，找到后计算其获利。循环进行，直到达到边界。

2.1第一版

int maxProfit(int* prices, int pricesSize) {
	int count = 0, i = 0, all = 1; int f = 0;
	while (all < pricesSize) {
        //前低后高就是下坡，直到找到最低点或边界
		while (all < pricesSize&&prices[i] > prices[all]) {
			all++;
			i++;
		}
		f = all + 1;
        //前高后底就是上坡，直到找到最高点或边界
		while (f < pricesSize&&prices[f]>prices[all]) {
			f++; all++;
		}
		if (all < pricesSize) {
            //prices[all] >= prices[i]
			count += prices[all] - prices[i];
			i = all;
			all = f;
		}
		
	}
	return count;
}

2.2第二版

        在看了别人的思路后，我发现这其实就是要求最大利润，也就是记录所有上升区间的高度变化之和。 用后一天的股价减去前一天的股价，也就是前一天买入后一天卖出可得利润，将所有正数相加就是股价上涨的总和，也就是可获得的最大利润。

int maxProfit(int* prices, int pricesSize) {
	int count = 0;
    //最后一天只可能卖出，不会买进
	for (int i = 0; i < pricesSize - 1; i++) {
		prices[i] = prices[i + 1] - prices[i];
	}
	for (int i = 0; i < pricesSize - 1; i++) {
		if (prices[i] > 0) count += prices[i];
	}
	return count;
}

3.旋转数组

题目要求：

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

思路分析：

        旋转数组，向右轮转k个位置，也就是将数组中后k个元素移动到数组最左端，其他元素全部向右移k位。

        在没有特殊要求，或者我们没有很好的方法前，我们可能会想到用一个O(n)大小的数组空间来辅助。也或者是真用O(1)大小的空间辅助，将数组元素一个一个移动。（在不会下面说的方法前，我的确可能这样做）（但是我知道，就没那样写，嘿）

        将整个数组逆序不也是一种将后方元素转移到数组前方的方法吗，只要我们再在k位置处为界限，将k之前和包括k到之后的两块区域分别再逆序，将两个区域中的元素分别转换成其原来顺序，就完成了旋转数组。

        所以我们先编写一个将数组按照我们规定位置进行逆序交换的函数。

void Exchange(int* nums, int start, int end) {
	end--;
	if (start >= end) return;
	int tmp = 0;
	while (start < end) {//数组前后位置元素互换位置
		tmp = nums[start];
		nums[start] = nums[end];
		nums[end] = tmp;
		start++; end--;
	}
}

        再根据我们需要调用三次就行了。//如果k大于数组长度，则旋转后的效果与旋转k对numsSize取余的结果次一样。

void rotate(int* nums, int numsSize, int k) {
    if (k > numsSize) k = k % numsSize;
	Exchange(nums, 0, numsSize );
	Exchange(nums, k, numsSize );
	Exchange(nums, 0, k);
}

4.存在重复元素

题目要求：

给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ，返回 true ；如果数组中每个元素互不相同，返回 false 。

提示：

• 1 <= nums.length <= 10^5
• -109 <= nums[i] <= 109

思路分析：

        题目没说数组是有序的，所以我们不能直接上手对相邻元素进行比较。所以我们可以先排序，再进行相邻数据比较。

int cmp(const void*a,const void*b){
    return *(int*)a-*(int*)b;//递增
}
 
bool containsDuplicate(int* nums, int numsSize){
    qsort(nums,numsSize,sizeof(int),cmp);
    for(int i=0;i<numsSize-1;i++){
        if(nums[i]==nums[i+1]){
            return 1;
        }
    }
    return 0;
}

        这里使用了系统提供的排序函数qsort()，nums是要排序的数组，numsSize是要排序的数组长度，sizeof（int）是数组元素大小，cmp是一个比较元素大小的回调函数。上述代码中cmp函数使得qsort函数牌序数组以升序排序。若要降序排序，将return中a和b调换位置。

        也可以使用哈希表，但我不太会，数据范围太大了。

5.只出现一次的数字

题目要求：
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x21ib6/
来源：力扣（LeetCode）

思路分析：

        在本题中，数组也没有说是有序的。与题4有点相似：我们也可以在排序后，通过比较相邻数组元素，判断该元素是否是单独的。快排的时间复杂度为O(nlogn)，除了基数排序，没有时间复杂度更低的排序方法了，但是我不了解基数排序，所以算法不是线性的，并且排序时需要额外空间。但是在没有好方法时，就只会这样做。

        可惜，我学到了一个满足题目要求的方法：以0对数组中所有元素进行异或，结果就是那个单独的数。因为0异或任何数都等于这个数，任何数异或其本身都等于0，并且异或运算是可交换的（即数组元素顺序不影响结果），所以相当于出现两次的数都自己异或自己变成了0，最后0异或这个出现一次的数等于这个只出现一次的数。

int singleNumber(int* nums, int numsSize){
    int flag=0;
    for(int i=0;i<numsSize;i++){
        flag=flag^nums[i];
    }
    return flag;
}

6.两个数组的交集 II

题目要求：
给你两个整数数组 nums1 和 nums2 ，请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数，应与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。可以不考虑输出结果的顺序。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2y0c2/
来源：力扣（LeetCode）

思路分析：

        首先，数组是无序的，还要比较其各元素的出现次数才能解决。所以，可以使用哈希表将nums1中的每个元素按顺序存入哈希表，并记录数量，碰到相同元素时该元素的数量+1。将nums2中的元素与哈希表中的元素进行比较，如果存在，则哈希表中该元素的数量减一，将该元素存入另外新建的交集空间中，如果哈希表中该元素数量变为0，则将该元素从哈希表删除。But，我不太会，在我的理解下，我会开辟额外很大的空间，然后程序的时间复杂度在O(n^2)（主要在往哈希表存数据时）。（所以哈希表还是很重要的，可以用来解很多题）

        所以，我还是采用另一种方法：先对两个数组（num1，num2）分别进行排序，然后从两数组头部开始，比较两数组的元素大小（num1[i],num2[j]），如果num1[i] < num2[j]，i++，直到num1[i]==num2[j]，或num1[i] > num2[j]。如果num1[i]==num2[j]，记录num1[i]，i++，j++；如果num1[i] > num2[j]，就对num2[j]进行刚才num1[i]的操作，直到走完一个数组。

        所记录下来的元素就是交集的所有元素。

void swap(int* arr, int i, int j) {
	int tmp = arr[i];
	arr[i] = arr[j];
	arr[j] = tmp;
}
 
void bsort(int* arr, int len) {//实现了冒泡排序
	for (int i = 0; i < len - 1; i++) {
		for (int j = i + 1; j < len; j++) {
			if (arr[i] > arr[j]) {
				swap(arr, i, j);
			}
		}
	}
}
int* intersect(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    //交集长度肯定<=两数组最短长度
	int len = nums1Size < nums2Size ? nums1Size : nums2Size;
    //动态内存开交集空间
	int* p = (int*)calloc(len, len*sizeof(int));
	*returnSize = 0;
	if (p == NULL) return p;
 
    bsort(nums1, nums1Size);
	bsort(nums2, nums2Size);
 
	int l = 0;//记录交集元素个数
	//int i = 0, j = 0;
	for (int i = 0, j = 0; i < nums1Size && j < nums2Size;) {
		while (i< nums1Size && nums1[i] < nums2[j]) i++;
		if (i >= nums1Size) break;
		while(j < nums2Size && nums1[i] > nums2[j]) j++;
		if (j >= nums2Size) break;
		while (nums1[i] == nums2[j]&& i < nums1Size && j < nums2Size&&l < len) {
			p[l] = nums1[i];
			i++; j++; l++;
		}
	}
	*returnSize = l;
	return p;
}

7.加一

题目要求：
给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2cv1c/
来源：力扣（LeetCode）

思路分析：

        这是一个数组，数组元素是单独的个位数，用来模拟十进制数组。分两种情况：一种是数组元素全为9时，加一后十进制数字会进位，所以数组需要扩容一位来接收进位的1；第二种情况就是数组元素不全为9，虽然里面会发生进位，但数组不需要扩容。

        因为可能会要进行扩容，所以我们直接使用动态内存开辟出一段比数组长1的内存。并且进位时，是向左边进位的，所以我想到将数组进行逆序，再运算。

7.1第一版代码

int* plusOne(int* digits, int digitsSize, int* returnSize) {
    //开辟比数组长一位的空间
    int* arr = (int*)calloc((digitsSize + 1),sizeof(int) * (digitsSize + 1));
    if (arr == NULL)return 0;
    int i = 0, j = digitsSize - 1;
    //将数组逆序
    while (i < digitsSize) {
        arr[j--] = digits[i++];
    }
    arr[0]++; //原数组数字最低位加一
    j++;//j从-1到0
    int count = 0;//记录进位次数
    //看是否发生进位
    while (arr[j] > 9) {
        arr[j] = arr[j] % 10;
        j++;
        arr[j]++;
        count++;
    }
    //如果进位次数等于数组长度，
    //意味着原数组所有元素都是9，全部进位，数组长度+1；记录返回长度
    i = 0; j = count == digitsSize ? digitsSize : digitsSize - 1;
    *returnSize = j + 1;//j+1
    int tmp = 0;
    //再将数组逆序
    while (i < j) {
        tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
        i++; j--;
    }
    return arr;
}

7.2第二版代码

        虽然但是，代码实现的不好，看最上面分析的，只有在所有元素都是9的这个极端条件下才需要数组扩容。所以上面那个就是*，进行优化：

int* plusOne(int* digits, int digitsSize, int* returnSize) {
    int i = digitsSize-1;
    *returnSize=digitsSize;//数组长度先赋为原长
    //倒着比较数组元素是否大于9
    while (i >=0 ) {
        if (digits[i] != 9) {
            digits[i]++;//不是9就直接+1，退出
            return digits;
        }
        else {
            digits[i] = 0;//是9就变0，进位1
        }
        i--;
    }
    //没在循环中退出，就意味着所以元素都是9，所以数组扩容
    int* arr = (int*)calloc((digitsSize + 1), sizeof(int) * (digitsSize + 1));
    if (arr == NULL)return 0;
    *returnSize=digitsSize+1;//长度+1
    //数字最高位为1
    arr[0] = 1;
    //其余均为0
    for (i = 1; i < digitsSize + 1; i++) {
        arr[i] = 0;
    }
    return arr;
}

8.移动零

题目要求： 

 给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2ba4i/
来源：力扣（LeetCode）

思路分析：

        这一题与第一题删除数组重复项一样。所以我的思路和第一题很相似。在明白了第一题的最优思路后，代码就呼之欲出了。

        将不为0的数字按顺序从0号下标开始向后存放，直接覆盖原值（双指针方法），记录末尾下标。然后将下标位置之后的所有元素赋值为0，即完成了0的移动。

void moveZeroes(int* nums, int numsSize) {
	int index = 0;
	for (int i = 0; i < numsSize; i++) {
		if (nums[i] != 0) {
			nums[index++] = nums[i];
		}
	}
	while (index < numsSize) {
		nums[index++] = 0;
	}
}

9.两数之和

题目分析：
给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

提示：

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2jrse/
来源：力扣（LeetCode）

思路分析：

        很简单，双重for循环，先找一个x，再在数组里找target-x。进阶方法就是哈希表。

int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
	static int arr[2] = { 0 }; int flag = 0;
	*returnSize = 0;
	for (int i = 0; i < numsSize; i++) {
		for (int j = i + 1; j < numsSize; j++) {
			if (nums[j] == target - nums[i]) {
				arr[0] = i;
				arr[1] = j;
				flag = 1;
				*returnSize = 2;
				break;
			}
		}
		if (flag == 1) break;
	}
	return arr;
}

10.有效的数独

题目要求：
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
 

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/x2f9gg/
来源：力扣（LeetCode）

        这个不太会，就硬判断，先是9个九宫格，后是行和列。

bool isValidSudoku(char** board, int boardSize, int* boardColSize) {
 
	for (int i = 0; i < boardSize;) {
		for (int j = 0; j < *boardColSize;) {
			for (int k = i; k < i + 3; k++) {
				for (int l = j; l < j + 3; l++) {
					if (board[k][l] == '.') continue;
					for (int m = i; m < i + 3; m++) {
						for (int n = j; n < j + 3; n++) {
							if (m == k && n == l) continue;
							if (board[m][n] == '.') continue;
							if ((board[m][n] < '0' || board[m][n]>'9') && board[m][n] != '.') return 0;
							if (board[k][l] == board[m][n]) return 0;
						}
					}
				}
			}
			j = j + 3;
		}
		i = i + 3;
	}
   for (int i = 0; i < boardSize;i++) {
		for (int j = 0; j < *boardColSize;j++) {
			if (board[i][j]=='0') continue;
			for (int k = j + 1; k < *boardColSize; k++) {
				if (board[i][k]=='.') continue;
				if (board[i][j]== board[i][k]) return 0;
			}
		}
		for (int j = 0; j < *boardColSize; j++) {
			if (board[j][i]=='.') continue;
			for (int k = j + 1; k < boardSize; k++) {
				if (k == j) continue;
				if (board[k][i]=='.') continue;
				if (board[j][i]== board[k][i]) return 0;
			}
		}
	}
	return 1;
}

11.旋转图像

题目要求：
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

作者：力扣 (LeetCode)
链接：https://leetcode.cn/leetbook/read/top-interview-questions-easy/xnhhkv/
来源：力扣（LeetCode）

思路分析：

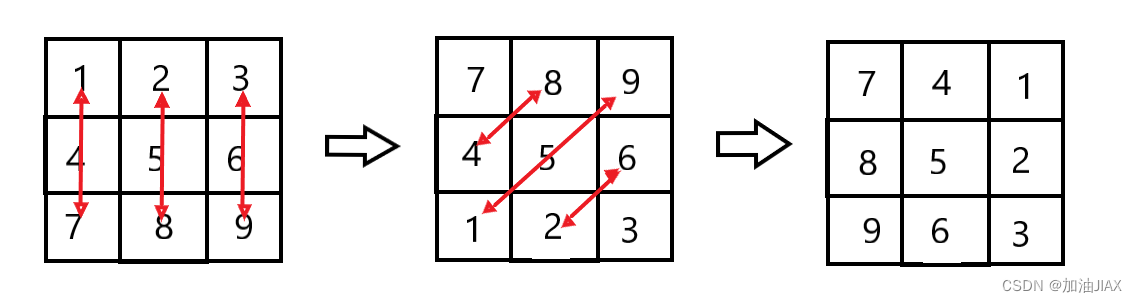
        在不知道或忘记数学的方法时，我只会用另外一个矩阵来实现。所以在学习了其他高手的题解之后，明白了旋转n*n矩阵可通过：先将上下部分进行对称交换，在以对角线进行对称交换实现。

void rotate(int** matrix, int matrixSize, int* matrixColSize) {
	if (matrixSize <= 1) return;
 
	for (int i = 0; i < matrixSize / 2; i++) {
		int *p = matrix[i];
		matrix[i] = matrix[matrixSize - 1 - i];
		matrix[matrixSize - 1 - i] = p;
	}
	for (int i = 0; i < matrixSize;i++) {
		for (int j = 0; j < i; j++) {
			int tmp = matrix[i][j];
			matrix[i][j] = matrix[j][i];
			matrix[j][i] = tmp;
		}
	}
}

        题中，函数二维数组传参采用二级指针，所以可以直接在第一个for循环中交换整个一维数组。

12.总结

        1.双指针法是一个很好用的方法，用来比较数组中的元素。

        2.要注意边界问题，将边界判断放在值判断左边，因为&&、||是从左向右执行的。

        3.哈希表是个好东西，要早点学会。

        4.分析好题目，并依次进行代码实现，避免做无用功。

        5.先自主思考问题，使用自己能想到的办法对题目进行解答。再学习别人优秀的题解，进行优化。

        6.多学习他人优秀题解。