【python机器学习】K-Means算法详解及给坐标点聚类实战（附源码和数据集 超详细）_kemeans python和数据

需要源码和数据集请点赞关注收藏后评论区留言私信~~~

人们在面对大量未知事物时，往往会采取分而治之的策略，即先将事物按照相似性分成多个组，然后按组对事物进行处理。机器学习里的聚类就是用来完成对事物进行分组的任务

一、样本处理

聚类算法是对样本集按相似性进行分簇，因此，聚类算法能够运行的前提是要有样本集以及能对样本之间的相似性进行比较的方法。

样本的相似性差异也称为样本距离，相似性比较称为距离度量。

设样本特征维数为n，第i个样本表示为x_i={x_i^(1),x_i^(2),…,x_i^(n)}。因此，样本也可以看成n维空间中的点。当n=2时，样本可以看成是二维平面上的点。

二维平面上两点x_i和x_j之间的欧氏距离： 

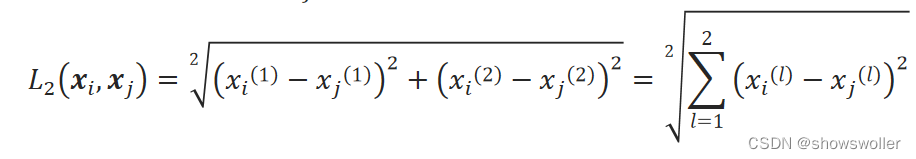
K均值聚类算法常采用欧氏距离作为样本距离度量准则。

二维平面上两点间欧氏距离的计算公式推广到n维空间中两点x_i和x_j的欧氏距离计算公式：

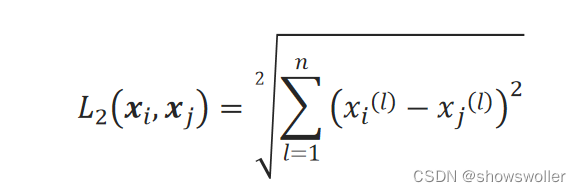
二、基本思想

设样本总数为m，样本集为S={x_1,x_2,…,x_m}。K均值聚类算法对样本集分簇的个数是事先指定的，即k。设分簇后的集合表示为C={C_1,C_2,…,C_k}，其中每个簇都是样本的集合。

K均值聚类算法的基本思想是让簇内的样本点更“紧密”一些，也就是说，让每个样本点到本簇中心的距离更近一些。

常采用该距离的平方之和作为“紧密”程度的度量标准，因此，使每个样本点到本簇中心的距离的平方和尽量小是k-means算法的优化目标。每个样本点到本簇中心的距离的平方和也称为误差平方和（Sum of Squared Error, SSE）。

从机器学习算法的实施过程来说，这类优化目标一般统称为损失函数（loss function）或代价函数（cost function）。

三、簇中心的计算

当采用欧氏距离，并以误差平方和SSE作为损失函数时，一个簇的簇中心按如下方法计算：

对于第i个簇C_i，簇中心u_i=(u_i^(1),u_i^(2),…,u_i^(n))为簇C_i内所有点的均值，簇中心u_i第j个特征为

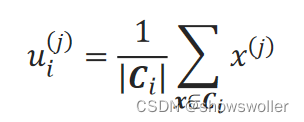
 SSE的计算方法为：

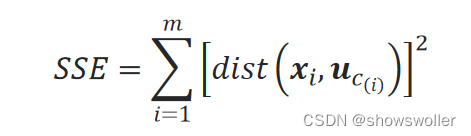
四、算法流程

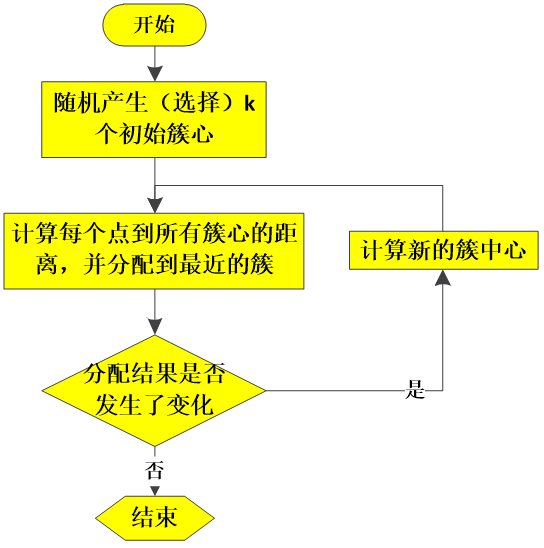
 五、对坐标点聚类实战

坐标点存在txt文件中 需要源码和数据集请点赞关注收藏后评论区留言私信~~~

K均值聚类算法以计算簇中心并重新分簇为一个周期进行迭代，直到簇稳定，分配结果不再变化为止，下面来看一个对二维平面上的点进行聚类的例子

效果展示如下

经过不断的迭代SSE误差在不断的减小，图像中的聚类也变得更为清晰，直到最后一个图变为三个较为稳定的簇

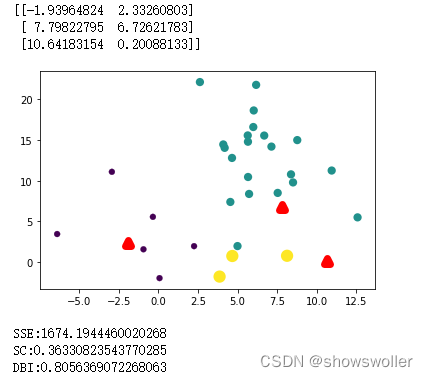
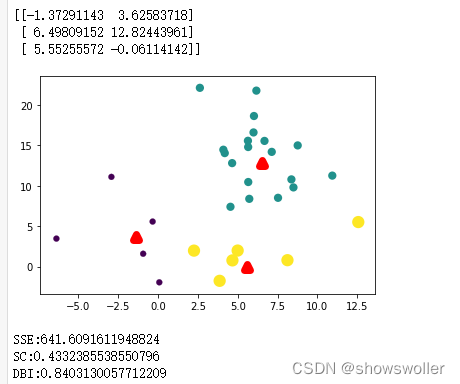
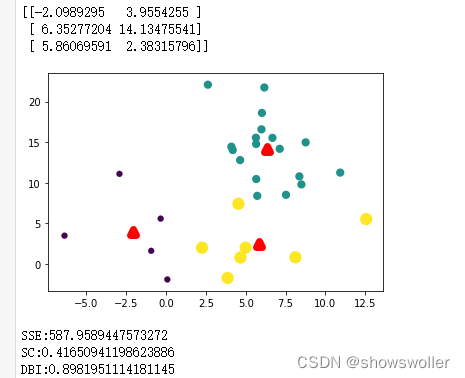
 部分代码如下

def L2(vecXi, vecXj):
    return np.sqrt(np.sum(np.power(vecXi - vecXj, 2)))
 
from sklearn.metrics import silhouette_score, davies_bouldin_score
def kMeans(S, k, distMeas=L2):
    m = np.shape(S)[0] # 样本总数
    sampleTag = np.zeros(m)
    n = np.shape(S)[1] # 样本向量的特征数
    clusterCents = np.mat([[-1.93964824,2.33260803],[7.79822795,6.72621783],[10.64183154,0.20088133]])
    #clusterCents = np.mat(np.zeros((k,n)))
    #for j in range(n):
    #    minJ = min(S[:,j]) 
    #    rangeJ = float(max(S[:,j]) - minJ)
    #    clusterCents[:,j] = np.mat(minJ + rangeJ * np.random.rand(k,1))
 
plt.scatter(clusterCents[:,0].tolist(),clusterCents[:,1].tolist(),c='r',marker='^',linewidths=7)
        plt.scatter(S[:,0],S[:,1],c=sampleTag,linewidths=np.power(sampleTag+0.5, 2)) # 用不同大小的点来表示不同簇的点
        plt.show()
        print("SSE:"+str(SSE))
        print("SC:"+str(silhouette_score(S, sampleTag, metric='euclidean')))
        print("DBI:"+str(davies_bouldin_score(S, sampleTag)))
 
        print("- - - - - - - - - - - - - - - - - - - - - - - -")
        
        # 重新计算簇中心
        for i in range(k):
            ClustI = S[np.nonzero(sampleTag[:]==i)[0]]
            clusterCents[i,:] = np.mean(ClustI, axis=0) 
    return clusterCents, sampleTag, SSE
 

创作不易 觉得有帮助请点赞关注收藏~~~