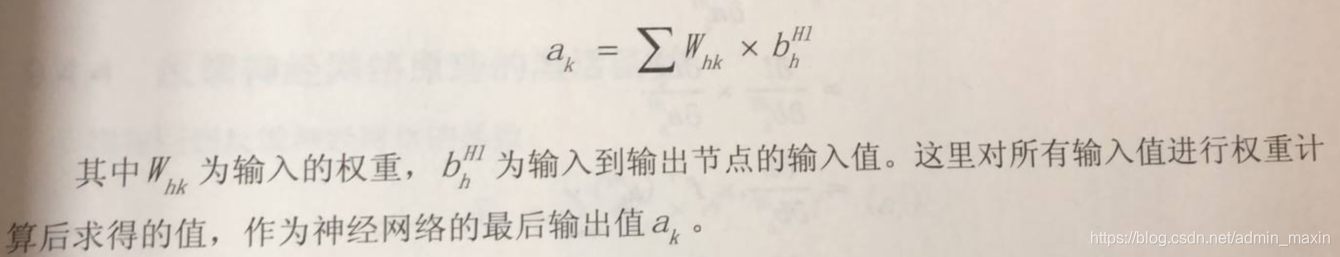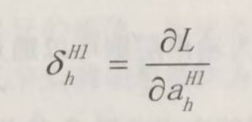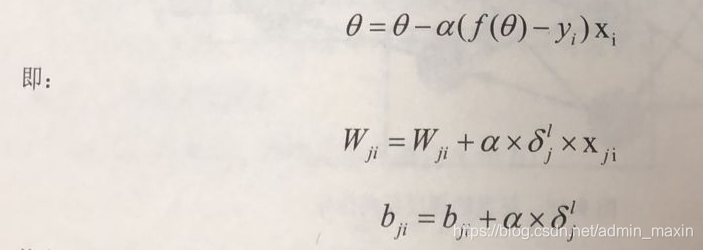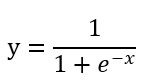机器学习 | 神经网络 —— BP神经网络（反馈神经网络：方向传播算法）_bp反馈

目录

1.反馈神经网络原理及公式推导

2.反馈神经网络原理与公式推导

2.1 原理

2.2 公式推导

2.2.1 定义一：前项传播算法

2.2.2 定义二：反向传播算法

 2.2.3 定义三：权重的更新

2.2.4 激活函数

3.反馈神经网络python实现（BP）

---

1.反馈神经网络原理及公式推导

梯度下降算法在衡量模型的优劣的过程中，需要计算梯度，即求不同权重的偏导数。因此，当隐层神经元个数增加（权重个数增加）或隐层个数增加（求导过程拉长）会大大拉长计算过程，即很多偏导数的求导过程会反复涉及到，因此在实际中对于权值达到上十万和上百万的神经网络来说，此种重复冗余的计算会浪费大量的计算资源。

同样是为了求得对权重的更新，反馈神经网络算法将误差E作为以权重向量中每个元素为变量的高纬函数，通过不断的更新权重，寻找训练误差的最低点，按误差函数梯度下降的方向更新权值。

2.反馈神经网络原理与公式推导

2.1 原理

误差反向更新

step 1.计算输出层与真实层之间差值

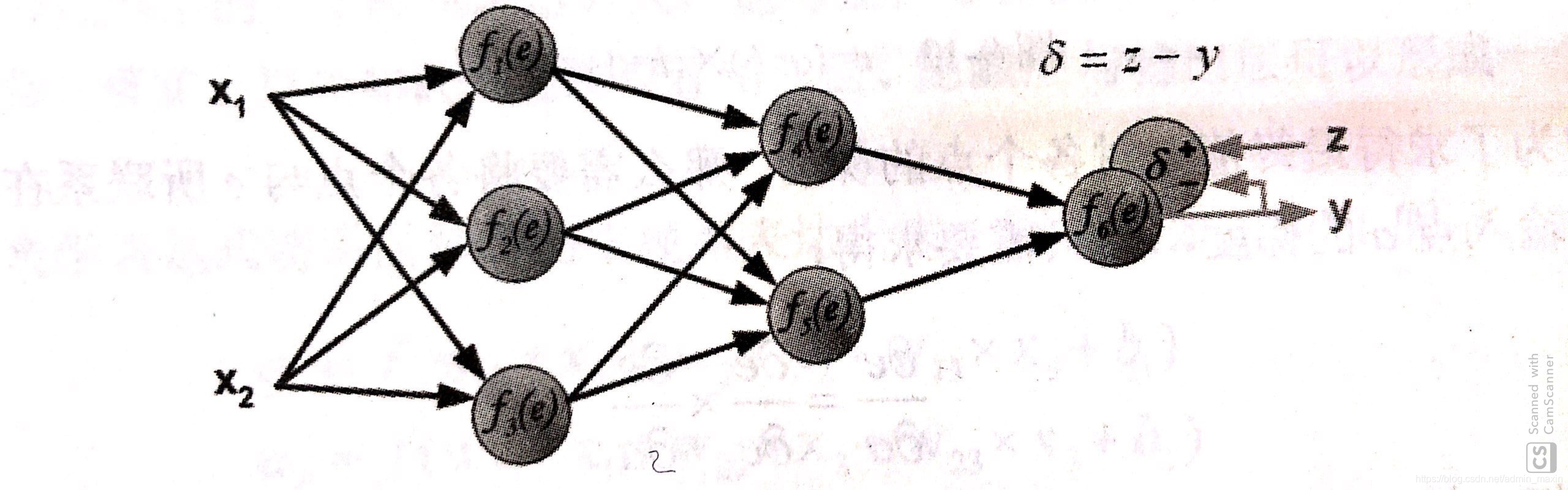
step 2.反向传播到上一个节点，计算出节点误差值

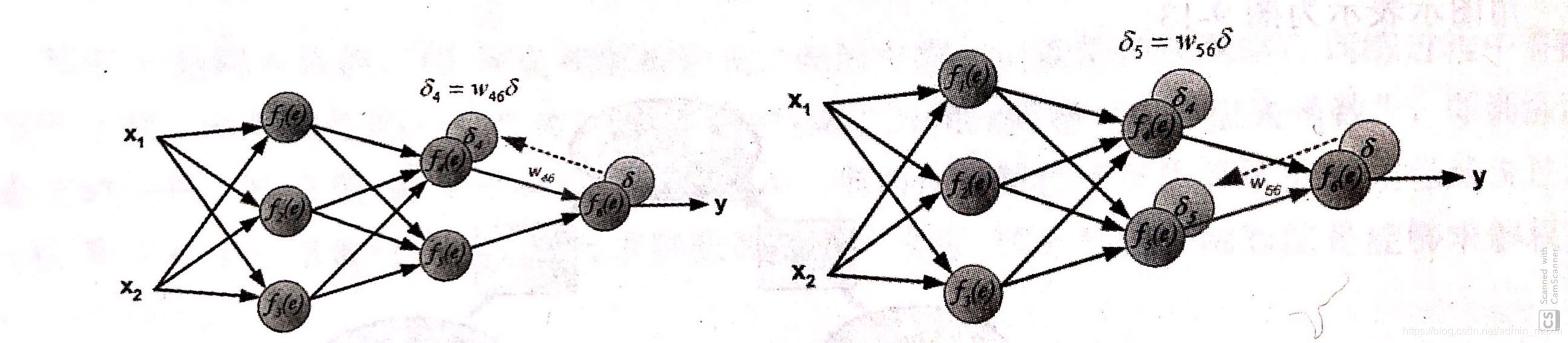
step3. 以step2中计算出的误差为起点，依次向后传播误差。（隐藏层误差由多个节点共同确定：加权和）

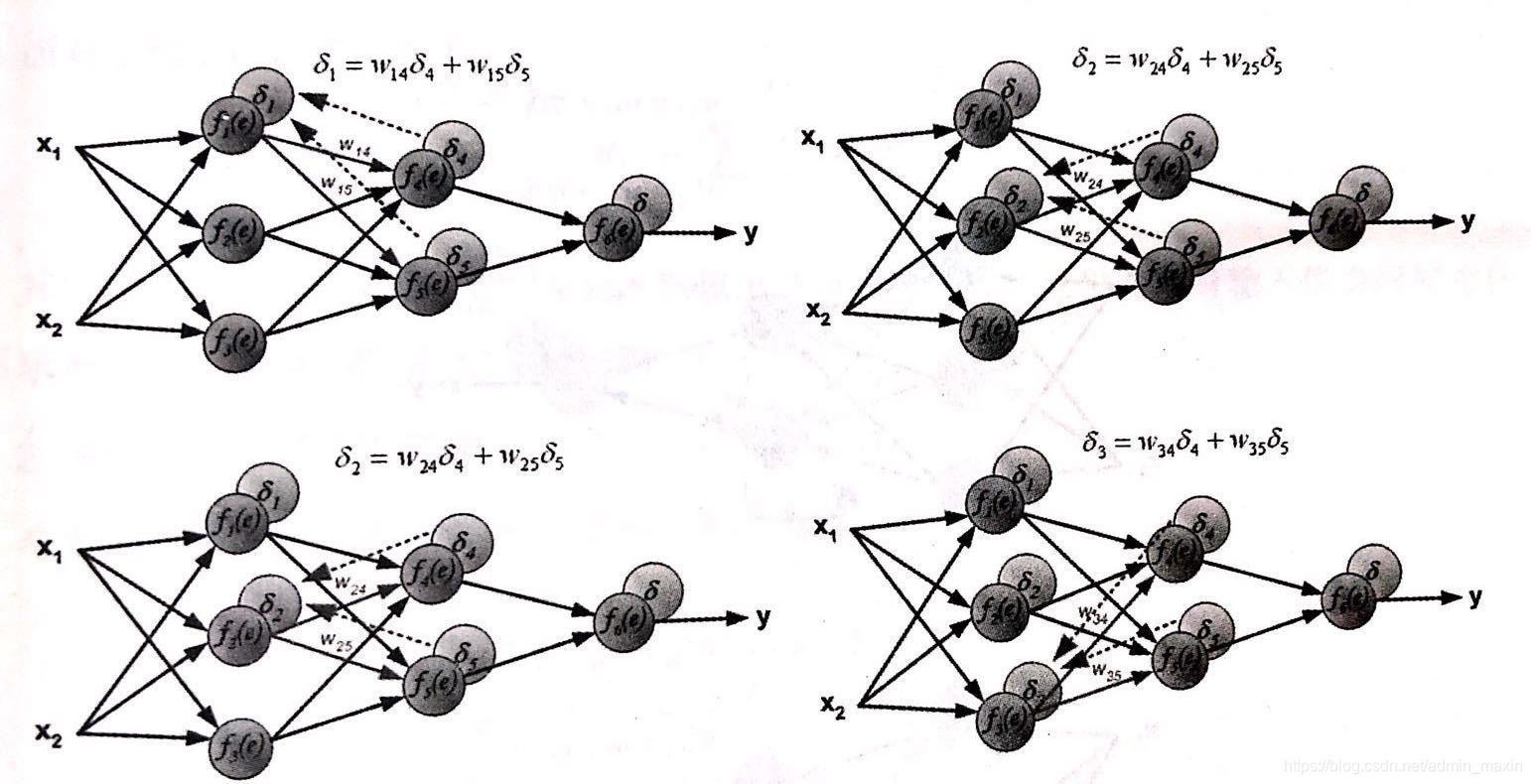
权值正向更新

step4. 通俗解释，误差的产生是由于输入值和权重的计算产生的，同时，输入值往往固定，因此，对于误差的调节只能通过权重的更新。权重的误差是以预测值与真实值之间的误差为基础的，当step1中所计算出的误差被一层层反向传播回来后，每个节点则仅需要更新其所需承担的误差量。

 为权重更新之前的权重值，学习速率，当前层当前神经元所对应的误差，当前层中当前神经元的输入（也是前一层的输出）。注：权重更新过程中是减法

2.2 公式推导

【注意事项】

①对于输出层单元，误差项是真实值与模型计算值之间的差值

②对于隐藏层单元，因为缺少直接的目标值来计算隐藏单元的误差因此需要以间接的方式来计算隐藏层的误差项对受隐藏层影响的每一个单元的误差进行加权求和。

③权值的更新方向，主要依靠学习速率、该权值对应的输入，以及单元的误差项。

2.2.1 定义一：前项传播算法

隐藏层的输出值：

 输出层的输出值：

2.2.2 定义二：反向传播算法

L：激活函数

输出层的误差项：

 输出层的误差：

【提示】

对于“输出层的误差项”和“输出层的误差”来说，无论定义在哪个位置，都可以看做当前的输出值对于输入值的梯度计算。（当前层的输出值对输入值的偏导数）

反馈神经网络计算公式：

为当前层的下一层的权值和误差的乘积的和，为当前层的输出值对输入值的梯度，即将当前层的输出值带入梯度函数的导函数中。

或者换一种表述形式将上图中的最终公式转换为：

 2.2.3 定义三：权重的更新

反馈神经网络计算的目的是对权重的更新，因此与梯度下降算法类似，其更新可以仿照梯度下降对权值的更新公式：

 其中，ji表示为反向传播是对应的节点系数，通过计算当前层输出对于输入的梯度，就可以更新对应的权重。b的更新类似。

2.2.4 激活函数

对于生物神经元来说，传递进来的电信号通过神经元进行传递，由于每个神经元的突出强弱是有一定的敏感度的，也就是只会对超过一定范围的信号进行反馈。即这个电信号必须大于某个阙值，神经元才会被激活引起后续的传递。以前应用范围较广的为Sigmod函数。因为，其在运行过程中只接受一个值输出，也为一个值的信号，且其输出值为0到1之间。

 图像为：

 导数：

说明：

Sigmod函数讲一个实数值压缩到0~1之间，特别是对于较大的值的负数被映射成为0，而较大的正数被映射成为1，所以，其经常容易出现区域饱和，即：当一开始数值非常大或非常小时，该区域的梯度（偏导数值：斜率）均接近于0，这样在后续的传播时会造成梯度消散的现象，因此，并不适合现代的神经网络模型的使用。

近年来大量的激活函数模型，均为解决传统的sigmod模型在更新程度上的神经网络所产生的各种不良影响。Maxout、Tanh和ReLU

3.反馈神经网络python实现（BP）

import numpy as np
import math
 
 
# ==1.定义辅助函数
def make_matrix(m, n):
    """
    生成(m, n)列的矩阵
    :param m: 行
    :param n: 列
    :return: 返回m行n列数组
    """
    return np.zeros((m, n))
 
 
def sigmoid(x):
    """
    激活函数
    :param x: 转换数值
    :return: 返回0~1之间的小数
    """
    return 1.0 / (1.0 + math.exp(-x))
 
 
def sigmoid_derivate(x):
    """
    激活函数的导数
    :param x: 转换数值
    :return: 导数值
    """
    return x*(1 - x)
 
 
class BPNeuralNetwork:
    """
    BP神经网络类
    """
    def __init__(self):
        """
        数据内容初始化
        """
        # 输入层数
        self.input_n = 0
        # 隐藏层数
        self.hidden_n = 0
        # 输出层数
        self.output_n = 0
        # 输入层输入数据
        self.input_cells = []
        # 隐藏层输出数据
        self.hidden_cells = []
        # 输出层输出数据
        self.output_cells = []
        # 输入层权重数据
        self.input_weights = []
        # 输出层权重数据
        self.output_weights = []
 
    def setup(self, ni, nh, no):
        """
        对init中定义的数据进行初始化
        :param ni: 输入层节点个数 2
        :param nh: 隐藏层节点个数 5
        :param no: 输出层节点个数 1
        :return: None
        """
        # 第一列为偏执项（调整分类决策面）
        self.input_n = ni + 1
        self.hidden_n = nh
        self.output_n = no
 
        # 初始化节点数值
        self.input_cells = [1.0] * self.input_n
        self.hidden_cells = [1.0] * self.hidden_n
        self.output_cells = [1.0] * self.output_n
 
        # 定义输出层和隐藏层权重矩阵
        # x:(3000, 2)
        # iw:(2(特征数), 4(隐层神经元个数))
        # o:(3000, 4)
        # ow:(4, 1)
        # re:(3000, 1)
        self.input_weights = make_matrix(self.input_n, self.hidden_n)
        self.output_weights = make_matrix(self.hidden_n, self.output_n)
 
        # 随机填充权重矩阵元素值
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                self.input_weights[i][h] = np.random.uniform(-0.2, 0.2)
        for h in range(self.hidden_n):
            for o in range(self.output_n):
               self.output_weights[h][o] = np.random.uniform(-0.2, 0.2)
 
    def predict(self, inputs):
        """
        反馈神经网络前向计算
        :param inputs: 输入层数据(一行：一个对象)
        :return: 输出层数据
        """
        # 将对象数据传入input_cells
        for i in range(self.input_n - 1):
            self.input_cells[i] = inputs[i]
 
        # 计算隐藏层输出
        for j in range(self.hidden_n):
            total = 0.0
            for i in range(self.input_n):
                total += self.input_cells[i] * self.input_weights[i][j]
            self.hidden_cells[j] = sigmoid(total)
 
        # 计算输出层输出
        # self.hidden_cells.shape = (1, 4)
        for k in range(self.output_n):
            total = 0.0
            for j in range(self.hidden_n):
                total += self.hidden_cells[j] * self.output_weights[j][k]
            self.output_cells[k] = sigmoid(total)
        return self.output_cells[:]
 
    def back_propagate(self, case, label, learn):
        """
        误差反向传播,并更新权重和偏执项
        :param case: 输入层数据(一个对象)
        :param label: 当前对象对应的分类标签
        :param learn: 学习速率
        :return: 当前对象的预测误差
        """
        # 先正向传播
        self.predict(case)
 
        # 计算输出层误差
        # error:误差项
        # output_deltas:误差
        output_deltas = [0.0] * self.output_n
        for k in range(self.output_n):
            error = label[k] - self.output_cells[k]
            output_deltas[k] = sigmoid_derivate(self.output_cells[k]) * error
 
        # 计算隐藏层误差
        hidden_deltas = [0.0] * self.hidden_n
        for j in range(self.hidden_n):
            error = 0.0
            for k in range(self.output_n):
                error += output_deltas[k] * self.output_weights[j][k]
            hidden_deltas[j] = sigmoid_derivate(self.hidden_cells[j]) * error
 
        # 更新隐藏层权重
        for i in range(self.input_n):
            for j in range(self.hidden_n):
                self.input_weights[i][j] += learn * hidden_deltas[j] * self.input_cells[i]
 
        # 更新输出层权重
        for j in range(self.hidden_n):
            for k in range(self.output_n):
                self.output_weights[j][k] += learn * output_deltas[k] * self.hidden_cells[j]
 
        error = 0
        for o in range(len(label)):
            error += 0.5 * (label[o] - self.output_cells[o])**2
 
        return error
 
    def train(self, cases, labels, maxiter=100, learn=0.05):
        """
        模型训练函数
        :param cases: 数据集
        :param labels: 标签集
        :param limit: 最大迭代次数
        :param learn: 学习速率
        :return: None
        """
        # 迭代maxiter次
        total_error = []
        for i in range(maxiter):
            # 遍历每一个对象
            error = 0
            for i in range(len(cases)):
                label = labels[i]
                case = cases[i]
                error += self.back_propagate(case, label, learn)
            total_error.append(error)
        return total_error
 
    def test(self):
        """
        模型预测函数
        :return: None
        """
        cases = [[0, 0], [0, 1], [1, 0], [1, 1]]
        labels = [[0], [1], [1], [0]]
        self.setup(2, 5, 1)
        
        error = self.train(cases, labels, 100000, 0.05)
        print("model train error:", error)
        
        for case in cases:
            print(self.predict(case))
 
 
if "__main__" == __name__:
    nn = BPNeuralNetwork()
    nn.test()