概率论知识复习_概率论复习

0. 基本概念

  概率本身是没有量纲的。

  实验(experiment)包括了步骤(procedures)、概率模型(model)、观察(observation)。
  结果是实验中可能出现的结果(outcome)。
  样本空间是实验所有可能结果的集合。（Sample Space）简称S。
  事件代表的是对实验结果的某种描述，也可以看成是结果的集合，是样本空间的子集。
  概率就是实验结果符合某事件描述的机会有多大。

  事件空间的本质是set of set，样本空间属于事件空间。概率是个函数，是从事件空间到[0,1]的映射。

  经验分布：·假设$X_1,X_2,\dots ,X_n$为一样本，它总体分布函数为$F$，那么如何由样本确定$F$就是统计学的研究内容。那么如何确定$F$呢？

  最简单的办法就是把样本$X_1,X_2,\dots ,X_n$看成一个随机变量的所有取值，且取每个值的概率为$\frac{1}{n}$，该随机变量的分布就是经验分布，所对应的分布函数$F_n$称为经验分布函数。

  似然函数刻画了参数与数据的匹配程度。如果是连续型随机变量，则$L(\theta )=\prod _{i=1}^{n}f(x_i;\theta )$。

  where $x$ is the observed outcome of an experiment. In other words, when $f(x|\theta )$ is viewed as a function of x with $\theta$ fixed, it is a probability density function, and when viewed as a function of $\theta$ with x fixed, it is a likelihood function.

  正确理解$L(\theta |x)$和$f(x|\theta )$之间的区别：considered as a function of $\theta$ , is the likelihood function (of $\theta$ , given the outcome $x$ of $X$). Sometimes the density function for "the value x of X given the parameter value $\theta$ " is written as $f(x|\theta )$. The likelihood function, $L(\theta |x)$, should not be confused with $f(x|\theta )$; the likelihood is equal to the probability density of the observed outcome, x, when the true value of the parameter is $\theta$ , and hence it is equal to a probability density over the outcome $x$, i.e. the likelihood function is not a density over the parameter $\theta$ . Put simply, $L(\theta |x)$is to hypothesis testing, finding the probability of varying outcomes given a set of parameters defined in the null hypothesis; as $f(x|\theta )$ is to inference, finding the likely parameters given a specific outcome。

• Why do people use $L(\theta |x)$ for likelihood instead of P(x|θ)?

  • In this context, it reminds us that the likelihood function is a function of $\theta$ with the data x fixed. On the other hand, the joint distribution is a function of the data x given $\theta$

1. 概率计算

1.1 图解复杂概率问题

  范例：兄弟情。明、华兄弟情笃。故决定一人放弃追求小美以免伤情谊。于罐中放入两白球、一黑球。游戏规则如下：猜拳决定谁先，之后轮流罐中取球；每次可取一至二球，直至有人抽中黑球为止(不放回取球)。抽中黑者退出追求。

  已知猜拳输赢机率为0.5，每次明取球取一颗之机率为0.4，取两颗机率为0.6 。每次华取球取一颗之机率为0.7，取两颗机率为0.3。问最后小明退出追求之机率为？

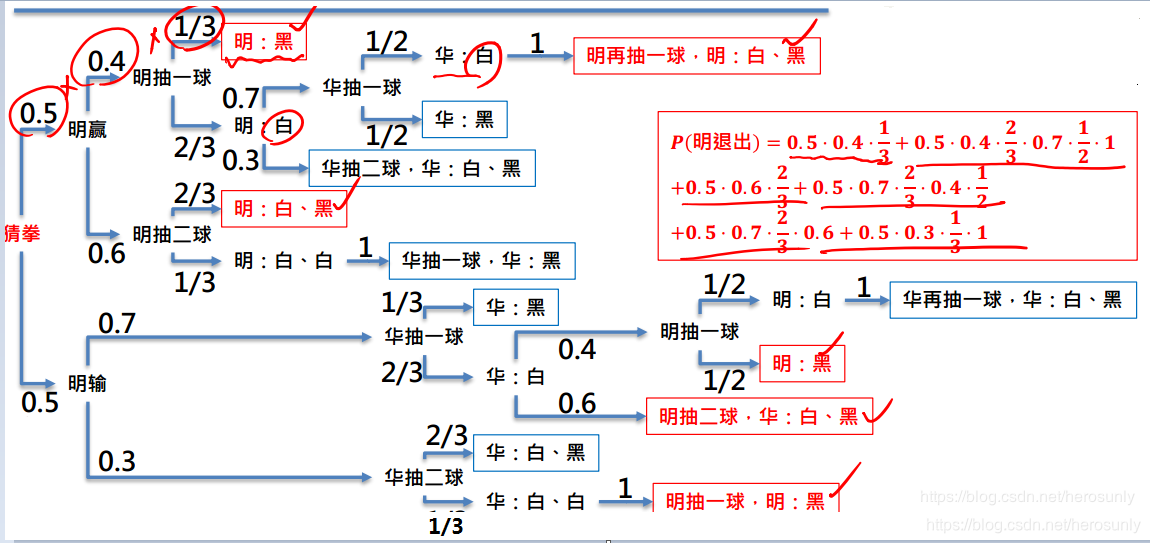
2. 随机变量

  随机变量不是变量，而是实验结果的函数。它是把实验结果进行数字化的函数。$X:S\to R$

2.1 随机变量的种类

  随机变量分为离散型随机变量和连续性随机变量。离散型随机变量指的是随机变量的值是有限个或者可数的无穷多个。

2.1.1 可数和不可数

  一个集合若是不可数的，这代表它包含的东西是无法可以一个个被数的。不管用什么方法数它里面的东西，它里面一定有一样东西是你没数到的！

  第 N位数字定为“9 −第 N 个被数数字的第 N位数字

2.2 二维离散型随机变量的分布律

  我们称 P { X = x i , Y = y j } = p i j , i , j = 1 , 2 , … P\{X=x_i, Y=y_j\}=p_{ij},i,j=1,2,\dots P{X=xi​,Y=yj​}=pij​,i,j=1,2,…为二维离散型随机变量$(X,Y)$的分布律,或随机变量$X$和$Y$的联合分布律。

2.3 高阶矩

  设$X$为随机变量，$c$为常数，$k$为正整数。则量$E[(x-c{)}^k]$为X关于$c$点的$k$ 阶矩。

  当$c=E(X)$，则${\mu }_k=E[(X-E(X){)}^k]$称为$X$的$k$阶中心矩。

  其中${\mu }_3$去衡量分布是否有偏。设$X$的概率密度为$f(x)$，若$f(x)$关于某点$a$对称，即：
$$f(a+x)=f(a-x)$$

  则$E(X)=a$，且${\mu }_3=0$。如果${\mu }_3>0$，则称分布为正偏或右偏。如果${\mu }_3<0$，则称分布为负偏或左偏。特别地,对正态分布而言有${\mu }_3=0$，故如${\mu }_3$显著异于0，则是分布与正态有较大偏离的标志。由于3的因次是X的因次的三次方，为抵消这一点，以$X$的标准差的三次方，即${\mu }_2^{\frac{3}{2}}$去除${\mu }_3$，其商：
$${\beta }_1={\mu }_3/{\mu }_2^{\frac{3}{2}}$$

称为$X$或其分布的“偏度系数”。

  用${\mu }_4$去衡量分布(密度)在均值附近的陡峭程度。因为${\mu }_4=E[(X-E(X){)}^4]$。容易看出，若X取值在概率上很集中在$E(X)$附近，${\mu }_4$则将倾向于小，否则就倾向于大，为抵消尺度的影响，类似于${\mu }_3$的情况。以标准差的四次方即${\mu }_2^2$去除,得
$${\beta }_2=u_4/u_2^2$$

称为$X$或其分布的“峰度系数”。

  “峰度”这个名词，单从表面上看，易引起误解。例如，我们在例2.4中已指出，并由图3.3看出，就正态分布$N(\mu ,{\sigma }^2)$而言,${\sigma }^2$愈小，密度函数在$\mu$点处的“高峰”就愈高且愈陡峭，那么，为何所有的正态分布又都有同一峰度系数?这岂不与这个名词的直觉含义不符?原因在于：${\mu }_4$在除以${\mu }_2^2$后已失去了因次。即与X的单位无关，或者换句话说,两个变量X、Y，谁的峰度大，不能直接比其密度函数，而要调整到方差为1后再去比。也就是说，找两个常数$c_1$和$c_2$，使$c_{1}X$和$c_{2}Y$的方差都为1，再比较其密度的“陡峭”程度如何。

  在这个共同的标准下，“峰度”一词就好理解了。不信看下图。为便于理解，我们在图中画了两条都以p为对称中心的对称密度曲线，且峰的高度一样,但$f_2$在顶峰处很陡，而$f_1$则在顶峰处形成平台，较为平缓。这样，在$\mu$附近，$f_1$的概率多而$f_2$的概率少。而方差都为1，故$f_2$的“尾巴”必比$f_1$的尾巴厚一些，这就导致了${\mu }_4$较大，即有较大的峰度系数。

3. 概率论和数理统计的关系是什么？

  概率论是数理统计的基础，而数理统计是概率论的应用。数理统计是通过采集数据、数据分析、得出尽可能正确的结论。其中数据分析指的是选择模型和参数估计。而选择模型和参数估计就会用到概率论。

3.1 为什么得到的是尽可能正确的结论

  采集数据本质上是对总体进行采样，只有数据量解决无穷大才能得到正确的结论。而样本数量有限，就会使得结论有误差，但我们要得到尽可能正确的结论（前提是每个样本被采样的概率相等）。

  得到结论后，我们需要对结论进行进一步判断，接受或者拒绝该结论。但可能会出现两个问题，以灯泡寿命问题为例，得到了样本平均值$\overline{X}$，将$\overline{X}$和指定数$l$进行比较，从而接收或者拒绝这批灯泡。

  但可能会出现两个问题，在进行假设检验时提出原假设和备择假设，原假设实际上是正确的，但我们做出的决定是拒绝原假设，此类错误称为第一类错误。原假设实际上是不正确的，但是我们却做出了接受原假设的决定，此类错误称为第二类错误。

4. 一维随机变量

4.1 离散型随机变量

  设某事件A在一次试验中发生的概率为$p$，现把这个试验独立地重复$n$次，$X$为$n$次试验中$A$发生的次数，则$X$可取$0,1,\dots n$等值。为确定其概率分布，考虑事件 { X = i } \{X=i\} {X=i}。要这个事件发生，必须在这$n$次试验的原始记录
$$AA\overline{A}\dots \overline{A}A\overline{A}$$

中，有$i$个$A$，$n-i$个$\overline{A}$，每个$A$有概率$p$，而每个$\overline{A}$有概率$1-p$。

4.2 在极限状态下二项分布逼近于泊松分布

5. 数学期望

  数学期望并不改变原有量的量纲，并且它(数学期望)的应用是极其广泛的，比如信息熵就是信息量的数学期望、交叉熵也算是信息量的数学期望(只是内外概率不一致)、KL散度算是概率之比的数学期望。

  设Z是随机变量$X、Y$的函数（g是连续函数）$Z=g(X,Y)$，Z是一个一维随机变量，二维随机变量（$X，Y$）的概率密度为$f(x,y)$，则有：
$$E(Z)=E(g(X,Y))=\int \int g(x,y)f(x,y)dxdy$$
https://www.cc.gatech.edu/~hic/8803-Fall-09/Schedule.html

5.1 方差

$$D(X)=E[(X-E(X){)}^2]$$

$$D(X)=E(X^2)-[E(X){]}^2$$

  需要注意的是，方差是一个差值，并且它的量纲对应的是平方。涉及到两种运算，一个是数学期望，一个是平方运算。很显然的是，先进行平方再进行数学期望的值会更大。也就是二阶中心矩会大于一阶中心距的平方。

6. 定义

6.1 条件概率

6.2 边缘概率

6.3 独立

6.4 相关系数

7. 推论

$p(xyzabc|p)=p(c|p)\ast p(b|cp)\ast p(a|bcp)\ast p(z|abcp)\ast p(y|zabcp)\ast p(x|yzabcp)$

  条件概率与边缘概率结合：

1. $\sum _{y}p(y|x)=1$
2. $\sum _{y}p(xy|z)=p(x|z)$
3. $\sum _{y}p(x|yz)\ne p(x|z)$

  条件概率与独立结合，其中x与y相互独立：

1. $p(xy|z)\ne p(x|z)\ast p(y|z)$
2. $p(x|yz)\ne p(x|z)$

7.1 Jensen不等式

  假设f(x)是凸函数，那么$E[f(x)]\ge f(E(x))$。

8. 复合函数的概率密度函数的证明

  先考虑一个变量的情况：设X有密度函数$f(x)$.设$Y=g(x)$,$g$ 是一个严格上升的函数，即当$x_1<x_2$时,必有$g(x_1)<g(x_2)$.又设g的导数$g^{\prime }$存在.由于g的严格上升性,其反函数$X=h(Y)$存在,且$h$的导数$h^{\prime }$也存在.任取实数y.因g严格上升，有：

因为当g严格下降时其反函数h也严格下降，故$h^{\prime }(y)<0$.这样，$l(y)$仍为非负的.总结(4.2)和(4.3)两式,得知在g严格单调(上升、下降都可以)的情况下,总有$g(X)$的密度函数$l(y)$为：