差分算法介绍

一、一维差分基本概念
差分算法是前缀和算法的逆运算，可以快速的对数组的某一区间进行计算操作。
例如，有一数列 a[1],a[2],.…a[n]，且令 b[i] = a[i]-a[i-1],b[1]=a[1]，那么就有
a[i] = b[1]+b[2]+.…+b[i] = a[1]+a[2]-a[1]+a[3]-a[2]+.…+a[i]-a[i-1]，此时b数组称作a数组的差分数组
，换句话来说a数组就是b数组的前缀和数组 例：
原始数组a：9 3 6 2 6 8
差分数组b：9 -6 3 -4 4 2
可以看到a数组是b数组的前缀和数组。

知道了差分数组有什么用呢？ 别着急，慢慢往下看。
话说有这么一个问题：
给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c,即 a[l] + c , a[l+1] + c , a[l+2] + c , a[r] + c;
暴力做法是for循环l到r区间，时间复杂度O(n)，如果我们需要对原数组执行m次这样的操作，时间复杂度就会变成O(n*m)。有没有更高效的做法吗? 考虑差分做法。

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i]的修改，会影响到a数组中从a[i]及往后的每一个数。
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c;
然后我们打个补丁，b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,a[n] - c;

b[l] + c，效果使得a数组中 a[l]及以后的数都加上了c(红色部分)，但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分)，这样对于a[r] 以后区间的数相当于没有发生改变。

那么现在有一个任务：对数组a区间[left,right]每个元素加一个常数c。这时可以利用原数组就是差分数组的前缀和这个特性，来解决这个问题。对于b数组，只需要执行

b[left] += c, b[right+1] −= c

如果知道a数组的大小，要求b数组，可以通过b[i] = a[i] - a[i-1]来求。也可以通过下面的insert函数还求。
可以这样看来，a数组一开始为全0数组，b数组是a的差分，然后a数组中一个数一个数的插入进来。对于第一个数a[1]的插入，就是在[1,1]的区间段加上a[1]，而对b数组而言，就是b[1]+a[1]，b[1+1]-a[1]，即insert（1，1，a[1]）

void insert(int l , int r , int x){
    b[l] += x;
    b[r + 1] -= x;
}
1
2
3
4

例题：

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

源码:

#include <iostream>

using namespace std;

const int N = 100010;

int n,m;
int a[N], b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r+1] -= c;
}
int main()
{
    scanf("%d %d", &n,&m);
    for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
    for(int i = 1; i <= n; i++) insert(i, i, a[i]);
    while(m--) {
        int l,r,c;
        scanf("%d %d %d", &l,&r,&c);
        insert(l,r,c);
    }
    for(int i = 1; i <= n; i++) a[i]=a[i-1]+b[i];
    for(int i = 1; i <= n; i++) printf("%d ",a[i]);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

二、二维差分基本概念
如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。

a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组

原数组： a[i][j]

我们去构造差分数组： b[i][j]

使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

如何构造b数组呢？

我们去逆向思考。

同一维差分，我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作，可以由O(n*n)的时间复杂度优化成O(1)

已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角，以(x2,y2)为右下角所围成的矩形区域;

始终要记得，a数组是b数组的前缀和数组，比如对b数组的b[i][j]的修改，会影响到a数组中从a[i][j]及往后的每一个数。

假定我们已经构造好了b数组，类比一维差分，我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c

b[x1][y1] + = c;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c
1
2
3
4
5
6
7

每次对b数组执行以上操作，等价于：

for(int i=x1;i<=x2;i++)
  for(int j=y1;j<=y2;j++)
    a[i][j]+=c;
1
2
3

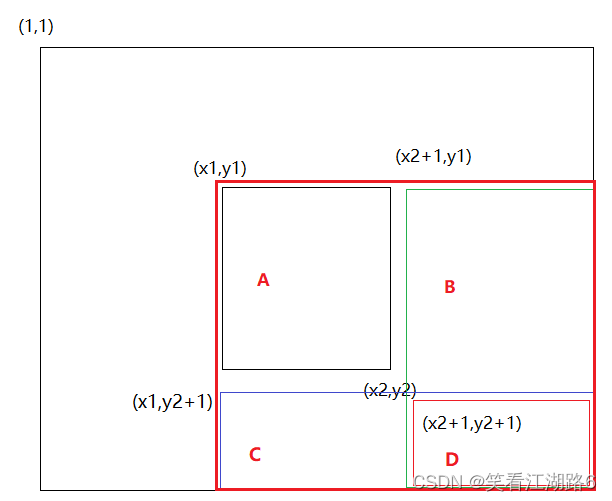
b[x1][ y1 ] +=c ; 对应中最大红色框,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; 对应图中C区域 ,让整个a数组中紫色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图中B区域 ,让整个a数组中绿色矩形面积的元素再减去c，使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图中D区域,让整个a数组中红色矩形面积的元素再加上c，红色内的相当于被减了两次，再加上一次c，才能使其恢复。
我们将上述操作封装成一个插入函数:

void insert(int x1,int y1,int x2,int y2,int c)
{     //对b数组执行插入操作，等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
1
2
3
4
5
6
7

我们可以先假想a数组为空，那么b数组一开始也为空，但是实际上a数组并不为空，因此我们每次让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j]，等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作，就成功构建了差分b数组.
这叫做曲线救国。

for(int i=1;i<=n;i++)
  {
      for(int j=1;j<=m;j++)
      {
          insert(i,j,i,j,a[i][j]);    //构建差分数组
      }
  }
1
2
3
4
5
6
7

例题：

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

解答：

#include<iostream>
#include<stdio.h>

using namespace std;

const int N = 1010;

int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x2+1][y2+1] += c;
    b[x1][y2+1] -= c;
    b[x2+1][y1] -=c;
    return;
}

int main()
{
    int n,m,q;
    scanf("%d%d%d", &n,&m,&q);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]);      //构建初始化b的差分数组
        }
    }
    while(q--) {
        int x1,y1,x2,y2,c;
        cin >> x1 >> y1 >> x2 >> y2 >>c;
        insert(x1, y1, x2, y2, c); //
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            a[i][j] = a[i-1][j]+a[i][j-1]-a[i-1][j-1] + b[i][j];
        }
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            printf("%d ", a[i][j]); //输出
        }
        printf("\n");
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52