数据报告分享|WEKA贝叶斯网络挖掘学校在校人数影响因素数据分类模型

全文链接：https://tecdat.cn/?p=33159

本文着眼普通高等学校在校学生人数,提出了不同种类学校的在校人数可能存在的影响关系从而探究教育现状的因素,建立分类模型,探求这几个因素间的数量关系（点击文末“阅读原文”获取完整代码数据）。

相关视频

本文试图帮助客户通过研究不同种类学校的在校人数的关系，从而挖掘出学校在校人数对技校在校人数是否有影响。

问题分析

本次选取来自广东省统计年鉴1978年以来的各级各类学校在校学生数数据（查看文末了解数据免费获取方式）。

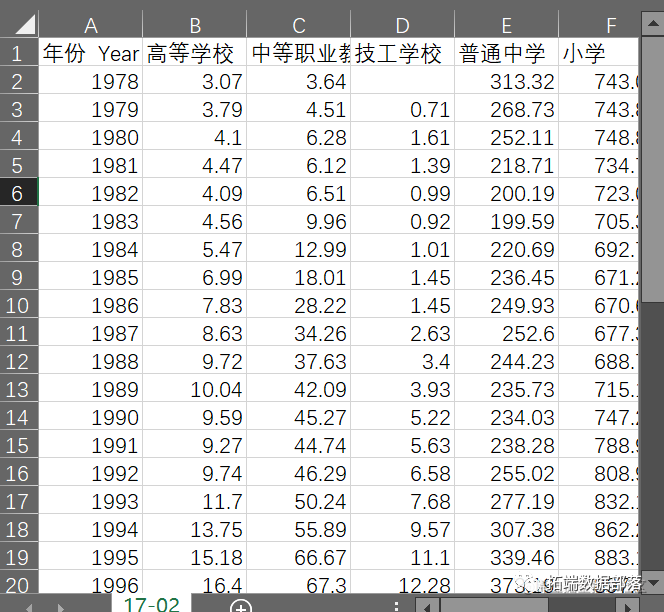
并对高等学校、中等职业教育学校  、技工学校、  普通中学、小学的人数进行贝叶斯分类分析，试图通过分类分析得到不同学校类型在校人数之间存在的关系，从而得出结论，提出建议。

WEKA 使用流程

WEKA使学习应用机器学习方便，高效和乐趣。这是一个GUI工具，它允许您加载数据集，运行算法设计及运行试验与统计结果。

1. 进入软件

    启动Weka的。这可能涉及发现它在程序启动或双击该文件weka.jar。这将启动GUI的Weka选配。

Weka的GUI选择器可以让你选择资源管理器中，实验者，KnowledgeExplorer和简单CLI（命令行界面）中的一个。

2. 加载数据

    该GUI让您加载数据集，运行分类算法。它还提供了其他的功能，如数据过滤，聚类，关联规则提取和可视化，但现在我们不会使用这些功能的。

    点击“打开文件...”按钮，打开“数据”目录中的数据集并双击。

    WEKA提供了一些常见的小机器学习数据集，你可以用它来练习上。

---

点击标题查阅往期内容

课程视频|R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例

左右滑动查看更多

01

02

 

03

04

3. 进行挖掘

    现在你已经加载的数据集，它的时间来选择一个机器学习算法建模的问题，并作出预测。

    点击“分类”标签。这是用于运行针对Weka的一个装载数据集的算法的区域。

点击“开始”按钮，运行该算法。

数据

本次分析的数据来自广东省统计年鉴的各级各类学校在校学生数数据。《广东统计年鉴》(下简称《年鉴》)系统收录了全省及各市、县(区)在校人数的统计数据,以及1978年以来各个主要时期全省一共221条主要统计数据。

指标选取

本次分析一共选取了5个指标221个样本，分别是：高等学校、中等职业教育学校 、技工学校、  普通中学、小学。

---

贝叶斯网络

贝叶斯网络是一种概率网络，它是基于概率推理的图形化网络，而贝叶斯公式则是这个概率网络的基础。

由乘法公式，我们得到

P (A | B) = P (A, B) / P (B)=(P(B|A)P(A))/P(B)

这就是著名的贝叶斯公式。

贝叶斯公式几乎是所有概率推理的现代人工智能系统的基础。这个式子同样表示一组公式，每个公式处理变量的特定取值。我们还有某些场合要在某个背景证据e上使用一个更通用版本的条件化公式：

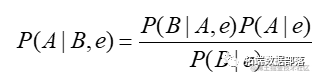
贝叶斯法则是在一个条件概率和2个无条件概率的基础上计算另一个条件概率。

贝叶斯法则对于回答在某一条证据的条件约束下的概率问题是非常有用的，而且我们已经讨论过概率信息经常是以P（结果 | 原因）的形式出现的。

为了解决以上问题，我们利用‘独立性’。

给定第三个随机变量Z（证据）之后，两个随机变量X和Y的条件独立性的一般定义是：

P(X,Y|Z)=P(X|Z)P(Y|Z)

也可以用以下形式来表示

P(X|Y,Z)=P(X|Z)

P(Y|X,Z)＝P(Y|Z)

因此对于前面讲过的决对独立断言，允许将全联合分布分解成很多更小的分布，对于条件独立性断言也是同样成立的。

通过条件独立性，将一个大的概率领域分解城一些相互联系非常弱的子集，并允许概率系统进行规模扩展，而且条件独立性也比决对独立性断言更加普遍，称为素贝叶斯模型。

数据准备：

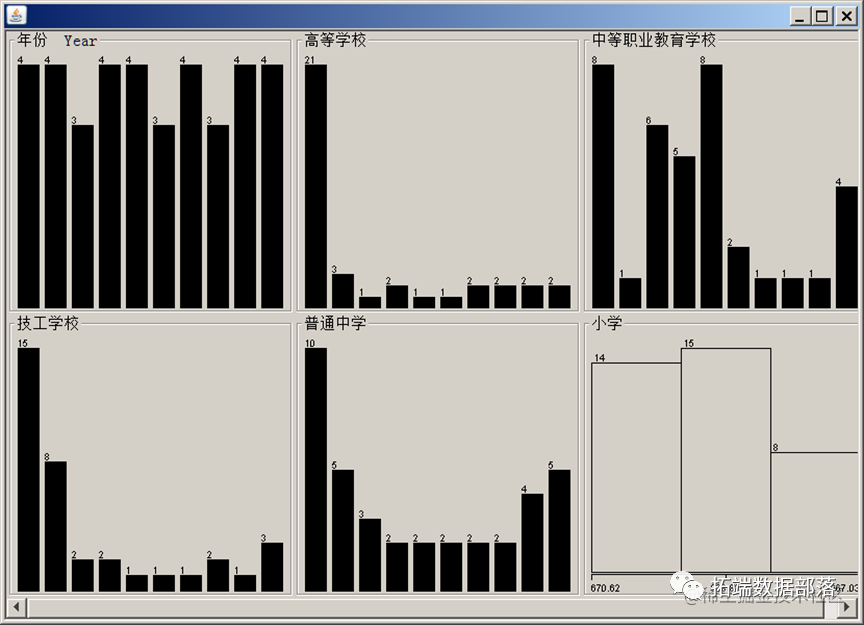
首先在weka中打开数据

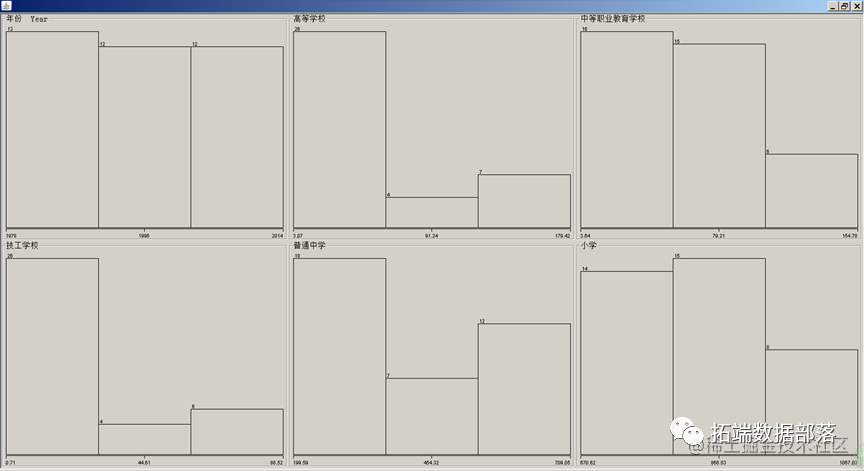
查看每个学校的人数分布直方图

数据预处理：

为了消除数据量纲的变化，数据标准化：

然后将数据进行离散化 ，分成几个不同等级：

---

点击标题查阅往期内容

R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型

左右滑动查看更多

01

02

03

04

贝叶斯模型训练:

建立贝叶斯模型，训练模型：

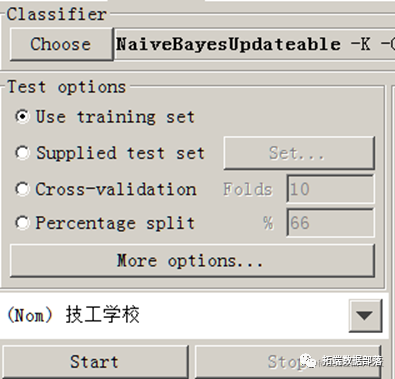
将技工学校的人数作为预测变量

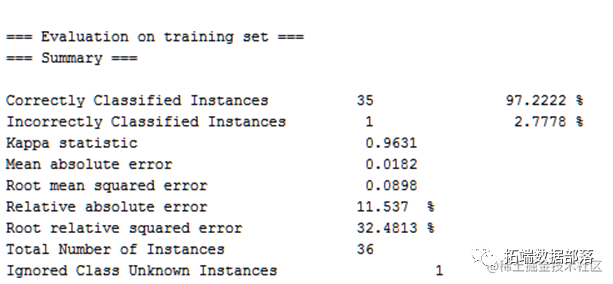
实验结果

十折交叉验证

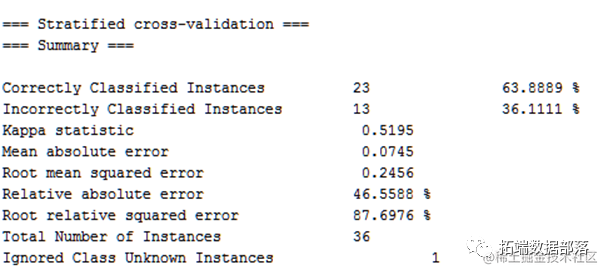
方法的比较

为了进行对比分析，本文选用准确率(Precision)、召回率(Recall)和覆盖率(Coverage)度量。

推荐结果的召回率定义为：

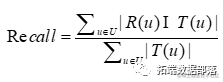
推荐结果的准确率定义为：

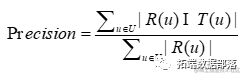
覆盖率(Coverage)描述的是一个推荐系统对物品长尾的发掘能力。推荐系统的覆盖率可以通过下面的公式计算：

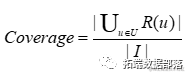
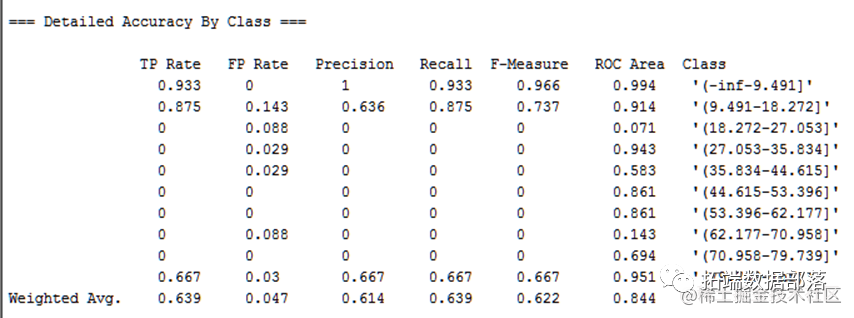
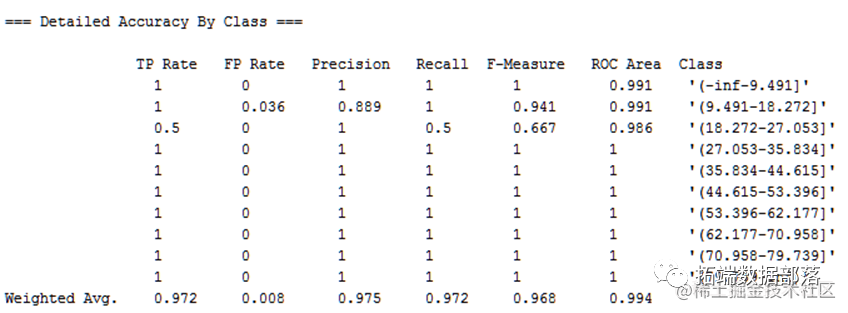
得到每个类别的准确率、召回率、roc等结果：

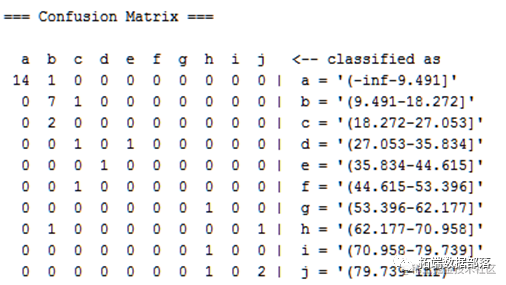
混淆矩阵

对模型进行优化

每个类别的准确度和召回率等信息：

混淆矩阵

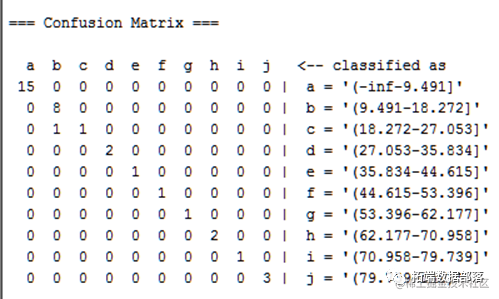
对分类结果进行可视化

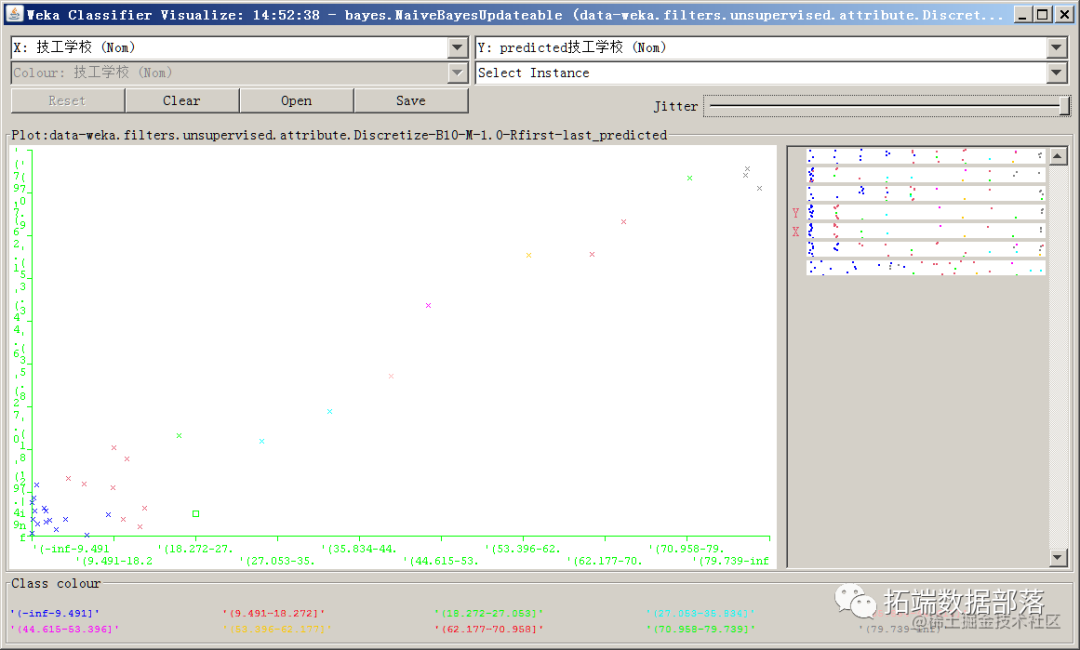
从散点图来看，可以看到不同颜色代表不同技工学校的人数分类。纵轴代表预测人数，横轴代表实际人数。由于预测人数分布在y=x的直线上，因此可以认为预测人数等于实际人数，说明模型的预测效果良好。

由上图的比较可以看到，本文使用核函数进行改进后的方法的统计指标均明显优于各个子预测方法，准确度分别提高了 34%，召回率将对于之前算法提高为36% ，总体来说有明显的提高。

结论

从模型的结果来看，不同种类的学校的在校人数之间存在一定的联系。通过贝叶斯网络模型可以利用年份小学，初中等在校人数来预测技校的在校人数的数量，因此长远来看，我们可以通过不同学校的在校人数来预测未来人数的发展趋势。同时说明小学、初中的在校人数会影响技工学校的在校人数，同时技工学校人数和大学在校人数也有关系。高中毕业之后有些人会选择去技工学校学习专业技能，有些人会选择去高校深造，他们之间存在负相关关系，同时良好的初中小学的教育也会影响本科在校人数，因此对学生的义务教育也是相当重要的。

同时，在未来的研究中，还要结合办学条件、教学质量、学校内部结构等方面的因素来对学校的因素进行更深程度的研究。

数据获取

在公众号后台回复“学生数据”，可免费获取完整数据。

本文中分析的数据和报告分享到会员群，扫描下面二维码即可加群！

点击文末“阅读原文”

获取全文完整代码数据资料。

本文选自《数据报告分享|WEKA贝叶斯网络挖掘学校在校人数影响因素数据分类模型》。

点击标题查阅往期内容

课程视频|R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例

PYTHON用户流失数据挖掘：建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像

数据代码分享|R语言lasso回归、贝叶斯分析员工满意度调查数据、缺失值填充

R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型

R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

python贝叶斯随机过程：马尔可夫链Markov-Chain，MC和Metropolis-Hastings，MH采样算法可视化

Python贝叶斯推断Metropolis-Hastings（M-H）MCMC采样算法的实现

Metropolis Hastings采样和贝叶斯泊松回归Poisson模型

Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列

R语言RSTAN MCMC：NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据

R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析

R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型

R语言贝叶斯MCMC：用rstan建立线性回归模型分析汽车数据和可视化诊断

R语言贝叶斯MCMC：GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例

R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数

R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数

R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病

R语言中贝叶斯网络（BN）、动态贝叶斯网络、线性模型分析错颌畸形数据

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

Python贝叶斯回归分析住房负担能力数据集

R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析

Python用PyMC3实现贝叶斯线性回归模型

R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型

R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

R语言和STAN,JAGS：用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据

R语言基于copula的贝叶斯分层混合模型的诊断准确性研究

R语言贝叶斯线性回归和多元线性回归构建工资预测模型

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言stan进行基于贝叶斯推断的回归模型

R语言中RStan贝叶斯层次模型分析示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

视频：R语言中的Stan概率编程MCMC采样的贝叶斯模型

R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计