知新_RL

这个屌丝很懒，什么也没留下！

热门标签

【动态规划】背包问题题型及方法归纳

作者：知新_RL | 2024-04-04 03:47:15

踩

背包问题

背包问题的种类

背包问题是在规定背包容量为j的前提下，每个物品对应的体积为v[i]，价值为w[i]，从物品0到物品i中选择物品放入背包中，找出符合某种要求的价值。

（1）背包问题种类

01背包：每种物品只能选择1个。
完全背包：每种物品可以选择无限个。
多重背包：每种物品最多可选s[i]个。
分组背包：有若干个组，每组内有若干个物品，每个物品只能选一次。

（2）递推公式

01背包：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])
完全背包：dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
多重背包：dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i], dp[i - 1][j - 2 * v[i]] + w[i] + ... + dp[i - 1][j - s[i] * v[i]] + s[i] * w[i])
分组背包：dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i][k] + w[i][k], + ... + dp[i - 1][j - s[i]*v[i][k]] + s[i] * w[i][k])

（3）滚动数组遍历顺序：
遵循原则：用到上一层的信息i-1，则从大到小遍历；用到本层的信息i，则从小到大遍历。

01背包：从大到小
完全背包：从小到大。组合问题：先物品，再背包。排列问题：先背包，再物品。
多重背包：在01背包的基础上，用到i-1层信息，从大到小，多一层for循环选物品个数
分组背包：在01背包的基础上，用到i-1层信息，从大到小，多一层for循环选物品个数

（4）初始化问题：

要求恰好装满：dp[i][0] = 0， dp[j] = -∞ （j ≠ 0）
要求恰好装满：dp[i][0] = dp[j] = 0

可以这样理解：初始化的dp数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可以在什么也不装且价值为0的情况下被“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，应该被赋值为-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。

（5）题型特点

01背包：已给数组中可用元素固定且每次只能用一次，限制容量固定（可能会存在多重背包容量）。

1、01背包问题

主要分为两部分：状态表示和状态计算。

1. 状态表示dp[i][j]
i是物品个数，j是条件限制。状态表示一般从两个角度考虑，分别为集合和属性。
其中，集合是只考虑前i个物品，不超过j的选法集合。属性值的是数量、最大值、最小值等。当要求的数到达某一个值时，就要求j - v[i]到达那个相应的值时，会更新，这就要求设置好初始值，一般会让dp[i][0]=0或dp[i][0]=1。

2. 状态计算
状态计算主要是集合划分，分为 f(i-1, j) 所有不选第i个物品的方案和所有选择第i个物品的方案，这种方式可保证不遗漏和不重复。

（1）不超过j的条件下，对于所有不选第i个物品的方案
因为是对i从0开始按顺序遍历，因此选择的是从0-i-1中的选择方案。

（2）不超过j的条件下，所有选择第i个物品的方案
此集合包含两个部分，一个是含有第i个物品，另一个是不含第i个物品从0-i-1中选择的方案。含有第i个物品时，表示的是物品i的体积v[i]为唯一的定量。不含第i个物品时，条件就变为j - v[i]，减去了第i个物品的体积，在此条件下，从0-i-1中选，此时会有多种方案，为变量。按我们的目标要求，如果要找最大值，就从多种方案中的一个最大值方案，如果要找最小值，就从多种方案中的最小值方案。两个部分相加，就是我们此方案的结果。

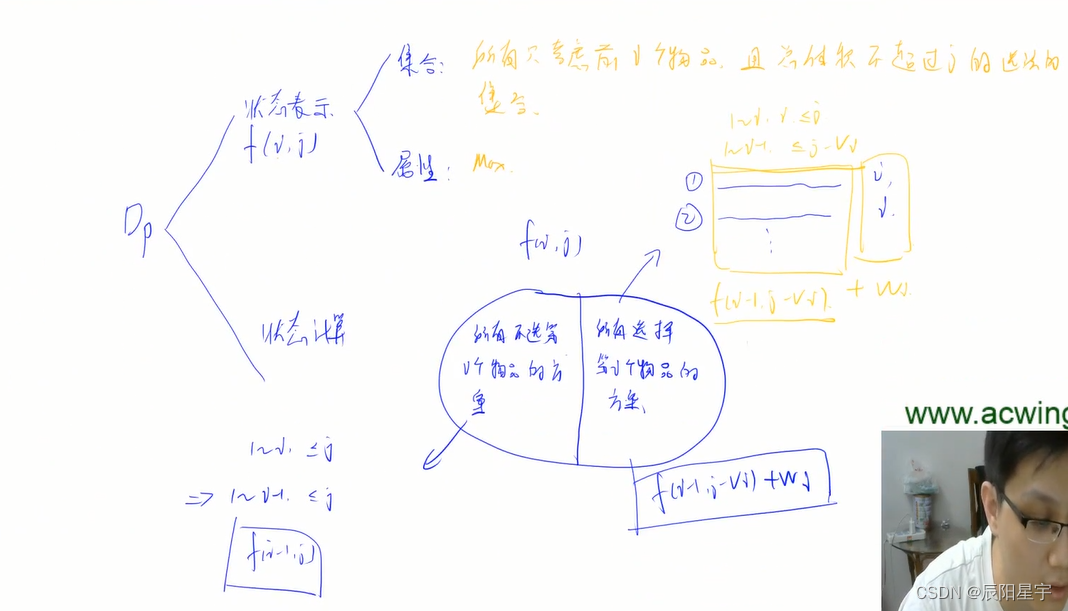
在这里插入图片描述
dp[i][j]二维数组

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int dp[N][N];

int main(){

    int n, m;
    int v[N], w[N];
    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            // 当前物品重量大于背包容量时，不放该物品
            if(j < v[i])        dp[i][j] = dp[i - 1][j];
            // 当前物品重量小于等于背包容量时，在放该物品后和不放该物品之间选择一个最大价值
            else                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
        }
    }
    
    cout << dp[n][m] << endl;
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

dp[j]一维滚动数组
将dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])改为等价式dp[j] = max(dp[j], dp[j - v[i]] + w[i])，遍历顺序改变为从大到小，通常会初始化dp[0]=0或dp[o]=1。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
int dp[N];

int main(){

    int n, m;
    int v[N], w[N];
    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        // 从后向前遍历，表示装入一个物品后，剩余的可装入容量达到的最大价值
        for(int j = m; j >= v[i]; j--) {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

151、【动态规划】leetcode ——2. 01背包问题（C++版本）：二维数组+滚动数组

拓展应用：

152、【动态规划】leetcode ——416. 分割等和子集：滚动数组+二维数组（C++版本）：将重量之和除以2，作为背包容量，找到能让背包中可装物体体积最大的装发，让背包中装入物品的重量等于背包容量。
【动态规划】leetcode ——1049. 最后一块石头的重量 II：滚动数组（C++版本）：思路与上一题相同，分割成两个数量相近的集合，最后两个集合的综合相减。
154、【动态规划】leetcode ——494. 目标和：回溯法+动态规划（C++版本）：分割成正数集合和负数集合，背包容量为正数集合大小，找到可组成正数集合大小的组合方式。
155、【动态规划】leetcode ——474. 一和零：三维数组+二维滚动数组（C++版本）：字符串作为物品，m个0和n个1作为背包容量（具有多重背包）。

2、完全背包问题

与01背包的区别在于同一个物品可以有无限个，对同一个物品可选择多次。

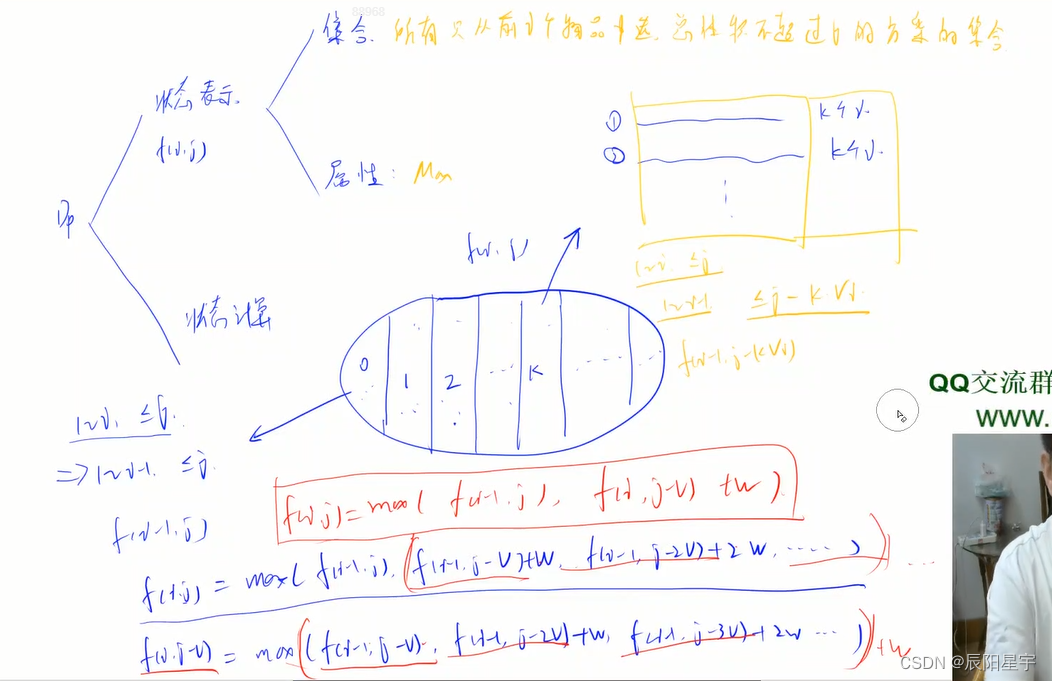
在这里插入图片描述

状态计算时，在dp[i][j]情况下 ，划分集合时01背包只能 划分成两个集合 ，而完全背包可以划分为多个集合（第i个物品选择0个、1个、2个…一直到体积达到或超过j为止的多种方案），其中选择0个时，就相当于在0-i-1中选择的方案dp[i - 1][j]。

递推公式表达式为：
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + 2*w[i] + ... + dp[i - 1][j - n*v[i]] + n*w[i])（n*v[i]刚好小于等于j）

现在来进行简化，由上式可知，dp[i][j - v[i]] = max(dp[i - 1][j - v[i]], dp[i - 1][j - 2*v[i]] + w[i] + ... + dp[i - 1][j - n*v[i]] + (n-1)*w[i])，对该式两端加上一个w再联立第一个式子，从而得最终简化式子：

dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])

dp[i][j]二维数组

#include <iostream>

using namespace std;

const int N = 1010;
int dp[N][N];
int v[N], w[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++)      cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1;j <= m; j++) {
            if(v[i] > j)        dp[i][j] = dp[i - 1][j];
            else                dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
        }
    }
    
    cout << dp[n][m] << endl;
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

d[j]一维滚动数组
滚动数组的遍历顺序按照从小到大遍历。

#include <iostream>

using namespace std;

const int N = 1010;
int dp[N];
int v[N], w[N];
int n, m;


int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++)      cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = v[i]; j <= m; j++) {
            // dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

156、【动态规划】AcWing ——3. 完全背包问题：二维数组+一维滚动数组（C++版本）

拓展应用：
完全背包中，会牵扯两个不同的问题：组合问题和排列问题。对于组合问题，就是规定一批相同的元素，不同的排列代表同一个结果。而排列问题，就是规定一批相同的元素，不同的排列代表不同的结果。为了实现这两个问题，通常会让组合问题遍历顺序是先遍历物品，再遍历背包，这样子可以让dp只记录某一结果中的一种情形仅被记录。而排列问题遍历顺序是先遍历背包，再遍历物品，这样子可以让dp记录所有的排列出现的情况。

例如，[1, 3]和[3, 1]，在组合问题中只记录了[1, 3]这种情况即可。而在排列问题中，[1, 3]和[3, 1]都被记录了下来。
先遍历物品，再遍历背包，会让某一物品，在各个容量的情况下按物品放入顺序被唯一确定下来放还是不放。
先遍历背包，再遍历物品，会让在不同容量下，都将各个物品从头遍历了一遍，就会得到所有的排列情况。

无顺序要求的题目：

159、【动态规划】leetcode ——322. 零钱兑换：二维数组+一维滚动数组（C++版本）：注意求最小值的初始化，由于不考虑顺序问题，因此遍历顺序都可以，dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i]])。
160、【动态规划】leetcode ——279. 完全平方数：二维数组+一维滚动数组（C++版本）：方式同上，递推公式用上完全平方数形式，dp[i][j] = min(dp[i - 1][j], dp[i][j - i * i] + 1)。

（1）组合问题

数组中元素相同、顺序不同视为同一个结果，组合问题遍历顺序按先物品，再遍历背包。

158、【动态规划】leetcode ——518. 零钱兑换 II：二维数组+一维滚动数组（C++版本）：零钱可以多次使用不考虑数字顺序位置关系，累加计算dp[i][j] = dp[i - 1][j] + dp[i][j - v[i]]。
191、【动态规划】AcWing ——AcWing 900. 整数划分：完全背包解法+加减1解法（C++版本）：dp[i][j] = (dp[i - 1][j] + dp[i][j - i])，从1~n中选数，组合成总额和为j的方案个数。

（2）排列问题

数组中元素相同、顺序不同视为不同结果，排列问题遍历顺序按先背包，再遍历物品。最内层再加上一个从0-i再遍历探寻各种情况的for循环。

158、【动态规划】leetcode ——377. 组合总和 Ⅳ（C++版本）：数字可以多次使用考虑数字顺序位置关系，一维滚动数组累加计算dp[j] += dp[j - v[i]]，二维比较特别sum(dp[i][j], dp[i][j - nums[k])，内层需要从0-i再遍历一次。
145、【动态规划】leetcode ——70. 爬楼梯：暴力法+动态规划（C++版本）：完全背包解法与题2相同，也是排列问题。
161、【动态规划】leetcode ——139. 单词拆分：回溯法+动态规划（C++版本）：这个题比较奇特一些，当满足前面的字符可以被组成并且当前单词可以有字典中组成时，为dp[j] = true

3、多重背包问题

多重背包是对每种物品的数量进行限制，dp[i][j]的意思：在第i种物品的个数为规定s[i]个的前提下，背包容量为j，物品体积为v[i]，从物品0到物品i中选择物品，可达到的最大价值。

实现方式是在01背包实现的基础上，遍历时候，在最内层设置一个for循环，寻找从一个都不选到选s[i]个第i个物品时，哪种情况取得最大价值。

dp[i][j]二维数组

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int dp[N][N];
int v[N], w[N], s[N];


int main() {
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            // 一个都不选一直到选s[i]个，选择一种最大价值情况
            for(int k = 1; k <= s[i] && j >= k * v[i] ; k++) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
    
    cout << dp[n][m] << endl;
    
    return 0;
    
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

d[j]一维滚动数组

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int dp[N];
int v[N], w[N], s[N];


int main() {
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++)         cin >> v[i] >> w[i] >> s[i];
    dp[0] = 0;
    
    for(int i = 1; i <= n; i++) {
        for(int j = m; j >= 0; j--) {
            // 一个都不选一直到选s[i]个，选择一种最大价值情况
            for(int k = 0; k <= s[i] && j >= k * v[i] ; k++) {
                dp[j] = max(dp[j], dp[j - k * v[i]] + k * w[i]);
            }
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
    
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

162、【动态规划】AcWing ——4. 多重背包问题 I（C++版本）

4、分组背包

分组背包问题是在01背包的基础上，多了一个组的概念。有若干个组，每组里面有若干个物品，每个物品只能选择一次，找到在背包容量为j的前提下，从0-i组中选择物品，达到背包里价值最大。

d[j]一维滚动数组

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int dp[N];
                    
int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        cin >> s[i];
        for(int j = 0; j < s[i]; j++) {
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for(int i = 1; i <= n; i++) {                   // 遍历物品
        for(int j = m; j >= 1; j--) {               // 从大到小，遍历背包（使用i-1层信息）
            for(int k = 0; k < s[i]; k++) {         // 遍历每组内的物品个数
                if(j >= v[i][k]) {
                    dp[j] = max(dp[j], dp[j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    
    cout << dp[m] << endl;
    
    
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

166、【动态规划】AcWing ——9. 分组背包问题（C++版本）

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/357226