- 1微信小程序 实现在底图上绘制扇形_原生微信小程序如何画扇形图表
- 2AlexNet基于MNIST数据集的代码实现_alexnet mnist
- 3Spring Shiro基础组件 SecurityManager_spring securitymanager
- 46月1日,今日信息差
- 5时序违例在FPGA开发流程的分析及解决,结合实际工程_片内时序违例
- 6【Python学习笔记】Python实现文件批量转为utf-8格式_python批量转换utf8
- 7新型Black Matter勒索病毒,勒索300万美金_blackmatter
- 8最新VS code配置C/C++环境(tasks.json, launch.json,c_cpp_properties.json)及运行多个文件、配置Cmake_配置c_cpp_properties.json
- 9vscode使用git_vscode集成git
- 10微服务之SpringCloud AlibabaSeata处理分布式事务
密码学《图解密码技术》 记录学习 第十五章
赞
踩
目录
十五章
15.1本章学习的内容
本章中,我们将对本书的内容做一个总结。
首先,我们来整理一下本书中出现的密码技术,并思考一下密码技术的现状与局限性。接下来,我们将介绍密码技术的应用——虚拟货币比特币,还将简单介绍一下被称为完美的密码技术而备受期待的量子密码和量子计算机。最后,我们将探讨一下“完美的密码技术因为有不完美的人类参与而无法实现完美的安全性”这一话题,并结束整本书的内容。
15.2 密码技术小结
本书中,我们介绍了各种各样的密码技术。本节中我们将复习一下最基本的6种密码技术,并整理一下它们之间的相互关系。
15.2.1 密码学家的工具箱
本书中,我们用“密码学家的工具箱”这一概念反复讲解了 6种基本的密码技术。
对称密码是一种用相同的密钥进行加密和解密的技术,用于确保消息的机密性。在对称密码的算法方面,目前主要使用的是AES。尽管对称密码能够确保消息的机密性,但需要解决将解密密钥配送给接收者的密钥配送问题。
公钥密码是一种用不同的密钥进行加密和解密的技术,和对称密码一样用于确保消息的机密性。使用最广泛的一种公钥密码算法是RSA,除此之外还有ElGamal和Rabin等算法,以及与其相关 Diffie-Hellman 密钥交换(DH)和椭圆曲线 Diffie-Hellman 密钥交换(ECDH)等技术。和对称密码相比,公钥密码的速度非常慢,因此一般都会和对称密码一起组成混合密码系统来使用。公钥密码能够解决对称密码中的密钥交换问题,但存在通过中间人攻击被伪装的风险,因此需要对带有数字签名的公钥进行认证。
单向散列函数是一种将长消息转换为短散列值的技术,用于确保消息的完整性。在单向散列函数的算法方面,SHA-1 曾被广泛使用,但由于人们已经发现了一些针对该算法的理论上可行的攻击方式,因此该算法不应再被用于新的用途。今后我们应该主要使用的算法包括目前已经在广泛使用的 SHA-2 (SHA-224、SHA-256、SHA-384、SHA-512),以及具有全新结构的SHA-3 (Keccak)算法。单向散列函数可以单独使用,也可以作为消息认证码、数字签名以及伪随机数生成器等技术的组成元素来使用。
消息认证码是一种能够识别通信对象发送的消息是否被篡改的认证技术,用于验证消息的完整性,以及对消息进行认证。消息认证码的算法中,最常用的是利用单向散列函数的HMAC。HMAC 的构成不依赖于某一种具体的单向散列函数算法。消息认证码能够对通信对象进行认证,但无法对第三方进行认证。此外,它也无法防止否认。消息认证码也可以用来实现认证加密。
数字签名是一种能够对第三方进行消息认证,并能够防止通信对象做出否认的认证技术。数字签名的算法包括RSA、 ElGamal、 DSA、椭圆曲线DSA ( ECDSA)、爱德华兹曲线DSA(EDDSA)等。公钥基础设施(PKI)中使用的证书,就是对公钥加上认证机构的数字签名所构成的。要验证公钥的数字签名,需要通过某种途径获取认证机构自身的合法公钥。
伪随机数生成器是一种能够生成具备不可预测性的比特序列的技术,由密码和单向散列函数等技术构成。伪随机数生成器用于生成密钥、初始化向量和 nonce等。密码学家的工具箱中的内容可整理成图15-1。
15.2.2 密码与认证
当提到密码技术时,我们往往只会想到密码,但从密码学家的工具箱来看,认证也是非常重要的一部分。
例如,公钥密码是一种很重要的技术,但如果无法确认自己所持有的公钥的合法性,即是否是经过认证的公钥,公钥密码就无法发挥作用。
此外,即便在使用高强度的密码算法来确保机密性的情况下,依然存在像填充提示攻击这样通过伪造密文来窃取明文相关信息的攻击方式。在这种情况下,我们需要对接收到的密文进行认证,判断其是不是通过合法的加密过程生成出来的,这样才能有效地确保信息的机密性。
15.2.3 密码技术的框架化
本书中多次使用了框架这个说法。框架的特点就是能够对其中作为组成元素的技术进行替换。一种元素技术即便再完美,总有一天也会显现出弱点。当出现这样的情况时,只要形成了整体框架,就可以对其中存在弱点的技术进行替换,就像更换损坏的机器零件一样。
例如,消息认证码算法HMAC的设计就允许对单向散列函数的算法进行替换。当发现目前使用的单向散列函数存在弱点时,我们可以用其他的单向散列函数算法重新构建HMAC。
此外,在PGP中,对称密码、公钥密码、单向散列函数等都是可以替换的。在SSL/TLS中,客户端和服务器可以通过握手协议进行通信,并当场决定所使用的密码套件。
使用框架能够提高密码技术系统的重用性,也能够提高系统的强度。这可以说是人类应对未来技术变革的智慧。即便目前所使用的密码算法被破解,也没有必要将现有的系统全部废弃,只要框架本身的设计合理,就可以通过替换更安全的密码算法来解决问题。
通过将单独的密码技术像零件一样组合起来,并根据需要进行替换,能够实现更长期的、更高的安全性。当然,现实世界中的问题也并没有这样单纯。2014年发现的POODLE攻击,就是利用SSL/TLS在握手协议中确定密码套件的机制来对协议的版本进行强制降级的(14.4.3节),这可以说是一种针对 SSL/TLS 框架本身的攻击。
15.2.4 密码技术与压缩技术
下面我们来讨论一个更加有趣的话题。在密码学家的工具箱中,所有的技术都有一个共同点,那就是它们都可以看成是一种“压缩技术”。请看图 15-2。
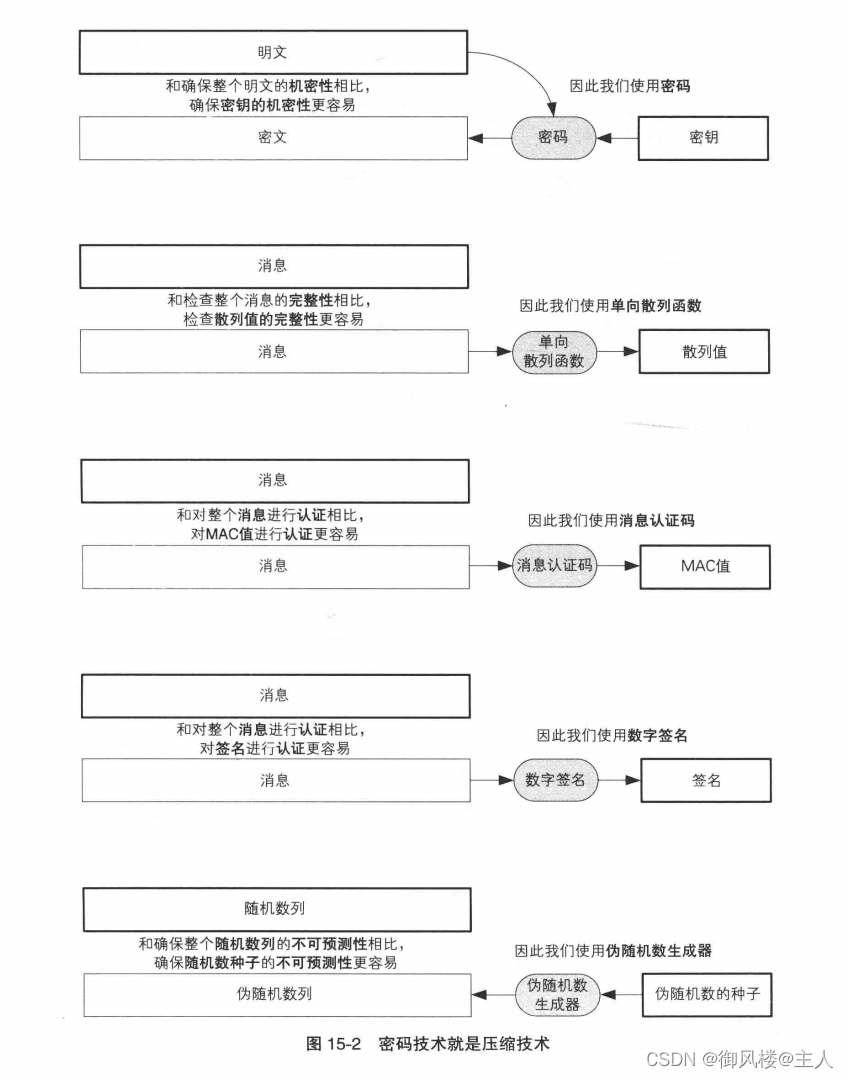
无论是对称密码还是公钥密码,密码的作用都是确保机密性。由于确保较长的明文整体的机密性很困难,因此我们用密码将明文转换成密文。这样一来,我们就不必保护明文本身了。相对地,我们则需要保护加密时所使用的密钥。通过保护较短的密钥来保护较长的明文,这样的做法可以称为机密性的压缩。
单向散列函数是用于确认完整性的。我们不必检查较长的明文的完整性,只要检查散列值就能够确认完整性了。通过检查较短的散列值来确认较长的明文的完整性,这样的做法可以称为完整性的压缩。
消息认证码和数字签名都是用于认证的技术,但我们并不是直接对较长的消息本身进行认证,而是通过将较长的消息与密钥结合起来,生成较短的比特序列(认证符号),再通过认证符号进行认证。在消息认证码中,MAC值就是认证符号;而在数字签名中,签名就是认证符号。通过较短的认证符号来对较长的消息进行认证,这样的做法可以称为认证的压缩。
那么伪随机数生成器又是怎样的呢?在伪随机数生成器中,所生成数列的不可预测性是非常重要的。要大量生成具备不可预测性的随机数列非常困难,于是我们通过将种子输入伪随机数生成器,生成具备不可预测性的伪随机数列。也就是说,为了对伪随机数列赋予不可预测性,我们使用了随机数种子,这可以称为不可预测性的压缩。反过来说,伪随机数生成器是将种子所具备的不可预测性进行了扩张。
这里的观点很重要,因此我们从另一个角度来总结一下。
⚪密钥是机密性的精华
⚪散列值是完整性的精华
⚪认证符号(MAC值和签名)是认证的精华
⚪种子是不可预测性的精华
通过上面的整理,大家应该可以理解密钥、认证符号和种子之间的关系了吧(表 15-1)。

15.3 虚拟货币——比特币
下面我们从技术层面介绍一下近年来备受关注的虚拟货币—-比特币(Bitcoin)。关于比特币在经济层面的影响,有很多著作可以参考。本节的内容参考了最初介绍比特币的论文①,以及比特币基金会(Bitcoin Foundation), Bitcoin.org、Bitcoin Developer Guide等资料。不过,由于比特币本身并不存在官方管理机构,因此上面这些网站都不能算是比特币的官方网站。
15.3.1 什么是比特币
比特币是一种虚拟货币,也叫密码学货币。比特币可以脱离物理介质,仅通过互联网就可以流通,而且其手续费低廉,使得小额交易更加方便。
比特币的实现基于一个自称中本哲史⑤的不明身份的人所发表的一篇论文。比特币于2009年开始被实际运用,随后迅速在世界各国流行起来。2015年,美国开设了世界上第一家比特币交易所 Coinbase.
1 比特币通常写作 1 bitcoin 或者 1 BTC①。表 15-2 中列举了一些零钱的单位,其中0.00000001 BTC称为1 satoshi,这是以比特币原始论文的作者命名的。和其他货币一样,比特币的相对价值也在不断变化, 2015年6月时, 1BTC大约相当于3万日元。

目前有很多网站和服务接受比特币交易,但中国、印度尼西亚、俄罗斯等国家则禁止使用比特币。
日本没有禁止比特币,但根据2014年日本政府出台的意见,比特币在日本不被视作货币,而是被视作商品,因此银行是禁止以主营业务的方式来经营比特币的。此外,和贵金属一样,比特币的交易也需要纳税。
日元是日本的法定货币,但比特币并不是由某个国家来管理的,也没有类似中央银行的组织。因此,信用卡遗失时可以通过银行补办,但比特币交易时使用的私钥一旦遗失,所关联的比特币就再也无法找回了。
15.3.2 P2P 网络
既然比特币体系中没有中央银行,那么市场上的比特币到底是存放在哪里的呢?比特币之所以能够成为一种流通的货币,完全依赖于全世界所有比特币用户组成的 P2P 网络①(Peer toPeer Network)。也就是说,全世界所有比特币用户的计算机(node 或者 peer)共同保存、验证和使用支撑比特币体系的所有必要信息。
与其说比特币是一种货币,不如说比特币是一种基于 P2P 网络的支付结算系统,这样更易于人们理解其本质。比特币用户通过使用比特币这一支付结算系统实现了价值的转移,因此比特币看上去才具备了货币的特征。
15.3.3地址
比特币交易是在比特币地址之间完成的(以下将比特币地址简称为地址)。假设 Alice要从Bob商店购买商品,并通过比特币来支付,流程如下。
⚪Bob 商店生成地址 B
⚪Bob 商店将地址 B 告知 Alice
⚪Alice 生成地址 A
⚪Alice 从地址 A 向地址 B 支付货款
这和 Alice 给 Bob 发一封电子邮件的流程差不多,正如电子邮件需要在两个邮箱地址之间传送一样,比特币的交易也是在两个地址之间进行的。不过,和邮箱地址不同,大多数情况下人们会为每一次比特币交易创建不同的地址。当然,在捐赠等场景中,也会反复使用同一个地址。
比特币中使用的地址是由公钥的散列值生成的。具体来说,将椭圆曲线DSA的公钥输入SHA-256 和 RIPEMD-160两个单向散列函数来求出散列值,为其附加一些信息后再通过Base58Check进行编码,转换成字符串。为了防止混淆, Base58Check编码中不使用数字零(0)、大写O、大写I以及小写i。
例如,维基百科的创始人Jimmy Wales于2014年3月7日在推特上发布了下面这样一个地址。
1McNsCTN26zkBSHs9fsgUHHy8u5S1PY5q3
正如上面的例子所示,比特币公钥生成的地址(Bitcoin pubkey hash)都是以数字“1”开头的。
15.3.4 钱包
发送电子邮件时需要使用电子邮件客户端,比特币交易也是一样,需要使用比特币的客户端,这种客户端称为钱包(wallet)。用户可以在自己的计算机和智能手机上安装钱包应用程序,也可以通过提供钱包服务的网站来使用比特币。
用户通过钱包生成密钥对,并据此在互联网上进行交易。其中,公钥用于接收比特币,而私钥用于支付比特币。私钥保存在钱包中,和一般的密钥对的管理方法一样,不能泄露给别人。
15.3.5 区块链
那么,比特币的交易到底是如何进行的呢?要理解这一点,我们需要先讲一讲比特币中最重要的一个概念——区块链(block chain)。
简单来说,区块链就是保存比特币全部交易记录的公共账簿。全世界使用比特币进行的所有交易都被记录在这一本公共账簿中。顾名思义,区块链就是将交易以区块为单位组织起来,并形成如图15-3所示的这样一根链条。

为了让大家理解比特币交易是如何通过区块链来实现的,我们来思考一下“从Alice的地址A向Bob商店的地址B支付1 BTC"这样一个场景。完成这样一次支付,相当于执行下面两个操作。
⚪地址 A 所能够支付的比特币数量减少 1 BTC
⚪地址B所能够支付的比特币数量增加1BTC
也就是说,支付的本质是“将地址A中减少的金额增加到地址B中”。因此,如果我们有一本公共账簿,记录了比特币体系中所有的地址至今为止所有的交易,那么对于任意一个地址,我们都能够计算出当前它所拥有的比特币数量,而区块链正是用于实现这一目的的这本公共账簿。
如果能够理解这一点,大家也就不难理解为什么区块链的构建和维系对于比特币来说如此重要了吧。
15.3.6 区块的添加
比特币的首付款是以交易(transaction )为单位来进行的,若干条交易会被合并为一个区块,并被添加到区块链中。当P2P网络确认区块的添加后,相应的交易也就成立了。
图15-4所示为几个区块连接起来组成区块链的情形。

一个区块是由若干条交易以及一个区块头所组成的,区块头中保存了“上一个区块的区块头的散列值”。以图 15-4 中的区块 2 为例,其中区块头 2 中保存的散列值 H2 就是根据它前面的区块1的区块头1计算出来的。
此外,区块头中还保存着“本区块所有交易的整体散列值”。例如,区块头 2 中的散列值T2 就是根据区块 2 中记录的所有交易数据计算出的散列值。
区块头中还保存着一个名为nonce的任意数值,以及时间戳(图中省略)等信息。
假设区块 2 中记录的某一条交易中的 1 个比特被修改,那么散列值 T2 就需要重新计算,这样一来区块头 2 的内容就会发生变化,因此区块头 3 中的散列值 H3 也需要重新计算。也就是说,一旦对区块链中的数据进行任何改动,都需要重建所改动的区块之后的所有区块的数据。由此可见,区块头中的两个散列值有效增加了篡改区块链数据的难度。
15.3.7交易
下面我们来看一看区块中记录的交易数据是什么样的。所谓交易,就是对“从一个地址向另一个地址转移了多少比特币”这一事件的描述。
例如,假设Alice从Bob商店购买了商品,需要向Bob商店支付1 BTC的货款。
⚪Bob 商店创建公钥密钥对(公钥 B 和私钥 b)
⚪Bob 商店根据公钥 B 生成地址 B,并发送给 Alice
⚪Alice 创建公钥密钥对(公钥 A 和私钥 a)
⚪Alice创建交易:“从地址A向地址B发送1 BTC"。此时, Alice使用私钥a对交易签署数字签名
⚪Alice 将这条交易发送至 P2P 网络,即向全世界广播这条交易
⚪随后, Alice创建的交易与其他一些交易一起被合并为一个区块,并被
⚪添加到区块链中添加的区块被 P2P网络确认后,“从地址 A 向地址 B 发送 1 BTC”的交易就成立了
此时,外界并不知道“A 是 Alice的地址,B 是 Bob 商店的地址”,但是Alice需要向Bob商店付款, Bob 商店也需要从Alice处收款,因此这条交易到底是谁把钱付给谁,至少 Alice和Bob 商店是要知道的。Alice 和 Bob 商店之间的身份确认,需要通过社交网络、电子邮件、网站等比特币系统之外的渠道来进行。
当交易被合并到区块,并被添加到区块链后,地址A能够支付的金额就减少了1 BTC,而地址 B 能够支付的金额则增加了 1 BTC,这与现实世界中的转账操作具有相同的意义。
在创建交易时运用了数字签名技术。比特币中使用的数字签名算法为椭圆曲线 DSA,其中使用的椭圆曲线方程为x^2=y^3+7。
15.3.8挖矿
到这里为止,我们已经了解了一个地址是如何向另一个地址付款的。然而,交易成立的前提是一方必须拥有一定量的比特币。
随着全世界的比特币交易不断增加,区块链也会随之不断增长,这就意味着P2P网络中的“某个人”在负责将新的区块添加到区块链。有趣的是,“将新的区块添加到区块链”这一行为,370第 15章 密码技术与现实社会正好就相当于“创造新的比特币余额”。向区块链中添加区块就好像从金矿中挖出比特币一样,因此称为挖矿(mining),而从事挖矿的人则称为矿工(miner)。
由于区块链是一条单链,因此在某个特定的时间点只能向其中添加一个区块。按照比特币协议的规定,成功将区块添加到区块链的矿工将获得挖矿奖励(reward)以及该区块所有交易的手续费(transaction fee)。2015年,每个区块的挖矿奖励为25 BTC(约75万日元)。
为了防止比特币被伪造,矿工必须证明自己确实完成了规定量的工作,这种证明称为工作量证明(Proof of Work,PoW)。工作量证明是通过散列值来实现的。
要向区块链添加新的区块,矿工需要生成合法的区块头,而且区块头中“前一区块的散列值”的格式是有规定的,它的前面若干个比特必须为 0。例如,图 15-4 的散列值 H2 可能是下面这样的值。
0000000000000000007780B6F7817C431309EDED44F51223352D86A4436023913
区块头中之所以需要一个称为nonce的任意数值,就是为了凑出像上面这样前面若干比特都是 0 的散列值。也就是说,矿工需要不断更换 nonce进行尝试,直到计算出符合要求的散列值为止。
这个过程实际上和暴力破解单向散列函数十分相似。当然,这只是为了证明某个矿工确实投入了大量的计算资源来完成工作,而并不是真的为了去攻击单向散列函数。比特币系统中大约每10分钟会添加一个新的区块,为了保持这样的恒定速率,计算的难度(即所需的0的个数)会不断地被调整。
15.3.9 确认
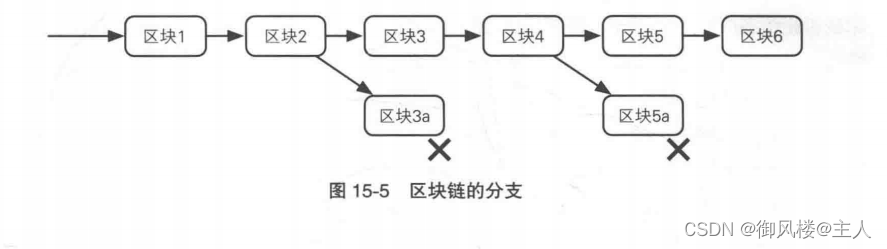
由于全世界有大量的矿工在不断尝试添加新的区块,因此如果在某一个时间点上有多个矿工同时计算出了符合要求的散列值,区块链就有可能会产生分支。由于比特币是一个P2P网络,因此无法确定是哪一个区块先达到的节点,比如节点 1 可能先收到区块A,节点2可能先收到区块B,这样就会造成节点1和节点2的区块链产生差异。到底哪个区块才应该被添加到区块链中呢? P2P网络需要对此做出判断,这个动作称为确认。当产生分支时, P2P网络的各个节点会选择计算量大的分支继续工作,从而抑制区块链继续产生分支。比特币系统假设善意的矿工所拥有的计算资源要大于恶意的矿工所拥有的计算资源,这也是比特币系统得以正常运作的前提。
15.3.10 匿名性
我们可能经常听说“比特币交易是匿名的”,对于这里的“匿名”,我们必须正确理解。诚然,在钱包中生成地址时,我们不需要将这个地址和自己的身份(姓名、邮箱地址)进行关联,也没有必要把自己的身份告诉交易对象。从这个意义上来说,比特币交易的确是匿名的。
然而,看了上面的讲解大家也应该能明白,某个地址所进行的交易会公开给全世界所有用户,而且交易记录也会近似永远地留在区块链上。因此,通常用户不会用同一个地址反复进行交易。
此外,商品交易中本来就需要在一定程度上公开身份信息,不然你也没办法收到商品。换句话说,只要你的交易对象宣布“这个地址就是 Alice的”,那么使用这一地址所进行的交易信息也会随之公开。而且, P2P网络的性质决定了某条交易所对应的节点IP是需要被记录的,这也产生了一定的风险。
举个例子,在Blockchain.info@网站上可以查询区块链的所有数据,就拿我们刚才列举的Jimmy Wales的地址来说,任何人都可以查询与该地址相关的所有交易信息。
将来比特币也许会改进这些匿名性相关的问题。
15.3.11 信任的意义
最后我们来思考一下比特币与信任的问题。比特币不存在管理它的国家和中央银行,那么我们到底能不能信任比特币呢?在这个问题上,我们需要仔细思考“信任”这个词的意义。
下面三个“信任”的意义是各不相同的,请大家注意。
(1)信任使用比特币进行交易的对象。
(2)信任比特币交易所。
(3)信任比特币系统。
“信任使用比特币进行交易的对象”与信任使用现金进行交易的对象是差不多的,这取决于你是否相信在向对方支付比特币之后能够按照约定收到商品。在这一点上,比特币和现金是一样的,当你把现金付给对方之后,如果对方卷钱跑了你也没办法。
“信任比特币交易所”与信任存款的银行是差不多的。
为了减少时间差,同时也为了与其他货币进行兑换,世界上运营着很多比特币交易所。即便比特币系统本身是可信的,交易所还是可能会被盗或者参与欺诈。实际上,2014 年大型交易所 Mt. Gox 就发生了价值数百亿日元的比特币凭空消失的事件。
“信任比特币系统”相当于信任比特币所使用的密码技术以及用于实现这些密码技术的钱包等软件。
比特币系统是基于世界上广泛使用的密码技术以公开的方式设计的,其中并不包含任何隐蔽式安全的要素。从这个意义上来看,比特币系统本身是可信的。
不过,从目前来看,比特币更多地是被看作一种价值剧烈变化的高风险金融产品。尽管出于手续费的优势,比特币很适合用作跨境汇款,但一般认为以比特币的形式保有大量资金的风险还是很高的。
此外,相比比特币系统本身来说,用户还是应该更关注自身的安全管理。
15.3.12 比特币
小结前面我们对比特币进行了一些介绍,现在我们来简单地总结一下。
⚪比特币是一种基于 P2P 网络的支付结算系统,在通过公钥生成的地址之间进行交易
⚪转账的合法性通过发送者用私钥进行数字签名来证明
⚪所有的交易记录都保存在公开账簿(区块链)中,任何人都可以对其中的记录进行验证(透明性)
⚪通过运用单向散列函数使得对区块链的篡改变得非常困难
⚪通过工作量证明防止伪造和区块链产生分支
⚪为了添加新区块,矿工需要计算出前面若干比特为 0 的符合条件的散列值(挖矿)。如果成功添加新区块,矿工将得到一定数量的比特币作为奖励
通过上面的小结我们可以看出,比特币中运用了本书中介绍的各种密码技术。
15.4 追寻完美的密码技术
下面我们来简单介绍一下有望成为“完美的密码技术”的量子密码和量子计算机。它们都是比公钥密码更具冲击性的技术,现在相关研究正在进行之中。
关于量子密码和量子计算的知识,在Singh所著的《密码故事》一书中有通俗易懂的介绍,划此外,以下关于量子密码和量子计算机的内容参考了Singh的《密码故事》以及石井茂的《量子密码》.书中还实际展示了用量子密码进行通信的协议。
15.4.1 量子密码
量子密码是基于量子理论的通信技术,由 Bennett 和 Brassard 于20 世纪 80 年代提出。尽管带有“密码”这个词,但严格来说它并没有直接构成一种密码体系,而是一种让通信本身不可窃听的技术,也可以理解为是一种利用光子的量子特性来实现通信的方法。
最早的量子密码中,利用了下列两个事实。
(1)从原理上说,无法准确测出光子的偏振方向。
根据这一事实,可以让窃听得到的内容变得不正确。
(2)测量行为本身会导致光子的状态发生改变。
根据这一事实,接收者可以判断出通信是否被窃听。
计算机的数据之所以容易被窃听,是因为接收者无法发现窃听这一行为。然而,量子密码通信的情况则不同。如果窃听者 Eve在通信过程中进行了窃听,则一半的数据会变得杂乱,接收者可以据此发觉有人在进行窃听。
请大家回忆一下绝对无法破译的密码——一次性密码本。一次性密码本的最大问题在于难以发送和明文具有相同长度的大量密钥。然而,如果使用量子密码来发送密钥,接收者就可以识别出密钥是否被窃听。也就是说,量子密码让一次性密码本离实用更近了一步。
量子密码有很多种实现方法正在研究之中。BB84 协议用 4 个量子状态代表 1 比特的信息;B92 协议用两个量子状态代表 1 比特的信息;E91 协议和 BB84 协议等价,但它是采用相互纠缠(entangled)的一对光子来实现的。量子纠缠是一种量子现象,只要测定其中一个光子的状态,就可以确定相距很远的另一个光子的状态。
1989年,美国成功实现了32cm距离间的量子密码通信。之后随着研究的发展,2002年日本三菱电机成功实现了当时世界上最长距离的量子密码通信,通信距离为87km。
2007年,NTT研究所的井上恭开发出了差分相移量子密钥配送(DPS-QKD)方法,并成功通过200km的光纤传送了量子密钥。
15.4.2 量子计算机
如果说量子密码是密码学家的终极工具,那么量子计算机就是密码破译者的终极工具。
和量子密码一样,量子计算机也利用了量子理论,由英国物理学家 David Deutsch 于 1985年提出。根据量子理论,粒子可同时具有多种状态。如果使用具有多种状态的粒子进行计算,则可以同时完成多种状态的计算。如果用1 个粒子能够计算0和 1 两种状态,那么用128 个这样的粒子就可以同时计算2^128种状态。换句话说,这就是一台超级并行计算机。
我们知道,只要密钥足够长,密钥空间就会很大,暴力破解需要花费的时间就会变成天文数字。然而,也有人猜想:如果用量子计算机来破译密码,由于可以一次计算多种状态,因此暴力破解岂不是瞬间就可以完成了。当然,到现在为止量子计算机还没有达到实用的程度。
不过, 1994年Peter Shor发表了一种用量子计算机进行快速质因数分解的算法。在随后的2001年, IBM阿尔玛登研究中心( Almaden Research Center )成功实现了将15分解成3 x 5的质因数分解计算。现在,关于量子计算机的研究依然在如火如荼地进行着。
2011 年, D-Wave Systems公司发布了商用量子计算机系统 D-Wave。D-Wave 并不是一台通用计算机,而是为解决最优化问题而设计的专用计算机,在物理上对量子退火(quantumannealing)算法进行了实现。D-Wave可以应用于网络最优化问题、机器学习、图像识别等多个领域,但并不能直接帮助破译密码。
15.4.3 哪一种技术会率先进入实用领域
如果量子密码比量子计算机先进入实用领域,则可以使用量子密码来实现一次性密码本,从而产生完美的密码技术。由于一次性密码本在原理上是无法破译的,因此即便使用量子计算机也无法破译量子密码,因为即便量子计算机能够快速完成暴力破解,也无法判断到底哪一个才是正确的密钥。
然而,如果量子计算机比量子密码先进入实用领域,则使用目前的密码技术所产生的密文将会全部被破译。在量子计算机出现后依然能够抵抗破译的密码称为耐量子密码或者后量子密码(PostQuantum Cryptography, PQCrypto)。其中有一种算法叫作多变量公钥密码(Multivariate PublicKey Cryptosystem),它利用的是 NP 完全问题的复杂度,因此被认为是一种能够对抗量子计算机的密码系统。详情请参见《密码理论与椭圆曲线》一书。
15.5 只有完美的密码,没有完美的人
那么,如果量子密码进入实用领域,我们就能够实现完美的安全吗?很遗憾,这是不可能的。因为在安全问题中,密码技术能够覆盖的范围是非常有限的。在确保系统的整体安全方面,人是一个特别巨大的弱点。
本节中,我们将首先回顾一下目前的密码技术中不完美的部分,并介绍一下“易攻难守”的现状。最后,我们将通过两个攻击的实例,来看一看要防御攻击是多么困难。一个例子是窃听通过PGP加密的电子邮件,另一个则是在使用 SSL/TLS的网站上窃听信用卡号。
15.5.1 理论是完美的,现实是残酷的
密码学家的工具箱看上去已经十八般兵器样样齐全了,有了这些工具,不需要等到量子密码实用化的那一天,我们也可以实现完美的机密性和完美的认证了吧?很遗憾,这只是一个错觉而已。为了配送对称密码的密钥,我们需要使用公钥密码,而为了对公钥进行认证,我们又需要认证机构的公钥。以此类推,无穷无尽,我们必须在某个节点上找到一个公钥是自己能够完全信任的,也就是必须要有一个信任的种子。
当然,通过密码技术,我们可以提高机密性,也能够让认证变得更加容易,但是这并不意味着我们可以实现完美的机密性和完美的认证。
因为有数学依据,因为使用了计算机,我们很容易误认为“这样的技术是完美的”。然而,即便理论上是完美的,在用于现实世界中时也会出现问题。
有人简单地认为,只要使用人的指纹、声纹、面容识别、笔迹识别等生物信息就能够实现完美的认证。然而,采用生物信息的认证技术(生物识别认证, biometric authentication)也并不是完美的认证。
要进行生物识别认证,就必须在某个时间点上将生物信息转换为比特序列,而实际的认证则是通过转换后的比特序列来完成的。因此,如果这些比特序列被窃取,就会和钥匙被偷产生相同的后果。而且,和一般的钥匙不同,生物信息是无法改变的,因为你不可能改变自己的指纹、声音,也不能换一个眼球。
15.5.2 防御必须天衣无缝,攻击只需突破一点
无论如何运用技术都无法实现完美的安全,这个结论听上去很悲观,但其实还有更加悲观的事情,那就是“防御必须天衣无缝,攻击只需突破一点”。
为了保卫系统安全,我们必须应对各种可能发生的攻击,而且这种防御体系必须24小时连续工作。另一方面,要攻击一个系统,则只要找到一种有效的攻击方法,而且只需利用防御方一瞬间的破绽就可以完成了。通过这一事实,大家应该可以想象出相对于防御方,攻击方具有何等巨大的优势。
我们来举一个只需突破一点的例子。假设网上有一个拥有 1000个用户,通过口令进行认证的系统。主动攻击者 Mallory试图伪装成合法的用户来入侵这一系统。在这种情况下,Mallory并不需要对所有1000个用户进行伪装,而是只要伪装成其中一个人就可以了。
Bob就是这 1000 个人中的一个,他是这样想的。
每次登录系统都要输入口令,太长的口令很难记又不方便。反正也没有什么人会破解我的口令入侵我的电脑,再说了,我的电脑里也没有保存什么重要的信息,就算被入侵了也无所谓。所以我还是用个短一点的口令好了。
但是,这样的想法是非常危险的。
Bob 的电脑里可能的确没有什么重要的信息,但是大家不要忘了,Mallory 可以在入侵 Bob的电脑之后,将Bob的电脑当作入侵其他电脑的跳板。
在拥有坚固的密码和认证机制的系统中,即便 1000 个用户里有 999个人的安全意识很高,只要剩下的 1个人没有做好安全管理,那个人就会成为攻击者入侵系统的垫脚石。攻击者只要突破系统中最薄弱的一点就可以了。
15.5.3 攻击实例1:经过PGP加密的电子邮件
密码技术只是信息安全的一部分。为了让大家更好地理解这一观点,我们来看一个对经过密码软件PGP加密的邮件进行攻击的例子。
我们假设 Alice 准备给正在公司上班的 Bob 发送一封邮件,主动攻击者 Mallory 想要读取这封邮件的内容。Alice非常谨慎,她使用PGP对邮件加密后才发送给Bob。那么Mallory该怎么办呢?要破译用PGP加密的邮件,他会不会尝试对RSA中使用的那个很大的数进行质因数分解呢?
Mallory 大概不会这样做,因为比起跟密码技术硬碰硬来说,还有很多其他更有效的攻击方式。
Mallory 可以在 Bob 回家之后入侵 Bob 的电脑并窃取已经解密的邮件,或者还可以趁 Bob不注意,从垃圾桶里找到Bob不经意间打印出来的邮件(Mallory可以穿着清洁公司的服装混入办公室)。此外还可以在 Bob 所使用的公司内部的打印服务器上事先安装恶意程序,这样一来,Bob所打印的内容就会全部通过网络发送给 Mallory。还有更加直接的攻击方式。Mallory可以在 Bob的邮件软件中安装程序,将按下PGP的解密按钮之后显示出来的邮件内容悄悄发送给Mallory。如果直接入侵Bob的电脑很困难,还可以假装成Alice发送下面这样的邮件。
Bob双击这个附件打算玩一下这个游戏,而实际上这个游戏是经过Mallory改造的,在运行的时候会安装另外一个程序。
此外, Mallory还可以收买Bob公司的系统管理员,让他帮忙在Bob的电脑上安装恶意程序。收买一个人总比搞到一台能够破解RSA的超级计算机要便宜多了。
说不定根本不需要收买别人, Mallory自己就可以伪装成系统管理员从Bob嘴里直接套出口买令。这是社会工程学( social engineering )攻击的一种方式。
以此类推,只要愿意,几乎可以想出无数种读取Alice的邮件的方法。而且,这些方法与PGP中使用的密码强度毫无关系。为了防御Mallory的这种无所不在的攻击,需要时刻保持警惕才行。
《应用密码学》一书的作者布鲁斯·施奈尔有一句名言: “信息安全在于流程而非产品”。我们不能因为购买了安全产品就认为可以高枕无忧了,还必须让与系统相关的所有人员时常保持较高的安全意识才行。
15.5.4 攻击实例2:用SSL/TLS加密的信用卡号
下面我们来看一个对使用SSL/TLS的网站进行攻击的例子。
Alice在Bob网上书店购买新书时,都是使用信用卡来支付的。当然, Bob书店的网站是使用 SSL/TLS 进行保护的。
主动攻击者Mallory想要窃取Alice的信用卡号,他要怎样做呢?他会去分析SSL/TLS的握手协议,找出所使用的密码套件,然后去尝试破解 RSA 公钥密码和 Diffie-Hellman 密钥交换吗?不,Mallory才不会这样做。
比如说, Mallory可以入侵Alice的电脑,搜索电脑中的文件,说不定就会找到Alice不经意间保存下来的信用卡号。
就算这样找不着信用卡号, Mallory也不会放弃。他可以在Alice的Web浏览器里植入恶意程序,当 Alice 访问 SSL/TLS 保护的网页时,Web 浏览器就会出错关闭。Alice不知道这个恶意程序的存在,在几次访问 SSL/TLS 网页出错之后,就会感到非常焦急。
Alice:“唉,又出错了,本来还想在午休的时候买本新书的……”
当连续三次出错之后,焦急的 Alice 开始寻找其他方法,她重新看了一下 Bob 书店的网站,发现了这样一个链接。
“无法使用 SSL/TLS 的顾客请点这里”
很多在线购物网站都会准备一个和SSL/TLS网页功能相同的用来下订单的普通网页。
Alice 访问没有通过 SSL/TLS 保护的网页,这次终于正常显示出来了,她松了一口气,输入了信用卡号。这时,在网上监视着这一情况的 Mallory 就轻松地得到了 Alice 的卡号。
实际上,Mallory 甚至用不着在 Alice 的 Web 浏览器上植入程序,也可以监视网络上的数据,并在 Alice 试图访问 Bob 书店的 SSL/TLS 网页时,向 Bob 书店的服务器发送超出其处理能力的大量数据,导致系统瘫痪。当Alice访问没有通过SSL/TLS保护的网页时, Mallory马上停止攻击并进行窃听。
当Web服务器频繁宕机时, Bob书店可能也会发出像“由于系统不稳定,请着急的顾客访问这个网页”这样的通知,引导客户访问没有通过 SSL/TLS 保护的网页。Mallory看到这样的通知真是喜出望外,因为这样他就可以窃听到在Bob书店下订单的顾客的大量信用卡号了。
像上面这样让用户无法使用某种服务的攻击称为拒绝服务攻击(Denial of Service Attack),也称为DoS攻击。拒绝服务攻击是一种针对服务可用性(availability)的攻击方式。拒绝服务攻击并非只是无法使用服务而感到不便这么简单。当安全性高的服务瘫痪时,用户往往会自发地转移到安全性较低的服务。也就是说,通过拒绝服务攻击,可以让窃听等其他攻击更容易进行。
一般来说,拒绝服务攻击是非常简单和原始的。它不需要深奥的数学原理,也不需要高度的密码破译技术,是一种非常简单粗暴的攻击方式,就像把炸弹直接往对方身上扔一样,但它却非常有效。
上面我们展示了对 PGP 和 SSL/TLS 进行攻击的例子,但 Mallory 既没有破解 PGP,也没有破解SSL/TLS。也就是说,在上面的两个例子中,所进行的攻击与密码的强度都是毫无关系的。即便我们不使用PGP和SSL/TLS,而是使用量子密码,这种情况也不会发生丝毫变化。
15.6 本章小结
人类长久以来都在不断改进密码技术,即使到了计算机和互联网时代,这样的技术进步也从未停止。
然而,即便使用计算机,也无法实现完美的密码技术。此外,即便真的有完美的密码技术,也不可能实现完美的安全性。这是因为必然会有人类,即不完美的我们参与其中。
理解了密码技术的意义和局限性之后,我们就要懂得在生活中不应该盲目相信计算机,而是应该注重培养健全的安全意识。
希望本书能够对各位读者在培养安全意识方面有所帮助。
衷心感谢您读完本书。
附录 A 椭圆曲线密码
在附录 1 中我们将为大家介绍一下椭圆曲线密码,不过对于其中的数学知识只能浅尝辄止。如果想更加深入地了解椭圆曲线密码,可以参考《欢迎来到现代密码》①[黑泽馨]、《密码理论与椭圆曲线》[辻井重雄等]、《支撑云计算未来的密码技术》[光成滋生]等著作。此外,关于有限域的计算,在《数学女孩:费马大定理》[结城浩]一书中也进行了介绍。
什么是椭圆曲线密码
椭圆曲线密码( Elliptic Curve Cryptography, ECC)是利用椭圆曲线来实现的密码技术的统称。尽管名字里带有“密码”两个字,但椭圆曲线密码实际上包括以下内容。
⚪基于椭圆曲线的公钥密码
⚪基于椭圆曲线的数字签名
⚪基于椭圆曲线的密钥交换
椭圆曲线密码目前正被广泛使用,例如在SSL/TLS中,就使用了椭圆曲线Diffie-Hellman密钥交换( ECDH、 ECDHE)和椭圆曲线DSA (ECDSA ),虚拟货币比特币(15.3节)中也使用了椭圆曲线 DSA。
椭圆曲线密码可以用比 RSA更短的密钥来实现同等的强度。也就是说,椭圆曲线密码密钥短但强度高。例如,密钥长度为 224~255 比特的椭圆曲线密码,与密钥长度为2048比特的RSA 具备几乎同等的强度。
顺便一提,椭圆曲线(Elliptic Curve,EC)这个名字很容易让人联想到“椭圆形”,但实际上椭圆曲线的图像并不是椭圆形的。而之所以叫椭圆曲线,是有历史原因的,即椭圆曲线源自于求椭圆弧长的椭圆积分的反函数。
一般情况下,椭圆曲线可用下列方程式来表示,其中 a,b,c,d为系数。
![]()
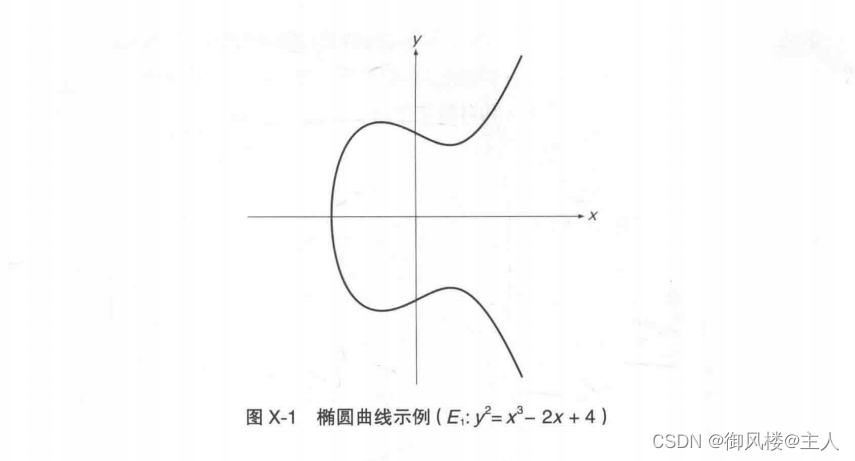
例如,当a=1,b=0,c=-2,d=4时,所得到的椭圆曲线为:
![]()
该椭圆曲线E,的图像如图X-1所示,可以看出根本就不是椭圆形。
椭圆曲线运算
下面我们利用图像来讲解一下椭圆曲线上的“运算”。
首先是加法,请看图 X-2。过曲线上两点 A,B 画一条直线,找到直线与椭圆曲线的交点,我们将该交点关于x轴对称位置的点定义为A+B。可能大家会问:“为什么两个点的加法要这样定义呢?”请大家暂且抛开数字的加法运算概念。在这里,由两个点A,B按上述过程求得的点,就被定义为椭圆曲线上的点A+B。这样的运算称为“椭圆曲线上的加法运算”。
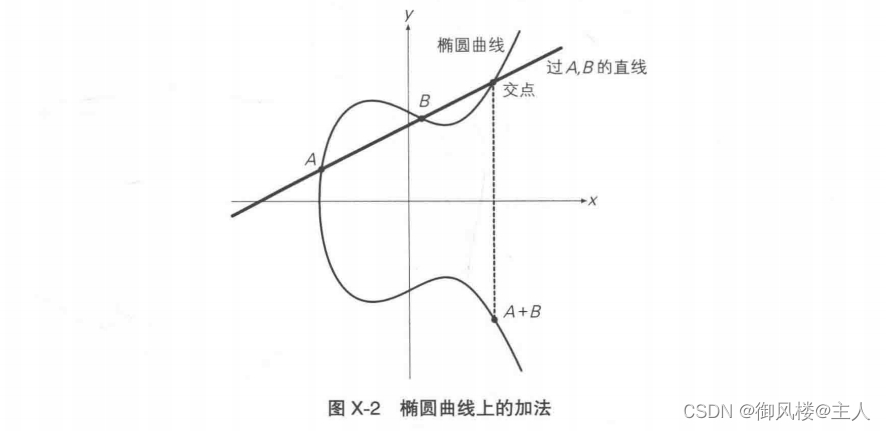
但是,上述定义无法解释 A+A,即两点重合时的情况,因为当两点重合时,无法画出“过两点的直线”。在这种情况下,如图X-3所示,我们画出“曲线在点A 的切线”,然后找到该切线与椭圆曲线的交点,将该交点关于x轴对称位置的点定义为A+A,也就是2A。这样的运算称为“椭圆曲线上的二倍运算”。
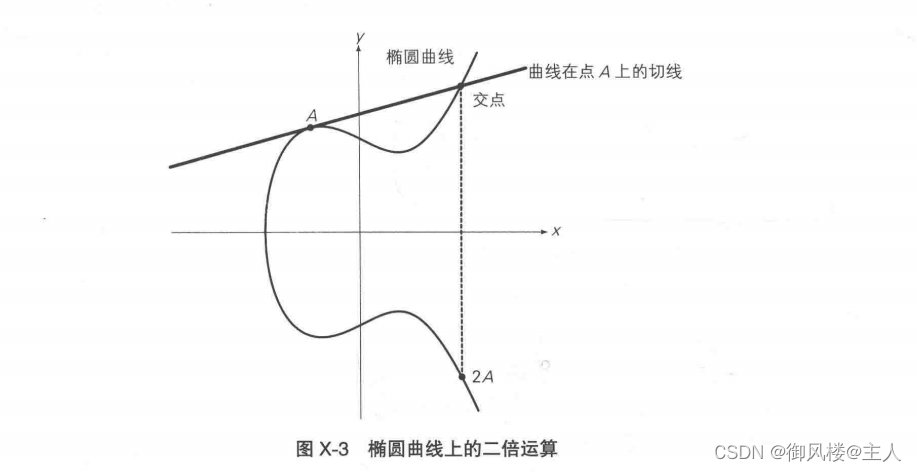
此外,我们将点A关于x轴对称位置的点定义为-A(图 X-4)。这样的运算称为“椭圆曲线上的正负取反运算”。



有限域上的椭圆曲线运算到这里为止,大家对于“椭圆曲线运算”以及“椭圆曲线上的离散对数问题”应该已经有了一个大致的理解,接下来的内容会更复杂一些。其实,椭圆曲线密码所使用的椭圆曲线运算,并不是在上一节中所讲的那种光滑曲线上进行的。
椭圆曲线的图像要形成一条光滑的曲线,其坐标x,y必须都是实数,即“实数域R上的椭圆曲线”。
椭圆曲线密码所使用的椭圆曲线并非在实数域R上,而是在有限域F,上。有限域F,是指对于某个给定的质数p,由0,1......,p-1共p个元素所组成的整数集合中定义的加减乘除运算。有限域中的运算使用的就是我们在5.5节中介绍的时钟运算,大家可以想象一下表盘上有p个数字的时钟,在这个时钟上进行加减乘除运算。更直观一点的话,就是用整数来计算坐标,并将结果除以 p 求余数。
如果大家还是不太清楚“有限域F,上的椭圆曲线”,我们来看一个具体的例子:
E2:y^2=x^3+x+1
当这个椭圆曲线 E, 位于实数域 R 上时,其图像如图 X-5 所示,是一条光滑的曲线。
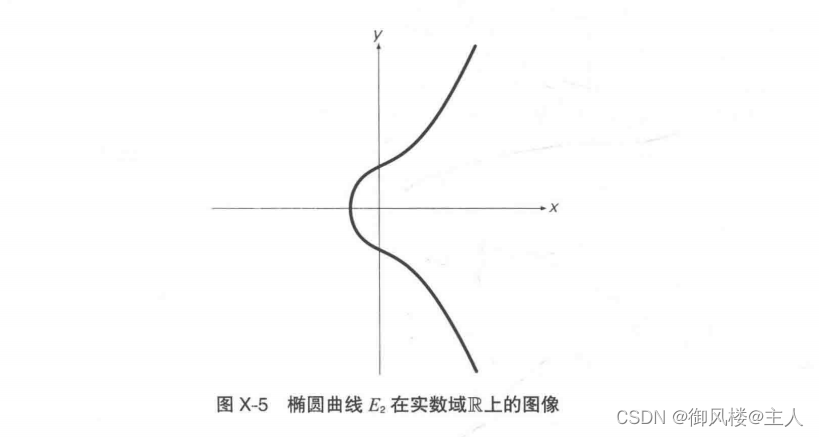



椭圆曲线Diffie-Hellman密钥交换
刚刚我们介绍了“椭圆曲线上的离散对数问题”,接下来我们来看一看具体的密码算法是如何实现的。首先我们来看一看椭圆曲线 Diffie-Hellman 密钥交换。其实除了运用椭圆曲线这一点之外,它的流程与 Diffie-Hellman 密钥交换的流程(11.5 节)基本上是相同的。
非椭圆曲线的 Diffie-Hellman 密钥交换所利用的是:
以p为模,已知G和G^x modp求x的复杂度(有限域上的离散对数问题)
相对地,椭圆曲线 Diffie-Hellman 密钥交换所利用的则是:
⚪在椭圆曲线上,已知 G 和 xG 求 x 的复杂度(椭圆曲线上的离散对数问题)
现在我们假设 Alice 和 Bob 需要共享一个对称密码的密钥,然而双方之间的通信线路已经被窃听者 Eve窃听了。这时, Alice和Bob可以通过以下方法进行椭圆曲线Diffie-Hellman密钥交换,从而生成共享密钥(图X-8)。


椭圆曲线 ElGamal 密码
现在大家已经知道,通过椭圆曲线 Diffie-Hellman 密钥交换, Alice 和 Bob 能够生成共享密钥abG。利用共享密钥abG,我们就可以很容易地实现椭圆曲线ElGamal密码。
假设Alice要向Bob发送一条消息, Alice可以将自己要发送的消息用椭圆曲线上的一个点M来表示(实际上使用的是该点的 x坐标)。
加密
(1) Alice 用自己的私钥 a 以及 Bob 的公钥 bG,对消息 M计算点 M+ abG。此点 M + abG就是密文。
(2) Alice将密文M+abG发送给Bob。
解密
(3) Bob接收到密文M+abG。
(4) Bob 用Alice 的公钥 aG 以及自己的私钥b计算出共享密钥 abG。
(5) Bob 将收到的密文M+ abG减去共享密钥abG得到消息M。
由于窃听者 Eve 无法计算出 abG,因此即便窃取到密文 M+ abG,也无法计算出消息 M。









------------------------------------------
感谢您阅读本文!如果您对文章内容有任何疑问或者想要提出任何问题,欢迎在评论区留言。我会尽力回答您的疑问,并与您交流。期待与您互动。
本书分享完毕,在本章中提及到的比特币我会基于其他书籍来分享,而且不仅限于比特币,会涉及到隐私计算、区块链、以太坊等。


