- 1基于Python的博弈树搜索人机交互五子棋人工智能实验_python五子棋ai
- 2eeglab教程系列(4)-绘制通道光谱图
- 3怎样让你的SQL使用最佳索引!_sql执行器 最优索引是什么
- 4如何在 Windows 上本地免费安装和运行 Llama2_llama2如何windows安装
- 5AndroidStudio案例——图书列表_androidstudio文章列表
- 6动态壁纸软件Live Wallpaper HD mac中文版功能特色
- 7使用OpenCV在Qt C++环境中实现车牌号码的识别_qt opencv 识别车牌
- 8LeetCode —— 栈和队列相关的oj题(含循环队列)_oj双端队列
- 9kafka消息消费不到_kafka某个消费者组下的consumer不能消费消息
- 10java学习资源分享
【MATLAB数据处理实用案例详解(19)】——利用神经模糊控制实现对洗衣机的控制_实现洗衣机洗涤时间的模糊控制
赞
踩
一、问题描述
20世纪90年代初期,日本松下公司推出了神经模糊控制全自动洗衣机这种洗衣机能够自动判断衣物质地的软硬程度、衣量多少、脏污程度和性质等,应用神经模糊控制技术,自动生成模糊控制规则和隶属度函数,预设洗衣水位、水流强度和洗涤时间,在整个洗衣过程中实时调整这些参数,达到最佳的洗衣效果。
洗衣机的主要被控参量为洗涤时间和水流强度,而影响这一输出参量的主要因子是被洗
物的浑油程度和浑浊性质,后者可用浑浊度的变化率来描述。在洗涤过程中,油污的浑浊度变化率小,泥污的浑浊度变化率大。因此,浑浊度及其变化率可以作为控制系统的输入参量,而洗涤时间和水流强度可作为控制量,即系统的输出。实际上,洗衣过程中的这类输入和输出之间很难用一定的数学模型进行描述。系统运行过程中具有较大的不确定性,控制过程在很大程度上依赖操作者的经验,这样一来常规控制方法难以奏效,因此引入模糊控制。
二、洗衣机模糊控制
根据上述的模糊控制基本原理,可得出确定洗涤时间的模糊推理框图,其输入量为洗涤水的浑浊度及其变化率,输出量为洗涤时间,如下图。考虑到适当的控制性能需要和简化程序。定义输入量浑浊度的模糊词集为{清、较浊、浊、 很浊},定义浑浊度变化率的模糊词集为{零、小、中、大},定义输出变量洗涤时间的模糊词集为{短、较短、标准、长}。描述输入/输出变量的词集都具有模糊特性,可以用模糊集合表示。因此模糊概念的确定问题就直接转换为求取模糊集合的隶属函数问题。

洗衣机的模糊控制规则可以归纳为16条,如下:
| 洗衣机的模糊控制规则表 | |||||
|---|---|---|---|---|---|
| 洗涤时间 | 浑浊度 | ||||
| 清 | 较浊 | 浊 | 很浊 | ||
| 变化率 | |||||
| 零 | 短 | 较短 | 标准 | 标准 | |
| 很小 | 标准 | 标准 | 标准 | 标准 | |
| 中 | 标准 | 长 | 长 | 长 | |
| 大 | 标准 | 标准 | 长 | 长 | |
模糊控制的过程是这样的:首先洗衣机获取的浑浊度信息由传感器送到信息处理单元,分为浑独度和浑浊度变化率,送入模糊控制器。对于输入的模糊量,需要将其转换成模糊变量,通过单元片机,利用查表法按照模糊推理法则做出决策,结果被认为是模糊变量,经过去模糊化单元处理,再由执行机构去修改洗涤时间,这样就完成了一次模糊控制算法过程。
一般的模糊控制洗衣机将“专家经验”通过模糊控制规则表现出来,运行中通过查表做出控制决策,这比需要操作者设定程序的电脑控制洗衣机前进了一大步。但是,这种洗衣机由于规则表需要占用大量的内存空间,查表反应速度慢,只能够按照已经编入的规则进行控制因此不够理想。而把神经网络和模糊控制相结合,则能够解决这些问题。
洗衣机的神经网络模糊控制是利用离线训练好的网络,通过在线计算即可得到最佳输出。这种控制模式的反应速度快,而且神经网络又具有自学习功能和联想能力,对于未在训练中出现的样本,也可以通过联系记忆的功能,做出控制决策,表现非常灵活。
洗衣机的神经网络模糊控制器的控制系统中含有多个神经模糊环节,下面仅介绍以浑浊
度和浑浊度变化率为输入变量来确定洗涤时间的控制器。神经模糊控制器在输入/输出参量的选择及模糊论域和模糊子集的确定方面,与一般模糊控制器没有什么区别,只是在推理手段上引入了神经网络。令x1~ x7为输入量浑浊度的模糊子集,x8~ x14为输入量浑浊度变化率的模糊子集,y1 ~ y8为输出控制量的模糊子集。由上图可以看出其中有16条控制规则,每条规则都有一对样本,则共有16对样本。例如,当浑浊度为“清”,浑浊度变化率为“零”时,袭击事件应该为“短”,这个样本可以表示为:
x
=
[
1
,
0.6
,
0.1
,
0
,
0
,
0
,
0
,
1.0
,
0.5
,
0
,
0
,
0
,
0
,
0
]
T
,
y
=
[
1.0
,
0.5
,
0
,
0
,
0
,
0
,
0
,
0
]
T
x=[1,0.6,0.1,0,0,0,0,1.0,0.5,0,0,0,0,0]^T,y=[1.0,0.5,0,0,0,0,0,0]^T
x=[1,0.6,0.1,0,0,0,0,1.0,0.5,0,0,0,0,0]T,y=[1.0,0.5,0,0,0,0,0,0]T
下表为每一个输入参量的模糊量:
| 输入参量的模糊量 | ||
|---|---|---|
| 输入参量 | 模糊量 | |
| 浑浊度 | 清 | 1 0.6 0.1 0 0 0 0 |
| 较浊 | 0 0.6 0.6 0 0 0 0 | |
| 浊 | 0 0 0.6 1 0 0 0 | |
| 很浊 | 0 0 0 0 1 0.6 0 | |
| 浑浊度变化率 | 零 | 1 0.5 0 0 0 0 0 |
| 很小 | 0 0.5 1 0.4 0 0 0 | |
| 中 | 0 0 0 0.4 1 0.6 0 | |
| 大 | 0 0 0 0 0 0 0.8 | |
| 洗涤时间 | 短 | 1 0.5 0 0 0 0 0 0 |
| 较短 | 0.4 0.8 1 0.8 0.4 0.2 0 0 | |
| 标准 | 0 0 0 0.2 0.6 1 0.6 0.2 | |
| 长 | 0 0 0 0 0 0.2 0.5 0.8 | |
根据模糊规则,可以得到网络的训练样本P和T,完整的MATLAB代码如下。
三、运行结果
误差曲线如下:
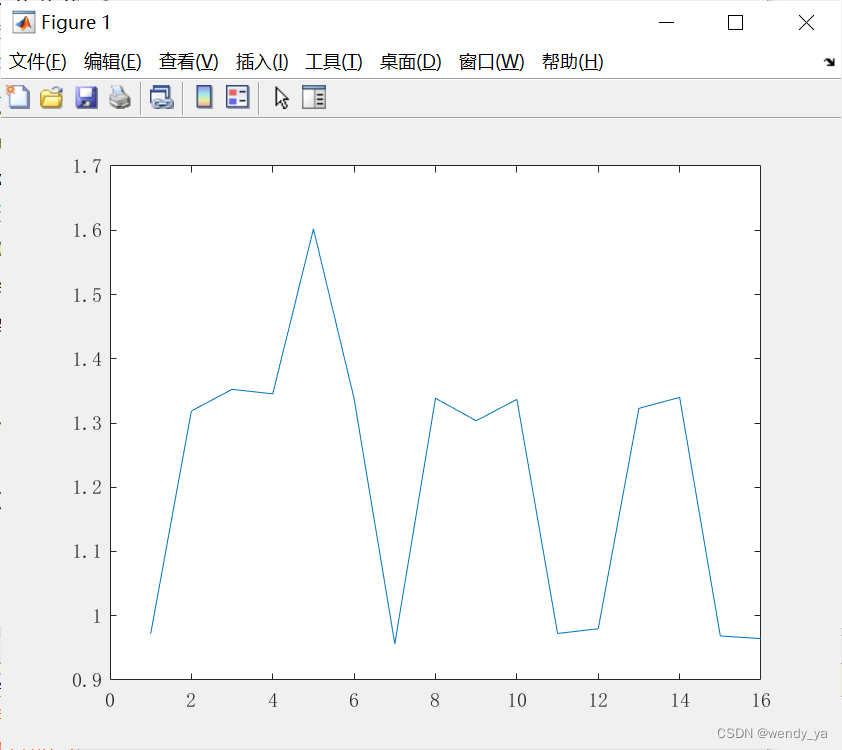
网络经过266次迭代,误差效果满足要求:
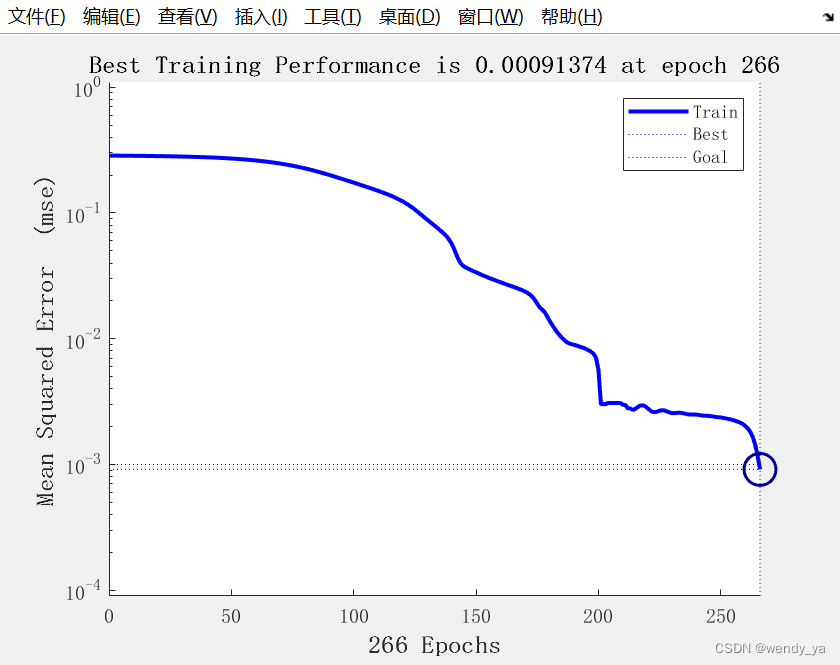
四、完整代码
完整代码可以参考资源:
https://download.csdn.net/download/didi_ya/87740580。
ok,以上便是本文的全部内容了,如果对你有所帮助,记得点个赞哟~


