leetcode分类刷题笔记

写在前面

1、做题如果实在想不出时间复杂度比较优的解法，可以先写出暴力解法，尝试在其基础上优化

2、排序、双指针、二分等–经常可以优化时间复杂度

3、熟悉常用的库，简化代码，提高效率（避免造轮子）

4、简单题先试用暴力解法，不要担心空间和时间复杂度，先拿点case分，再在暴力方法上优化基本都能过

1、内置函数：

https://www.runoob.com/python3/python3-built-in-functions.html

排序：sorted

sorted(iterable, key=None, reverse=False)  
1

key为函数引用：如：int，len，也可以是lambda函数
如：

l = [[2, 2, 3], [1, 4, 5], [5, 4, 9]]
l.sort(lambda x:x[0])  ##按照第一个元素进行排序
print(l)   ##输出：[[1, 4, 5], [2, 2, 3], [5, 4, 9]]
reverse= False：默认从小到大
1
2
3
4

其他字典排序，字符排序例子可见：
https://www.cnblogs.com/dyl01/p/8563550.html

多列排序：

d1 = [{'name':'alice', 'score':38}, {'name':'bob', 'score':18}, {'name':'darl', 'score':28}, {'name':'christ', 'score':28}]
l = sorted(d1, key=lambda x:(-x['score'], x['name']))
print(l)
//输出
//[{'name': 'alice', 'score': 38}, {'name': 'christ', 'score': 28}, {'name': 'darl', 'score': 28}, {'name': 'bob', 'score': 18}]
1
2
3
4
5

重大发现——自定义排序，类似于java中重写比较器

functools包的cmp_to_key使用方法，cmp_to_key接受一个比较器

from functools import cmp_to_key
class Solution:
    def minNumber(self, nums: List[int]) -> str:
        return "".join(sorted([str(i) for i in nums],key=cmp_to_key(lambda x,y:1 if x+y>y+x else -1)))
1
2
3
4

过滤：filter(条件，可迭代对象)

filter(function, iterable)
function返回bool值，可以是lambda表达式

def is_odd(n):
    return n % 2 == 1
 
newlist = filter(is_odd, [1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
print(newlist)

》》[1, 3, 5, 7, 9]
1
2
3
4
5
6
7

返回数据和索引：enumerate()

enumerate(sequence, [start=0])
1

sequence – 一个序列、迭代器或其他支持迭代对象。
start – 下标起始位置。
返回 enumerate(枚举) 对象。

>>>seasons = ['Spring', 'Summer', 'Fall', 'Winter']
>>>list(enumerate(seasons))
[(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
>>>list(enumerate(seasons, start=1))       # 小标从 1 开始
[(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]
1
2
3
4
5

表达式求值： eval()

eval(expression[, globals[, locals]])
1

expression – 表达式。
globals – 变量作用域，全局命名空间，如果被提供，则必须是一个字典对象。
locals – 变量作用域，局部命名空间，如果被提供，可以是任何映射对象。

>>>x = 7
>>> eval( '3 * x' )
21
>>> eval('pow(2,2)')
4
>>> eval('2 + 2')
4
>>> n=81
>>> eval("n + 4")
85
1
2
3
4
5
6
7
8
9
10

进制转换 bin(x),hex(x),oct(x)

x – 整数。
返回2,16,8进制字符串。

ASCII、字符转换chr()，ord()
chr(ASCII)–把ASCII码转换为字符
ord(char)–把字符转换为ASCII码

集合，set（）

即去重后的字典{}，可以执行交并差的集合运算，在表达式求值中可能用到

//定义
set([iterable])

//使用
>>>x = set('runoob')
>>> y = set('google')
>>> x, y
(set(['b', 'r', 'u', 'o', 'n']), set(['e', 'o', 'g', 'l']))   # 重复的被删除
>>> x & y         # 交集
set(['o'])
>>> x | y         # 并集
set(['b', 'e', 'g', 'l', 'o', 'n', 'r', 'u'])
>>> x - y         # 差集
set(['r', 'b', 'u', 'n'])

//常用
set().add()---------自动去重
set ().remove()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2、内置库：

详细可见：
https://www.cnblogs.com/traditional/p/10444299.html

0、math库

常数：e，pi，tau
三角函数：
反三角函数：
对数：
指数：
幂函数：pow(x,y)=x**y
最大公约数：gcd(a,b)
阶乘：factorial(n)
二范数：hypot(x,y)

1、collections：容器数据类型

a）Counter： 计数器，用于统计元素的数量，返回字典，在统计字符串中字母出现个数时非常方便
b）OrderDict：有序字典
c）defaultdict(参数)：值带有默认类型的字典，默认类型为参数类型（如：list，int，None等），缺少的键使用get()返回一个该类型的缺省值

注：普通字典类，使用get(键，默认值)：没有该键就返回缺省值

d）namedtuple：可命名元组，通过名字来访问元组元素
e）deque :双向队列，队列头尾都可以放，也都可以取（与单向队列对比，单向队列只能一头放，另一头取）

2、heapq：堆排序算法

heappush(heap,item) 往堆中插入一条新的值
heappop(heap) 从堆中弹出最小值
heapreplace(heap,item) 从堆中弹出最小值，并往堆中插入item
heappushpop(heap,item) Python3中的heappushpop更高级
heapify(x) 以线性时间将一个列表转化为堆
merge(*iterables,key=None,reverse=False) 合并对个堆，然后输出
nlargest(n,iterable,key=None) 返回可枚举对象中的n个最大值并返回一个结果集list
nsmallest(n,iterable,key=None) 返回可枚举对象中的n个最小值并返回一个结果集list

3、copy：遇到二维数组最好 不要直接赋值（赋值还是引用）

浅拷贝
a2 = copy.copy(a)
深拷贝
a2 = copy.deepcopy(a)

4、itertools：迭代器工具

count()
生成无界限序列，count(start=0, step=1) ，示例从100开始，步长为2，循环10，打印对应值；必须手动break，count()会一直循环。

product(iter1,iter2, … iterN, [repeat=1]);
创建一个迭代器，生成表示item1，item2等中的项目的笛卡尔积的元组，repeat是一个关键字参数，指定重复生成序列的次数

permutations() ：全排列

5、queue:队列

普通队列 和 栈 直接可以用list模拟就好了，使用pop和append就好，可以完成
栈：
尾部FIFO：.pop() .append()
队列：
尾进头出：append() pop(0)
头进尾出：insert(0,obj) pop()

使用queue的PriorityQueue模块可以实现优先队列：

按照优先级出队列和入队列，默认优先级数字越小越高，当没有传递优先级时，采用数字本身大小的排序号作为优先级，越小的数字优先级越低。

PriorityQueue提供的方法：
put:入queue
get:出queue
empty():判空

from queue import PriorityQueue
class Solution:
    def connectSticks(self, sticks: list) -> int:
        cost=0
        q=PriorityQueue()
        for i in sticks:
            q.put(i)
        while not q.empty():
            a=q.get()
            if  q.empty():
                return cost
            else:
                b=q.get()
                q.put(a+b)
                cost+=a+b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

1、二分查找

总结：
适用题型：
index查找或数值查找,不一定需要有序，重点是选择区间的条件需要根据题目意思来构造
代码模板：
1、初始化左右指针
2、循环终止条件：while left <= right或while left < right:
3、迭代：mid = left + (right - left) // 2
4、判定条件，选择下一个搜索区间：修改左右指针：
left = mid + 1，防止整除使得right-left为1时，left不变，进入死循环
right = mid-1，防止left与left相等，但是mid不满足return条件，进入死循环
5、循环终止返回值：left，与right需要根据题意不同，返回不同

leetcode35：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
输入: [1,3,5,6], 5
输出: 2

    class Solution:
        def searchInsert(self, nums: List[int], target: int) -> int:
            left = 0
            right = len(nums) - 1
            while left <= right:
                mid = left + (right - left) // 2 
                if nums[mid] == target:return mid
                elif nums[mid] < target:
                    left = mid + 1
                else:
                    right = mid-1
            return left
1
2
3
4
5
6
7
8
9
10
11
12

leetcode69:

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。
示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。

     class Solution:
        def mySqrt(self, x: int) -> int:
            if x==0 or x==1:
                return x
            low=0
            up=x
	        while (up>=low):
	            mid = (low + up) // 2
	            if mid>x/mid:
	                up=mid-1
	            elif mid<x/mid:
	                low=mid+1
	            else:
	                return mid
        	return up
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

注：此处采用除法判断，因此需要处理0,1特殊值
也可采用乘法判断

    class Solution:
        def mySqrt(self, x: int) -> int:
            low=0
            up=x
            while (up>=low):
                mid = (low + up) // 2
                if mid*mid>x:
                    up=mid-1
                elif mid*mid<x:
                    low=mid+1
                else:
                    return mid
            return up
1
2
3
4
5
6
7
8
9
10
11
12
13

leetcode167：

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

这个题由于是找出两个值，所以感觉二分不太好用，大多数采用的双指针

leetcode278:

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例:

给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。

    class Solution:
        def firstBadVersion(self, n):
            """
            :type n: int
            :rtype: int
            """
            left=1
            right=n
            while left<=right:
                mid=(left+right)>>1
                if isBadVersion(mid):
                    if not isBadVersion(mid-1):
                        return mid
                    right=mid-1
                else:
                    left=mid+1
            return left
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

二分查找进阶（中等）

leetcode33：搜索旋转排序数组

分段有序
假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4
示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

    class Solution:
        def search(self, nums: List[int], target: int) -> int:
            n = len(nums)
            if n == 0:
                return -1
            left = 0
            right = n - 1
            while left < right:
                mid = left + (right - left) // 2
                if nums[mid] == target:
                    return mid
                elif nums[left] <= nums[mid]:
                    if nums[left] <= target < nums[mid]:
                        right = mid - 1
                    else:
                        left = mid + 1
                else:
                    if nums[mid] < target <= nums[right]:
                        left = mid + 1
                    else:
                        right = mid - 1
            #print(left,right)
            return left if nums[left] == target else -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

注意：
1、循环条件不包含等于=
2、程序结束输出前判断
说明：
在二分查找的判断中嵌套了一层判断，用于判断mid分割的区间，那一个为有序区间，若为有序区间，则判断target是否在该区间内

leetcode34：在排序数组中查找元素的第一个和最后一个位置

有重复数字

    class Solution:
        def searchRange(self, nums: list, target: int):
            idx=[-1,-1]
            if not nums:
                return idx
            left,right=0,len(nums)-1
            while left<=right:
                mid=(left+right)>>1
                if nums[mid]==target:
                    idx[0]=mid
                    while idx[0]>0 and nums[idx[0]-1]==target:
                        idx[0]-=1
                    idx[1]=mid
                    while idx[1]<len(nums)-1 and nums[idx[1]+1]==target:
                        idx[1]+=1
                    return idx
                elif nums[mid]<target:
                    left=mid+1
                else:
                    right=mid-1
            return idx
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

思路是二分找到mid，依次向两边拓展找到第一个和最后一个

leetcode162：寻找峰值

数组没有绝对的大小关系，但是可以根据mid处的斜率（mid与mid-1和mid+1的大小关系，判断下一个区间为左右哪个区间）
峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

示例 1:

输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素，你的函数应该返回其索引 2。

    class Solution:
        def findPeakElement(self, nums: List[int]) -> int:
    
            left,right=0,len(nums)-1
            while left<right:
                mid=(left+right)>>1
                if nums[mid]<nums[mid+1]:
                    left=mid+1
                elif nums[mid-1]>nums[mid]:
                    right=mid-1
                else:
                    return mid
            return left
1
2
3
4
5
6
7
8
9
10
11
12
13

2、二叉树遍历

（1）BFS：

基本实现

一、队列实现

1、初始化队列，加入根节点
2、while 循环条件：队列不为空：
执行：
（做你需要做的任务：如打印当前值，记录层数等），从队列取出节点，如果该节点左孩子不为空，则加入队列，如果右孩子不为空，则继续加入队列。
https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        ans=[]
        q=[root]
        while q:
            ceng=[]#这一层的数值
            qtmp=[]#下一层的节点
            for i in range(len(q)):
                node=q.pop(0)
                ceng.append(node.val)
                if node.left:
                    qtmp.append(node.left)
                if node.right:
                    qtmp.append(node.right)
            q=qtmp
            ans.append(ceng)
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

二、递归实现

最简单的解法就是递归，首先确认树非空，然后调用递归函数 helper(node, level)，参数是当前节点和节点的层次。程序过程如下：
1、输出列表称为 levels，当前最高层数就是列表的长度 len(levels)。比较访问节点所在的层次 level 和当前最高层次 len(levels) 的大小，如果前者更大就向 levels 添加一个空列表。
2、将当前节点插入到对应层的列表 levels[level] 中。
3、递归非空的孩子节点：helper(node.left / node.right, level + 1)
样例程序：
https://leetcode-cn.com/problems/binary-tree-level-order-traversal/

class Solution:
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        levels = []
        if not root:
            return levels
        
        def helper(node, level):
            # start the current level
            if len(levels) == level:
                levels.append([])

            # append the current node value
            levels[level].append(node.val)

            # process child nodes for the next level
            if node.left:
                helper(node.left, level + 1)
            if node.right:
                helper(node.right, level + 1)
            
        helper(root, 0)
        return levels
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

leetcode100：相同的树

给定两个二叉树，编写一个函数来检验它们是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

全部都对比完，没有提前返回，则为True

    class Solution1:
        def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
            #         使用队列
            pl, ql = [p], [q]
            while pl and ql:
                a = pl.pop(0)
                b = ql.pop(0)
    
                if a == None and b == None:
                    continue
                if a == None or b == None or a.val != b.val:
                    return False
    
                pl.append(a.left)
                ql.append(b.left)
                pl.append(a.right)
                ql.append(b.right)
            return True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

也可采用递归，依次判断当前值和左右子树是否相同

    #递归判断方法，写起来简单
    class Solution:
        def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
            if not p and not q:
                return True
            if not p or not q:
                return False
            return p.val==q.val and self.isSameTree(p.left,q.left) \
                   and self.isSameTree(p.right, q.right)
1
2
3
4
5
6
7
8
9

leetcode101：对称二叉树

    class Solution:
        def isSymmetric(self, root: TreeNode) -> bool:
            p=[root]
            q=[root]
            while q and p:
                r1=p.pop(0)
                r2=q.pop(0)
                if not r1 and not r2:
                    continue
                if not r1 or not r2 or r1.val!=r2.val:
                    return False
                p.append(r1.left)
                p.append(r1.right)
                q.append(r2.right)
                q.append(r2.left)
            return True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

采用递归：

    #创建镜像子函数，递归调用该函数
    class Solution:
        def isSymmetric(self, root: TreeNode) -> bool:
            return self.ismirror(root, root)
    
        def ismirror(self, r1, r2):
            if not r1 and not r2:
                return True
            if not r1 or not r2:
                return False
            return r1.val == r2.val and \
                   self.ismirror(r1.right, r2.left) and self.ismirror(r2.right, r1.left)
1
2
3
4
5
6
7
8
9
10
11
12

leetcode107：二叉树的层次遍历 II

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

    class Solution:
        def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
            if not root:
                return []
                    
            ceng_all=[]
            p=[root]
            while p:
                l=len(p)
                ceng=[]
                for i in range(l):
    
                    if p[0].val!=None:
                        ceng.append(p[0].val)
                    if p[0].left:
                        p.append(p[0].left)
                    if p[0].right:
                        p.append(p[0].right)
                    
                    p.pop(0)
                ceng_all.append(ceng)
            return ceng_all[::-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

该广度优先遍历，while中嵌套for循环，记录每层的信息，还可用于计算树的深度
（最大深度：while循环，处理一层深度加一，while循环结束即可；
最小深度，处理到叶子节点即可返回深度）

leetcode周赛150：地图分析

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。
示例 1：

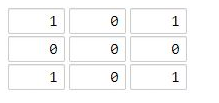
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

解题思路：
采用四叉树的数据结构；把地图上每块陆地作为初始根节点，像前后左右四个方向进行广度优先遍历（考虑边界条件），遍历到的海洋置为陆地，并将距离数据存入队列当中，这样最后到达的一块海洋则是我们要找的海洋（所有海洋中距离陆地最远）：

class Solution:
    def maxDistance(self, grid: list) -> int:
        r, c = len(grid), len(grid[0])
        rot = list()
        for i in range(r):
            for j in range(c):
                if grid[i][j] == 1:
                    rot.append((i, j, 0))

        d = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        res = 0
        while rot:
            i, j, res = rot.pop(0)
            for xd, yd in d:
                x = i + xd
                y = j + yd
                if 0 <= x < r and 0 <= y < c and grid[x][y] == 0:
                    grid[x][y] = 1
                    rot.append((x, y, res + 1))

        return res if res != 0 else -1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

leetcode1298. 你能从盒子里获得的最大糖果数

给你 n 个盒子，每个盒子的格式为 [status, candies, keys, containedBoxes] ，其中：

状态字 status[i]：整数，如果 box[i] 是开的，那么是 1 ，否则是 0 。
糖果数 candies[i]: 整数，表示 box[i] 中糖果的数目。
钥匙 keys[i]：数组，表示你打开 box[i] 后，可以得到一些盒子的钥匙，每个元素分别为该钥匙对应盒子的下标。
内含的盒子 containedBoxes[i]：整数，表示放在 box[i] 里的盒子所对应的下标。
给你一个 initialBoxes 数组，表示你现在得到的盒子，你可以获得里面的糖果，也可以用盒子里的钥匙打开新的盒子，还可以继续探索从这个盒子里找到的其他盒子。

请你按照上述规则，返回可以获得糖果的 最大数目 。
示例 1：
输入：status = [1,0,1,0], candies = [7,5,4,100], keys = [[],[],[1],[]], containedBoxes = [[1,2],[3],[],[]], initialBoxes = [0]
输出：16
解释：
一开始你有盒子 0 。你将获得它里面的 7 个糖果和盒子 1 和 2。
盒子 1 目前状态是关闭的，而且你还没有对应它的钥匙。所以你将会打开盒子 2 ，并得到里面的 4 个糖果和盒子 1 的钥匙。
在盒子 1 中，你会获得 5 个糖果和盒子 3 ，但是你没法获得盒子 3 的钥匙所以盒子 3 会保持关闭状态。
你总共可以获得的糖果数目 = 7 + 4 + 5 = 16 个。
https://leetcode-cn.com/problems/maximum-candies-you-can-get-from-boxes/

思路: 队列实现BFS
对于第 i 个盒子，我们只有拥有这个盒子（在初始时就拥有或从某个盒子中开出）并且能打开它（在初始时就是打开的状态或得到它的钥匙），才能获得其中的糖果。我们用数组 has_box 表示每个盒子是否被拥有，数组 can_open 表示每个盒子是否能被打开。在搜索前，我们只拥有数组 initialBoxes 中的那些盒子，并且能打开数组 status 值为 0 对应的那些盒子。如果一个盒子在搜索前满足这两条要求，就将其放入队列中。

在进行广度优先搜索时，每一轮我们取出队首的盒子 k 将其打开，得到其中的糖果、盒子 containedBoxes[k] 以及钥匙 keys[k]。我们将糖果加入答案，并依次枚举每个盒子以及每把钥匙。在枚举盒子时，如果该盒子可以被打开，就将其加入队尾；同理，在枚举钥匙时，如果其对应的盒子已经被拥有，就将该盒子加入队尾。当队列为空时，搜索结束，我们就得到了得到糖果的最大数目。

class Solution:
    def maxCandies(self, status: List[int], candies: List[int], keys: List[List[int]], containedBoxes: List[List[int]], initialBoxes: List[int]) -> int:
        n = len(status)
        can_open = [status[i] == 1 for i in range(n)]
        has_box, used = [False] * n, [False] * n
        
        q = collections.deque()
        ans = 0
        for box in initialBoxes:
            has_box[box] = True
            if can_open[box]:
                q.append(box)
                used[box] = True
                ans += candies[box]
        
        while len(q) > 0:
            big_box = q.popleft()
            # 遍历盒子中的钥匙，更新q
            for key in keys[big_box]:
                can_open[key] = True
                if not used[key] and has_box[key]:
                    q.append(key)
                    used[key] = True
                    ans += candies[key]
            # 遍历盒子中的盒子，更新q
            for box in containedBoxes[big_box]:
                has_box[box] = True
                if not used[box] and can_open[box]:
                    q.append(box)
                    used[box] = True
                    ans += candies[box]
        
        return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

（2）DFS：

基本思想和实现

深度优先遍历包含：先序、中序、后序遍历；其中的先中后值得是根节点，左右孩子的先后顺序都是左孩子–》右孩子

图解

• 1 先序遍历
  
• 2 中序遍历
  
• 3 后序遍历
  

一个重要的知识点是，根据中序，和先序（后序），写出后序（先序）

知道先序是根->左->右，中序是左->根->右，后序是左->右->根；
最重要的一点就是：（根据先序或后序）找到根（根在先序第一个，后序最后一个）->（根据根在中序）找到左右子树；一直重复这个操作，直到最后一个子节点。

递归实现

先序：

    def preorder(self, root):
          """递归实现先序遍历"""
          if root == None:
              return
          print root.elem
          self.preorder(root.lchild)
          self.preorder(root.rchild)
1
2
3
4
5
6
7

中序：

    def inorder(self, root):
          """递归实现中序遍历"""
          if root == None:
              return
          self.inorder(root.lchild)
          print root.elem
          self.inorder(root.rchild)
1
2
3
4
5
6
7

后序：

    def postorder(self, root):
          """递归实现后续遍历"""
          if root == None:
              return
          self.postorder(root.lchild)
          self.postorder(root.rchild)
          print root.elem
1
2
3
4
5
6
7

堆栈实现

    def preorder(self, root):
        stack=[root]
        """栈实现先序遍历"""
        while stack:
            cur=stack.pop()
            print(cur.val)
            if cur.left:
                stack.append(cur.left)
            if cur.right:
                stack.append(cur.right)
1
2
3
4
5
6
7
8
9
10

leetcode112：二叉树路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

    class Solution:
        def hasPathSum(self, root: TreeNode, sum: int) -> bool:
            if not root:
                return False
            q = [(root.val, root)]
            allsum = []
            while q:
                cursum, node = q.pop()
    
                if not node.right and not node.left:
                    allsum.append(cursum)
                if node.left:
                    q.append((cursum + node.left.val, node.left))
                if node.right:
                    q.append((cursum + node.right.val, node.right))
            return sum in allsum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

深度优先搜索没有层数信息，一般可以将层数和其他信息，与节点一起加入栈中。
也可使用递归：

    class Solution:
        def hasPathSum(self, root: TreeNode, sum: int) -> bool:
            if not root:
                return False
            if not root.left and not root.right:
                return sum==root.val
            else:
                return self.hasPathSum(root.right,sum-root.val) or \
                       self.hasPathSum(root.left,sum-root.val)
1
2
3
4
5
6
7
8
9

leetcode230：二叉搜索树中第K小的元素

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

    class Solution:
        def kthSmallest(self, root: TreeNode, k: int) -> int:
            global num,ans
            num=0
            ans=None
            
            def dfs(root,k):
                global num,ans
                if not root:
                    return None
                dfs(root.left,k)
                num+=1
                if num==k:
                    ans=root.val
                    return None
                dfs(root.right,k)
            dfs(root,k)
            return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

中序遍历的顺序，可将BST按大小遍历

二叉树理解

leetcode周赛143:二叉树寻路

https://leetcode-cn.com/contest/weekly-contest-143/problems/path-in-zigzag-labelled-binary-tree/

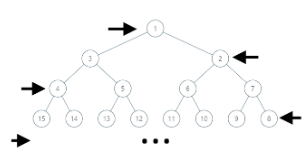
二叉树按照层次遍历，赋给下标，给定某个节点下标，可以根据下标计算其父亲节点的下标

输入：label = 14
输出：[1,3,4,14]

class Solution:
    def dfs(self,lev,x:int):
        if lev==1:
            return [1]
        rtn=self.dfs(lev-1,x//2)
        node=(1<<(lev-1));real=x
        if lev&1:
            # 实际下标=当前层数可容纳的最多的数字-当前层的个数
            real=node*2-(x-node)-1
        rtn.append(real)
        return rtn
    def pathInZigZagTree(self, label: int):
        lev=0;now=label
        while now>0:
            now//=2
            lev+=1
        node=(1<<(lev-1));real=label
        if lev&1:#奇偶判断
            real=(node*2-label)+node-1
        return self.dfs(lev,real)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3、二叉树搜索树BST操作

4、图遍历算法

（1）leetcode200. 岛屿数量（连通域个数）

可拓展4连通为8连通

给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 2:

输入:
11000
11000
00100
00011
采用DFS，

    class Solution1:
        def numIslands(self, grid: list) -> int:
            try:
                m = len(grid)
                n = len(grid[0])
            except:
                return 0
    
            # -------------------------DFS 开始------------------------
            # 定义dfs递归方程
            def dfs(i, j):
                if 0 <= i < m and 0 <= j < n and int(grid[i][j]):
                    grid[i][j] = '0'
                    for a, b in ((1, 0), (0, -1), (-1, 0), (0, 1)):
                        dfs(i + a, j + b)
    
            # ---------------------------------------------------------
    
            r = 0
            for i in range(m):
                for j in range(n):
                    r += int(grid[i][j])
                    dfs(i, j)  # 调用dfs沉没一整块陆地
            return r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

8连通修改一下元组即可

（1）leetcode5257. 统计封闭岛屿的数目

有一个二维矩阵 grid ，每个位置要么是陆地（记号为 0 ）要么是水域（记号为 1 ）。

我们从一块陆地出发，每次可以往上下左右 4 个方向相邻区域走，能走到的所有陆地区域，我们将其称为一座「岛屿」。

如果一座岛屿 完全 由水域包围，即陆地边缘上下左右所有相邻区域都是水域，那么我们将其称为 「封闭岛屿」。

请返回封闭岛屿的数目。

输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

在上一题的基础上判断岛屿有没有与边界接壤
简单暴力的办法可以先dfs边缘的数据；我是采用类变量flag在dfs过程中判断

class Solution:
    def __init__(self):
#         类里面的全局变量失效，应该采用这个形式传递参数
        self.flag=0
    def closedIsland(self, grid) -> int:
        try:
            m = len(grid)
            n = len(grid[0])
        except:
            return 0

        # -------------------------DFS 开始------------------------
        # 定义dfs递归方程
        def dfs(i, j):

            if 0 <= i < m and 0 <= j < n and not grid[i][j]:
#                     如果是碰到边缘的陆地，则不是我们想要的岛屿
                if (i == 0 or i == m - 1 or j == 0 or j == n - 1):
                    self.flag = 0

                grid[i][j] = 1
                for a, b in ((1, 0), (0, -1), (-1, 0), (0, 1)):
                    dfs(i + a, j + b)

        # ---------------------------------------------------------

        r = 0
        for i in range(m):
            for j in range(n):
                self.flag  = 1 - grid[i][j]  # 当前是一块陆地则   flag=1
                dfs(i, j)  # 调用dfs沉没一整块陆地
                r += self.flag
        return r
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

（2）leetcode周赛140. 活字印刷（全排列去重）

你有一套活字字模 tiles，其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。
输入：“AAB”
输出：8
解释：可能的序列为 “A”, “B”, “AA”, “AB”, “BA”, “AAB”, “ABA”, “BAA”。

示例 2：

输入：“AAABBC”
输出：188

提示：
1 <= tiles.length <= 7
tiles 由大写英文字母组成

采用递归实现DFS，完成全排列，使用set去重
核心部分：回溯的时候，将后继节点的状态修改为可发现（这一点和一般的图DFS不同）

class Solution(object):
    def numTilePossibilities(self, tiles):
        """
        :type tiles: str
        :rtype: int
        """
        ans = set()
        v=[True]*len(tiles)
        now = []
        def dfs(x):
            if x >= len(tiles):
                return
            for i in range(len(tiles)):
                if v[i]:
                    v[i] = False
                    now.append(tiles[i])
                    ans.add(''.join(now))
                    dfs(x+1)
                    # 发现完该节点的最深的树后，将该节点置为可见，以备下次发现
                    # now用于存储当前发现的子树的所有信息
                    v[i] = True
                    now.pop()
        dfs(0)
        return len(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

（3）leetcode5309. 连通网络的操作次数

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-operations-to-make-network-connected
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解法1： 并查集
并查集原理详见：https://www.cnblogs.com/yscl/p/10185293.html
主要包含：初始化方式，查的递归实现和迭代实现（路径压缩），并

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        uf = [-1 for i in range(n + 1)]
        global sets_count
        sets_count = n
# 查
        def find(p):
            while uf[p] >= 0:
                p = uf[p]
            return p
# 并
        def union(p, q):
            global sets_count
            proot = find(p)
            qroot = find(q)
            if proot == qroot:
                return
            elif  uf[proot] >  uf[qroot]:   # 负数比较, 左边规模更小
                 uf[qroot] +=  uf[proot]
                 uf[proot] = qroot
            else:
                 uf[proot] +=  uf[qroot]  # 规模相加
                 uf[qroot] = proot
            sets_count -= 1                    # 连通后集合总数减一
        if n-1 >len(connections):
            return -1

        for a,b in connections:
            union(a,b)
        return sets_count-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

一个简版：

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        D = list(range(n))
        def T(a):
            if D[D[a]] == D[a]:
                return D[a]
            D[a] = T(D[a])
            return D[a]
        def C(a, b):
            if T(a) != T(b):
                D[T(a)] = T(b)
                return 1
            return 0
        if len(connections) < n - 1:
            return -1
        return n - 1 - sum(C(a, b) for a, b in connections) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

解法2：图遍历
参考https://leetcode-cn.com/problems/number-of-operations-to-make-network-connected/submissions/

from collections import deque
class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        num_component = 0  #G中连通分量的数目
        num_remains = 0    #G中冗余边的数目
        
        #构建图G的邻接表表示：
        G = []
        for i in range(0, n):
            G.append([])
        for pair in connections:
            G[pair[0]].append(pair[1])
            G[pair[1]].append(pair[0])
        
        #以BFS统计G中连通分量和冗余边的数目：
        color = [0] * n
        for computer in range(0, n):
            if(color[computer] != 0):
                continue
            #对新发现的包含computer的连通分量进行遍历
            num_component += 1
            num_node = 0    #该连通分量中的结点数
            num_degree = 0  #该连通分量中所有结点度的和
            Q = deque([])
            Q.append(computer)
            color[computer] = 1
            while(len(Q) != 0):
                u = Q.popleft()
                num_node += 1
                for v in G[u]:
                    if not color[v]:
                        color[v] = 1
                        Q.append(v)
                    num_degree += 1
            num_remains += (num_degree / 2) - (num_node - 1)
        
        #判断是否可行：
        if num_component - 1 <= num_remains:
            return num_component - 1
        else:
            return -1


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

（4）网易2020年暑期实习编程第四题

有N个快递盒子，表示为[长，宽，高],数值均小于10000，要把小盒子装在大盒子里，一个盒子只能直接装一个盒子，问你你个盒子最多可包含多少个盒子（加上自己）

class Solution:

    def is_bigger(self, box1, box2):
        if box1[0] > box2[0] and box1[1] > box2[1] and box1[2] > box2[2]:
            return True
        return False

    # 以box当做节点深度遍历
    def dfs(self, box, cnt):
        if len(self.d[box]) == 0:
            # 更新最大深度
            self.max_cnt = max(self.max_cnt, cnt)
        for box in self.d[box]:
            # 如果box已经被访问了，说明是该box孩子的子孙，肯定深度没有之前大（该节点->孙子 小于 该节点->孩子->孩子）
            # 所以不用访问了
            if self.visit[box] == False:
                self.visit[box] = True
                self.dfs(box, cnt + 1)

    def maxBoxes(self, boxes):
        # write code here
        boxes = [(x[0], x[1], x[2]) for x in boxes]
        boxes = sorted(boxes, key=lambda x: x[0] * x[1] * x[2])
        import collections
        # d是记录每个box的孩子
        self.d = collections.defaultdict(list)
        box_cnt = len(boxes)
        # roots记录森林的根节点
        self.roots = [x for x in boxes]
        for i in range(box_cnt):
            for j in range(i + 1, box_cnt):
                if self.is_bigger(boxes[j], boxes[i]):
                    self.d[boxes[i]].append(boxes[j])
                    if boxes[j] in self.roots:
                        self.roots.remove(boxes[j])
        self.max_cnt = 1
        # visit作用见dfs函数
        self.visit = dict()
        for root in self.roots:
            # 每次遍历树，都要把所有节点置为未访问
            for i in range(box_cnt):
                self.visit[boxes[i]] = False
            self.root = root
            self.dfs(root, 1)
        return self.max_cnt
s = Solution()
boxes = [[5, 4, 3], [5, 4, 5], [6, 6, 6],[4, 3, 2]]
print(s.maxBoxes(boxes))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

5、DP

一、基本思想及实现

个人理解：

我的理解

所有的DP都可以使用递归来实现，往往来说，递归实现起来最简单；可以先从递归入手，找到最优子结构（就是核心的状态转移方程，如何从上一步——-》下一步），再尝试采用DP来求解。

关于二维DP和一维DP的分类

其实不是很重要；维数只是DP数组的维数，代表着DP数组存储的结果与多少个参数有联系；而并不是循环的次数，一般来说DP都是两层循环，根据题意可能增加循环层数。

程序流程

一般来说，最终写出来效率最高的是自底向上的迭代方法；该方法与递归的自顶向下有所不同，需要初始化DP数组，其一般步骤为：
（1）初始化DP[][]=0/±inf;根据边界条件获得部分DP数组的值，该值可以满足后续的计算的要求，即状态转移方程，右边的式子的每一项都可以在边界条件中找到
（2）根据影响DP数组结果的参数个数，确定循环层数，根据题意、一些边界条件，确定循环的起始和终止值，即DP数组的下标取值
（3）设置合理的条件，if（）：满足计算这一次的值

官方解释

DP适用问题：有最优子结构、子问题重叠

有最优子结构：原问题的最优解包含子问题的最优解
子问题重叠：子问题空间足够小，递归算法会反复求解相同的子问题，而不是产生新的子问题

几种实现方法：所有的DP都可以用递归实现

（1）自顶向下递归（一般不用，时间复杂度太大）
（2）自顶向下递归+备忘录(有时候备忘录的记录会比较复杂，详见本文leetcode5274)
（3）自底向上迭代（最为高效，但是边界条件有时候比较麻烦）

注意，lru_cache神器可以使得自顶向下的递归，获得近似于备忘录

from functools import lru_cache

class Solution:
    @lru_cache()
    def cuttingRope(self, n: int) -> int:
        if n == 2:
            return 1
        res = -1
        for i in range(1, n):
            res = max(res, max(i * self.cuttingRope(n - i),i * (n - i)))
        return res
1
2
3
4
5
6
7
8
9
10
11

《算法导论》钢条分割为例：讲解三种实现方法：

（1）

（2）


（3）

重构最优解：记录最优解的每一步的选择

二、几个典型的例子：

以下为面试典型题：参考
https://github.com/datawhalechina/Daily-interview/blob/master/coding/dp.md

此处所说的一维或二维dp指的只是使用的空间：一维dp是元素列表，二维dp是数组；而不是算法的复杂度

1、一维DP[i]

（1）leetcode300. 最长上升子序列

核心代码

    dp = [1] * size
            for i in range(1, size):
                for j in range(i):
                    if nums[i] > nums[j]:
                        
                        dp[i] = max(dp[i], dp[j] + 1)
            # 最后要全部走一遍，看最大值
            return max(dp)
1
2
3
4
5
6
7
8

（2）leetcode368. 最大整除子集

给出一个由无重复的正整数组成的集合，找出其中最大的整除子集，子集中任意一对 (Si，Sj) 都要满足：Si % Sj = 0 或 Sj % Si = 0。

如果有多个目标子集，返回其中任何一个均可。

与之前的不同之处，这一题不是求最大子集的元素个数，而需要重构最优解：

    class Solution(object):
        def largestDivisibleSubset(self, nums):
            """
            :type nums: List[int]
            :rtype: List[int]
            """
    
            if not nums: return nums
            if len(nums) == 1: return nums
            l = len(nums)
            nums.sort()
    
            dp = [1]*l
           
           #核心代码与最长上升子序列类似 
            for i in range(1, l):
                for j in range(i):
                    if not nums[i]%nums[j]:
                        dp[i] = max(dp[j] + 1, dp[i])
           
            #重构最优解
            maxl=max(dp)
            ans=[]
            for i in range(l-1,-1,-1):
                if maxl==dp[i]:
                    if not ans:
                        ans.append(nums[i])
                        maxl-=1
                    elif not ans[-1]%nums[i]:
                        ans.append(nums[i])
                        maxl-=1
            return ans[::-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

（3）leetcode121：买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
状态转移方程
前i日最大利润=max(前(i−1)日最大利润,第i日价格−前i日最低价格)
代码：
迭代的同时维持价格最小，利润最大

     class Solution:
        def maxProfit(self, prices: List[int]) -> int:
            maxprofit=0
            minprice=1<<31
            for i in range(1,len(prices)):
                minprice=min(minprice,prices[i-1])
                maxprofit=max(maxprofit,prices[i]-minprice)
            return maxprofit
1
2
3
4
5
6
7
8

（4）leetcode49. 丑数

我们把只包含因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:

1 是丑数。
n 不超过1690。

class Solution {
    public int nthUglyNumber(int n) {
        int dp[]=new int[1690];
        dp[0]=1;
        int idx2=0,idx3=0,idx5=0;
        int n2,n3,n5;
        for (int i=1;i<n;i++){
            n2=dp[idx2]*2;n3=dp[idx3]*3;n5=dp[idx5]*5;
            dp[i]=Math.min(Math.min(n2,n3),n5);
            if (dp[i]==n2) idx2++;
            if (dp[i]==n3) idx3++;
            if (dp[i]==n5) idx5++;
        }
        return dp[n-1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

（5）leetcode面试题48. 最长不含重复字符的子字符串

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

示例 1:

输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

解析
我刚开始的想法是，使用一个队列，依次遍历字符；如果该字符包含在队列中，则队头出队直到遇到队头元素和该字符相同；如果字符不在队列中，则字符入队；每次统计队列长度；这样的空间复杂度和时间复杂度都是O(n)

但是看到了大佬的解析，使用动规，把空间复杂度再压缩到O(1)

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> dic = new HashMap<>();
        int res = 0, tmp = 0;
        for(int j = 0; j < s.length(); j++) {
            int i = dic.containsKey(s.charAt(j)) ? dic.get(s.charAt(j)) : -1; // 获取索引 i
            dic.put(s.charAt(j), j); // 更新哈希表
            tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
            res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2、二维DP[i][j]

（1）最长公共子序列LCS

核心分析：


核心代码

    int lcs(string &A, string &B) {
            int dp[A.size()+1][B.size()+1] = {0};   
            for(int i=1;i<=A.size();i++){
                for(int j=1;j<=B.size();j++){
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
                    if(A[i-1] == B[j-1]){
                        dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
                    }
                }
            }
            return dp[A.size()][B.size()];
        }
1
2
3
4
5
6
7
8
9
10
11
12

（2）最长公共子串

与LCS不同，最长公共子串需要连续，对于两个字符串X和Y，长度分别为m,n，初始化c为（m+1）*（n+1）的矩阵
（1）如果i=0或者j=0：即其中一个长度为0，则c=0
（2）最后一个字符相同，即xi=yj，则c[i][j]=c[i-1][j-1]+1
（3）如果xi！=yj，由于子串需要连续，因此，c[i][j]=0

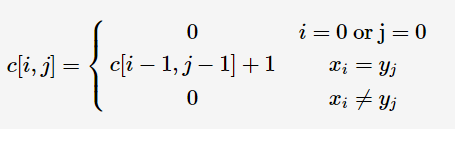
代码：

    class LongestSubstring:
        def findLongest(self, A, B):
            # write code here
            n,m=len(A),len(B)
            maxl=0
            dp=[[0]*(m+1) for _ in range(n+1)]
            for i in range(1,n+1):
                for j in range(1,m+1):
                    if A[i-1]==B[j-1]:
                        dp[i][j]=dp[i-1][j-1]+1
                        # maxl=max(maxl,dp[i][j])
    
                        # 重构解
                        if maxl<dp[i][j]:
                            maxl=dp[i][j]
                            endi = i
                    else:
                        dp[i][j]=0
            return maxl,A[endi-maxl:endi]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

（3）最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: “babad”
输出: “bab”
注意: “aba” 也是一个有效答案。
动态规划：

代码：

    class Solution:
        def longestPalindrome(self, s: str) -> str:
            if not s:
                return ''
            maxl=1
            start=0
            l=len(s)
            dp=[[False]*l for _ in range(l)]
            # init dp，初始化长度为1、2的回文串
            for i in range(l):
                dp[i][i]=True
                if i+1<l and s[i]==s[i+1]:
                    dp[i][i+1]=True
                    maxl=2
                    start=i
    		#判断长度大于等于3的回文串
            for ls in range(3,l+1):
                for i in range(l-ls+1):
                    j=i+ls-1
    
                    dp[i][j] =  dp[i+1][j-1] and s[i]==s[j]
                    # print(s[i:j+1],dp[i][j])
    
                    if dp[i][j] and j-i+1>maxl:
                        maxl=j-i+1
                        start=i
    
            return s[start:start+maxl]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

还有马拉车算法，复杂度为O(n)

非马拉车O(n)算法：源自牛客网

    class Solution:
        def longestPalindrome(self, s: str) -> str:
            if s == s[::-1]: return s
            maxLen = 0
            for i in range(len(s)):
                if i - maxLen >= 1 and s[i - maxLen - 1:i + 1] == s[i - maxLen - 1:i + 1][::-1]:
                    maxLen += 2
                    end = i
                    continue
                if i - maxLen >= 0 and s[i - maxLen:i + 1] == s[i - maxLen:i + 1][::-1]:
                    maxLen += 1
                    end=i
            return s[end-maxLen+1:end+1]
1
2
3
4
5
6
7
8
9
10
11
12
13

（4）leetcode5265. 可被三整除的最大和

给你一个整数数组 nums，请你找出并返回能被三整除的元素最大和。

示例 1：

输入：nums = [3,6,5,1,8]
输出：18
解释：选出数字 3, 6, 1 和 8，它们的和是 18（可被 3 整除的最大和）。
两种解法：

• 贪心：
  不考虑整除3的最大和一定是所有数字的和，那么就在该基础上减去最小的值，使得其可以被3整除；在寻找最小的数时需要做一些判断
• 动规
  转移方程：dp[i][j]代表考虑前i个数字，除3余j的最大和；
  转移方程表达的是：对于第nums[i]考虑加和不加两种情况的最大值：
  如果不加，则dp[i][j]=dp[i-1][j]；
  如果加，则应该从余数为(j-nums[i-1])%3转移到余数为j（即j%3），此时和要加上nums[i-1]

dp[i][j]=max(dp[i-1][j],dp[i-1][((j-nums[i-1])%3]+nums[i-1])

由于(j-nums[i])%3可能产生负数，因此可以需要做些处理：

把余数+3再模除3
dp[i][j]=max(dp[i-1][j],dp[i-1][((j-nums[i-1])%3+3)%3]+nums[i-1])
或者，根据正向思路直接写等式
dp[i][(j+nums[i])%3] = max(dp[i - 1][(j+nums[i-1])%3],dp[i -1][j] + nums[i - 1])

注意：初始化条件，在初始化时考虑迭代处理时max操作，需要将所有除dp[0][0]外的数据初始化为-inf

以下为代码：

class Solution:
    def maxSumDivThree(self, nums) -> int:
        l=len(nums)
        dp=[[float("-inf")]*3 for _ in range(l+1)]
        dp[0][0]=0
        for i in range(1,l+1) :
            for j in range(3):
                # dp[i][j]=max(dp[i-1][j],dp[i-1][((j-nums[i-1])%3+3)%3]+nums[i-1])
                dp[i][(j+nums[i-1])%3] = max(dp[i - 1][(j+nums[i-1])%3],dp[i -1][j] + nums[i - 1])
        return dp[l][0]
1
2
3
4
5
6
7
8
9
10

优化空间复杂度

我们还可以发现，所有的 f[i][…] 只会从 f[i - 1][…] 转移得来，因此我们在动态规划时只存储这两行的结果，减少空间复杂度。

        dp=[float("-inf")]*3
        dp[0]=0
        for num in nums:
            dpnext=dp[:]
            for i in range(3):
                dpnext[(i+num)%3]=max(dp[(i+num)%3],dp[i]+num)
            dp=dpnext
        return dp[0]
1
2
3
4
5
6
7
8

（5）5274. 停在原地的方案数

有一个长度为 arrLen 的数组，开始有一个指针在索引 0 处。

每一步操作中，你可以将指针向左或向右移动 1 步，或者停在原地（指针不能被移动到数组范围外）。

给你两个整数 steps 和 arrLen ，请你计算并返回：在恰好执行 steps 次操作以后，指针仍然指向索引 0 处的方案数。

由于答案可能会很大，请返回方案数 模 10^9 + 7 后的结果。
示例 1：

输入：steps = 3, arrLen = 2
输出：4
解释：3 步后，总共有 4 种不同的方法可以停在索引 0 处。
向右，向左，不动
不动，向右，向左
向右，不动，向左
不动，不动，不动
示例 2：

输入：steps = 2, arrLen = 4
输出：2
解释：2 步后，总共有 2 种不同的方法可以停在索引 0 处。
向右，向左
不动，不动

提示：
1 <= steps <= 500
1 <= arrLen <= 10^6

思路：
dp[i][j]表示花费j步走到第i个位置的所有方案数，
dp[i][j]的来源有三种，左边位置往右一步、右边位置往左一步以及原地不动，对于两端只有两种来源
状态转移方程为：
dp[i][j] = (dp[i][j - 1] + dp[i + 1][j - 1]) % mod, i == 0;
dp[i][j] = (dp[i][j - 1] + dp[i + 1][j - 1]) % mod, i == arrLen - 1，即到数组末尾;
dp[i][j] = (dp[i][j - 1] + dp[i][j - 1] + dp[i + 1][j - 1]) % mod, 其它位置;

class Solution:
    def numWays(self, steps: int, arrLen: int) -> int:
        arrLen=min(arrLen,steps) #为了降低空间复杂度和减少内层循环数
        dp = [[0] * arrLen for i in range(steps + 1)]
        dp[0][0]=1

        for i in range(1,steps+1):
            for j in range(arrLen):
                if j==0:
                    dp[i][j] = (dp[i-1][j ] + dp[i-1][j + 1])
                elif j==arrLen-1:
                    dp[i][j]=dp[i-1][j]+dp[i-1][j-1]
                else:
                    dp[i][j] = dp[i - 1][j - 1] +dp[i -1][j ] + dp[i-1][j +1]
        return dp[steps][0]%int((1e9+7))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

注意10^9=1e9, 但是python中%运算可以用于浮点数，运算结果可能与实际不符（这个问题把我坑了，调了好久bug）
写成：%int((1e9+7))或者 109+7**

• 备忘录的递归方法：

这个是我刚开始采用的，但是发现时间降不下来，经过反复调试发现，其实在我的递归过程中第一次备忘记录是发生在最复杂的情况求解出来，这样其实根本就没有得到优化：
我的代码如下：

class Solution2:
    def numWays(self, steps: int, arrLen: int) -> int:
        st=[[False for i in range(steps+1)] for _ in range(arrLen)]
        def onestep(stepnum, curidx):

            if stepnum >= steps:
                st[curidx][stepnum]=1 if curidx == 0 else 0
                return st[curidx][stepnum]
            if st[curidx][stepnum]:
                return st[curidx][stepnum]

            if curidx==0:
                st[curidx][stepnum]=onestep(stepnum + 1, (curidx + 1))+onestep(stepnum + 1, (curidx))
                return st[curidx][stepnum]
            elif curidx==arrLen-1:
                st[curidx][stepnum]=onestep(stepnum + 1, (curidx)) + onestep(stepnum + 1, (curidx - 1))
                return st[curidx][stepnum]
            else:
                st[curidx][stepnum] =onestep(stepnum + 1, (curidx + 1)) + onestep(stepnum + 1, (curidx)) + onestep(stepnum + 1,(curidx - 1))%(10e9+7)
                return st[curidx][stepnum]
        return onestep(0, 0)%int(1e9+7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

然后发现了别人的备忘录递归：
感觉这么复杂还不如直接递归dp。。。。。

class Solution:
    def __init__(self):
        self.result_dict = dict()

    def numWays(self, steps: int, arrLen: int) -> int:
        cnt = self.helper(steps, 0, arrLen, 0)
        return cnt % (10**9 + 7)

    def helper(self, step_sy, point_add, arrlen, count):
        if step_sy == 0 and point_add == 0:
            count += 1
            self.result_dict.update({(step_sy, point_add): count})
            return count

        if step_sy >= point_add and point_add < arrlen and point_add >= 0:
            if (step_sy-1, point_add) in self.result_dict:
                c1 = self.result_dict[(step_sy-1, point_add)]
            else:
                c1 = self.helper(step_sy-1, point_add, arrlen, count)
            if (step_sy-1, point_add+1) in self.result_dict:
                c2 = self.result_dict[(step_sy-1, point_add+1)]
            else:
                c2 = self.helper(step_sy-1, point_add+1, arrlen, count)
            if (step_sy-1, point_add-1) in self.result_dict:
                c3 = self.result_dict[(step_sy-1, point_add-1)]
            else:
                c3 = self.helper(step_sy-1, point_add-1, arrlen, count)
            self.result_dict.update({(step_sy, point_add): c1 + c2 + c3})
            return c1 + c2 + c3
        else:
            return count
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

三、遇到的其他题目

leetcode1155. 掷骰子的N种方法

这里有 d 个一样的骰子，每个骰子上都有 f 个面，分别标号为 1, 2, …, f。

我们约定：掷骰子的得到总点数为各骰子面朝上的数字的总和。

如果需要掷出的总点数为 target，请你计算出有多少种不同的组合情况（所有的组合情况总共有 f^d 种），模 10^9 + 7 后返回。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-dice-rolls-with-target-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例 5：

输入：d = 30, f = 30, target = 500
输出：222616187

题目分析：
最开始想的就是递归实现，自顶向下的写法最容易想到，已知d个骰子，目标数为target，那最后一个数就有f种可能，假设为k，减去最后一个数，剩下的target-k为d-1个骰子的和，依次自顶向下递归，

由于每次递归，骰子数目会减一，最后到终止条件d=1时，若剩下的target>f，那么这种情况不可能，返回0，若target<=f那个最后一个骰子值为target，为一种情况，返回1；

再就是加一些边界条件，不可能的情况。

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int) -> int:
        def fun(d,f,tar):
            if d==1 :
                if f>=tar:
                    return 1
                else:
                    return 0
            elif d>tar or d*f<tar:
                return 0

            else:
                s=0
                for i in range(1,f+1):
                	#边界条件
                	if tar-i>0:
                    	s+=fun(d-1,f,tar-i)
                return s%(10**9+7)
        return fun(d,f,target)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

但是很不幸，一看这个复杂度，每次递归会重新调用f次自身，o(d^f)复杂度，leetcode过了4/65case当然不行，该如何优化呢--------第一个方法：加备忘录

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int) -> int:
        #备忘录
        lst=[[0]*1001 for _ in range(31)]
        def fun(d, f, tar):
        #             从备忘录中取
            if lst[d][tar] != 0:
                return lst[d][tar]
                #终止条件
            if d == 1:
                if f >= tar:
                    lst[d][tar] = 1
                    return 1
                else:
                    lst[d][tar] = 0
                    return 0
            elif d>tar or d*f<tar:
                lst[d][tar]=0
                return 0
            else:
                s = 0
                for i in range(1, f + 1):
                    if tar-i>0:
                        s += fun(d - 1, f, tar - i)
                lst[d][tar] = s % (10 ** 9 + 7)
            return lst[d][tar]
        return fun(d, f, target)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

这样就过了，再来优化，就是自底向上的迭代的方法，该方法比较麻烦的一点就是，需要判断d和target的迭代范围：
看起来非常简洁，但是刚开始不容易想到

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int) -> int:
        a=[[0]*1001 for _ in range(31)]
#         初始化数组
        for i in range(1,f+1):
            a[1][i]=1
            #迭代求解
        #骰子数：从2----d
        for i in range(2,d+1):
        #目标数：从最小为i个骰子都为1，到i个骰子都为f
            for j in range(i,i*f+1):
            #重复加f次
                for k in range(1,f+1):
                    if j-k>0:
                        a[i][j]+=a[i-1][j-k]
                    a[i][j]=a[i][j]%(10**9+7)
        return a[d][target]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

leetcode89. 格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

示例 1:
输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/gray-code
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

• 解法1：动态规划，根据0阶格雷码依次按照规律求解n阶格雷码。求解规律没有那么简单，不容易找到：在n阶格雷码基础上，添加n阶格雷码倒序后每个码的首位添加1的值，得到n+1所有格雷码

来自题解：https://leetcode-cn.com/problems/gray-code/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by–12/

（1）n=0 ：解为0
（2）n = 1 的解：0 、1
（3）n = 2 的解
00 - 0
10 - 2
11 - 3
01 - 1
（4）n = 3 的解
000 - 0
010 - 2
011 - 3
001 - 1
------------
101 - 5
111 - 7
110 - 6
100 - 4

class Solution:
    def grayCode(self, n: int) -> List[int]:
        gray=[0]
        for i in range(n):
            add=1<<i
            l=len(gray)
            for j in range(l-1,-1,-1):
                gray.append(gray[j]+add)
        return gray
1
2
3
4
5
6
7
8
9

• 解法2：回溯，按照某种规律生成格雷码，以防止无法出现闭环的情形，参考leetcode上https://leetcode-cn.com/problems/gray-code/solution/jian-dan-de-si-lu-44ms-by-dannnn/ 思路

从空字符串开始，上面的（绿色）分别加0、1，下面的（红色）分别加1、0，直到长度达n

class Solution:
     def grayCode(self, n: int) -> List[int]:
        if n==0:
            return [0]
        gray=[]
        def back(now,op):
            if len(now)==n:
                gray.append(int(now,2))
            elif op==0:
                back(now+'0',0)
                back(now+'1',1)
            else:
                back(now+'1',0)
                back(now+'0',1)
        back("",0)
        return gray
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

6、贪心算法

应用条件：最优子结构

（2）leetcode1014：最佳观光组合

给定正整数数组 A，A[i] 表示第 i 个观光景点的评分，并且两个景点 i 和 j 之间的距离为 j - i。

一对景点（i < j）组成的观光组合的得分为（A[i] + A[j] + i - j）：景点的评分之和减去它们两者之间的距离。

返回一对观光景点能取得的最高分。

示例：

输入：[8,1,5,2,6]
输出：11
解释：i = 0, j = 2, A[i] + A[j] + i - j = 8 + 5 + 0 - 2 = 11

思路：
维持A[i] + i最大的同时，维持A[i] + i +A[j] - j 最大，由于j>i，因此，初始化left=A[0],迭代从1开始，维持A[i] + i +A[j] - j最大在前

    class Solution:
        def maxScoreSightseeingPair(self, A: list) -> int:
            left, res = A[0], -1
            for j in range(1, len(A)):
                res = max(res, left + A[j] - j)
                left = max(left, A[j] + j)
            return res
1
2
3
4
5
6
7

（3）nowcoder：给定整数序列求连续子串最大和

链接：https://www.nowcoder.com/questionTerminal/9d216205fbb44e538f725d9637239523
来源：牛客网
给定无序整数序列，求连续子串最大和，例如{-23 17 -7 11 -2 1 -34}，子串为{17,-7,11}，最大和为21
输入描述:
输入为整数序列，数字用空格分隔，如：-23 17 -7 11 -2 1 -34
输出描述:
输出为子序列的最大和：21

    while 1:
        try:
            nums=list(map(int,input().split()))
            maxs=float('-inf')
            curs=0
            for i in range(len(nums)):
                if curs>=0:
                    curs+=nums[i]
                else:
                    curs=nums[i]
                maxs=max(maxs,curs)
            print(maxs)
        except:
            break
1
2
3
4
5
6
7
8
9
10
11
12
13
14

拓展1：
增加条件，子串中连续的0不超过3个：（字节跳动2018暑期营算法笔试）
给出一个长度为 n 的数组a1、a2、…、an

输入描述：
第一行一个正整数 n, 表示数组长度，1 <= n <= 1000000。
第二行 n 个正整数，a1a2…an

输出描述：
一个整数
示例1：
输入
6
15 0 0 0 0 20
输出
20

拓展2：
给定一个整数数组，找出两个 不重叠 子数组使得它们的和最大。（lintcode42）
每个子数组的数字在数组中的位置应该是连续的。
返回最大的和。
给出数组 [1, 3, -1, 2, -1, 2]
这两个子数组分别为 [1, 3] 和 [2, -1, 2] 或者 [1, 3, -1, 2] 和 [2]，它们的最大和都是 7

    class Solution {
    public:
        /**
         * @param nums: A list of integers
         * @return: An integer denotes the sum of max two non-overlapping subarrays
         */
        int maxTwoSubArrays(vector<int> nums) {
            // write your code here
            int result = nums[0],sum = 0;
            vector<int> left(nums.size(),0),right(nums.size(),0);
            for (int i = 0;i < nums.size();i++) {
                sum += nums[i];
                result = max(result,sum);
                sum = max(sum,0);
                left[i] = result;
            }
            sum = 0,result = nums[nums.size()-1];
            for (int i = nums.size()-1;i > 0;i--) {
                sum += nums[i];
                result = max(result,sum);
                sum = max(sum,0);
                right[i] = result;
            }
            result = INT_MIN;
            for (int i = 0;i < nums.size()-1;i++) {
                result = max(result,left[i] + right[i+1]);
            }
            return result;
        }
    };
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

扩展3:
给定一个整数数组，找出两个不重叠的子数组A和B，使两个子数组和的差的绝对值|SUM(A) - SUM(B)|最大。

7、排序算法

更好的总结：https://blog.csdn.net/hellozhxy/article/details/79911867

掌握：
快排：
归并排序：分治思想
堆排序：

8、回溯

回溯基本思想

简介

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

基本思想

在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。

若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。

而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

例题

leetcode46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

解题思路：

解法一：

class Solution:
    def permute(self, nums):
        def backtrack(first = 0):
            # 递归终止条件
            if first == n:  
                output.append(nums[:])
            for i in range(first, n):
                # place i-th integer first 
                # 交换当前和第一个数字
                nums[first], nums[i] = nums[i], nums[first]
                # use next integers to complete the permutations
                backtrack(first + 1)
                # backtrack，回溯，还原上一步
                nums[first], nums[i] = nums[i], nums[first]
        
        n = len(nums)
        output = []
        backtrack()
        return output


#类似的解法
class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        
        l=len(nums)
        v=[True]*l
        ans=[]
        q=[]
        def dfs(x):
            if x>=l:
                ans.append(q.copy())
            for i in range(l):
                if v[i]:
                    q.append(nums[i])
                    v[i]=False
                    dfs(x+1)
#                     当x+1>l, 即x=l时，ans才会重新添加
                    
                    v[i]=True
                    q.pop()
        dfs(0)
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

解法二：使用库函数

def permute(self, nums: List[int]) -> List[List[int]]:
        return list(itertools.permutations(nums))
1
2

leetcode78.子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

#解法一：回溯
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        n = len(nums)
        
        def helper(i, tmp):
            res.append(tmp)
            for j in range(i, n):
                helper(j + 1,tmp + [nums[j]] )
        helper(0, [])
        return res  
#解法2：库函数：
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        for i in range(len(nums)+1):
            for tmp in itertools.combinations(nums, i):
                res.append(tmp)
        return res

#解法3，迭代
class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = [[]]
        for i in nums:
            res = res + [[i] + num for num in res]
        return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

leetcode5240. 串联字符串的最大长度

给定一个字符串数组 arr，字符串 s 是将 arr 某一子序列字符串连接所得的字符串，如果 s 中的每一个字符都只出现过一次，那么它就是一个可行解。

请返回所有可行解 s 中最长长度。

输入：arr = [“cha”,“r”,“act”,“ers”]
输出：6
解释：可能的解答有 “chaers” 和 “acters”。

• 回溯算法，采用递归实现，递归标记当前运行到第i个字符；和当前的满足条件的最长字符tmp；从i到i+1个字符；可以选择：

1. 如果not (set(tmp) & set(arr[i]))；即字符不重复，可以选择添加或者不添加（不添加可能后面有更长的s）
2. 如果字符重复，则只能选择不添加
3. 终止条件，递归到l+1字符

class Solution():
    def maxLength(self, arr):
        arr=list(filter(lambda x: len(set(x)) == len(x),arr))
        def dfs(i, tmp):

            if i >= len(arr):
                return len(tmp)
            else:
                if not (set(tmp) & set(arr[i])):
                    return max(dfs(i+1,tmp+arr[i]),dfs(i+1,tmp))
                else:
                    return dfs(i + 1, tmp)

        l=dfs(0,'')
        return l
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

-------------其他数据结构或方法的活用---------------------

10、栈的活用：

（1）实现递归算法：二叉树DFS

栈这种数据结构，是计算机为实现子程序调用，实现的数据结构，天然的可以想到栈可以用于替代实现递归算法。
如：二叉树的DFS的实现

（2）按照运算规则计算表达式（含有嵌套），字符匹配

牛客网：表达式求值

给定一个字符串描述的算术表达式，计算出结果值。
牛客连接https://www.nowcoder.com/profile/216430209/myFollowings/detail/7783335
输入字符串长度不超过100，合法的字符包括”+, -, *, /, (, )”，”0-9”，字符串内容的合法性及表达式语法的合法性由做题者检查。本题目只涉及整型计算

"""
中缀表达式转换为后缀表达式(去括号)
"""
 
# exp = "5*(9+(3-1)*3+10/2)"
exp =input()
# exp='(7+5*4*3+6)'
 
def campare(op1,op2):
    return op1 in ["*", "/"] and op2 in ["+", "-"]
 
houzhui=[]
opt=[]
i=0
while i<len(exp):
    # 若是数字就输出至后缀表达式
    if exp[i].isdigit():
        start=i
        # 一定是用i+1来判断后一个字符是否为数字，否则指针位置不对
        # 判断长度的条件在前
        while i+1<len(exp) and exp[i+1].isdigit() :
            i+=1
        end=i+1
        num=int(exp[start:end])
        # print(num)
        houzhui.append(num)
    #左括号则入操作符栈
    elif exp[i]=='(':
        opt.append('(')
    # 右括号，将操作符栈元素依次弹栈至后缀表达式，直到栈顶为“（”，并将“（”弹栈
    elif exp[i]==')':
        while opt[-1]!='(':
            houzhui.append(opt.pop())
        opt.pop()
    # 为运算符，
    elif exp[i] in ['+','-','*','/']:
        # opt有三种情况，都将运算符入opt栈
        # 栈空、栈顶为（，符号优先级比栈顶符号高
        if opt==[] or opt[-1]=='(' or campare(exp[i],opt[-1]):
            opt.append(exp[i])
 
        else:
            # 否则，将opt弹栈输出，直到opt为空,左括号出现,或者操作符栈顶元素优先级更高，
            # 再将该运算符入opt栈
            while not(opt==[] or opt[-1]=='(' or campare(exp[i],opt[-1])):
                houzhui.append(opt.pop())
            opt.append(exp[i])
    # print(houzhui)
    # print(opt)
    i+=1    #指针加一
# 最后将opt剩余运算符依次弹出输出
for i in range(len(opt)):
    houzhui.append(opt.pop())
    # print(houzhui)
    # print(opt)
# print('-----------------')
"""
后缀表达式运算
 
"""
def getvalue(num1,num2,op):
    if op == "+":
        return num1 + num2
    elif op == "-":
        return num1 - num2
    elif op == "*":
        return num1 * num2
    else:  # /
        return num1 / num2
 
# print(houzhui)
 
value=[]
i=0
while len(houzhui):
    if houzhui[i] in ['+','-','*','/']:
        op=houzhui.pop(0)
        num2=value.pop()
        num1=value.pop()
        value.append(getvalue(num1, num2, op))
    else:
        value.append(houzhui.pop(0))
    # print(houzhui)
    # print(value)
# print(houzhui)
print(value.pop())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

也可以简化程序，把中缀转后缀表达式 与 表达式计算一起做

字节跳动2019暑期夏令营，第一道编程题：

leetcode周赛142 花括号展开II：

https://leetcode-cn.com/contest/weekly-contest-142/problems/brace-expansion-ii/
如果你熟悉 Shell 编程，那么一定了解过花括号展开，它可以用来生成任意字符串。

花括号展开的表达式可以看作一个由 花括号、逗号 和 小写英文字母 组成的字符串，定义下面几条语法规则：

如果只给出单一的元素 x，那么表达式表示的字符串就只有 “x”。
例如，表达式 {a} 表示字符串 “a”。
而表达式 {ab} 就表示字符串 “ab”。
当两个或多个表达式并列，以逗号分隔时，我们取这些表达式中元素的并集。
例如，表达式 {a,b,c} 表示字符串 “a”,“b”,“c”。
而表达式 {a,b},{b,c} 也可以表示字符串 “a”,“b”,“c”。
要是两个或多个表达式相接，中间没有隔开时，我们从这些表达式中各取一个元素依次连接形成字符串。
例如，表达式 {a,b}{c,d} 表示字符串 “ac”,“ad”,“bc”,“bd”。
表达式之间允许嵌套，单一元素与表达式的连接也是允许的。
例如，表达式 a{b,c,d} 表示字符串 “ab”,“ac”,"ad"​​​​​​。
例如，表达式 {a{b,c}}{{d,e}f{g,h}} 可以代换为 {ab,ac}{dfg,dfh,efg,efh}，表示字符串 “abdfg”, “abdfh”, “abefg”, “abefh”, “acdfg”, “acdfh”, “acefg”, “acefh”。

class Solution2:
    def braceExpansionII(self, expression: str):
        expression = "{" + expression + "}"
        stack = []
        i = 0
        while i < len(expression):
            c = expression[i]
            if c == '{':
                stack.append(c)
                i += 1
            elif c == ',':
                stack.append(c)
                i += 1
            elif c == '}':
                ans = stack.pop()
                while stack[-1] != '{':
                    if stack[-1] == ',':
                        stack.pop()
                        #采用集合存储字母，集合并集做运算
                        ans = ans | stack.pop()

                stack.pop()

                while stack and stack[-1] != ',' and stack[-1] != '{':
                    #串连字符的判定条件：在做完一个{}运算后，栈顶有集合元素，如ans={‘s’，‘e’}，栈顶={‘s’}
                    temp = stack.pop()
                    res = set()
                    for pre in temp:
                        for suf in ans:
                            res.add(pre+suf)
                    ans = res
                stack.append(ans)
                i += 1
            else:
                start = i
                while i < len(expression) and expression[i] not in {'{', '}', ','}:
                    i += 1
                string = expression[start:i]
                ans = {string}
                while stack and stack[-1] != ',' and stack[-1] != '{':
                #串连字符的判定条件：{}直接连接字符，如{s,c}a
                    temp = stack.pop()
                    res = set()
                    for pre in temp:
                        for suf in ans:
                            res.add(pre+suf)
                    ans = res
                stack.append(ans)
        return sorted(list(stack[0]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

leetcode周赛5249. 移除无效的括号

给你一个由 ‘(’、’)’ 和小写字母组成的字符串 s。

你需要从字符串中删除最少数目的 ‘(’ 或者 ‘)’ （可以删除任意位置的括号)，使得剩下的「括号字符串」有效。

请返回任意一个合法字符串。

有效「括号字符串」应当符合以下 任意一条 要求：

空字符串或只包含小写字母的字符串
可以被写作 AB（A 连接 B）的字符串，其中 A 和 B 都是有效「括号字符串」
可以被写作 (A) 的字符串，其中 A 是一个有效的「括号字符串」

示例 1：

输入：s = “lee(t©o)de)”
输出：“lee(t©o)de”
解释：“lee(t(co)de)” , “lee(t©ode)” 也是一个可行答案。
示例 2：

输入：s = “a)b©d”
输出：“ab©d”
示例 3：

输入：s = “))((”
输出：""
解释：空字符串也是有效的
示例 4：

输入：s = “(a(b©d)”
输出：“a(b©d)”

class Solution:
    def minRemoveToMakeValid(self, s: str) -> str:
        l=len(s)
        stack=[]
        flag=[False for _ in range(l)]
        for i in range(l):
            if s[i].isalpha():
                flag[i]=True
            elif s[i]=="(":
                stack.append(('(',i))
                continue
            elif s[i]==")" and stack and stack[-1][0]=='(':
                _,idx=stack.pop()
                flag[i]=True
                flag[idx]=True
        ans=''
        for i in range(l):
            if flag[i]:
                ans+=s[i]
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

总结：

解题步骤：
（1）查看表达式的类型：
前缀和后缀都能很方便的进行判断和求解（利用（）和，等分隔符，可以很有效的提取出运算的数据和参与的运算类型）；
中缀稍微麻烦一些，需要做一些判定
对于以上两类表达式，应将运算符和非运算符分开存放，方便判断

其余类别不清晰的表达式如花括号展开，其实是集合的运算，运算符有些还可以省略，则需要根据情况处理
（2）查看数据类型：确定数据存储形式
对于数字类，参与数值运算，可以直接存
对于字符类，参与布尔运算，判定后存储为布尔变量
对于字符型，参与集合运算，可以以集合set（）形式存储
（3）什么时候开始运算？
一般是反括号，}，],)等；
注意：
需不需要外层括号
一元和多元运算
弹栈和入栈（无用数据出栈，计算结果入栈）

（3）维护递增（递减）栈，类似于贪心

leetcode1081. 不同字符的最小子序列:

返回字符串 text 中按字典序排列最小的子序列，该子序列包含 text 中所有不同字符一次。

示例 1：

输入：“cdadabcc”
输出：“adbc”
示例 2：

输入：“abcd”
输出：“abcd”
示例 3：

输入：“ecbacba”
输出：“eacb”
示例 4：

输入：“leetcode”
输出：“letcod”
https://leetcode-cn.com/problems/smallest-subsequence-of-distinct-characters/solution/tan-xin-suan-fa-zhan-wei-yan-ma-python-dai-ma-java/
采用栈的结构，实现对历史最小字符的记录，

class Solution:
    def smallestSubsequence(self, text: str) -> str:
        size = len(text)
        stack = []
        for i in range(size):
            if text[i] in stack:
            #已经在stack中，不作处理，继续循环
                continue
            while stack and ord(text[i]) < ord(stack[-1]) and \
                    text.find(stack[-1], i) != -1:#这一句用于判断索引i以后还有该字符，该字符才可被弹出
                stack.pop()
            stack.append(text[i])
        return ''.join(stack)

1
2
3
4
5
6
7
8
9
10
11
12
13
14

11、堆 /二叉堆（满足特殊要求的二叉树）

堆：又叫二叉堆，利用完全二叉树的结构来维护一组数据
按照父亲节点和孩子节点的特性，又分为最大堆和最小堆

最大堆：父节点的值>=子节点的值：用于堆排序

堆排序，直接调用

最小堆：父节点的值<=子节点的值：用于优先队列

（1）字节跳动2018校招算法

https://www.nowcoder.com/profile/216430209/test/24071106/141059#summary
产品经理(PM)有很多好的idea，而这些idea需要程序员实现。现在有N个PM，在某个时间会想出一个 idea，每个 idea 有提出时间、所需时间和优先等级。对于一个PM来说，最想实现的idea首先考虑优先等级高的，相同的情况下优先所需时间最小的，还相同的情况下选择最早想出的，没有 PM 会在同一时刻提出两个 idea。

同时有M个程序员，每个程序员空闲的时候就会查看每个PM尚未执行并且最想完成的一个idea,然后从中挑选出所需时间最小的一个idea独立实现，如果所需时间相同则选择PM序号最小的。直到完成了idea才会重复上述操作。如果有多个同时处于空闲状态的程序员，那么他们会依次进行查看idea的操作。

求每个idea实现的时间。

输入第一行三个数N、M、P，分别表示有N个PM，M个程序员，P个idea。随后有P行，每行有4个数字，分别是PM序号、提出时间、优先等级和所需时间。输出P行，分别表示每个idea实现的时间点。

class Solution:
    def pm_ideas(self):

        N, M, P = input().strip().split()
        N, M, P = int(N), int(M), int(P)
        ideas = []
        for i in range(P):
            pm_id, proposal_t, priority, duration = input().strip().split()
            pm_id, proposal_t, priority, duration = int(pm_id), int(proposal_t), int(priority), int(duration)
            ideas.append((proposal_t, pm_id, priority, duration, i))
        ideas.sort(reverse=True)
        #ideas按照提出时间降序排列


        pm = defaultdict(list)
        # 生成默认值为空列表的字典，键为pm——id，值为idea参数元祖构成的列表

        res = [0] * P
        # 返回值
        coders = [0] * M
        # 程序员时间空闲时刻
        heapq.heapify(coders)
        clock = 0
        # 当前时间
        available = 0
        # 候选队列中的idea数目

        while ideas or available > 0:
            coder_clock = heapq.heappop(coders)
            clock = max(clock, coder_clock)
            if available == 0:
                clock = max(clock, ideas[-1][0])
            # 当还有没处理的idea，最先提出的idea的提出时间小于等于当前clock，则把该idea加入pm对应地id的列表中
            while ideas and ideas[-1][0] <= clock:
                proposal_t, pm_id, priority, duration, idea_id = ideas.pop()
                heapq.heappush(pm[pm_id], (-priority, duration, pm_id, proposal_t, idea_id))
                # -priority排序，越小优先级越高
                available += 1

            candidates = []
            # 候选idea初始化
            for pm_id, tasks in pm.items():
                if tasks:
                    _, duration, pm_id, proposal_t, idea_id = tasks[0]
                    heapq.heappush(candidates, (duration, pm_id, proposal_t, idea_id))
            #         duration排序，越小，越优先处理

            if not candidates:
                break

            duration, pm_id, proposal_t, idea_id = heapq.heappop(candidates)
            heapq.heappop(pm[pm_id])
            available -= 1
            # 每次仅处理一个idea
            res[idea_id] = clock + duration
            heapq.heappush(coders, clock + duration)

        for i in range(P):
            print(res[i])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

12、双指针

（1）快慢指针：

leetcode142. 环形链表 II：链表有无环，环所在节点

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

• 暴力法：将节点引用变量存入list中，while循环判断下一个节点是否在list中
• 快慢指针：普通快慢指针，快指针比慢指针快两倍，如果有环，快指针一定会追上慢指针——可以用来判断是否有环；如果需要求解环入口节点位置，需要两轮相遇

构建双指针第一次相遇：

• 快指针走了慢指针 22 倍的路程，即 f = 2sf=2s；（fast 每轮走 22 步，slow 每轮走 11 步）
• 快指针比慢指针多走了 nn 个环的长度，即 f = s + nbf=s+nb；（双指针都走过 aa 步，直到相遇 fast 比 slow
  多走整数倍环的长度）
• 代入可推出：f = 2nbf=2nb，s = nbs=nb，即快慢指针分别走了 2n2n，nn 个环的周长。

构建双指针第二次相遇：

• 将 fast 指针重新指向链表头部 head，slow 指针位置不变，此时 fast走了 00 步，slow 指针走了 nbnb 步；
• 令双指针一起向前走，两指针每轮都走 11 步；
• 当 fast 指针走到 aa 步时，slow 指针正好走到 a + nba+nb 步，此时 两指针重合并同时指向链表环入口
• 最终返回 fast 或 slow 即可。

作者：jyd
链接：https://leetcode-cn.com/problems/linked-list-cycle-ii/solution/linked-list-cycle-ii-kuai-man-zhi-zhen-shuang-zhi-/

第一轮相遇后，重置快指针在head处，以慢指针相同速度前进a步，此时可在入口处相遇

class Solution(object):
    def detectCycle(self, head):
        fast, slow = head, head
        while True:
            if not (fast and fast.next): 
                return
            fast, slow = fast.next.next, slow.next
            if fast == slow: 
                break
        fast = head
        while fast != slow:
            fast, slow = fast.next, slow.next
        return fast
1
2
3
4
5
6
7
8
9
10
11
12
13

（2）左右指针：寻找区间，优化暴力解法时间复杂度，

程序要点：移动终止条件？？（r>l,r<len）移动条件？？？左右指针如何移动？

leetcode11. 盛最多水的容器

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

思路：盛水的容量等于左右指针距离*最小高度；首先我们初始化左右指针距离最大，在缩小左右指针距离的时候，想要找到比之前盛水更多的方案，只有提高最小高度，那么这种情况下就要选择高度最小的指针内移。
o（n）时间负责度，比暴力法o(n2)的时间复杂度快

class Solution:
    def maxArea(self, height: List[int]) -> int:
        le,ri=0,len(height)-1
        val=(ri-le)*min(height[ri],height[le])        
        while le<ri:
            if height[le]<height[ri]:
                le+=1
            else:
                ri-=1
            val=max(val,(ri-le)*min(height[ri],height[le]))
        return val
1
2
3
4
5
6
7
8
9
10
11

leetcode15. 三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
[-1, 0, 1],
[-1, -1, 2]
]
暴力解法时间复杂度为on3，使用**排序+左右指针+**判定条件优化到on2

class Solution:
    def threeSum(self, nums: list) -> list:
        nums.sort()
        ans = []
        if not nums or len(nums)<3:
            return ans
        for i in range(len(nums)):
            if nums[i] > 0:
                return ans
            if i>0 and nums[i]==nums[i-1]:
                continue
            le = i + 1
            ri = len(nums) - 1
            while le < ri:
                sums = nums[i] + nums[le] + nums[ri]
                if sums == 0:
                    ans.append([nums[i], nums[le], nums[ri]])
                    while ri > le and nums[ri] == nums[ri - 1]:
                        ri -= 1
                    while ri > le and nums[le] == nums[le + 1]:
                        le += 1
                    le+=1
                    ri-=1
                elif sums > 0:
                    ri -= 1
                else:
                    le += 1
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

leetcode3. 无重复字符的最长子串

示例 3:

输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if not s:
            return 0
        sl=len(set(s))
        if sl==1 or sl==len(s):
            return sl
        l,r=0,1
        ans=1
        while r<len(s):
            if s[r] in s[l:r]:
                ans=max(r-l,ans)
                while r>l and s[r] in s[l:r]:
                    l+=1
            elif len(s)-1==r:
                ans=max(r-l+1,ans)
            r+=1   
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

13、位运算

与：某位置1

（1）判断奇偶：取x的最后一个二进制位：x & 1
拓展：取x的倒数第k位：x&(1<<k)
（2）判断有多少2进制1：消去末尾的1：x=x&(x-1)
（3）与0xffff相与，为自身

或：某位清零

（1）与0相或，为自身

异或：

性质： 两个相同的数异或为0，与0异或为自身

leetcode5304. 子数组异或查询

有一个正整数数组 arr，现给你一个对应的查询数组 queries，其中 queries[i] = [Li, Ri]。

对于每个查询 i，请你计算从 Li 到 Ri 的 XOR 值（即 arr[Li] xor arr[Li+1] xor … xor arr[Ri]）作为本次查询的结果。

并返回一个包含给定查询 queries 所有结果的数组。

示例 1：

输入：arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
输出：[2,7,14,8]
解释：
数组中元素的二进制表示形式是：
1 = 0001
3 = 0011
4 = 0100
8 = 1000
查询的 XOR 值为：
[0,1] = 1 xor 3 = 2
[1,2] = 3 xor 4 = 7
[0,3] = 1 xor 3 xor 4 xor 8 = 14
[3,3] = 8

解析：
刚开始只想到异或的交换律(a ^ b) ^ c=a ^ (b ^ c)；写了个递归，报内存不足，可能是递归深度太大；后年看解题，才知道利用递归的性质可以构造递归前缀和,来求部分异或 c ^ d= (a ^ b) ^ (a ^ b ^ c ^ d)

原始代码

class Solution:
    def xorQueries(self, arr: List[int], queries: List[List[int]]) -> List[int]:
        def getxor(st,end):
            if dp[st][end]!=-1:
                return dp[st][end]
            else:
                dp[st][end-1]=getxor(st,end-1)
                return dp[st][end-1]^arr[end]
        
        
        n=len(arr)
        dp=[[-1]*n for _ in range(n)]
        for i in range(n):
            dp[i][i]=arr[i]
        ans=[]
        for st,end in queries:
            ans.append(getxor(st,end))
        return ans

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

修改后

class Solution:
    def xorQueries(self, arr: List[int], queries: List[List[int]]) -> List[int]:
        xorlst=[0]
        for a in arr:
            xorlst.append(xorlst[-1]^a)
        # print(xorlst)
        ans=[]
        for st,end in queries:
            ans.append(xorlst[st]^xorlst[end+1])
        return ans
1
2
3
4
5
6
7
8
9
10

14、map/字典使用

leetcode5214. 最长定差子序列

给你一个整数数组 arr 和一个整数 difference，请你找出 arr 中所有相邻元素之间的差等于给定 difference 的等差子序列，并返回其中最长的等差子序列的长度。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-arithmetic-subsequence-of-given-difference
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

输入：arr = [1,5,7,8,5,3,4,2,1], difference = -2
输出：4
解释：最长的等差子序列是 [7,5,3,1]。

思路：
依次遍历每个数组元素，使用map存储到当前元素为止的最长等差数列长度；如果如果上一个元素（下一个元素—差）存在，则长度在其基础上加一；不存在则将键值置为1。输出map最大值

class Solution:
    def longestSubsequence(self, arr: List[int], difference: int) -> int:
        for a in arr:
            d[a] = d.get(a - difference, 0) + 1
        return max(d.values())
1
2
3
4
5

leetcode146 LRU缓存机制

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4

• 解题：hashmap+双端队列

https://leetcode-cn.com/problems/lru-cache/solution/lru-ce-lue-xiang-jie-he-shi-xian-by-labuladong/

代码参考
https://leetcode-cn.com/problems/lru-cache/solution/shu-ju-jie-gou-fen-xi-python-ha-xi-shuang-xiang-li/

class ListNode:
    def __init__(self, key=None, value=None):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None


class LRUCache:
    def __init__(self, capacity):
        self.capacity = capacity
        self.hashmap = {}
        # 新建两个节点 head 和 tail
        self.head = ListNode()
        self.tail = ListNode()
        # 初始化链表为 head <-> tail
        self.head.next = self.tail
        self.tail.prev = self.head

    # 因为get与put操作都可能需要将双向链表中的某个节点移到末尾，所以定义一个方法
    def move_node_to_tail(self, key):
            # 先将哈希表key指向的节点拎出来，为了简洁起名node
            #      hashmap[key]                               hashmap[key]
            #           |                                          |
            #           V              -->                         V
            # prev <-> node <-> next         pre <-> next   ...   node
            node = self.hashmap[key]
            node.prev.next = node.next
            node.next.prev = node.prev
            # 之后将node插入到尾节点前
            #                 hashmap[key]                 hashmap[key]
            #                      |                            |
            #                      V        -->                 V
            # prev <-> tail  ...  node                prev <-> node <-> tail
            node.prev = self.tail.prev
            node.next = self.tail
            self.tail.prev.next = node
            self.tail.prev = node

    def get(self, key):
        if key in self.hashmap:
            # 如果已经在链表中了久把它移到末尾（变成最新访问的）
            self.move_node_to_tail(key)
        res = self.hashmap.get(key, -1)
        if res == -1:
            return res
        else:
            return res.value

    def put(self, key, value):
        if key in self.hashmap:
            # 如果key本身已经在哈希表中了就不需要在链表中加入新的节点
            # 但是需要更新字典该值对应节点的value
            self.hashmap[key].value = value
            # 之后将该节点移到末尾
            self.move_node_to_tail(key)
        else:
            if len(self.hashmap) == self.capacity:
                # 去掉哈希表对应项
                self.hashmap.pop(self.head.next.key)
                # 去掉最久没有被访问过的节点，即头节点之后的节点
                self.head.next = self.head.next.next
                self.head.next.prev = self.head
            # 如果不在的话就插入到尾节点前
            new = ListNode(key, value)
            self.hashmap[key] = new
            new.prev = self.tail.prev
            new.next = self.tail
            self.tail.prev.next = new
            self.tail.prev = new

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

15、前缀和

leetcode5248. 统计「优美子数组」

给你一个整数数组 nums 和一个整数 k。

如果某个子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。

请返回这个数组中「优美子数组」的数目。

思路1：前缀和+hashmap

• 先求取nums中奇数个数的前缀和arr，即arr[i]表示nums数组中前ii个数有多少个奇数。
• 则对于每一个子数组nums[i…j]，其中的奇数个数可以采用arr[j]-arr[i-1]求得
• 则问题转换成有多少个数对(i,j)(i,j)，其中arr[j]-arr[i] =
  k，这就是我们喜闻乐见的two sum问题啦，用hashhash表即可O(n)解决

作者：aleix
链接：https://leetcode-cn.com/problems/count-number-of-nice-subarrays/solution/qian-zhui-he-hash-jian-dan-yi-li-jie-by-aleix/

from collections import defaultdict
class Solution:
    def numberOfSubarrays(self, nums: list, k: int) -> int:
        qz_sum=[0]
        for i in range(len(nums)):
            qz_sum.append(qz_sum[-1]+(nums[i]&1))

        hashmap=defaultdict(int)
        ret=0
        for i in range(len(qz_sum)):
            ret+=hashmap[qz_sum[i]-k]
            hashmap[qz_sum[i]]+=1
        return ret
1
2
3
4
5
6
7
8
9
10
11
12
13

思路2：直接计算

class Solution:
    def numberOfSubarrays(self, nums: List[int], k: int) -> int:
        jishu=[0]
        # nums=[1]+nums[:]+[1]
        for i in range(len(nums)):
            if nums[i]&1:
                jishu.append(i+1)
        jishu.append(i+2)
        lt,rt=1,1
        idx=0
        l=len(jishu)
        cnt=[]
        while idx+k<=l:
            if idx!=0:
                lt=jishu[idx]-jishu[idx-1]
            else:
                lt=1
            if idx+k!=l:
                rt=jishu[idx+k]-jishu[idx+k-1]
            else:
                rt=1
            
            cnt.append(rt*lt)
            idx+=1
        return sum(cnt[1:-1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

17.基础数据数据结构实现特定数据结构

面试题09. 用两个栈实现队列

函数设计：
题目只要求实现 加入队尾appendTail() 和 删除队首deleteHead() 两个函数的正常工作，因此我们可以设计栈 A 用于加入队尾操作，栈 B 用于将元素倒序，从而实现删除队首元素。

加入队尾 appendTail()函数： 将数字 val 加入栈 A 即可。
删除队首deleteHead()函数： 有以下三种情况。

1. 当栈 B 不为空： B中仍有已完成倒序的元素，因此直接返回 B 的栈顶元素。
2. 否则，当 A 为空： 即两个栈都为空，无元素，因此返回-1 。
3. 否则： 将栈 A 元素全部转移至栈 B 中，实现元素倒序，并返回栈 B 的栈顶元素。

class CQueue:
    def __init__(self):
        self.stack1 = []
        self.stack2 = []

    def appendTail(self, value: int) -> None:
        self.stack1.append(value)
        
    def deleteHead(self) -> int:
        if not self.stack1 and not self.stack2:
            return -1
        if self.stack2:
            return self.stack2.pop()
        while self.stack1:
            self.stack2.append(self.stack1.pop())
        return self.stack2.pop()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

leetcode716. 最大(小)栈

设计一个最大栈，支持 push、pop、top、peekMax 和 popMax 操作。

push(x) – 将元素 x 压入栈中。
pop() – 移除栈顶元素并返回这个值。
top() – 返回栈顶元素。
peekMax() – 返回栈中最大元素。
popMax() – 返回栈中最大的元素，并将其删除。如果有多个最大元素，只要删除最靠近栈顶的那个。
思路

1. 初始化两个栈：一个数据栈，一个维护最大值得栈
2. push操作：数据栈直接入栈，最大栈如栈顶与当前值的最大值
3. pop:数据栈和最大栈直接出栈
4. peekmax():返回最大栈的栈顶
5. popmax()：一直出栈查找最大值，将出战的数据缓存在另一个栈中 ，删除最大值后在将数据返还

class MaxStack {
    Stack<Integer> stack;
    Stack<Integer> maxStack;

    public MaxStack() {
        stack = new Stack();
        maxStack = new Stack();
    }

    public void push(int x) {
        int max = maxStack.isEmpty() ? x : maxStack.peek();
        maxStack.push(max > x ? max : x);
        stack.push(x);
    }

    public int pop() {
        maxStack.pop();
        return stack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int peekMax() {
        return maxStack.peek();
    }

    public int popMax() {
        int max = peekMax();
        Stack<Integer> buffer = new Stack();
        while (top() != max) buffer.push(pop());
        pop();
        while (!buffer.isEmpty()) push(buffer.pop());
        return max;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

1x、其他说不清的神奇代码

leetcode周赛151，5164. 从链表中删去总和值为零的连续节点

给你一个链表的头节点 head，请你编写代码，反复删去链表中由 总和 值为 0 的连续节点组成的序列，直到不存在这样的序列为止。

删除完毕后，请你返回最终结果链表的头节点。
输入：head = [1,2,-3,3,1]
输出：[3,1]
提示：答案 [1,2,1] 也是正确的。

思路：

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

def to_list(h):
    ans = []
    while h:
        ans.append(h.val)
        h = h.next
    return ans


def to_link(l):
    n = ListNode(None)
    h = n
    for node in l:
        n.next = ListNode(node)
        n = n.next
    return h.next


class Solution(object):
    def removeZeroSumSublists(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        l = to_list(head)
        ans = list()
        for n in l:
            ans.append(n)
            s = 0
            for k in reversed(xrange(len(ans))):
                s += ans[k]
                if s == 0:
                    ans = ans[:k]
                    break
        return to_link(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40