运筹说 第60期 | 0-1型整数规划和指派问题_0-1整数规划

通过前两期的学习，我们已经学会了整数规划问题的数学模型、割平面法和分支定界法。本期小编带大家学习0-1整数问题和指派问题。

 

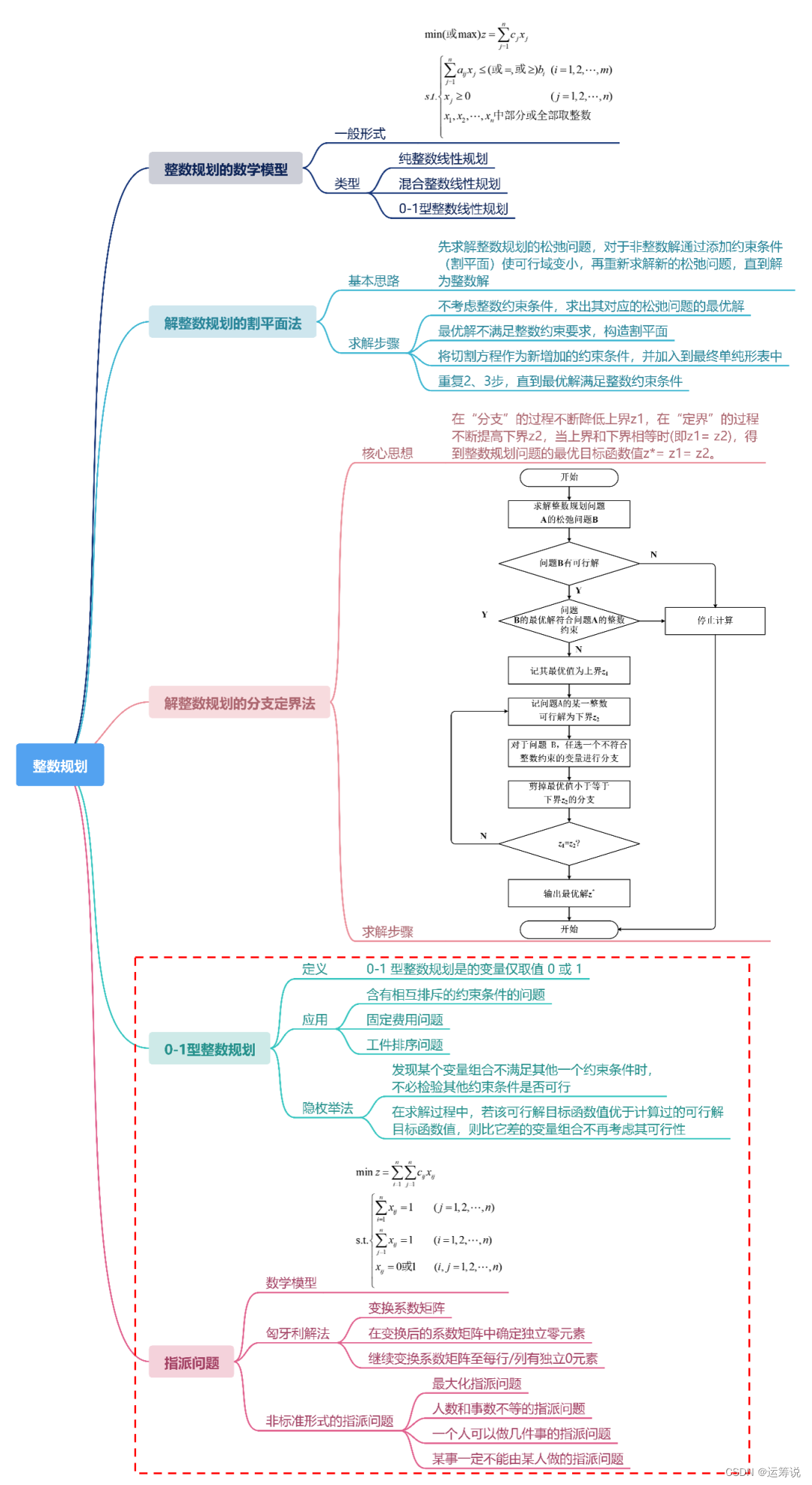
一 0-1整数规划

01定义

0-1型整数规划是整数规划的一种特殊形式，它的变量xj仅取值0或1。这种只能取0或1的变量称为0-1变量或二进制变量。例如

当问题含有多项限制要素E1,E2,…,En，其中每项都有两种选择时，可令

若遇到变量可以取多个整数值时，可以用一组0-1变量取代该变量。例如，变量x可取0与9之间的任意整数时，可令

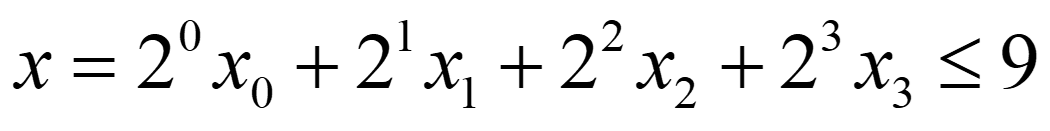
其中，x0，x1，x2，x3皆为0-1变量。

02应用

案例1 含有互斥约束条件的问题 

案例2 固定费用问题  

案例3 工件排序问题 

 

03解法

对于0-1型整数规划，一般采用隐枚举法，而不必采用完全枚举法：

1、只要发现某个变量组合不满足其中一个约束条件时，就不必再去检验其他约束条件是否可行。

2、若已发现一个可行解，则可根据它的目标函数值产生一个过滤条件，对于目标函数值比它差的变量组合就不必再去检验它的可行性；在以后的求解中，每当发现更好的可行解，则以此替换原来的过滤条件。

案例4 

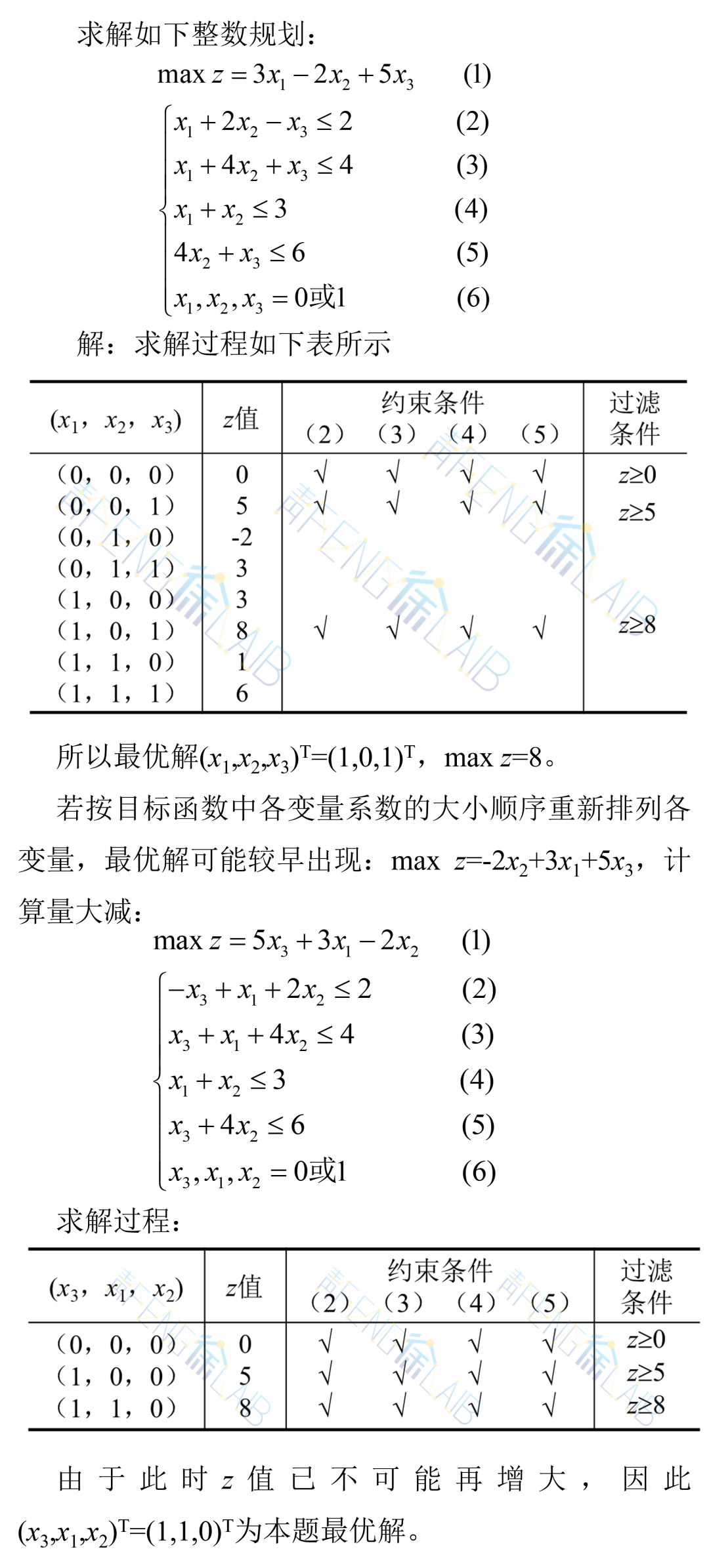
二 指派问题

01数学模型

02 匈牙利解法

1955年，库恩利用匈牙利数学家康尼格的关于矩阵中独立零元素的定理，提出了解指派问题的一种算法，称为匈牙利解法。

 ★核心思想

 若从指派问题的系数矩阵C的某行（或某列）各元素分别减去一个常数k，得到一个新的矩阵C’，则以C’和C为系数矩阵的两个指派问题有相同的最优解。这是由于系数矩阵的变化并不影响数学模型的约束方程组，只是目标函数值减少了常数k，所以最优解不变。

★ 匈牙利解法步骤

1、变换系数矩阵，先对各行元素分别减去本行中的最小元素，再对各列元素分别减去本列最小元素，从而保证系数矩阵中每行及每列中至少有一个零元素。

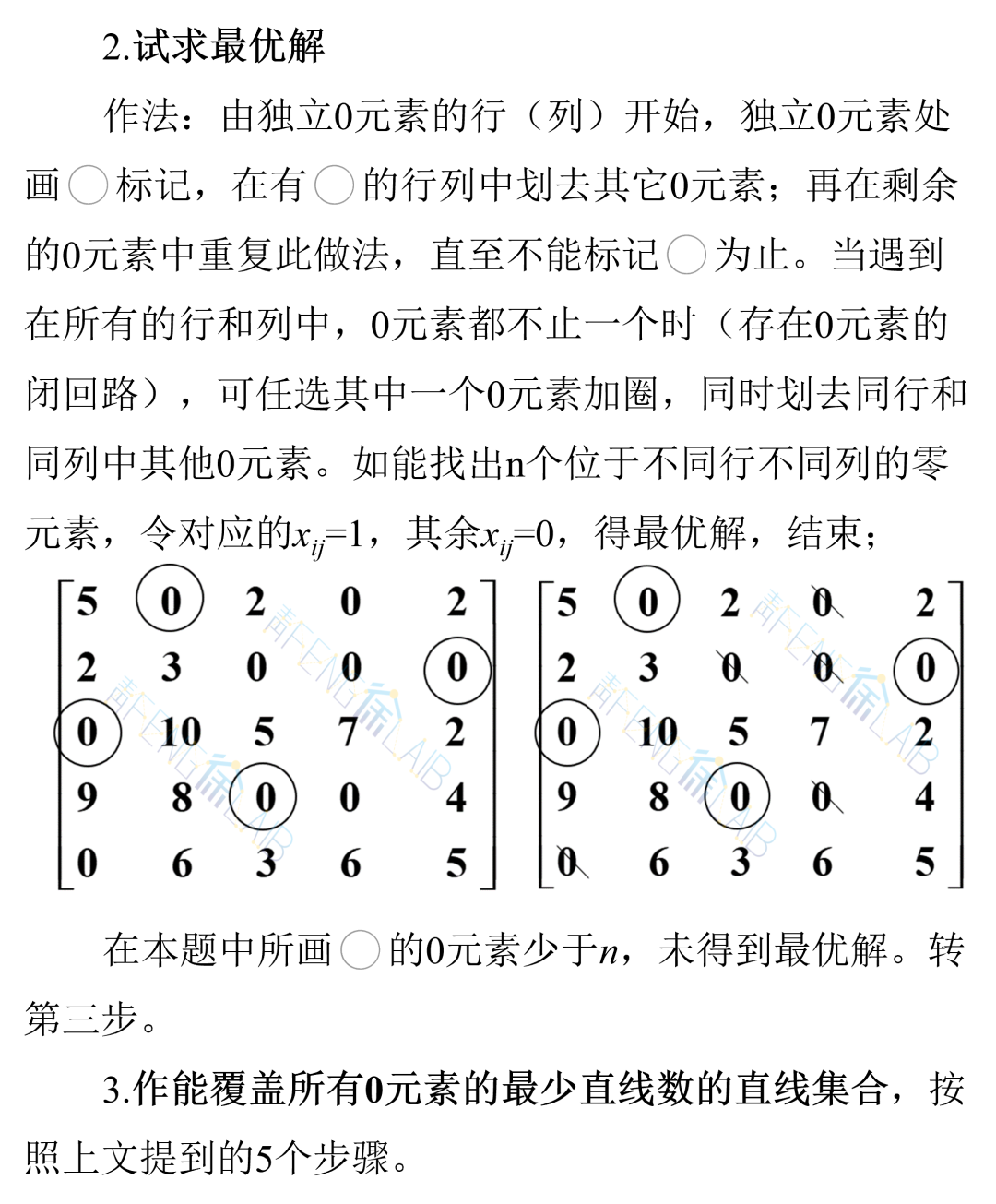
2、在变换后的系数矩阵中确定独立零元素。若独立零元素有n个，则已得出最优解；若独立零元素少于n个，则做能覆盖所有零元素的最少直线数目的直线集合。

（1）对没有⚪的行打√号；

（2）对已打√号的行中所有被划去0元素的所在列打√号；

（3）再对打有√号的列中⚪中0元素的所在行打√号；

（4）重复(2)(3)，直到得不出新的打√号的行(列)为止；

（5）对没有打√号的行画横线，对打√号的列画一纵线，这就得到覆盖所有0元素的最少直线数目的直线集合。

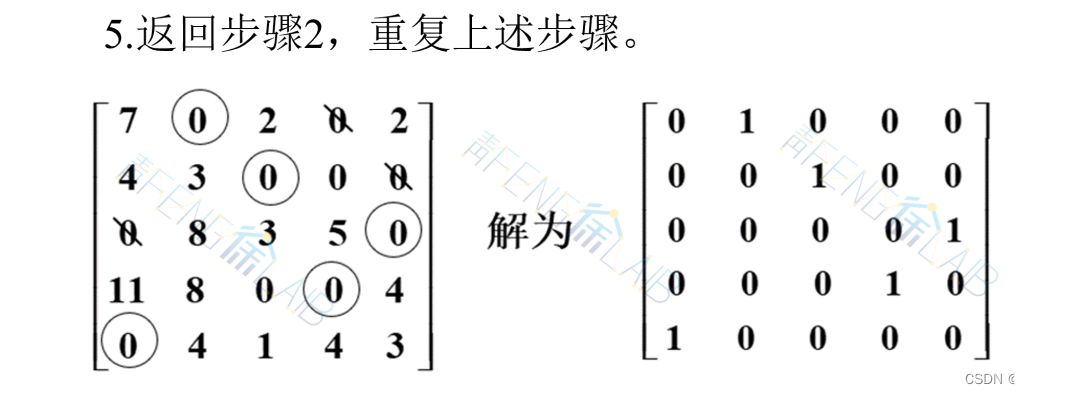
3、继续变换系数矩阵，在未被直线覆盖的元素中找出一个最小元素，对未被覆盖的元素所在行（或列）中各元素都减去这一最小元素。对出现负元素的行或列都加上这一最小元素。返回步骤2。

案例5 

求表中所示效率矩阵的指派问题的最小解

 

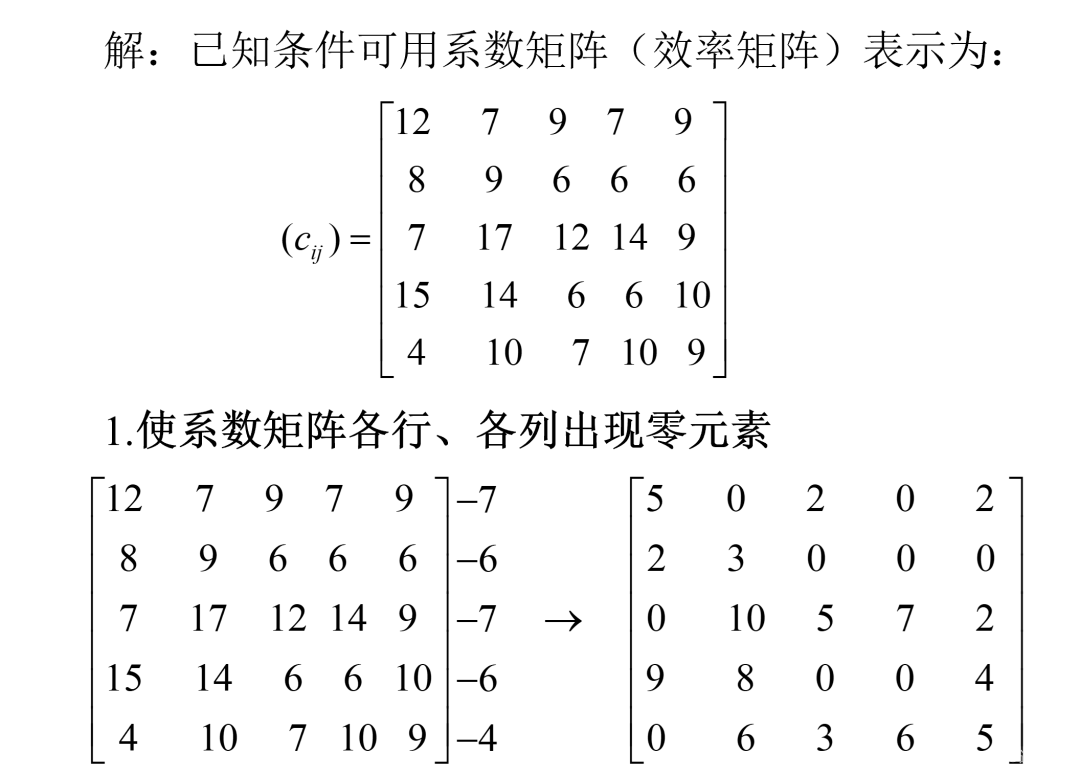
03 非标准形式的指派问题

核心思想

对于非标准形式的指派问题，通常的处理方法是先将它们转化为标准形式然后求解。

★最大化指派问题

当面对最大化指派问题，可以从系数矩阵C中，找出最大元素m，用m减去矩阵C中所有元素得到系数矩阵B，则以B为系数矩阵的最小化指派问题和以C为系数矩阵的原最大化指派问题有相同最优解。

★ 人数和事数不等的指派问题

若人数少事件多，添上虚拟的人，费用系数值为0。

若事件少人数多，添上虚拟的事件，费用系数值为0。

★ 一个人可做几件事的指派问题

将该人化作相同的几个人来接受指派，这几个人做同一事件的费用系数都一样。

★ 某事一定不能由某人做的指派问题

若某事一定不能由某人做，将相应的费用系数取作足够大的数M。

以上就是关于0-1整数规划和指派问题的全部内容了，学习完这一节，大家可以试着对一些实际问题进行应用练习。下一次小编将带大家学习第六章——非线性规划，敬请关注！   

---

作者 | 陈优 王连聚

责编 | 刘文志

审核 | 徐小峰