【全网最全】2024深圳杯数学建模ABCD题参考论文【附带每小问完整解题代码+最终结果】_2024深圳杯a题参考论文.pdf

每个题对应的全套资料都在下文对应题目的标题下面，目前ABCD四个题已经全部更新完毕拉！

一 问题重述

1.1 问题背景

当今，火箭技术已经成为太空探索和卫星发射等领域的核心。绝大多数火箭都采用多 级火箭结构，其中下面级火箭或助推器在完成既定任务后会分离并坠落至地面。然而，在 坠落过程中，火箭残骸会产生跨音速音爆，这不仅会对周围环境造成一定程度的干扰，还 会给火箭残骸的回收带来极大的挑战。

为了快速、精准地回收火箭残骸，一种创新的方法被提出：在残骸的理论落区内布置 多台震动波监测设备。这些设备能够接收到不同火箭残骸在空中产生的跨音速音爆，并根 据音爆抵达的时间来定位空中残骸发生音爆时的位置。通过采用弹道外推技术，研究人员 可以快速而准确地确定火箭残骸的落地点，为后续的回收工作提供了重要的支持。

这项技术的提出和应用将极大地提高火箭残骸回收的效率和精度，有望为未来的太空 探索和卫星发射等活动提供更加可靠的支持。

1.2 问题重述

问题 1:建立数学模型，分析如果要精准确定空中单个残骸发生音爆时的位置坐标（经 度、纬度、高程）和时间，至少需要布置几台监测设备？假设某火箭一级残骸分离后，在 落点附近布置了 7 台监测设备，各台设备三维坐标（经度、纬度、高程）、音爆抵达时间 （相对于观测系统时钟 0 时）, 计算残骸发生音爆时的位置和时间。

问题 2:火箭残骸除了一级残骸，还有两个或者四个助推器。在多个残骸发生音爆时， 监测设备在监测范围内可能会采集到几组音爆数据。假设空中有 4 个残骸，每个设备按照 时间先后顺序收到 4 组震动波。建立数学模型，分析如何确定监测设备接收到的震动波是 来自哪一个残骸？如果要确定 4 个残骸在空中发生音爆时的位置和时间，至少需要布置多 少台监测设备？

问题 3:假设各台监测设备布置的坐标和 4 个音爆抵达时间. 利用问题 2 所建立的数学模 型，从上表中选取合适的数据，确定 4 个残骸在空中发生音爆时的位置和时间（4 个残骸  产生音爆的时间可能不同，但互相差别不超过 5 s）。

问题 4:假设设备记录时间存在 0.5 s 的随机误差，请修正问题 2 所建立的模型以较精   确地确定 4 个残骸在空中发生音爆时的位置和时间。通过对问题 3 表中数据叠加随机误差， 给出修正模型的算例，并分析结果误差。如果时间误差无法降低，提供一种解决方案实现  残骸空中的精准定位（误差< 1 km），并自行根据问题 3 所计算得到的定位结果模拟所需  的监测设备位置和音爆抵达时间数据，验证相关模型。

B题批量工件并行切割下料优化研究

【无水印word】2024深圳杯B题成品论文43页（附带1-4小问完整py解题代码思路）https://www.jdmm.cc/file/2710664

43页成品论文：

本研究针对批量工件并行切割下料问题展开了深入的探讨与分析。通过建立数学模型和运用优化算法，我们旨在最大化板材面积利用率、最小化切割下料时间，并考虑能量、板材和设备时间的经济价值。符号说明部分详细解释了各种符号的含义和单位，涵盖了影响问题解决的关键因素。在面对不同题目时，我们采用了多种优化模型，如几何优化模型、动态规划、多目标规划等，以解决实际生产中的复杂挑战。本研究的结论对于提高生产效率、降低成本、优化资源利用具有重要的参考意义。通过整合理论分析和实践操作，我们为批量工件下料问题的解决提供了新的思路和方法。

第一题： 针对三种矩形板材 A80002500、B60002000、C6000*2500 和附件1中的工件模板，我们设计了切割排版方案以极大化板材面积利用率，并确保每块板材切割出的工件至少包含5种型号。通过建立数学模型和优化算法，实现了高效的切割下料方案。

第二题： 在最多使用5把切割刀的限制下，针对A、B、C 三种型号板材进行工件切割，以最小化整块板的切割下料所需时间为目标。优化设计了轨道一维移动和切割刀具的协同运行方案，有效降低了生产时间成本。

第三题： 结合附件2给出的批量工件型号分布，我们选取不同数量组合的 A、B、C 型板材进行切割下料，以极大化三种型号板材的总体面积利用率为目标。通过精心设计的切割排版方案，实现了资源的最大化利用。

第四题： 在考虑总体利用率约束的基础上，利用最多10把切割刀进行批量工件切割，以极小化总体切割下料所需时间为目标。通过优化每个型号板材数量和切割排版方案，平衡了资源利用和生产效率要求。

第五题： 最终考虑能量、板材和设备时间的经济价值，使用最多10把刀具进行批量工件的切割下料，并极小化使用的能量、板材和设备时间的综合成本。在此基础上，还要考虑到各成本因素的价格比例，以及维持至少与第三问中排版利用率的95%。

关键词：批量工件下料；并行切割；利用率最大化；动态规划；目标优化。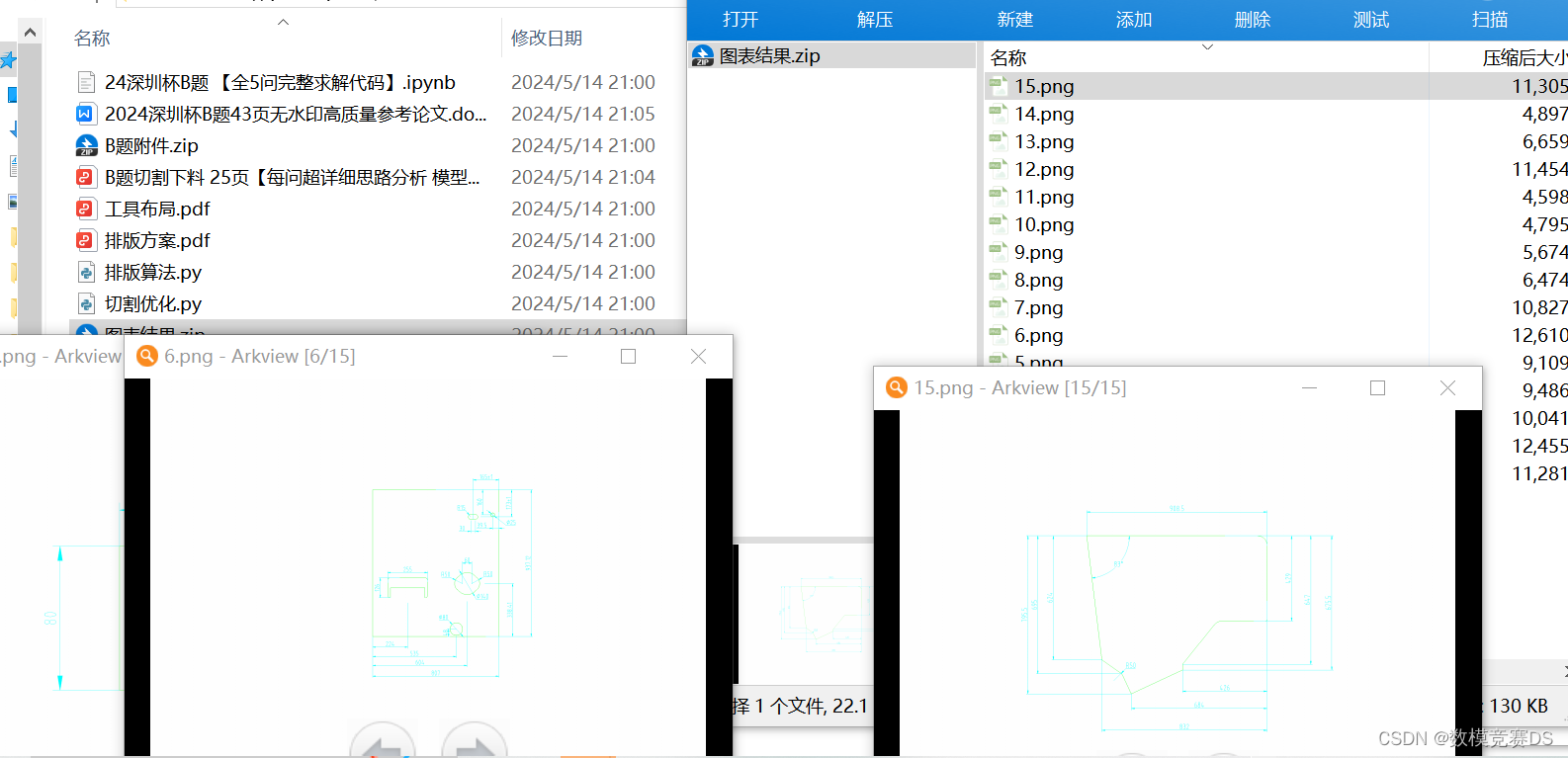

       2024深圳杯数学建模C题编译器识别问题

【编译器识别】2024深圳杯C题24页参考论文+1-3小问完整解题代码https://www.jdmm.cc/file/2710545/

24页参考论文更新

一、问题研究

为了回答这些问题，我们需要进行一系列的编译实验、分析编译结果，并构建判别函数。以下是对这些问题的初步分析和可能的方法：

问题1：编译并对比结果

1.获取不同版本的GCC编译器：首先，需要确保安装了不同版本的GCC编译器。这可以通过下载和安装不同版本的GCC或使用包管理器（如apt, yum等）来实现。

2.编译附件1中的程序：使用每个版本的GCC编译器编译附件1中的C++源代码，并确保使用默认编译选项（通常是不带任何额外标志的g++命令）。

3.对比编译结果：对比不同版本编译器生成的编译输出（包括警告、错误和生成的代码）以及二进制文件。寻找明显的不同点，比如特定的警告信息、优化级别或生成的机器码差异。

问题2：构建判别函数

1.提取特征：从编译结果中提取关键特征，如特定警告信息、编译器的内建版本信息字符串等。

2.设计判别逻辑：根据提取的特征，设计判别逻辑。这可能是一个简单的if-else结构，或者是基于规则的匹配系统，甚至是机器学习模型。

3.验证判别函数：使用已知版本的GCC编译器生成的编译结果来验证判别函数的准确性。

问题3：应用判别函数

1.编译附件2中的程序：使用不同版本的GCC编译器编译附件2中的C++源代码，并收集编译结果。

2.应用判别函数：将问题2中构建的判别函数应用于附件2的编译结果，观察其是否能够正确区分不同版本的编译器。

3.研究泛化性：比较附件1和附件2的代码，分析哪些编译结果特征是通用的，哪些是特定于某个代码的。这有助于提高判别函数的泛化性。

问题4：提高判别函数性能的建议

1.增加特征：考虑从编译输出中提取更多特征，如编译时间、生成文件的大小等。

2.使用机器学习：考虑使用机器学习算法来训练一个分类器，根据编译结果自动区分编译器版本。

D题基于有限元分析的音板振动模态分析与参数识别

2024深圳杯D题42页成品论文+1-4小问完整代码+高清结果图https://www.jdmm.cc/file/2710609

一等奖42页高质量参考论文

摘  要

本文针对音板振动建模与参数识别的一系列问题,采用了多种数学建模方法和求解算法,对相关问题进行了深入分析和求解。问题1的 Kirchhoff-Love 均质薄板振动模型：我们首先建立了基于Kirchhoff-Love薄板理论的均质薄板振动模型,该模型采用了垂直于中面的直线保持直线、厚度保持不变、法向应力可忽略不计等假设。在此基础上,我们得到了描述薄板自由振动的偏微分方程组。对于具有自由边界条件的方形薄板,我们还建立了相应的边界条件方程。为了求解该振动模型,我们采用了Ritz方法。

问题2的非均质薄板振动模型： 针对问题2,我们在Kirchhoff-Love理论的基础上,进一步建立了考虑几何非均匀性的非均质薄板振动模型。该模型引入了位置相关的材料参数(密度、弹性模量、泊松比)和几何参数(厚度、弯曲角),以更准确地描述薄板的振动行为。为了求解非均质薄板振动模型,我们提出了基于分片多项式插值的算法。具体来说,我们将整个平面区域划分为若干单元,在每个单元内采用多项式函数对厚度和弯曲角分布进行拟合。最后采用Ritz法或Galerkin法求解。

问题3的分离变量法振动模型：针对问题3给出的非均质音板振动信息,我们建立了基于分离变量法的振动模型。该模型将音板的振动位移表示为时间函数和空间振型函数的乘积形式,大大简化了问题的复杂性。为了描述附件提供的5个振型函数$\varphi_j(x,y)$,我们采用了傅里叶级数展开的方法。

问题4的参数识别模型：针对问题4,我们建立了基于非均质音板振动理论的参数识别模型。该模型将密度、杨氏模量、泊松比和厚度等位置相关参数作为待识别对象,目标是确定满足给定振型信息的参数分布。

通过合理选择和扩展这些模型,我们不仅能够有效地求解音板振动问题,还可以深入理解影响振动行为的关键因素,为实际音乐乐器的设计和制造提供重要参考。

关键词：Kirchhoff-Love理论； 振动模型；Ritz 法求解算法； 频率； 音板

配套代码数据：

解题步骤：

（1）定义参数：定义了正方形板的几何尺寸、材料属性等参数。

（2）计算材料属性：根据输入的材料参数，计算出材料属性矩阵D，这个矩阵描述了材料的弹性特性。

（3）创建网格：创建了一个二维网格，用于表示正方形板的几何形状。

（4）组装刚度矩阵和质量矩阵：通过遍历网格的每个单元，计算每个单元的刚度矩阵和质量矩阵，然后将它们组装成整体的刚度矩阵K和质量矩阵M。

（5）求解广义特征值问题：使用eigs函数求解广义特征值问题，得到模态振动的频率和振动模态。

（6）绘制模态形状：通过遍历每个振动模态，将其在二维网格上进行插值并绘制出来，从而可视化每个振动模态的形状。

圆形音板相关分析结果：