机器学习数据获取与处理_机器学习的数据怎么得到啊

数据获取与处理（以CV任务为主）

• 课程目的

1. 数据的获取途径
2. 数据处理与标注
3. 数据预处理方法
4. 模型训练评估

一、数据集的获取

  通常，我们的数据来源于各个比赛平台。首先是AIStudio中的数据集，大部分经典数据集例如百度AI Studio ,Kaggle、天池、讯飞等平台（通过关键词搜索获取需要的数据集），或者是Github。还有一些小的平台，需要大家自己去看。通常来说，数据集用于学术目的，有些数据需要申请才能获得链接。

1.1 Kaggle有趣比较火热的数据集

House Prices-Advanced Regression Techniques       预测销售价格

Cat and Dog                         猫狗分类

Machine Learning from Disaster      预测泰坦尼克号的生存情况并熟悉机器学习基础知识

1.2 天池

Barley Remote Sensing Dataset大麦遥感检测数据集     遥感影像分割

耶鲁人脸数据库                   目标检测任务(人脸检测)

1.3 DataFountain

花卉分类数据集                       图像分类

1.4 其他常用的数据集官网

科大讯飞官网

COCO数据集

1.5 完整流程概述

1.5.1 图像处理完整流程

• 1. 图片数据获取
• 1. 图片数据清洗

  ----初步了解数据，筛选掉不合适的图片

• 1. 图片数据标注
• 1. 图片数据预处理data preprocessing。

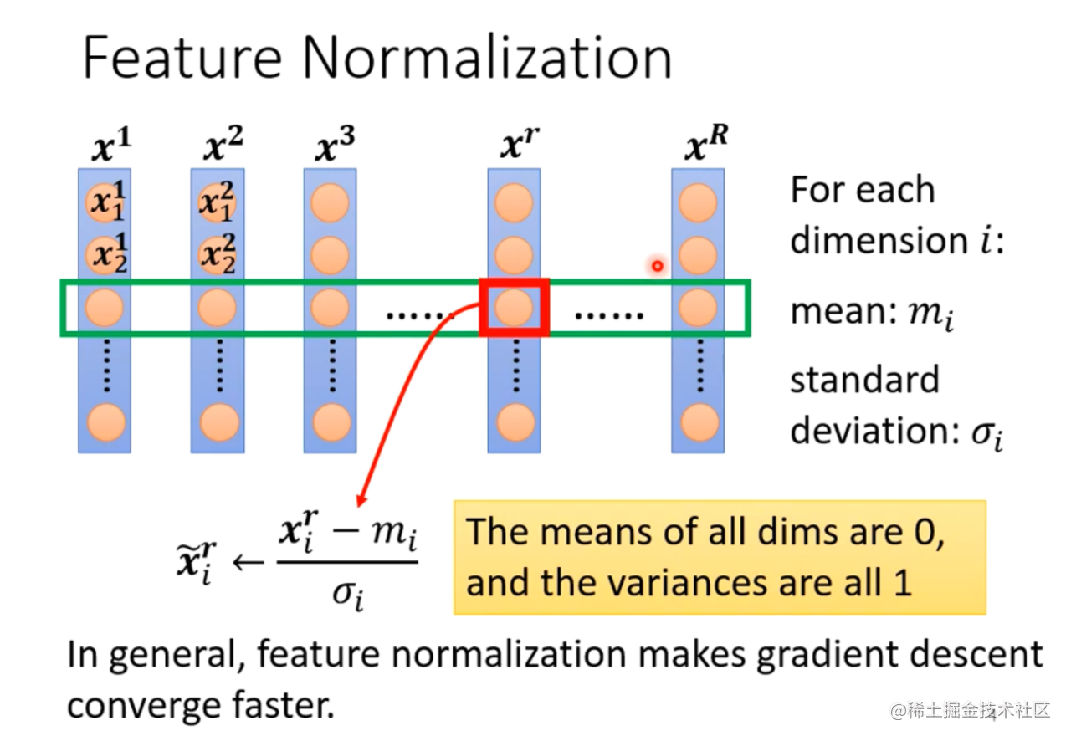
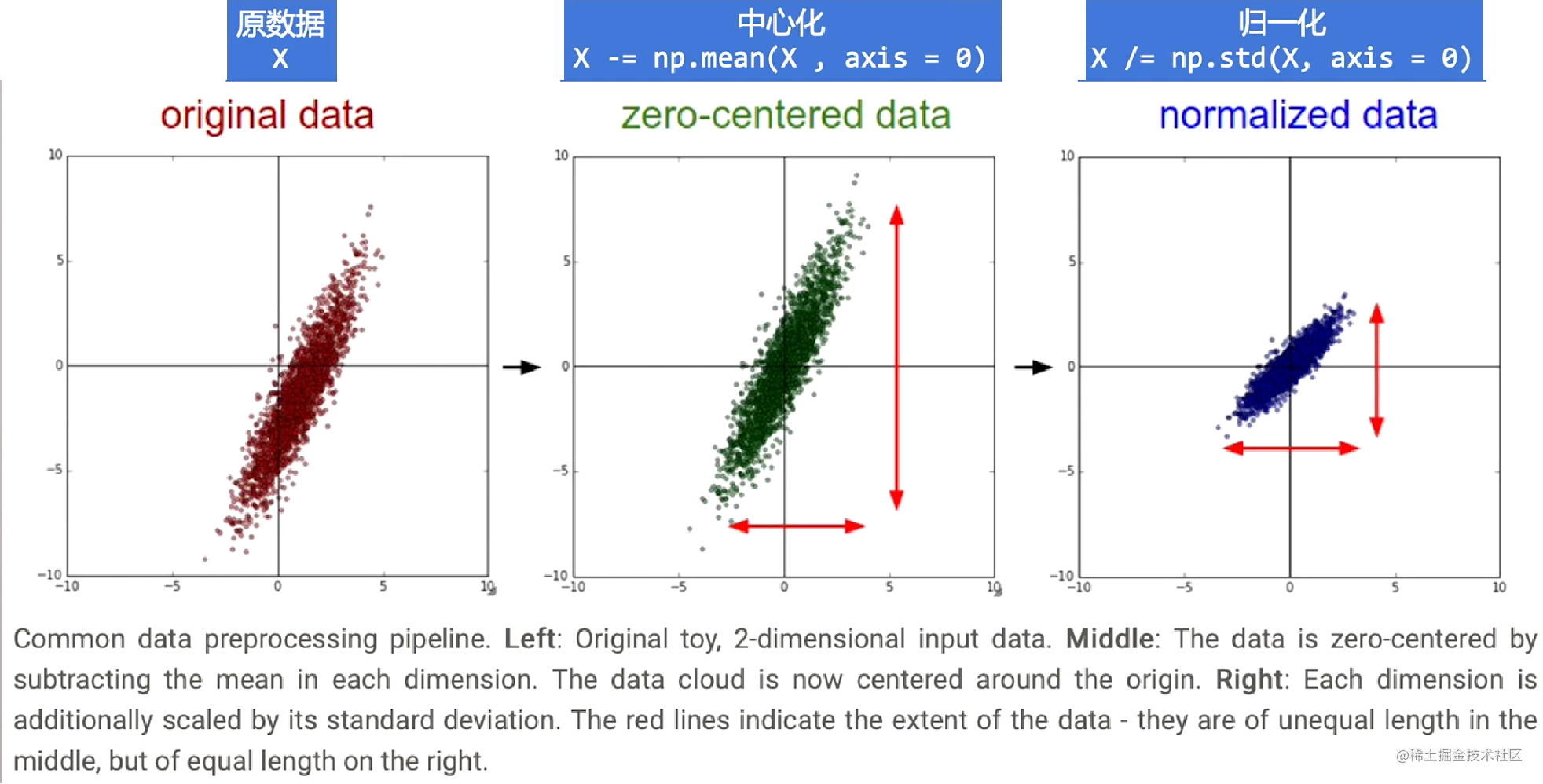
  ----标准化 standardlization

    一 中心化 = 去均值 mean normallization

      一 将各个维度中心化到0

      一 目的是加快收敛速度,在某些激活函数上表现更好

     一 归一化 = 除以标准差

      一 将各个维度的方差标准化处于[-1,1]之间

      一 目的是提高收敛效率,统一不同输入范围的数据对于模型学习的影响,映射到激活函数有效梯度的值域

• 1. 图片数据准备data preparation(训练+测试阶段)

  ----划分训练集，验证集，以及测试集

• 1. 图片数据增强data augjmentation（训练阶段 ）

  ----CV常见的数据增强

       · 随机旋转

       · 随机水平或者重直翻转

       · 缩放

       · 剪裁

       · 平移

       · 调整亮度、对比度、饱和度、色差等等

       · 注入噪声

       · 基于生成对抗网络GAN做数搪增强AutoAugment等

1.5.2 纯数据处理完整流程

• 数据预处理与特征工程

• 1.感知数据

  ----初步了解数据

  ----记录和特征的数量特征的名称

  ----抽样了解记录中的数值特点描述性统计结果

  ----特征类型

  ----与相关知识领域数据结合，特征融合

• 2.数据清理

  ----转换数据类型

  ----处理缺失数据

  ----处理离群数据

• 3.特征变换

  ----特征数值化

  ----特征二值化

  ----OneHot编码

  ----特征离散化特征

  ----规范化

    区间变换

    标准化

    归一化

• 4.特征选择

  ----封装器法

    循序特征选择

    穷举特征选择

    递归特征选择

  ----过滤器法

  ----嵌入法

• 5.特征抽取

  ----无监督特征抽取

    主成分分析

    因子分析

  ----有监督特征抽取

拓展小知识:

   皮尔森相关系数是用来反应俩变量之间相似程度的统计量，在机器学习中可以用来计算特征与类别间的相似度，即可判断所提取到的特征和类别是正相关、负相关还是没有相关程度。 Pearson系数的取值范围为[-1,1]，当值为负时，为负相关，当值为正时，为正相关，绝对值越大，则正/负相关的程度越大。若数据无重复值，且两个变量完全单调相关时，spearman相关系数为+1或-1。当两个变量独立时相关系统为0，但反之不成立。

用Corr()函数即可，(保证行相同)。

公式如下:

ρX,Y=cov⁡(X,Y)σXσY=E((X−μX)(Y−μY))σXσY=E(XY)−E(X)E(Y)E(X2)−E2(X)E(Y2)−E2(Y)\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{X} \sigma_{Y}}=\frac{E\left(\left(X-\mu_{X}\right)\left(Y-\mu_{Y}\right)\right)}{\sigma_{X} \sigma_{Y}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{E\left(X^{2}\right)-E^{2}(X)} \sqrt{E\left(Y^{2}\right)-E^{2}(Y)}}ρX,Y​=σX​σY​cov(X,Y)​=σX​σY​E((X−μX​)(Y−μY​))​=E(X2)−E2(X)​E(Y2)−E2(Y)​E(XY)−E(X)E(Y)​

当两个变量的标准差都不为零时，相关系数才有定义，Pearson相关系数适用于：

(1)、两个变量之间是线性关系，都是连续数据。

(2)、两个变量的总体是正态分布，或接近正态的单峰分布。</