自然语言处理应用(二)：自然语言推断_contradiction nlp

自然语言推断

自然语言推断（Natural Language Inference）是指通过对自然语言文本进行逻辑推理和推断，判断两个句子之间的关系，通常包括三种关系：蕴含（entailment）、矛盾（contradiction）和中性（neutral）。

在自然语言推断任务中，通常给出一个前提（premise）和一个假设（hypothesis），需要根据前提和假设之间的关系来判断前提是否蕴含、矛盾或中性地支持假设。例如：

前提：狗在玩球。
假设：有一只动物正在玩耍。

在这个例子中，前提和假设之间存在蕴含关系，因为前提表明狗正在玩球，而假设中提到有一只动物正在玩耍，这两个句子的意思是相同的。

自然语言推断是自然语言处理和人工智能领域中一个重要的任务，对于理解和处理自然语言具有重要意义。它在很多应用中都有广泛的应用，例如问答系统、机器翻译、信息检索等。

为了解决自然语言推断问题，研究者们通常使用机器学习和深度学习方法，构建模型来自动进行推断。这些模型会通过学习大规模的标注数据集，使其具备推断能力，并能够泛化到未见过的句子对上。

常见的自然语言推断模型包括基于逻辑回归、支持向量机（SVM）、决策树等传统机器学习方法，以及基于神经网络的模型，如循环神经网络（RNN）、长短时记忆网络（LSTM）、Transformer等。

文章内容来自李沐大神的《动手学深度学习》并加以我的理解，感兴趣可以去https://zh-v2.d2l.ai/查看完整书籍

---

---

自然语言处理

自然语言推断（natural language inference）主要研究 假设（hypothesis）是否可以从前提（premise）中推断出来， 其中两者都是文本序列。 换言之，自然语言推断决定了一对文本序列之间的逻辑关系。这类关系通常分为三种类型：

1. 蕴涵（entailment）：假设可以从前提中推断出来。

2. 矛盾（contradiction）：假设的否定可以从前提中推断出来。

3. 中性（neutral）：所有其他情况。

自然语言推断也被称为识别文本蕴涵任务。 例如，下面的一个文本对将被贴上“蕴涵”的标签，因为假设中的“表白”可以从前提中的“拥抱”中推断出来。

前提：两个女人拥抱在一起。
假设：两个女人在示爱。

下面是一个“矛盾”的例子，因为“运行编码示例”表示“不睡觉”，而不是“睡觉”。

前提：一名男子正在运行Dive Into Deep Learning的编码示例。
假设：该男子正在睡觉。

第三个例子显示了一种“中性”关系，因为“正在为我们表演”这一事实无法推断出“出名”或“不出名”。

前提：音乐家们正在为我们表演。
假设：音乐家很有名。

自然语言推断一直是理解自然语言的中心话题。它有着广泛的应用，从信息检索到开放领域的问答。为了研究这个问题，我们将首先研究一个流行的自然语言推断基准数据集。

斯坦福自然语言推断（SNLI）数据集

斯坦福自然语言推断语料库（Stanford Natural Language Inference，SNLI）是由500000多个带标签的英语句子对组成的集合 (Bowman et al., 2015)。我们在路径…/data/snli_1.0中下载并存储提取的SNLI数据集。

import os
import re
import torch
from torch import nn
from d2l import torch as d2l

#@save
d2l.DATA_HUB['SNLI'] = (
    'https://nlp.stanford.edu/projects/snli/snli_1.0.zip',
    '9fcde07509c7e87ec61c640c1b2753d9041758e4')

data_dir = d2l.download_extract('SNLI')
1
2
3
4
5
6
7
8
9
10
11
12

读取数据集

原始的SNLI数据集包含的信息比我们在实验中真正需要的信息丰富得多。因此，我们定义函数read_snli以仅提取数据集的一部分，然后返回前提、假设及其标签的列表。

#@save
def read_snli(data_dir, is_train):
    """将SNLI数据集解析为前提、假设和标签"""
    def extract_text(s):
        # 删除我们不会使用的信息
        s = re.sub('\\(', '', s)
        s = re.sub('\\)', '', s)
        # 用一个空格替换两个或多个连续的空格
        s = re.sub('\\s{2,}', ' ', s)
        return s.strip()
    label_set = {'entailment': 0, 'contradiction': 1, 'neutral': 2}
    file_name = os.path.join(data_dir, 'snli_1.0_train.txt'
                             if is_train else 'snli_1.0_test.txt')
    with open(file_name, 'r') as f:
        rows = [row.split('\t') for row in f.readlines()[1:]]
    premises = [extract_text(row[1]) for row in rows if row[0] in label_set]
    hypotheses = [extract_text(row[2]) for row in rows if row[0] \
                in label_set]
    labels = [label_set[row[0]] for row in rows if row[0] in label_set]
    return premises, hypotheses, labels
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

现在让我们打印前3对前提和假设，以及它们的标签（“0”“1”和“2”分别对应于“蕴涵”“矛盾”和“中性”）

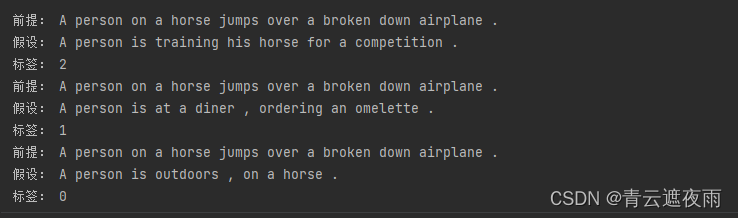
训练集约有550000对，测试集约有10000对。下面显示了训练集和测试集中的三个标签“蕴涵”“矛盾”和“中性”是平衡的。

定义用于加载数据集的类

下面我们来定义一个用于加载SNLI数据集的类。类构造函数中的变量num_steps指定文本序列的长度，使得每个小批量序列将具有相同的形状。换句话说，在较长序列中的前num_steps个标记之后的标记被截断，而特殊标记“”将被附加到较短的序列后，直到它们的长度变为num_steps。通过实现__getitem__功能，我们可以任意访问带有索引idx的前提、假设和标签。

#@save
class SNLIDataset(torch.utils.data.Dataset):
    """用于加载SNLI数据集的自定义数据集"""
    def __init__(self, dataset, num_steps, vocab=None):
        self.num_steps = num_steps
        all_premise_tokens = d2l.tokenize(dataset[0])
        all_hypothesis_tokens = d2l.tokenize(dataset[1])
        if vocab is None:
            self.vocab = d2l.Vocab(all_premise_tokens + \
                all_hypothesis_tokens, min_freq=5, reserved_tokens=['<pad>'])
        else:
            self.vocab = vocab
        self.premises = self._pad(all_premise_tokens)
        self.hypotheses = self._pad(all_hypothesis_tokens)
        self.labels = torch.tensor(dataset[2])
        print('read ' + str(len(self.premises)) + ' examples')

    def _pad(self, lines):
        return torch.tensor([d2l.truncate_pad(
            self.vocab[line], self.num_steps, self.vocab['<pad>'])
                         for line in lines])

    def __getitem__(self, idx):
        return (self.premises[idx], self.hypotheses[idx]), self.labels[idx]

    def __len__(self):
        return len(self.premises)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

这段代码定义了一个名为"SNLIDataset"的自定义数据集类，用于加载SNLI数据集。

构造函数__init__(self, dataset, num_steps, vocab=None)接受三个参数：

• dataset：SNLI数据集，包含了前提、假设和标签的数据。
• num_steps：每个样本的固定长度，用于填充或截断序列。
• vocab：词汇表对象，用于构建词汇表。如果为None，则根据数据集自动构建。

在构造函数中，首先对前提和假设句子进行分词处理，得到所有前提和假设句子的token列表。然后根据是否提供了词汇表对象，初始化了self.vocab属性，该属性是一个词汇表对象。

接下来，调用了self._pad(all_premise_tokens)和self._pad(all_hypothesis_tokens)方法，对前提和假设句子进行填充操作，将其转换为固定长度的序列，并用<pad>进行填充。

最后，将标签转换为torch.tensor对象，并存储在self.labels属性中。同时打印读取的样本数量。

_pad(self, lines)是一个辅助方法，用于将序列进行填充操作。它接受一个列表lines，其中每个元素是一个句子的token列表。对于每个句子，首先使用词汇表将其转换为对应的索引序列，然后使用d2l.truncate_pad方法将序列截断或填充为固定长度num_steps。最后将所有处理后的句子序列转换为一个torch.tensor对象。

__getitem__(self, idx)方法用于获取指定索引的样本。它返回一个元组，包含前提句子、假设句子和对应的标签。

__len__(self)方法返回数据集的样本数量，即前提和假设句子的数量。

整合方法

现在，我们可以调用read_snli函数和SNLIDataset类来下载SNLI数据集，并返回训练集和测试集的DataLoader实例，以及训练集的词表。值得注意的是，我们必须使用从训练集构造的词表作为测试集的词表。因此，在训练集中训练的模型将不知道来自测试集的任何新词元。

#@save
def load_data_snli(batch_size, num_steps=50):
    """下载SNLI数据集并返回数据迭代器和词表"""
    num_workers = d2l.get_dataloader_workers()
    data_dir = d2l.download_extract('SNLI')
    train_data = read_snli(data_dir, True)
    test_data = read_snli(data_dir, False)
    train_set = SNLIDataset(train_data, num_steps)
    test_set = SNLIDataset(test_data, num_steps, train_set.vocab)
    train_iter = torch.utils.data.DataLoader(train_set, batch_size,
                                             shuffle=True,
                                             num_workers=num_workers)
    test_iter = torch.utils.data.DataLoader(test_set, batch_size,
                                            shuffle=False,
                                            num_workers=num_workers)
    return train_iter, test_iter, train_set.vocab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在这里，我们将批量大小设置为128时，将序列长度设置为50，并调用load_data_snli函数来获取数据迭代器和词表。然后我们打印词表大小。

train_iter, test_iter, vocab = load_data_snli(128, 50)
len(vocab)
1
2

现在我们打印第一个小批量的形状。与情感分析相反，我们有分别代表前提和假设的两个输入X[0]和X[1]。

使用注意力机制

鉴于许多模型都是基于复杂而深度的架构，Parikh等人提出用注意力机制解决自然语言推断问题，并称之为“可分解注意力模型” (Parikh et al., 2016)。这使得模型没有循环层或卷积层，在SNLI数据集上以更少的参数实现了当时的最佳结果。本节将描述并实现这种基于注意力的自然语言推断方法（使用MLP）

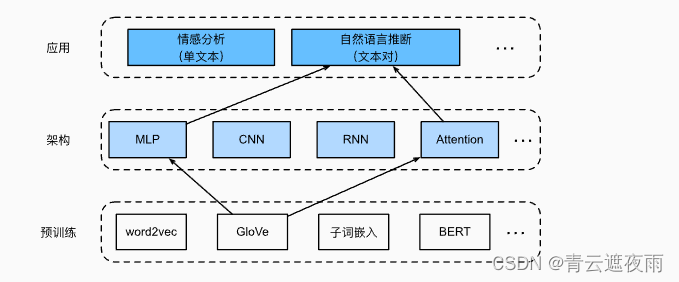
模型

与保留前提和假设中词元的顺序相比，我们可以将一个文本序列中的词元与另一个文本序列中的每个词元对齐，然后比较和聚合这些信息，以预测前提和假设之间的逻辑关系。与机器翻译中源句和目标句之间的词元对齐类似，前提和假设之间的词元对齐可以通过注意力机制灵活地完成。

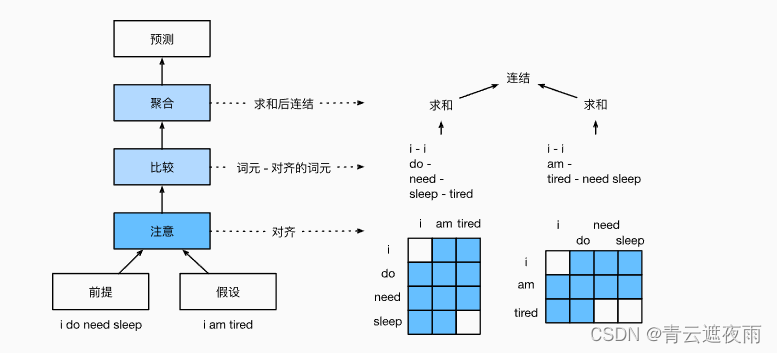
上图描述了使用注意力机制的自然语言推断方法。从高层次上讲，它由三个联合训练的步骤组成：对齐、比较和汇总。我们将在下面一步一步地对它们进行说明。

注意

第一步是将一个文本序列中的词元与另一个序列中的每个词元对齐。假设前提是“我确实需要睡眠”，假设是“我累了”。由于语义上的相似性，我们不妨将假设中的“我”与前提中的“我”对齐，将假设中的“累”与前提中的“睡眠”对齐。同样，我们可能希望将前提中的“我”与假设中的“我”对齐，将前提中的“需要”和“睡眠”与假设中的“累”对齐。请注意，这种对齐是使用加权平均的“软”对齐，其中理想情况下较大的权重与要对齐的词元相关联。为了便于演示， 上图以“硬”对齐的方式显示了这种对齐方式。

现在，我们更详细地描述使用注意力机制的软对齐。用$A=(a_1,...,a_m)$和$B=(b_1,...,b_n)$表示前提和假设，其词元数量分别为$m$和$n$，其中$a_i,b_j\in R^d$（$i=1,...,m,j=1,...,n$）是$d$维的词向量。对于软对齐，我们将注意力权重$e_{ij}\in R$计算为：
$$e_{ij}=f(a_i{)}^{⊺}f(b_j)$$
其中函数$f$是在下面的mlp函数中定义的多层感知机。输出维度$f$由mlp的num_hiddens参数指定。

def mlp(num_inputs, num_hiddens, flatten):
    net = []
    net.append(nn.Dropout(0.2))
    net.append(nn.Linear(num_inputs, num_hiddens))
    net.append(nn.ReLU())
    if flatten:
        net.append(nn.Flatten(start_dim=1))
    net.append(nn.Dropout(0.2))
    net.append(nn.Linear(num_hiddens, num_hiddens))
    net.append(nn.ReLU())
    if flatten:
        net.append(nn.Flatten(start_dim=1))
    return nn.Sequential(*net)
1
2
3
4
5
6
7
8
9
10
11
12
13

对上式中的注意力权重进行规范化，我们计算假设中所有词元向量的加权平均值，以获得假设的表示，该假设与前提中索引$i$的词元进行软对齐：
$${\beta }_i=\sum _{j=1}^n\frac{exp(e_{ij})}{{\sum }_{k=1}^{n}exp(e_{ik})}{b}_j$$
同样，我们计算假设中索引为$j$的每个词元与前提词元的软对齐：
$${\alpha }_i=\sum _{i=1}^m\frac{exp(e_{ij})}{{\sum }_{k=1}^{n}exp(e_{kj})}{a}_i$$
下面，我们定义Attend类来计算假设（beta）与输入前提A的软对齐以及前提（alpha）与输入假设B的软对齐。

class Attend(nn.Module):
    def __init__(self, num_inputs, num_hiddens, **kwargs):
        super(Attend, self).__init__(**kwargs)
        self.f = mlp(num_inputs, num_hiddens, flatten=False)

    def forward(self, A, B):
        # A/B的形状：（批量大小，序列A/B的词元数，embed_size）
        # f_A/f_B的形状：（批量大小，序列A/B的词元数，num_hiddens）
        f_A = self.f(A)
        f_B = self.f(B)
        # e的形状：（批量大小，序列A的词元数，序列B的词元数）
        e = torch.bmm(f_A, f_B.permute(0, 2, 1))
        # beta的形状：（批量大小，序列A的词元数，embed_size），
        # 意味着序列B被软对齐到序列A的每个词元(beta的第1个维度)
        beta = torch.bmm(F.softmax(e, dim=-1), B)
        # beta的形状：（批量大小，序列B的词元数，embed_size），
        # 意味着序列A被软对齐到序列B的每个词元(alpha的第1个维度)
        alpha = torch.bmm(F.softmax(e.permute(0, 2, 1), dim=-1), A)
        return beta, alpha
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

比较

在下一步中，我们将一个序列中的词元与与该词元软对齐的另一个序列进行比较。请注意，在软对齐中，一个序列中的所有词元（尽管可能具有不同的注意力权重）将与另一个序列中的词元进行比较。

在比较步骤中，我们将来自一个序列的词元的连结（运算符$[.,.]$）和来自另一序列的对齐的词元送入函数$g$（一个多层感知机）：
$$\begin{gathered} v_{A,i}=g([{\alpha }_i,{\beta }_i]),i=1,...,m \\ {v}_{B,j}=g([{\beta }_j,{\alpha }_j]),j=1,...,n \end{gathered}$$
$v_{A,i}$是指，所有假设中的词元与前提中词元$i$软对齐，再与词元$i$的比较；而$v_{B,j}$是指，所有前提中的词元与假设中词元$j$软对齐，再与词元$j$的比较。下面的Compare个类定义了比较步骤。

class Compare(nn.Module):
    def __init__(self, num_inputs, num_hiddens, **kwargs):
        super(Compare, self).__init__(**kwargs)
        self.g = mlp(num_inputs, num_hiddens, flatten=False)

    def forward(self, A, B, beta, alpha):
        V_A = self.g(torch.cat([A, beta], dim=2))
        V_B = self.g(torch.cat([B, alpha], dim=2))
        return V_A, V_B
1
2
3
4
5
6
7
8
9

聚合

现在我们有两组比较向量$v_{A,i}$（$i=1,...,m$）和$v_{B,j}$（$j=1,...,n$）。在最后一步中，我们将聚合这些信息以推断逻辑关系。我们首先求和这两组比较向量：
$$v_A=\sum _{i=1}^m{v}_{A,i},v_B=\sum _{j=1}^n{v}_{B,j}$$
接下来，我们将两个求和结果的连结提供给函数$h$（一个多层感知机），以获得逻辑关系的分类结果：
$$y=h([v_A,v_B])$$
聚合步骤在以下Aggregate类中定义。

class Aggregate(nn.Module):
    def __init__(self, num_inputs, num_hiddens, num_outputs, **kwargs):
        super(Aggregate, self).__init__(**kwargs)
        self.h = mlp(num_inputs, num_hiddens, flatten=True)
        self.linear = nn.Linear(num_hiddens, num_outputs)

    def forward(self, V_A, V_B):
        # 对两组比较向量分别求和
        V_A = V_A.sum(dim=1)
        V_B = V_B.sum(dim=1)
        # 将两个求和结果的连结送到多层感知机中
        Y_hat = self.linear(self.h(torch.cat([V_A, V_B], dim=1)))
        return Y_hat
1
2
3
4
5
6
7
8
9
10
11
12
13

整合代码

通过将注意步骤、比较步骤和聚合步骤组合在一起，我们定义了可分解注意力模型来联合训练这三个步骤。

class DecomposableAttention(nn.Module):
    def __init__(self, vocab, embed_size, num_hiddens, num_inputs_attend=100,
                 num_inputs_compare=200, num_inputs_agg=400, **kwargs):
        super(DecomposableAttention, self).__init__(**kwargs)
        self.embedding = nn.Embedding(len(vocab), embed_size)
        self.attend = Attend(num_inputs_attend, num_hiddens)
        self.compare = Compare(num_inputs_compare, num_hiddens)
        # 有3种可能的输出：蕴涵、矛盾和中性
        self.aggregate = Aggregate(num_inputs_agg, num_hiddens, num_outputs=3)

    def forward(self, X):
        premises, hypotheses = X
        A = self.embedding(premises)
        B = self.embedding(hypotheses)
        beta, alpha = self.attend(A, B)
        V_A, V_B = self.compare(A, B, beta, alpha)
        Y_hat = self.aggregate(V_A, V_B)
        return Y_hat
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

训练和评估模型

现在，我们将在SNLI数据集上对定义好的可分解注意力模型进行训练和评估。我们从读取数据集开始。

读取数据集

批量大小和序列长度分别设置为$256$和$50$。

batch_size, num_steps = 256, 50
train_iter, test_iter, vocab = d2l.load_data_snli(batch_size, num_steps)
1
2

创建模型

我们使用预训练好的100维GloVe嵌入来表示输入词元。我们将向量$a_i$和$b_j$中的维数预定义为100。函数$f$和函数$g$的输出维度被设置为200.然后我们创建一个模型实例，初始化它的参数，并加载GloVe嵌入来初始化输入词元的向量。

embed_size, num_hiddens, devices = 100, 200, d2l.try_all_gpus()
net = DecomposableAttention(vocab, embed_size, num_hiddens)
glove_embedding = d2l.TokenEmbedding('glove.6b.100d')
embeds = glove_embedding[vocab.idx_to_token]
net.embedding.weight.data.copy_(embeds);
1
2
3
4
5

训练和评估模型

我们定义了一个split_batch_multi_inputs函数以小批量接受多个输入，如前提和假设。

lr, num_epochs = 0.001, 4
trainer = torch.optim.Adam(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss(reduction="none")
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs,
    devices)
1
2
3
4
5

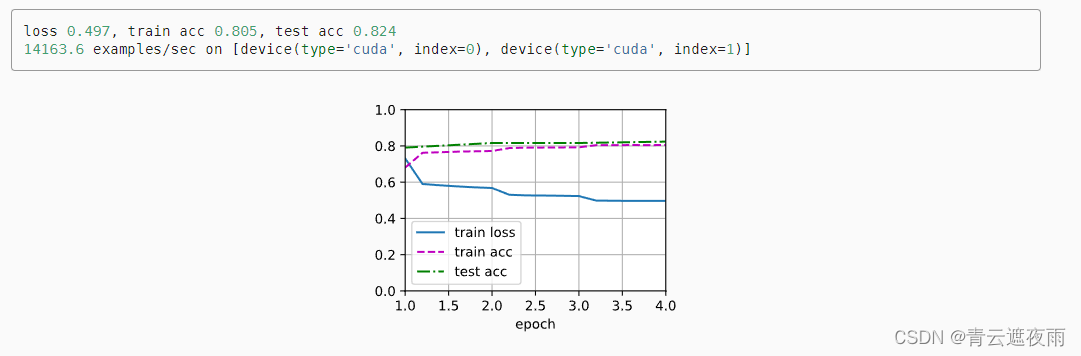
使用模型

最后，定义预测函数，输出一对前提和假设之间的逻辑关系。

#@save
def predict_snli(net, vocab, premise, hypothesis):
    """预测前提和假设之间的逻辑关系"""
    net.eval()
    premise = torch.tensor(vocab[premise], device=d2l.try_gpu())
    hypothesis = torch.tensor(vocab[hypothesis], device=d2l.try_gpu())
    label = torch.argmax(net([premise.reshape((1, -1)),
                           hypothesis.reshape((1, -1))]), dim=1)
    return 'entailment' if label == 0 else 'contradiction' if label == 1 \
            else 'neutral'
1
2
3
4
5
6
7
8
9
10

我们可以使用训练好的模型来获得对示例句子的自然语言推断结果。

predict_snli(net, vocab, ['he', 'is', 'good', '.'], ['he', 'is', 'bad', '.'])
1