devbox
码创造者
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

leetcode刷题笔记2-数组_查找数组中与target相同的数,并将其下表赋值给指针idx

作者：码创造者 | 2024-07-05 02:03:13

赞

踩

查找数组中与target相同的数,并将其下表赋值给指针idx

数组

代码随想录刷题笔记

代码随想录 (programmercarl.com)

理论基础

1.1 数组在内存中的存储方式

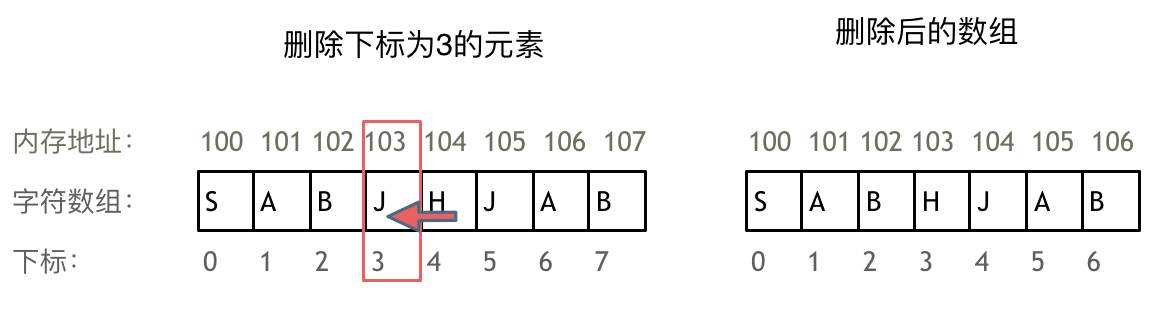
数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

注意：

  • 数组下标都是从0开始的。

  • 数组内存空间的地址是连续的

    • 在删除或者增添元素的时候，就要移动其他元素的地址。

      img

  • C++中：vector和array区别：

    • vector的底层实现是array，严格来讲vector是容器，不是数组。

  • 数组的元素是不能删的，只能覆盖。

1.2 二维数组：

二维数组在内存的空间地址是连续的么？

不同编程语言的内存管理是不一样的

C++中二维数组是连续分布的。

数组内存

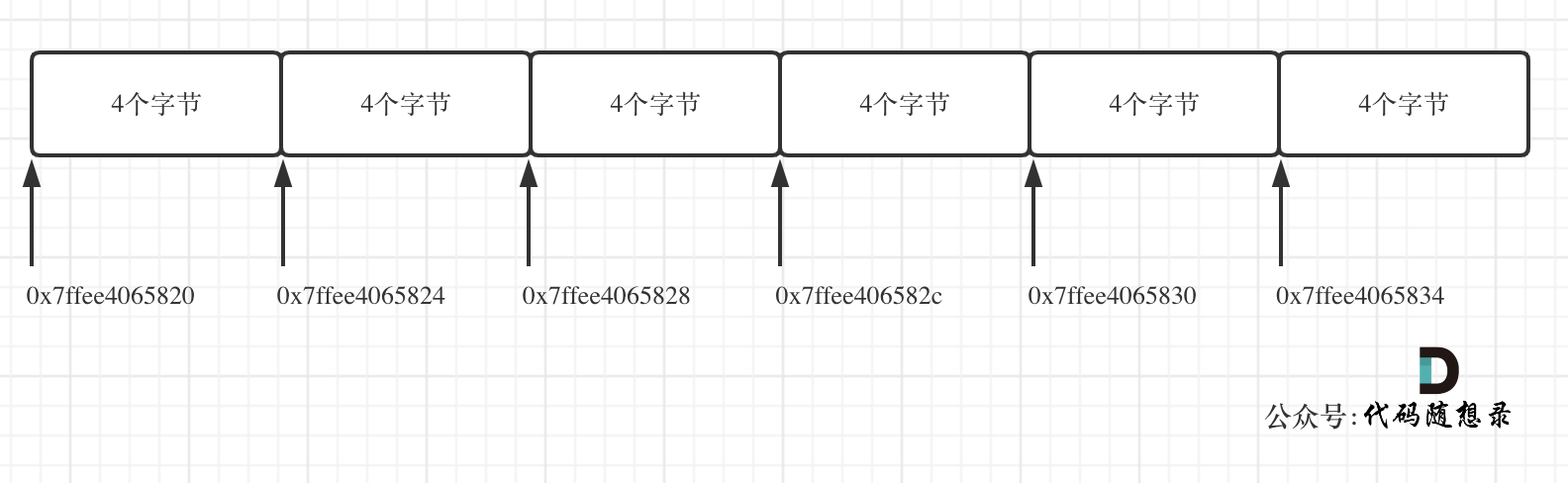
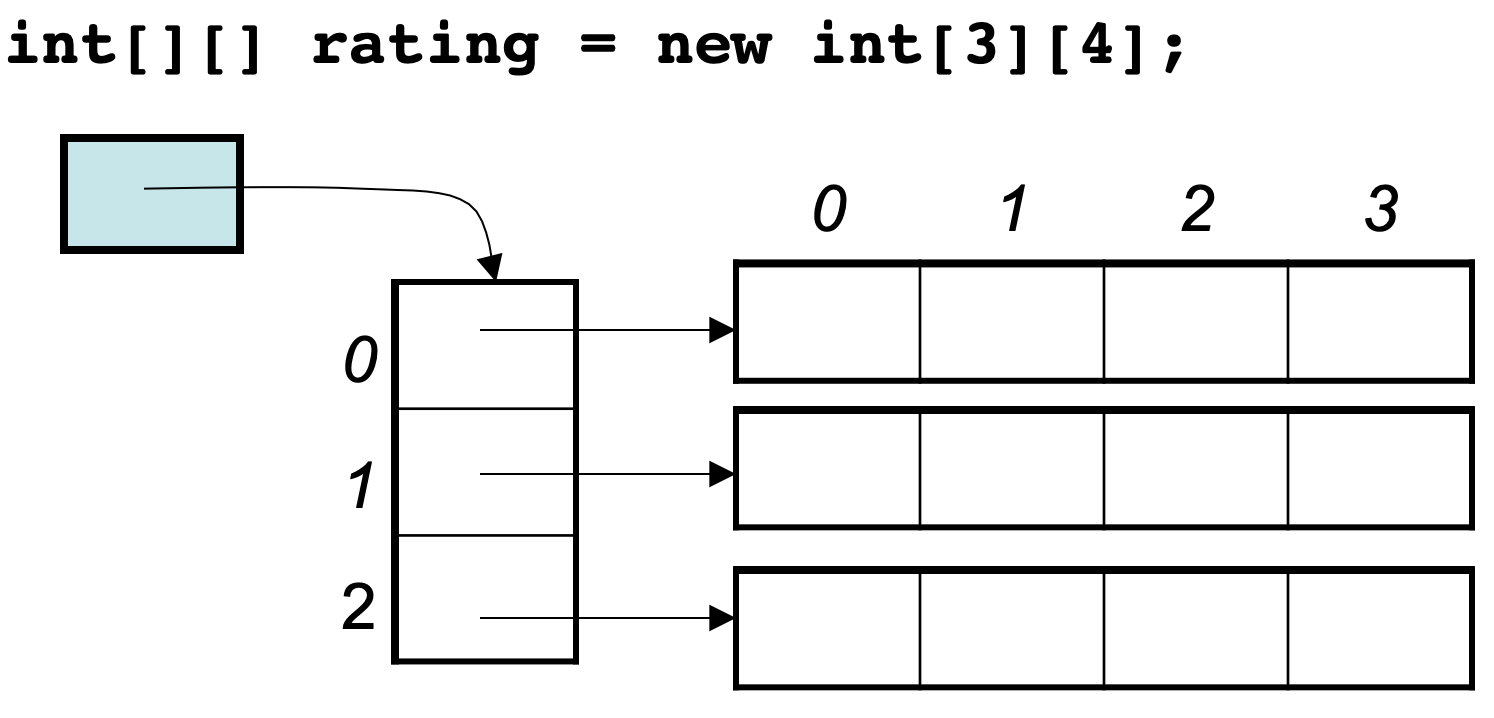
Java中，没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。二维数组的每一行头结点的地址是没有规则的，更谈不上连续。

Java的二维数组在内存中不是 3\*4 的连续地址空间，而是四条连续的地址空间组成！

算法通关数组3

1.3 c++ vector (一维，二维的初始)使用

vector类似于一个动态数组，当不确定所要使用的数组的大小的时候，可以使用vector。

vector可以动态的改变大小。

1.一维vector的创建及使用

(1)头文件

include<vector> //头文件

(2)创建vector对象并初始

vector<int>nums（a,0）; //创建大小为a的nums数组并初始化为0
(3)在尾部插入元素

nums.push_back(1); //在尾部插入值为1的元素
(4)指定位置插入元素

nums.insert(nums.begin()+1,9); //在nums的nums[1]位置插入元素9 如1,2,3,4 插入为 1,9,2,3,4
nums.insert(nums.begin()+1,3,9); //在nums的nums[1]位置插入3个数，值都为9
（5）删除尾部最后一个元素

nums.pop_back(); //删除尾部元素
(6) 删除第i个元素（删除后的数组重新排列 如删除之前nums[2]=3，删除nums[1]后，删除后的nums中nums[1]=3.）

nums.erase(nums.begin()+2) //删除第3个元素(删除nums[2])

//删除注意

#include<iostream>

#include<vector>

using namespace std;
int main()
{
	vector<int>nums(4,0);
	nums[0] = 1;
	nums[1] = 2;
	nums[2] = 3;
	nums[3] = 4;
	nums.erase(nums.begin()+1); //删除nums[1]
	cout <<  nums[1]; //nums[2]前移  这时nums[1]为nums[2]的值
 	return 0;
}
// 输出nums[1]为 3

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19

(7)删除区间元素

nums.erase(nums.beigin()+1,nums.begin()+3); //删除nums中nums[1]元素到nums[2]元素
(8)大小

nums.size();
(9)清空

nums.clear();
(10)判断是否为空

nums.empty();

2.二维vector的初始
#include<iostream>

using namespace std;

#include<vector>

int main()
{
	int a, b;
	cin >> a >> b;
	vector<vector<int>>nums(a, vector<int>(b);//创建一个二维动态数组nums[a][b]，并初始化为0；
	                                          //若初始化为1，将(b)改为(b,1) 
int n=nums.size() ; //行数
int m=nums[0].size(); //列数

}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

二分查找

**前提：**1. 有序数组

​ 2. 数组中无重复元素（如果有返回的元素下标可能不唯一）

解题思路：

  1. 设定左右指针

  2. 找出中间位置，并判断该位置值是否等于 target

  3. nums[mid] == target 则返回该位置下标
    nums[mid] > target 则右侧指针移到中间
    nums[mid] < target 则左侧指针移到中间

  4. 时间复杂度：O(logN)

  5. 解题框架

    int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;	//计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防止了 left 和 right 太大直接相加导致溢出。
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15

混淆点：

​ 边界条件的选择。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

解决方法：

  1. 确定区间（循环不变量）

    左闭右闭？左闭右开？

  2. 根据区间，从而选择边界条件

（1）左闭右开：

left = 0；

right = numsize - 1；

while (left <= right)

if (nums[middle] > target) right 要赋值为 middle - 1

if (nums[middle] < target) left 要赋值为 middle + 1

  • while（left right）条件判断是小于等于？还是小于？

思考：当[left, right]取left=right时，合不合法？例如当left=right=1，[1,1]区间包含1，是合法的，所以可以取等号，即：while（left <= right）

  • 当nums[middle]>target时，是right = middle?还是right = middle - 1呢？

思考：区间：左闭右闭；条件nums[middle]>target。左闭右闭说明一定包含right；条件则说明nums[middle]一定大于target，所以nums[middle]一定不是寻找的值target，所以下一步区间选择right = middle - 1

  • 同理，当nums[middle]<target时，是left = middle?还是left = middle + 1呢？

思路同上，所以下一步区间选择left = middle + 1

class Solution {
public:
    int search(vector<int>& nums, int target) {
        //左闭右闭区间解法
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right){
            int middle = left + ((right - left) / 2);   //防止溢出，等同于(left + right)/2
            if(nums[middle] > target) {
                right = middle - 1;
            } else if(nums[middle] < target) {
                left = middle + 1;
            } else {
                return middle;  //找到目标值，返回下标
            } 
        }
        return -1;  //未找到目标值，返回-1
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19

（2）左闭右开：

left = 0;

right = numsize;

while (left < right)

if (nums[middle] > target) right 要赋值为 middle

if (nums[middle] < target) left 要赋值为 middle + 1

  • while（left right）条件判断是小于等于？还是小于？

思考：当[left, right）取left=right时，合不合法？例如当left=right=1时，[1,1）区间代表又包含有不包含1，是不合法的，所以不可以取等号，即：while（left < right）

  • 当nums[middle]>target时，是right = middle?还是right = middle - 1呢？

思考：区间：左闭右开；条件：nums[middle]>target。则因为接下来的搜索区间本来就不包含right，并且条件中nums[middle]>target说明下一次搜索的左区间也不包含nums[middle]，（即下一个查询区间不会去比较nums[middle]），所以下一步区间选择right = middle

  • 当nums[middle]<target时，是left = middle?还是left = middle + 1呢？

思考：区间：左闭右开；条件：nums[middle]>target。左闭所以包含了left，但是条件中nums[middle]<target说明下一次搜索不包含nums[middle]，所以下一步区间选择left = middle + 1

class Solution {
public:
    int search(vector<int>& nums, int target) {
        //左闭右开区间解法
        int left = 0;
        int right = nums.size();
        while(left < right){
            int middle = left + ((right - left) / 2);   //防止溢出，等同于(left + right)/2
            if(nums[middle] > target) {
                right = middle ;
            } else if(nums[middle] < target) {
                left = middle + 1;
            } else {
                return middle;  //找到目标值，返回下标
            } 
        }
        return -1;  //未找到目标值，返回-1
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19

总结：

  1. while（left right）选择小于或小于等于时，将等于（即left= right = 1）条件带入，判断是否合法（[1,1]合法，[1,1）不合法）

  2. 选择right = middle?还是right = middle - 1？

    选择left = middle?还是left = middle + 1？

    遇到闭区间一侧，则需要+或-1

    遇到开区间一侧，则不需要+或-1

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4     

  • 1
  • 2
  • 3

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1        

  • 1
  • 2
  • 3

提示：

  • 你可以假设 nums 中的所有元素是不重复的。
  • n 将在 [1, 10000]之间。
  • nums 的每个元素都将在 [-9999, 9999]之间。

**解题思路：**使用以上模板进行二分查找即可。

相关练习题：

二分查找法变式1：找出第一个大于等于目标元素的索引

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。—>二分查找

解题思路：

本题不同于原型之处在于，如果目标值**不存在于数组中，返回它将会被按顺序插入的位置。**另一种解读也就是：返回第一个大于或等于target元素的下标。

也就分为两种情况，

当数组中存在target时，与原型相同。

当数组中不存在target时，如何处理？其实也就是改变一下while后return值即可。将原型中的return -1，改变为：

  1. 当左闭右闭时，return right +1 或return left
  2. 当左闭右开时，return right即可

第一种写法为什么最后返回right+1？因为判断条件是left<=right，所以结束的时候有left = right + 1，然后又因为target插入的位置是数组中第一个大于target元素的位置，所以应该返回的right+1和left其实是等价的。

二分法参考代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right){
            int middle = left + ((right - left) / 2);
            if(nums[middle] > target){
                right = middle - 1;
            } else if(nums[middle] < target){
                left = middle + 1;
            } else {
                return middle;
            }
        }
        return left;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XXwZJioT-1680080333635)(…/…/…/lenovo/AppData/Roaming/Typora/typora-user-images/image-20220725174516368.png)]

其实，这道题如果不限制时间复杂度为 O(log n) 的算法，使用暴力解法更快。

暴力解题 不一定时间消耗就非常高，关键看实现的方式，就像是二分查找时间消耗不一定就很低，是一样的。

暴力解法代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        for (int i = 0; i < nums.size(); i++) {
        // 分别处理如下三种情况
        // 目标值在数组所有元素之前
        // 目标值等于数组中某一个元素
        // 目标值插入数组中的位置
            if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
                return i;
            }
        }
        // 目标值在数组所有元素之后的情况
        return nums.size(); // 如果target是最大的，或者 nums为空，则返回nums的长度
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

效率如下：

35_搜索插入位置

二分查找法变式2：找出元素的第一个位置和最后一个位置（数组中有重复元素）

34. 在排序数组中查找元素的第一个和最后一个位置

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/solution/yi-wen-dai-ni-gao-ding-er-fen-cha-zhao-j-ymwl/（优秀题解）

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

在原型中的前提条件是数组中没有重复元素，以上变式是数组中存在重复元素，则需要返回对应区间，也就是要找到目标元素的第一个（下边界）和最后一个位置（上边界）

解题思路：

  1. 寻找目标元素下边界：

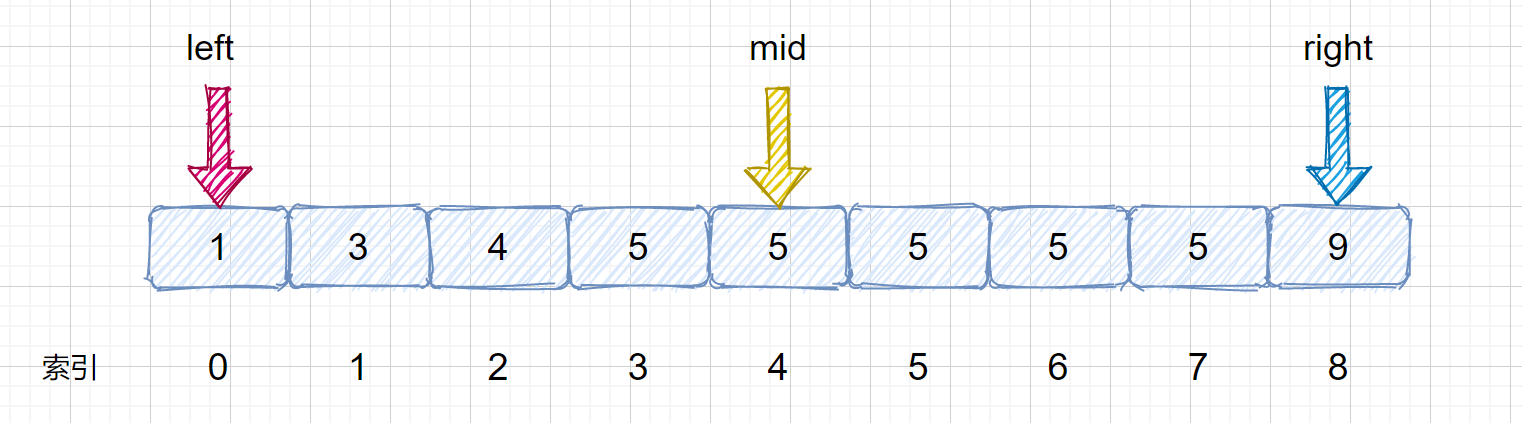
二分查找下边界

考虑到这种情况时（target = 5），mid所指位置并不是第一个5，所以需要继续寻找，而不是返回当前位置，如何做呢？需要改变的是判断条件，也就是当target = nums[mid]也让 right = mid - 1。即可以合并为target <= nums[mid] 时，让 right = mid - 1即可。还需要注意的就是，我们计算下边界时最后的返回值为 left

计算下边界代码

    int getLeftBound(vector<int>& nums, int target) {
        int left = 0; 
        int right = nums.size() - 1;
        while(left <= right){
            //这里需要注意，计算mid
            int mid = left + ((right - left) / 2);
            if(nums[mid] >= target){
                //当目标值小于等于nums[mid]时，继续在左区间检索，找到第一个数
                right = mid - 1;
            } else {
                //目标值大于nums[mid]时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1;
            }
        }
        return left;
    }

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  1. 寻找目标元素上边界：

与寻找下边界相反。

当target = nums[mid]改为让 left = mid + 1。即可以合并为target >= nums[mid] 时，让 left = mid + 1即可。

计算上边界代码

    int getRightBound(vector<int>& nums, int target) {
        int left = 0; 
        int right = nums.size() - 1;
        while(left <= right){
            int mid = left + ((right - left) / 2);
            if(nums[mid] > target){
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

总结一下：

计算下边界时，当 target <= nums[mid] 时，right = mid -1；target > nums[mid] 时，left = mid + 1；

计算上边界时，当 target < nums[mid] 时，right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反，返回right。

完整参考代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int left = getLeftBound(nums, target);
        int right = getRightBound(nums, target);
        //如果数组中不存在target
        if(left > right){
            return {-1, -1};
        }
        return {left, right};
    }

private:
    int getLeftBound(vector<int>& nums, int target) {
        int left = 0; 
        int right = nums.size() - 1;
        while(left <= right){
            int mid = left + ((right - left) / 2);
            if(nums[mid] >= target){
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
    int getRightBound(vector<int>& nums, int target) {
        int left = 0; 
        int right = nums.size() - 1;
        while(left <= right){
            int mid = left + ((right - left) / 2);
            if(nums[mid] > target){
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return right;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
69. x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

解题思路：

题解1：二分查找法

不能使用内置函数，所以我们需要寻找一个整数，使得：

如果这个整数的平方 恰好等于 输入整数，那么我们就找到了这个整数；

如果这个整数的平方 严格大于 输入整数，那么这个整数肯定不是我们要找的那个数；

如果这个整数的平方 严格小于 输入整数，那么这个整数 可能 是我们要找的那个数（重点理解这句话）（也就是题解1中为什么要ans = mid的原因）。

应此，由以上思路，即可分析出，这道题可以使用二分查找法来查找这个整数，不断缩小范围去猜。

初始范围：[0, x / 2];

还需要注意的是，

  1. mid * mid 防止溢出解决方法：

    （1）mid <= x / mid

    （2）(long long)mid * mid <= x

  2. if else条件判断

​ 当mid * mid <= x时，说明有可能答案在[mid, r]之中，有可能是mid，所以可以巧用ans，将mid暂存，接下来将l = mid + 1;也就是[mid + 1, r]中搜索是否有符合条件的结果，如果有，则更新ans，如果没有，则答案就是上一步暂存的ans。

​ 然而当mid * mid > x时，答案一定不在该范围内[mid, r] ，所以直接r = mid - 1;

二分查找法参考代码：

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x) {    //防止溢出
                ans = mid;  //将上一步得到的可能值存放在ans中（防止下一步l移动后，可能ans就是答案）
                l = mid + 1;
            } else {    //当mid * mid > x时，ans一定不再该区间内，所以mid - 1；
                r = mid - 1;
            }
        }
        return ans;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

题解2：牛顿迭代法

推导公式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pxydmA9S-1680080333636)(…/…/…/lenovo/AppData/Roaming/Typora/typora-user-images/image-20220726191032275.png)]

牛顿迭代法参考代码：

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (fabs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return int(x0);
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18

双指针

27. 移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

解题思路：

因为数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

所以这道题，其实也就是在**模拟vector库函数中，erase()**封装好的操作。

有两种解法：

题解1：暴力解法

使用两层for循环，第一层for循环负责遍历元素，找出目标值对应位置。第二层for循环负责更新数组，将找到对应位置之后的所有元素都向前移动一个位置，也就是进行覆盖操作。

时间复杂度：O(n^2)

空间复杂度：O(1)

暴力解法参考代码：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        //暴力解法
        int size = nums.size();
        for(int i = 0; i < size; i++){   //第一层负责遍历元素
            if(nums[i] == val){     //找到对应位置
                for(int j = i; j < size - 1; j++){  //这里要注意了， j < size - 1，因为要移动的最后一个元素是下标为size - 1位置上的元素，而不是下标为size，就没有这个元素
                    nums[j] = nums[j + 1];
                }
            i--;    //这里要注意了，因为i之后所有元素都向前移动一位，所以在i位置上又有新的数字，也有可能是val，所以需要i--，重新比较
            size--;
            }
        }
        return size;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17

题解二：快慢指针解法

快慢指针（双指针）：**通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。**常见于数组、链表、字符串等操作中。

关键：定义快慢指针所代表的意义

  • 快指针：寻找新数组的元素（不含有val的所有元素）

  • 慢指针：指向需要更新新数组下标的位置（将快指针所指的需要的元素，放到慢指针所指位置中）

时间复杂度：O(n)、空间复杂度：O(1)

快慢指针参考代码：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slow = 0;   //初始化慢指针位置（快指针在for循环中初始化）
        for(int fast = 0; fast < nums.size(); fast++) {
            if(nums[fast] != val){  
                //如果fast所指位置的元素不等于val，则更新数组，将该元素赋值给slow指针所指位置（新数组中该元素应该覆盖的位置）
                nums[slow++] = nums[fast];  //实现两个操作：1. 将fast所指位置元素覆盖到slow所指需要更新位置 2. 执行完覆盖操作后，将slow后移一位（slow++），指向下一次数组要更新的位置

            }
        }
        return slow;    //最终slow所指的位置，就是数组的size
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

其实这道题有个更简单的思路，

因为题目的要求是元素的顺序可以改变。

我们可以将数组分成「前后」两段：

前半段是有效部分，存储的是不等于 val 的元素。
后半段是无效部分，存储的是等于 val 的元素。
最终答案返回有效部分的结尾下标。

所以，从左边找到和val相等元素位置时，只需要与该数组右边不等于val的元素交换（swap）即可，不需要将val后所有元素移动一位

也就是以下参考代码：（但是拷贝覆盖也就是上一个代码实现比较通用）

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int right = nums.size() - 1;
        for(int left = 0; left <= right; left++){
            if(nums[left] == val){
                swap(nums[left--], nums[right--]);  //交换后，将left--，right--
                //left--目的：有可能交换过来的值等于val，所以要重新扫描一下这个位置的值
                //right--目的：将右边指针向左移一位，也就是指向右边第一个不等于val的值
            }
        }
        return right + 1;   //数组大小等于有效部分（存储的是不等于 val 的元素）的大小，也就是right指向位置+1
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
26. 删除有序数组中的重复项

给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

解题思路：

使用快慢指针法，

  • 快指针：寻找与s慢指针不相等元素的位置

  • 慢指针：指向新数组元素更新的位置的前一位

每次判断快慢指针所指元素是否相等，

  • 相等：快指针后移一位继续寻找

  • 不相等：赋值，将快指针所指元素赋值给慢指针（++slow而不是slow++，因为slow指向的是相等元素位置，而下一个不相等元素位置（fast）是slow之后一位）

重复，直到快指针遍历完所有元素

注意：

  1. 边界：当数组的长度等于0时，不需要操作，直接返回0即可。

  2. 初始化条件：

    快指针用于遍历数组，但第一个元素不需要检查，也就是只需要比较第二个元素和第一个是否相等即可，所以快指针初始值为1；

    初始状态下，慢指针应该是在快指针前一位，所以初始值为0；

  3. 结束条件：当快指针达到数组尾部时，程序结束，返回当前slow + 1；即更新后数组长度。

参考代码：

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int length = nums.size();
        if (length == 0) return 0;
        int slow = 0, fast = 1; //初始化slow指向第一个元素，fast从第二个元素开始，才能判断slow和fast所指元素是否相等。
        while (fast < length) {
            if (nums[fast] != nums[slow]) {
                nums[++slow] = nums[fast];  //注意是++slow，因为，slow存放的是相等元素的位置，而此时赋值时将不相等元素赋给下一个位置
            }
            fast++; //不管想不想的，每次循环快指针都需要向后移动一位
        }
        return slow + 1;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
80. 删除有序数组中的重复项 II

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

为了让解法更具有一般性，我们将原问题的「保留 2 位」修改为「保留 k 位」。

解题思路：

还是使用快慢指针（和26题思路很相似），只是因为要保留k位，那么比较时，检查的是快指针指向的元素和慢指针指向的元素的前（k-1)个元素（也就是nums[slow - ( k - 1)]是否相等。（判断是否相同后的操作与26题相同）

相等，则不更新慢指针，只更新快指针。

不相等，则现将慢指针后移一位，再将快指针指向的元素赋值给慢指针指向的单元，最后更新快指针。

注意：

  1. 边界：当数组的长度小于等于2时，不需要操作，直接返回原数组即可。

  2. 初始化条件：

    快指针用于遍历数组，但前两个元素不需要检查，也就是不需要操作序号小于2的元素，所以快指针初始值为2；

    初始状态下，慢指针应该是在快指针前一位，所以初始值为1；

  3. 结束条件：当快指针达到数组尾部时，程序结束，返回当前slow + 1；即更新后数组长度。

参考代码：（通用解法：k为保留k个相同元素）

class Solution {
public:
    int process(vector<int>& nums, int k) {
        int slow = 1;
        int len = nums.size();
        if(len <= 2)    return len;
        for(int fast = 2; fast < len; fast++){
            if(nums[slow - k + 1] != nums[fast]) {
                nums[++slow] = nums[fast];
            }
        }
        return slow + 1;
    }
    int removeDuplicates(vector<int>& nums) {
        return process(nums, 2);
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
977. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

解题思路：

题解1：暴力排序

这道题，最直接的想法：先将数组全部平方，再讲其排序。

但是时间复杂度为：O(n + nlogn)，也可以说是O(nlogn)的时间复杂度

​ 空间复杂度：O(log n)。除了存储答案的数组以外，我们需要 O(logn) 的栈空间进行排序。

暴力排序参考代码：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> ans;
        for (int num: nums) {
            ans.push_back(num * num);
        }
        sort(ans.begin(), ans.end());
        return ans;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11

题解2：双指针法

由于暴力解决时间复杂度为O(nlogn)，所以为了将时间复杂度调整为O(n)，可以使用双指针解法；具体思路如下：

思考：

当数组全部平方后，最大值在数组两端（负数平方后有可能变成最大数），最小值在数组中间。整体趋势为【大，小，大】。

所以，可以考虑双指针法，两个指针i 指向起始位置，j 指向终止位置。

另外定义一个新数组result，是它和原始数组有一样的空间大小，并且定义一个k使其指向result数组终止位置（因为题目要求从小到大，所以终止位置存放最大数，与i和j扫描数组是从大到小相反，所以从终止位置往前移动依次存放后最终result中数是从小到大的顺序）

具体逻辑：

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。赋值后，j–；

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。赋值后，i++;

（当A[i] * A[i] = A[j] * A[j]时，放在哪个判断条件中都可以）

双指针法参考代码：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> result(nums.size(), 0);    //定义一个新数组，存放最终结果
        int left = 0; 
        int right = nums.size() - 1;
        int k = nums.size() - 1;
        while(left <= right){   //注意此处，判断条件是left <= right，因为当left = right时，也需要进入循环，将对应的平方数存入新数组中，如果没有等于这个条件，则最后一个数字没有执行循环条件无法存入新数组中
            if(nums[left] * nums[left] >= nums[right] * nums[right]){   //l更大，则存left数，left++；
                result[k--] = nums[left] * nums[left];
                left++;
            } else {
                result[k--] = nums[right] * nums[right];
                right--;
            }
        }
        return result;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
88. 合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

解题思路：

本题重点：

  1. 两个数组有序
  2. 合并的结果存放入nums1中，并且nums1的初始长度为m+n，正好可以放下nums1和nums2。

合并这两个数组，自让会想到最简单的做法：归并排序：将两个有序数组合并放到另一个数组中，最终将该数组赋值给nums1即可。（时间复杂度O（m + n） ）

但由于本题中，nums1长度能够保证放下m+n个元素，所以可以直接将合并的结果放入num1中。

于是有以下两种思路：

  1. 将两个数组从开头到结尾开始比较，每次将比较后的数字放到nums1的前面，但是需要把nums1中该位置之后的元素全部向后移动，移动次数比较多。
  2. 将两个数组从结尾到开头开始比较，每次将比较后的数字放到nums1的后面进行交换，由于后面的数字本来就是多余位置为0，因此不需要对nums1进行移动。

因此，思路2更好，即从后向前进行比较。

具体步骤：

  1. 当m > 0 并且n > 0时，从后向前比较num1[m - 1]和 num2[n - 1]：

    如果是 nums1[m - 1]大，则把 nums1[m - 1]放到 num1 的第 m + n - 1 位置，并让 m --。
    如果是 nums1[n - 1]大，则把 nums2[n - 1] 放到 num1 的第 m + n - 1 位置，并让 n --。

  2. 当以上遍历条件结束时，此时m和n至少有一个是0

    当m == 0 时，说明nums2中可能还剩元素，那么将nums2中剩下的元素复制到nums1中头部即可。

    当n == 0 时，说明nums2中数字全部转移到nums1中，此时nums1中可能还剩元素，但是因为nums1本来就是有序，且这些剩余的元素一定是nums1和nums2中最小的元素，所以不需要动，直接留在原地即可。

参考代码：

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int k = m + n - 1;
        while(m > 0 && n > 0){
            if(nums1[m - 1] > nums2[n - 1]){    //如果nums1中所指元素大
                nums1[k] = nums1[m - 1];
                m--;
            } else {
                nums1[k] = nums2[n - 1];
                n--;
            }
            k--;
        }
        for(int i = 0; i < n; i++){ //如果n不为0，也就是nums2中还有元素时，将其直接复制给nums1
            nums1[i] = nums2[i];
        }
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19

滑动窗口

209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

解题思路：

题解1：暴力解法

因为是小白，想到了暴力解决方法，两层for循环，然后不断的寻找符合条件的子序列，所以时间复杂度为O（n^2），导致超时，只能是做个记录参考一下吧。。。

参考代码：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int len = nums.size();
        int temp, min = len + 1;
        for(int i = 0; i < len; i++){
            int sum = 0;
            temp = 0;
            for(int j = i; j < len; j++){
                sum += nums[j];
                temp++;
                if(sum >= target){
                    if(temp < min)  min = temp;
                    break;
                }

            }

        }
        if(min == len + 1){
            return 0;
        }else {
            return min;
        }

    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

题解2：滑动窗口

滑动窗口，是使用两个指针分别指向窗口的首尾位置，通过不断调节首尾位置即窗口大小，从而找到满足条件的最优结果。由于只需要使用一个for循环，所以时间复杂度为O（n）

滑动窗口解决思路如下：

  1. for循环中，表示的是终止位置 j 。（若是起始位置，又回到暴力解法）

  2. 起始位置如何移动？精髓所在！动态调节滑动窗口起始位置 i 。（在循环中，不断变更i，也就是子序列的起始位置）

  3. 实现滑动窗口需要考虑的问题：

    1. 窗口是什么？

      其和大于等于s 的 长度最小的 连续 子数组

    2. 如何移动窗口起始位置？

      当前窗口值大于s，起始位置就向后移动进行缩小。

    3. 如何移动窗口结束位置？

      遍历整个数组，也就是for循环里的索引

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

总结滑动窗口框架：

void slidwindow(vector<int> nums)
{
    int left = 0, right = 0;
    for(right = 0; right < nums.size(); right++)//扩大右边界
    {
        ...//更新窗口状态
        while(需要收缩)//窗口到达什么状态需要收缩
        {
            ...//缩小左边界并更新窗口状态
            left++;
        }
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

疑惑解答：为什么for循环里套着while循环，时间复杂度不是O(n^2)， 而是O(n)？

时间复杂度，主要看的是每一个元素被操作的次数，每个元素在滑动窗口进入和出去时分别被操作一次，所以时间复杂度是2 * n，也就是O(n)。

本题解题思路：

使用左右指针 left 和 right，left 和 right 之间的长度即为滑动窗口的大小（即连续数组的大小）。
如果滑动窗口内的值 sum >= target，维护连续数组最短长度，left 向右移动，缩小滑动窗口。
如果滑动窗口内的值 sum < target，则 right 向有移动，扩大滑动窗口。

参考代码：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int left = 0;   //表示滑动窗口起始位置
        int sum = 0;    //表示滑动窗口中数值之和
        int min = nums.size() + 1;   //表示最小长度
        int len = 0;    //表示当前窗口长度
        for(int right = 0; right < nums.size(); right++){
            sum += nums[right];
            while(sum >= target){   //注意使用的是while，而不是if判断，while循环直到窗口值不符合条件后，将末尾指针向右移
                len = right - left + 1;
                if(len < min){
                    min = len;
                }
                sum -= nums[left++];   //精髓所在！不断将i向右移动，并且更新sum值           
            }
        }
        return min == nums.size() + 1 ? 0 : min;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
904. 水果成篮

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

这道题和上一道题（209）最大的不同就在于，上一道是在求最小窗口，而这一道在求最大窗口。

关键区别就在于：

最大窗口是在迭代右移右边界的过程中（while中）更新结果；

最小窗口是在迭代右移左边界的过程中（for中）更新结果。

解题思路：

由于tree[i] 的值表示水果的种类，所以可以使用map<int, int>来定义对应种类水果，对应个数。对应种类水果，又使用tree[i]来表示；

思路：

滑动窗口：两种类型水果的总数量

右边界：不断向右移动，并记录对应种类水果数量。直到遇到第三种水果（wimdow.size() > 2），比较记录是否是最大窗口，并且开始移动左边界，进行缩小窗口

左边界：记录第一个种类水果的最左边界，当遇到第三种水果时，左边界开始右移，直到有一种水果数量为零，此时窗口又变成两种水果，退出左边界缩小

参考代码：

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        unordered_map<int, int> window; //定义map存放对应种类水果个数
        int left = 0;
        int result = 0;     //表示最终最大窗口，也就是最多有几个水果
        for(int right = 0; right < fruits.size(); right++){
            window[fruits[right]]++;
            while(window.size() > 2){   //当第三种水果出现时，收缩窗口，寻找左边界
                window[fruits[left]]--;
                if(window[fruits[left]] == 0){ //有一种水果个数为零
                    window.erase(fruits[left]); //将这种水果删除
                }
                left++; //左边界右移，直到种类数又变成2
            }
            //注意，寻找最大窗口值时，是在while循环结束后，也就是右边界移动过程中，更新结果。
            result = max(result, right - left + 1);
        }
        return result;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
76. 最小覆盖子串

待解决

模拟行为

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

解题思路：

该题为模拟题，但容易越写越乱，最后修修改改思路混乱。

针对此类模拟题，要遵循循环不变量的原则，即对每条边都要坚持不变的处理规则。

这道题的循环不变量为：按照左闭右开的规则处理每一条边（即每条边的最后一个节点不处理，留给下一条边的起始位置）

  1. 循环转几圈？

    n/2—>最后判断if (n % 2 == 1) 如果是奇数，则需要将中心数字填充完整

  2. 循环中如何实现？

    • 每一圈的起始位置如何定义？

      不是每一圈起点都是（0,0），所以需要定义变量startx和starty，用来表示每一圈起始位置，并且每一圈循环后改变对应值（startx++, starty++ )，进行下一圈赋值。

    • 每条边的终止位置如何定义？

      定义一个变量offset，初始值为1，每一圈offset++；

    • 每条边如何赋值？

      使用for循环，搭配startx或starty以及终止条件（n-offset）进行依次赋值（count++）

  3. 如何定义一个二维数组？

    vector<vector<int> > res(row, vector<int>(column, 0));	//初始化row*column二维动态数组res，初始化值为0

    • 1

    解释：定义了一个vector容器，元素类型为vector，初始化为包含m个vector对象，每个对象都是一个新创立的vector对象的拷贝，而这个新创立的vector对象被初始化为包含n个0。
    vector(n)表示构造一个无名且含n个0的vector对象。

    这个讲解不错：https://ashleyzhao.blog.csdn.net/article/details/123821901?spm=1001.2101.3001.6650.3&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-3-123821901-blog-113831570.pc_relevant_multi_platform_whitelistv3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-3-123821901-blog-113831570.pc_relevant_multi_platform_whitelistv3&utm_relevant_index=6

参考代码：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int> > res(n, vector<int>(n, 0));  //使用vector，初始化一个n*n的二维数组res
        int loop = n / 2;   //表示需要转多少圈,控制循环次数，如果n为奇数的话，最后还需要另外赋值给中心位置。
        int startx = 0, starty = 0; //初始化循环一个圈的起始x，y坐标
        int count = 1;  //给矩阵中每个空格赋值
        int offset = 1; //终止条件，需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i, j;   //i，j为全局变量，方便赋值时使用
        while(loop--){  //控制循环圈数
            i = startx;
            j = starty;
            //4个for循环就是模拟一个圈
            // 模拟填充上行从左到右(左闭右开)
            for(j = starty; j < n - offset; j++)
                res[startx][j] = count++;
            //for循环后，此时j = n - offset，可用于后面定位

            // 模拟填充右列从上到下(左闭右开)
            for(i = startx; i < n - offset; i++)
                res[i][j] = count++;    //因为j是全局变量，所以此时j是一个固定的值
            //for循环后，此时i = n - offset，可用于后面定位

            // 模拟填充下行从右到左(左闭右开)
            for(; j > starty; j--)
                res[i][j] = count++;
            //for循环后，此时j = starty

            // 模拟填充左列从下到上(左闭右开)
            for(; i > startx; i--)
                res[i][j] = count++;
            //for循环后，此时x = startx

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;
            // offset 控制每一圈里每一条边遍历的长度
            offset++;
        }
        if(n % 2 == 1){ //如果n是奇数，需要给中心赋值
            res[n / 2][n / 2] = count;
        }
        return res;
    }
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45

总结

img

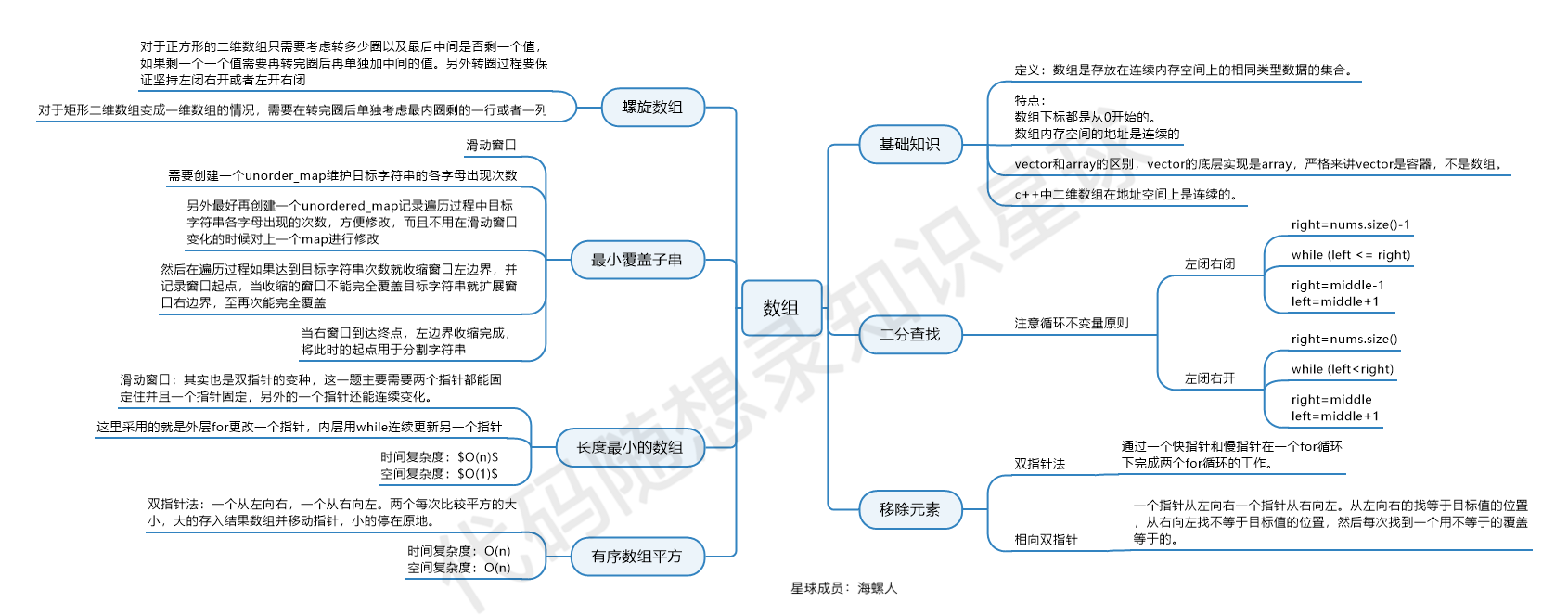
题型总结：

二分法

数组：每次遇到二分法，都是一看就会，一写就废(opens new window)

这道题目呢，考察数组的基本操作，思路很简单，但是通过率在简单题里并不高，不要轻敌。

可以使用暴力解法，通过这道题目，如果追求更优的算法，建议试一试用二分法，来解决这道题目

  • 暴力解法时间复杂度：O(n)
  • 二分法时间复杂度：O(logn)

在这道题目中我们讲到了循环不变量原则，只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。

二分法是算法面试中的常考题，建议通过这道题目，锻炼自己手撕二分的能力。

双指针法

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

  • 暴力解法时间复杂度：O(n^2)
  • 双指针时间复杂度：O(n)

这道题目迷惑了不少同学，纠结于数组中的元素为什么不能删除，主要是因为以下两点：

  • 数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）。
  • C++中vector和array的区别一定要弄清楚，vector的底层实现是array，封装后使用更友好。

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组和链表操作的面试题，都使用双指针法。

滑动窗口

本题介绍了数组操作中的另一个重要思想：滑动窗口。

  • 暴力解法时间复杂度：O(n^2)
  • 滑动窗口时间复杂度：O(n)

本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

模拟行为

模拟类的题目在数组中很常见，不涉及到什么算法，就是单纯的模拟，十分考察大家对代码的掌控能力。

在这道题目中，我们再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。

相信大家有遇到过这种情况： 感觉题目的边界调节超多，一波接着一波的判断，找边界，拆了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的，大家可以在这道题目中体会到这一点。

mmercarl.com/0704.二分查找.html)

这道题目呢，考察数组的基本操作，思路很简单，但是通过率在简单题里并不高，不要轻敌。

可以使用暴力解法，通过这道题目，如果追求更优的算法，建议试一试用二分法，来解决这道题目

  • 暴力解法时间复杂度：O(n)
  • 二分法时间复杂度：O(logn)

在这道题目中我们讲到了循环不变量原则，只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。

二分法是算法面试中的常考题，建议通过这道题目，锻炼自己手撕二分的能力。

双指针法

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

  • 暴力解法时间复杂度：O(n^2)
  • 双指针时间复杂度：O(n)

这道题目迷惑了不少同学，纠结于数组中的元素为什么不能删除，主要是因为以下两点：

  • 数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）。
  • C++中vector和array的区别一定要弄清楚，vector的底层实现是array，封装后使用更友好。

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组和链表操作的面试题，都使用双指针法。

滑动窗口

本题介绍了数组操作中的另一个重要思想：滑动窗口。

  • 暴力解法时间复杂度：O(n^2)
  • 滑动窗口时间复杂度：O(n)

本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

模拟行为

模拟类的题目在数组中很常见，不涉及到什么算法，就是单纯的模拟，十分考察大家对代码的掌控能力。

在这道题目中，我们再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。

相信大家有遇到过这种情况： 感觉题目的边界调节超多，一波接着一波的判断，找边界，拆了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的，大家可以在这道题目中体会到这一点。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/码创造者/article/detail/788869
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号