数据科学与机器学习管道中预处理的重要性（三）：缩放数据来抵抗噪声

原文链接：The importance of preprocessing in data science and the machine learning pipeline III: scaling your data to combat noise
作者：Hugo Bowne-Anderson
译者：刘翔宇 审校：赵屹华
责编：周建丁（zhoujd@csdn.net）
未经许可，请勿转载！

在前两篇文章中，我探索了在机器学习管道中预处理数据的作用。特别地，我检测了K近邻（k-NN）和逻辑回归算法，并看到缩放数值型数据对前者性能有很大影响，但对于后者并没有多大影响，我用精度作为参考（见下方的词汇列表或者前两篇文章，k-NN和其他相关词条）。你需要记住的是，预处理不是凭空产生的，你可以对数据进行处理，但下面是你处理数据的理由：在对数进行处理之后模型性能会怎样？

缩放数值型数据（即，将所有变量与一个常数相乘，来改变那个变量的范围）有两个相关用途：i）如果你的测量单位是米而我的是英里，那么，如果我们都缩放数据，它们最终是一样的。ii）如果两个变量的范围相差巨大，范围大的那个变量可能主导预测模型，即使它对目标变量的重要性不及那个小范围变量。在第二点中我们看到的现象会在k-NN中出现，在数据集都比较集中时尤为明显，但是逻辑回归中不会出现类似的现象，因为在训练逻辑回归模型时，会缩小相关系数来弥补缩放缺失。

在之前两篇文章中，我们使用的数据都是真实世界的数据，我们所能看到的是进行缩放前后，模型的性能情况。在这，我将使用滋扰变量（不会影响目标变量但会影响模型）形式的噪声来看看它会对缩放前后的模型有何影响，我将合成一个数据集，在此我可以控制滋扰变量的确切性质。我们将会看到，合成数据噪声越大，缩放对k-NN越重要。这里所有的样例代码都由Python编写。如果你不熟悉Python，你可以参考我们的DataCamp课程。我将使用pandas库来处理数据以及scikit-learn来进行机器学习。

在下面的代码块中，我们使用scikit-learn的make_blobs 函数生成2000个数据点，属于4个簇（每个数据点包含两个预测变量和一个目标变量）。

# Generate some clustered data (blobs!)
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
n_samples=2000
X, y = make_blobs(n_samples, centers=4, n_features=2,
                  random_state=0)
1
2
3
4
5
6

绘制合成数据

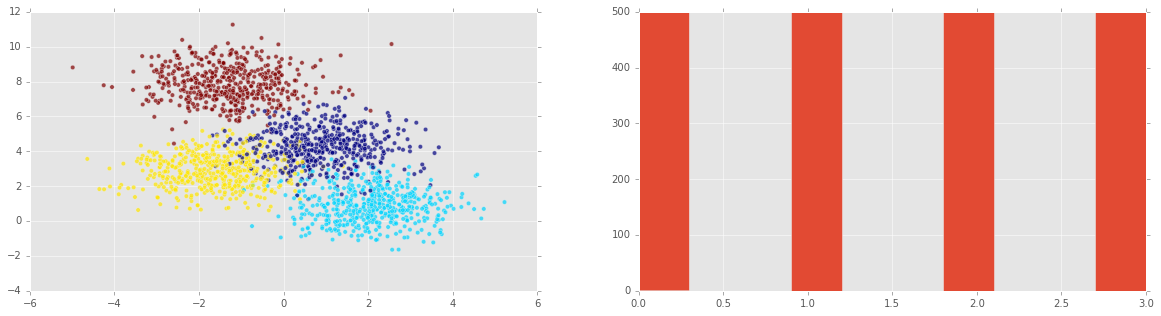
现在我们在平面上绘制合成的数据。每个轴是一个预测变量，数据点的颜色代表目标变量：

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.scatter(X[:,0] , X[:,1],  c = y, alpha = 0.7);
plt.subplot(1, 2, 2);
plt.hist(y)
plt.show()
1
2
3
4
5
6
7
8
9

注意：我们可以在第二幅图中看到所有可能的目标变量都均等。在这种情况下（或者它们大致均等），我们说类y是平衡的。

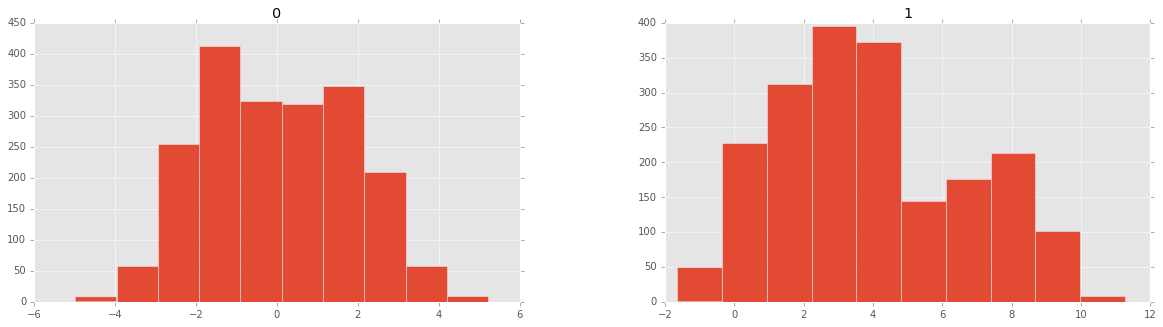
现在我来绘制特征（预测变量）直方图：

import pandas as pd
df = pd.DataFrame(X)
pd.DataFrame.hist(df, figsize=(20,5));
1
2
3

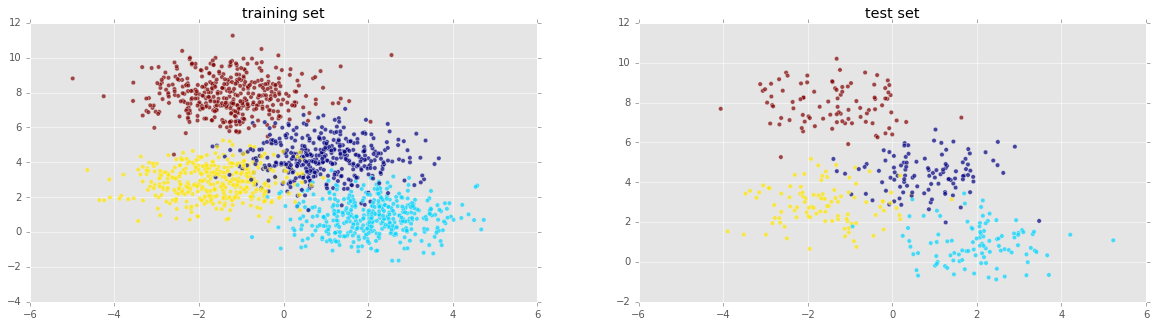
现在来分割测试集合训练集，然后把它们绘制出来：

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.title('training set')
plt.scatter(X_train[:,0] , X_train[:,1],  c = y_train, alpha = 0.7);
plt.subplot(1, 2, 2);
plt.scatter(X_test[:,0] , X_test[:,1],  c = y_test, alpha = 0.7);
plt.title('test set')
plt.show()
1
2
3
4
5
6
7
8
9
10

看起来还不错！现在我们来实例化一个K近邻投票分类器，然后在训练集上训练：

from sklearn import neighbors, linear_model
knn = neighbors.KNeighborsClassifier()
knn_model = knn.fit(X_train, y_train)
1
2
3

现在我们训练好了一个模型，我们可以用它来预测测试集并计算精度：

print('k-NN score for test set: %f' % knn_model.score(X_test, y_test))

k-NN score for test set: 0.935000
1
2
3

我们也可以再用这个模型拟合训练集并计算其精度，希望在训练集上比测试集表现更好：

print('k-NN score for training set: %f' % knn_model.score(X_train, y_train))
1

k-NN score for training set: 0.941875
1

值得重申，scikit-learn中k-NN默认的计分方法是精度。要查看其它指标，我们也可以使用scikit-learn的分类报告：

from sklearn.metrics import classification_report
y_true, y_pred = y_test, knn_model.predict(X_test)
print(classification_report(y_true, y_pred))
1
2
3

              precision    recall  f1-score   support

          0       0.87      0.90      0.88       106
          1       0.98      0.93      0.95       102
          2       0.90      0.92      0.91       100
          3       1.00      1.00      1.00        92

avg / total       0.94      0.94      0.94       400
1
2
3
4
5
6
7
8

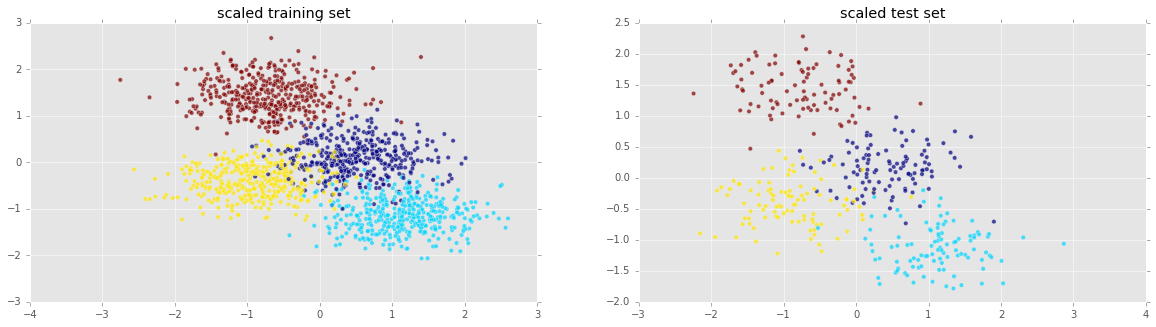
现在来缩放数据

现在我将缩放预测变量，然后再次使用k-NN：

from sklearn.preprocessing import scale
Xs = scale(X)
Xs_train, Xs_test, y_train, y_test = train_test_split(Xs, y, test_size=0.2, random_state=42)
plt.figure(figsize=(20,5));
plt.subplot(1, 2, 1 );
plt.scatter(Xs_train[:,0] , Xs_train[:,1],  c = y_train, alpha = 0.7);
plt.title('scaled training set')
plt.subplot(1, 2, 2);
plt.scatter(Xs_test[:,0] , Xs_test[:,1],  c = y_test, alpha = 0.7);
plt.title('scaled test set')
plt.show()
1
2
3
4
5
6
7
8
9
10
11

knn_model_s = knn.fit(Xs_train, y_train)
print('k-NN score for test set: %f' % knn_model_s.score(Xs_test, y_test))
1
2
3

k-NN score for test set: 0.935000
1

使用缩放对性能并没有任何改进！这大概是因为所有特征都处于同一范围内。当各种变量范围差别巨大时，缩放才有意义。想看看它的实际作用，我们将会加入另外一个特征。此外，该特征将与目标变量无关：这纯粹是噪声。

在信号中加入噪声：

我们加入高斯噪声变量，均值为0，变量标准差为 σ 。我们称 σ 为噪声强度，我们会看到，噪声强度越大，k近邻性能越差。

# Add noise column to predictor variables
ns = 10**(3) # Strength of noise term
newcol = np.transpose([ns*np.random.randn(n_samples)])
Xn = np.concatenate((X, newcol), axis = 1)
1
2
3
4

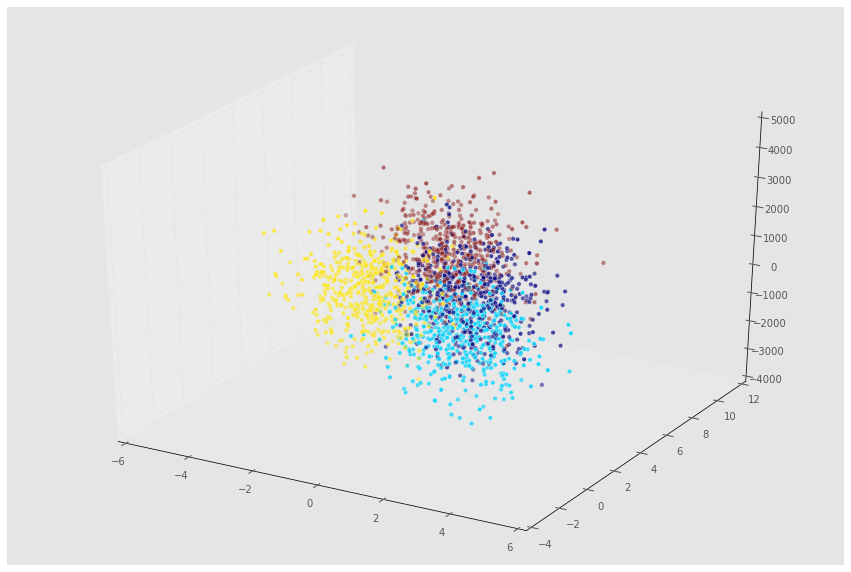
我们现在使用mplot3d包来绘制数据3D图：

from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(15,10));
ax = fig.add_subplot(111, projection='3d' , alpha = 0.5);
ax.scatter(Xn[:,0], Xn[:,1], Xn[:,2], c = y);
1
2
3
4

现在来看看模型在新数据上的表现如何：

Xn_train, Xn_test, y_train, y_test = train_test_split(Xn, y, test_size=0.2, random_state=42)
knn = neighbors.KNeighborsClassifier()
knn_model = knn.fit(Xn_train, y_train)
print('k-NN score for test set: %f' % knn_model.score(Xn_test, y_test))
1
2
3
4

k-NN score for test set: 0.400000
1

这个模型糟透了！不如我们缩放看看性能如何？

Xns = scale(Xn)
s = int(.2*n_samples)
Xns_train = Xns[s:]
y_train = y[s:]
Xns_test = Xns[:s]
y_test = y[:s]
knn = neighbors.KNeighborsClassifier()
knn_models = knn.fit(Xns_train, y_train)
print('k-NN score for test set: %f' % knn_models.score(Xns_test, y_test))
1
2
3
4
5
6
7
8
9

k-NN score for test set: 0.907500
1

太棒了，缩放数据之后，模型的性能与加入噪声之前差不多。现在我们使用噪声强度函数来看看模型性能的变化。

噪声越强，问题越大：

我们现在来看看噪声强度对模型精度的影响。因为我们需要多次使用相同代码，所以把主要部分封装成一个小函数：

def accu( X, y):
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
    knn = neighbors.KNeighborsClassifier()
    knn_model = knn.fit(X_train, y_train)
    return(knn_model.score(X_test, y_test))
1
2
3
4
5

noise = [10**i for i in np.arange(-1,6)]
A1 = np.zeros(len(noise))
A2 = np.zeros(len(noise))
count = 0
for ns in noise:
    newcol = np.transpose([ns*np.random.randn(n_samples)])
    Xn = np.concatenate((X, newcol), axis = 1)
    Xns = scale(Xn)
    A1[count] = accu( Xn, y)
    A2[count] = accu( Xns, y)
    count += 1
1
2
3
4
5
6
7
8
9
10
11

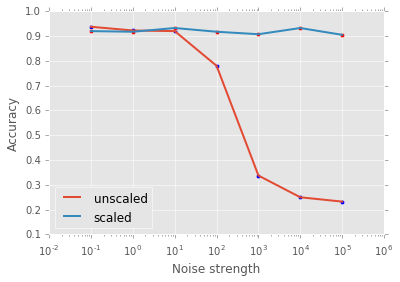
现在我们绘制噪声强度函数精度图（注意，x轴取对数）：

plt.scatter( noise, A1 )
plt.plot( noise, A1, label = 'unscaled', linewidth = 2)
plt.scatter( noise, A2 , c = 'r')
plt.plot( noise, A2 , label = 'scaled', linewidth = 2)
plt.xscale('log')
plt.xlabel('Noise strength')
plt.ylabel('Accuracy')
plt.legend(loc=3);
1
2
3
4
5
6
7
8

在上图中可以看出，滋扰变量中噪声越多，在k-NN模型中缩放数据就越重要！下面你将有机会对逻辑回归做此尝试。最后，我们已经看到预处理的缩放和中心化在数据科学管道中的重要地位，而且我们在机器学习挑战上这么做进行了一次整体研究。在将来的文章中，我希望将这个讨论扩展到其他类型的预处理，比如数值型数据的转换，类别数据的预处理，它们都是任何数据科学家工具箱中不可缺少的方面。

热心读者练习：使用逻辑回归模型拟合上面的合成数据，然后检查模型的性能。使用同样噪声强度函数，缩放和未缩放数据时的精度如何？你可以在下面的DataCamp Light窗口中实践！改变以10为底的指数范围来改变噪声量（先试试我在上面k-NN中使用的范围），然后设置sc=True来缩放特征。你同样可以在Github上检出DataCamp Light！

# Below, change the exponent of 10 to alter the amount of noise
ns = 10**(3) # Strength of noise term
# Set sc = True if you want to scale your features
sc = False

#Import packages
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn import neighbors, linear_model
from sklearn.preprocessing import scale
from sklearn.datasets.samples_generator import make_blobs

#Generate some data
n_samples=2000
X, y = make_blobs(n_samples, centers=4, n_features=2,
                 random_state=0)

# Add noise column to predictor variables
newcol = np.transpose([ns*np.random.randn(n_samples)])
Xn = np.concatenate((X, newcol), axis = 1)

#Scale if desired
if sc == True:
    Xn = scale(Xn)

#Train model and test after splitting
Xn_train, Xn_test, y_train, y_test = train_test_split(Xn, y, test_size=0.2, random_state=42)
lr = linear_model.LogisticRegression()
lr_model = lr.fit(Xn_train, y_train)
print('logistic regression score for test set: %f' % lr_model.score(Xn_test, y_test))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

<script.py> output:
    logistic regression score for test set: 0.935000

In [1]: 
1
2
3
4