阿里云安全恶意程序检测（速通一）_阿里云安全恶意程序检测数据集

赛题理解

赛题介绍

赛题说明

本题目提供的数据来自经过沙箱程序模拟运行后的API指令序列，全为Windows二进制可执行程序，经过脱敏处理:样本数据均来自互联网，其中恶意文件的类型有感染型病毒、木马程序、挖矿程序、DDoS 木马、勒索病毒等，数据总计6亿条。

注：什么是沙箱程序？
在计算机安全中，沙箱（Sandbox）是一种用于隔离正在运行程序的安全机制，通常用于执行未经测试或者不受信任的程序或代码，它会为待执行的程序创建一个独立的执行环境，内部程序的执行不会影响到外部程序的运行。

数据说明

评测指标

需特别注意，log 对于小于1的数是非常敏感的。比如log0.1和log0.000 001的单个样本的误差为10左右，而log0.99和log0.95的单个误差为0.1左右。

logloss和AUC的区别:AUC只在乎把正样本排到前面的能力，logloss更加注重评估的准确性。如果给预测值乘以一个倍数，则AUC不会变，但是logloss 会变。

赛题分析

数据特征

本赛题的特征主要是API接口的名称,这是融合时序与文本的数据，同时接口名称基本表达了接口用途。因此，最基本、最简单的特征思路是对所有API数据构造CountVectorizer特征。

说明: CountVectorizer 是属于常见的特征数值计算类，是一个文本特征提取方法。对于每一个训练文本，它只考虑每种词汇在该训练文本中出现的频率。

解题思路

本赛题根据官方提供的每个文件对API的调用顺序及线程的相关信息按文件进行分类，将文件属于每个类的概率作为最终的结果进行提交，并采用官方的logloss作为最终评分，属于典型的多分类问题。

数据探索

数据特征类型

train.info()
train.head(5)
train.describe()
1
2
3

数据分布

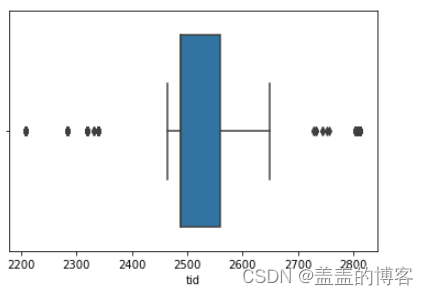
箱型图

#使用箱型图查看单个变量的分布情况。
#取前10000条数据绘制tid变量的箱型图
#os:当数据量太大时，变量可视化取一部分
sns.boxplot(x = train.iloc[:10000]["tid"])
1
2
3
4

变量取值分布

#用函数查看训练集中变量取值的分布
train.nunique()
1
2

缺失值

#查看缺失值
train.isnull().sum()
1
2

异常值

#异常值：分析训练集的index特征
train['index'].describe()
1
2

分析训练集的tid特征

#分析训练集的tid特征
train['tid'].describe()
1
2

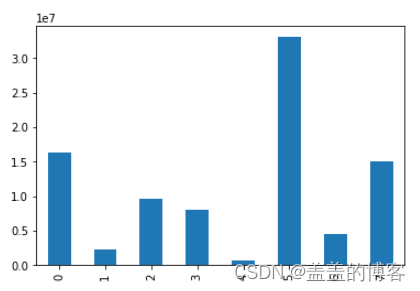
标签分布

#统计标签取值的分布情况
train['label'].value_counts()
1
2

直观化：

train['label'].value_counts().sort_index().plot(kind = 'bar')
1

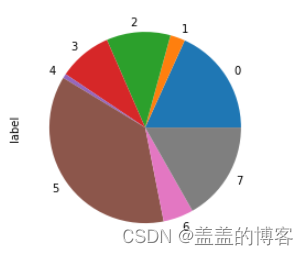
train['label'].value_counts().sort_index().plot(kind = 'pie')
1

测试集数据探索同上

数据集联合分析

file_id分析

#对比分析file_id变量在训练集和测试集中分布的重合情况：
train_fileids = train['file_id'].unique()
test_fileids = test['file_id'].unique()
len(set(train_fileids) - set(test_fileids))
1
2
3
4

API分析

#对比分析API变量在训练集和测试集中分布的重合情况
train_apis = train['api'].unique()
test_apis = test['api'].unique()
set(set(test_apis) - set(train_apis))
1
2
3
4

特征工程与基线模型

构造特征与特征选择

基于数据类型的方法

基于多分析视角的方法

这是最常见的一种特征构造方法，在所有的基于table 型(结构化数据)的比赛中都会用到。

我们以用户是否会在未来三天购买同一物品为例，来说明此类数据的构建角度:用户长期购物特征，用户长期购物频率;用户短期购物特征，用户近期购物频率;物品受欢迎程度，该物品最近受欢迎程度;

用户对此类产品的喜好特征:用户之前购买该类/该商品的频率等信息;

时间特征:是否到用户发工资的时间段:商品是否为用户的必备品，如洗漱用品、每隔多长时间必买等。

特征选择

特征选择主要包含过滤法、包装法和嵌入法三种，前面已经介绍过。

构造线下验证集

在数据竞赛中，为了防止选手过度刷分和作弊，每日的线上提交往往是有次数限制的。因此，线下验证集的构造成为检验特征工程、模型是否有效的关键。在构造线下验证集时，我们需要考虑以下几个方面的问题。

评估穿越

评估穿越最常见的形式是时间穿越和会话穿越两种。

1.时间穿越

例1: 假设我们需要预测用户是否会去观看视频B，在测试集中需要预测用户8月8日上午10:10点击观看视频B的概率，但是在训练集中已经发现该用户8月8日上午10:09在观看视频A,上午10:11 也在观看视频A,那么很明显该用户就有非常大的概率不看视频B,通过未来的信息很容易就得出了该判断。

例2: 假设我们需要预测用户9月10日银行卡的消费金额，但是在训练集中已经出现了该用户银行卡的余额在9月9日和9月11日都为0，那么我们就很容易知道该用户在9月10日的消费金额是0，出现了时间穿越的消息。

2.会话穿越

以电商网站的推荐为例，当用户在浏览某一个商品时，某个推荐模块会为他推荐多个商品进行展现，用户可能会点击其中的一个或几个。为了描述方便，我们将这些一 次展现中产生的，点击和未点击的数据合起来称为一 次会话(不同于计算机网络中会话的概念)。在上面描述的样本划分方法中，一次会话中的样本可能有一部分被划分到训练集，另一部分被划分到测试集。这样的行为，我们称之为会话穿越。

会话穿越的问题在于，由于一个会话对应的是
一个用户在一次展现中的行为，因此存在较高的相关性，穿越会带来类似上面提到的用练习题考试的问题。此外，会话本身是不可分割的，也就是说，在线上使用模型时，不可能让你先看到一次会话的一部分，然后让你预测剩余的部分，因为会话的展现结果是一次性产生的，一旦产生后，模型就已经无法干预展现的结果了。

3.穿越本质

穿越本质上是信息泄露的问题。无论时间穿越，还是会话穿越，其核心问题都是训练数据中的信息以不同方式、不同程度泄露到了测试数据中。.

训练集和测试集的特征性差异

我们用训练集训练模型，当训练集和测试集的特征分布有差异时，就容易造成模型偏差，导致预测不准确。常见的训练集和测试集的特征差异如下:

数值特征:训练集和测试集的特征分布交叉部分极小；

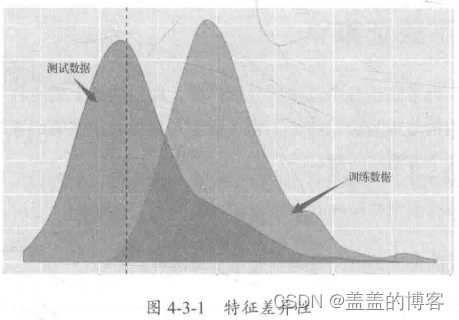
类别特征:测试集中的特征大量未出现在训练集中。例如，在微软的一场比赛中，测试集中的很多版本未出现在训练集中。

在某些极端情况下，训练集中极强的特征会在测试集中全部缺失。

训练集和测试集是分布差异性

训练集和测试集的分布差异性的判断步骤如下:
将训练集的数据标记为label=1,将测试集的数据标记为label= 0。对训练集和测试集做5折的auc交叉验证。如果auc在0.5附近，那么则说明训练集和测试集的分布差异不大:如果auc在0.9附近，那么则说明训练集和测试集的分布差异很大。

基线模型

导包 -> 读取数据 -> 特征工程

特征工程

·利用count（）函数和nunique（）函数生成特征：反应样本调用api,tid,index的频率信息

def simple_sts_features(df):
    simple_fea = pd.DataFrame()
    simple_fea['file_id'] = df['file_id'].unique()
    simple_fea = simple_fea.sort_values('file_id')
    
    df_grp = df.groupby('file_id')
    simple_fea['file_id_api_count'] = df_grp['api'].count().values
    simple_fea['file_id_api_nunique'] = df_grp['api'].nunique().values
    
    simple_fea['file_id_tid_count'] = df_grp['tid'].count().values
    simple_fea['file_id_tid_nunique'] = df_grp['tid'].nunique().values
    
    simple_fea['file_id_index_count'] = df_grp['index'].count().values
    simple_fea['file_id_index_nunique'] = df_grp['index'].nunique().values
    
    return simple_fea
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

·利用main（），min(),std(),max()函数生成特征：tid,index可认为是数值特征，可提取对应的统计特征。

def simple_numerical_sts_features(df):
    simple_numerical_fea = pd.DataFrame()
    simple_numerical_fea['file_id'] = df['file_id'].unique()
    simple_numerical_fea = simple_numerical_fea.sort_values('file_id')
    
    df_grp = df.groupby('file_id')
    
    simple_numerical_fea['file_id_tid_mean'] = df_grp['tid'].mean().values
    simple_numerical_fea['file_id_tid_min'] = df_grp['tid'].min().values
    simple_numerical_fea['file_id_tid_std'] = df_grp['tid'].std().values
    simple_numerical_fea['file_id_tid_max'] = df_grp['tid'].max().values
    
    simple_numerical_fea['file_id_index_mean'] = df_grp['index'].mean().values
    simple_numerical_fea['file_id_index_min'] = df_grp['index'].min().values
    simple_numerical_fea['file_id_index_std'] = df_grp['index'].std().values
    simple_numerical_fea['file_id_index_max'] = df_grp['index'].max().values
    
    return simple_numerical_fea
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

·利用定义的特征生成函数，并生成训练集和测试集的统计特征。

%%time
#统计api,tid,index的频率信息的特征统计
simple_train_fea1 = simple_sts_features(train)
%%time
simple_test_fea1 = simple_sts_features(test)
1
2
3
4
5

%%time
#统计tid,index等数值特征的特征统计
simple_train_fea2 = simple_numerical_sts_features(train)
%%time
simple_test_fea2 = simple_numerical_sts_features(test)
1
2
3
4
5

基线构建

获取标签：

#获取标签
train_label = train[['file_id','label']].drop_duplicates(subset=['file_id','label'],keep='first')
test_submit = test[['file_id']].drop_duplicates(subset=['file_id'],keep='first')
1
2
3

训练集和测试集的构建：

#训练集和测试集的构建
train_data = train_label.merge(simple_train_fea1,on = 'file_id',how = 'left')
train_data = train_data.merge(simple_train_fea2,on = 'file_id',how = 'left')

test_submit = test_submit.merge(simple_test_fea1,on = 'file_id',how = 'left')
test_submit = test_submit.merge(simple_test_fea2,on = 'file_id',how = 'left')
1
2
3
4
5
6

因为本赛题给出的指标和传统的指标略有不同，所以需要自己写评估指标，这样方便对比线下与线上的差距，以判断是否过拟合、是否出现线上线下不一致的问题等。

#关于LGB的自定义评估指标的书写
def lgb_logloss(preds,data):
    labels_ = data.get_label()
    classes_ = np.unique(labels_)
    preds_prob = []
    for i in range(len(classes_)):
        preds_prob.append(preds[i * len(labels_):(i+1)*len(labels_)])
        
    preds_prob_ = np.vstack(preds_prob)
    
    loss = []
    for i in range(preds_prob_.shape[1]):  #样本个数
        sum_ = 0
        for j in range(preds_prob_.shape[0]):  #类别个数
            pred = preds_prob_[j,i]  #第i个样本预测为第j类的概率
            if j == labels_[i]:
                sum_ += np.log(pred)
            else:
                sum_ += np.log(1 - pred)
        loss.append(sum_)
        return 'loss is: ',-1 * (np.sum(loss) / preds_prob_.shape[1]),False

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

线下验证：

train_features = [col for col in train_data.columns if col not in ['label','file_id']]
train_label = 'label'
1
2

使用5折交叉验证，采用LGB模型：

%%time


from sklearn.model_selection import StratifiedKFold,KFold
params = {
    'task':'train',
    'num_leaves':255,
    'objective':'multiclass',
    'num_class':8,
    'min_data_in_leaf':50,
    'learning_rate':0.05,
    'feature_fraction':0.85,
    'bagging_fraction':0.85,
    'bagging_freq':5,
    'max_bin':128,
    'random_state':100
}

folds = KFold(n_splits=5,shuffle=True,random_state = 15)  #n_splits = 5定义5折
oof = np.zeros(len(train))

predict_res = 0
models = []
for fold_, (trn_idx,val_idx) in enumerate(folds.split(train_data)):
    print("fold n°{}".format(fold_))
    trn_data = lgb.Dataset(train_data.iloc[trn_idx][train_features],label = train_data.iloc[trn_idx][train_label].values)
    val_data = lgb.Dataset(train_data.iloc[val_idx][train_features],label = train_data.iloc[val_idx][train_label].values)
    
    clf = lgb.train(params,
                   trn_data,
                   num_boost_round = 2000,
                   valid_sets = [trn_data,val_data],
                   verbose_eval = 50,
                   early_stopping_rounds = 100,
                   feval = lgb_logloss)
    models.append(clf)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

特征重要性分析

#特征重要性分析
feature_importance = pd.DataFrame()
feature_importance['fea_name'] = train_features
feature_importance['fea_imp'] = clf.feature_importance()
feature_importance = feature_importance.sort_values('fea_imp',ascending = False)
plt.figure(figsize = [20,10,])
sns.barplot(x = feature_importance['fea_name'],y = feature_importance['fea_imp'])
1
2
3
4
5
6
7

由运行结果可以看出:

(1) API的调用次数和API的调用类别数是最重要的两个特征，即不同的病毒常常会调用不同的API，而且由于有些病毒需要复制自身的原因，因此调用API的次数会明显比其他不同类别的病毒多。

(2)第三到第五强的都是线程统计特征，这也较为容易理解，因为木马等病毒经常需要通过线程监听一些内容，所以在线程等使用上会表现的略有不同。

模型测试

#模型测试
pred_res = 0
fold = 5
for model in models:
    pred_res += model.predict(test_submit[train_features]) * 1.0 /fold
test_submit['prob0'] = 0
test_submit['prob1'] = 0
...
test_submit[['prob0','prob1','prob2','prob3','prob4','prob5','prob6','prob7']] = pred_res
test_submit[['file_id','prob0','prob1','prob2','prob3','prob4','prob5','prob6','prob7']].to_csv('baseline.csv',index = None)
1
2
3
4
5
6
7
8
9
10