布隆过滤器详解_什么是布隆过滤器

什么是布隆过滤器

布隆过滤器（Bloom Filter）是 1970 年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。主要用于判断一个元素是否在一个集合中。

通常我们会遇到很多要判断一个元素是否在某个集合中的业务场景，一般想到的是将集合中所有元素保存起来，然后通过比较确定。链表、树、散列表（又叫哈希表，Hash table）等等数据结构都是这种思路。但是随着集合中元素的增加，我们需要的存储空间也会呈现线性增长，最终达到瓶颈。同时检索速度也越来越慢，上述三种结构的检索时间复杂度分别为$O(n)$，$O(logn)$，$O(1)$。

这个时候，布隆过滤器（Bloom Filter）就应运而生。

布隆过滤器原理

布隆过滤器是由一个固定大小的二进制向量或者位图（bitmap）和一系列映射函数组成的。在初始状态时，对于长度为 m 的位数组，它的所有位都被置为0，如下图所示：

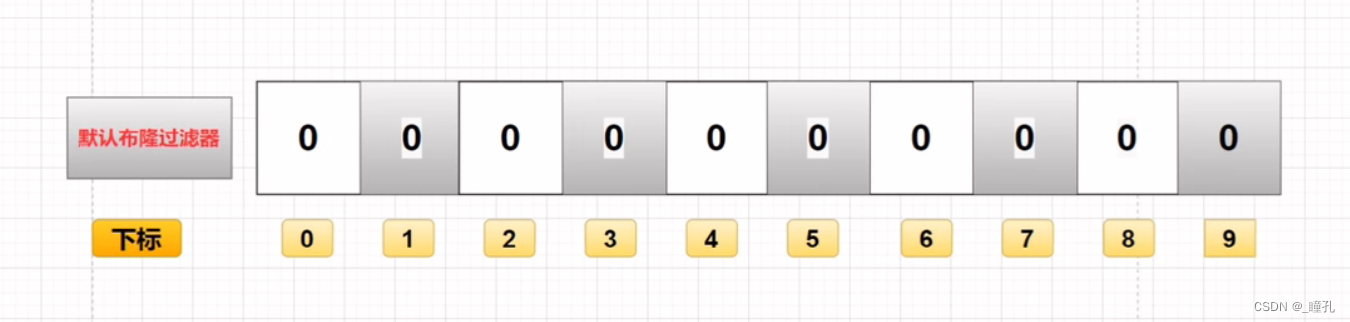
当有变量被加入集合时，通过 K 个映射函数将这个变量映射成位图中的 K 个点，把它们置为 1。

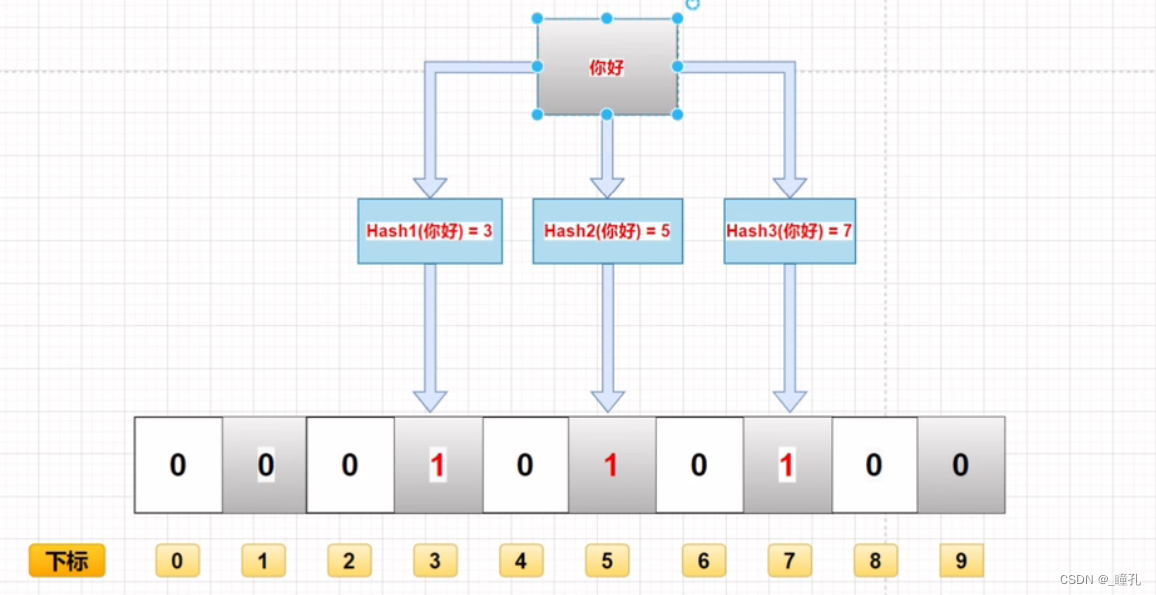
查询某个变量的时候我们只要看看这些点是不是都是 1 就可以大概率知道集合中有没有它了

• 如果这些点有任何一个 0，则被查询变量一定不在；
• 如果都是 1，则被查询变量很可能存在。为什么说是可能存在，而不是一定存在呢？那是因为映射函数本身就是散列函数，散列函数是会有碰撞的。

误判率：布隆过滤器的误判是指多个输入经过哈希之后在相同的bit位置1了，这样就无法判断究竟是哪个输入产生的，因此误判的根源在于相同的 bit 位被多次映射且置 1。这种情况也造成了布隆过滤器的删除问题，因为布隆过滤器的每一个 bit 并不是独占的，很有可能多个元素共享了某一位。如果我们直接删除这一位的话，会影响其他的元素。

特性：

• 一个元素如果判断结果为存在的时候元素不一定存在，但是判断结果为不存在的时候则一定不存在。
• 布隆过滤器可以添加元素，但是不能删除元素。因为删掉元素会导致误判率增加。

添加元素步骤：

• 将要添加的元素给 k 个哈希函数
• 得到对应于位数组上的 k 个位置
• 将这k个位置设为 1

查询元素步骤：

• 将要查询的元素给k个哈希函数
• 得到对应于位数组上的k个位置
• 如果k个位置有一个为 0，则肯定不在集合中
• 如果k个位置全部为 1，则可能在集合中‘

优点：相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数 $O(K)$，另外，散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。且布隆过滤器可以表示全集，其它任何数据结构都不能；

缺点：布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。另外，一般情况下不能从布隆过滤器中删除元素。我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加 1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面。这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。在降低误算率方面，有不少工作，使得出现了很多布隆过滤器的变种。

布隆过滤器使用场景

在程序的世界中，布隆过滤器是程序员的一把利器，利用它可以快速地解决项目中一些比较棘手的问题。

如网页 URL 去重、垃圾邮件识别、大集合中重复元素的判断和缓存穿透等问题。

布隆过滤器的典型应用有：

• 数据库防止穿库。 Google Bigtable，HBase 和 Cassandra 以及 Postgresql 使用BloomFilter来减少不存在的行或列的磁盘查找。避免代价高昂的磁盘查找会大大提高数据库查询操作的性能。
• 业务场景中判断用户是否阅读过某视频或文章，比如抖音或头条，当然会导致一定的误判，但不会让用户看到重复的内容。
• 缓存宕机、缓存击穿场景，一般判断用户是否在缓存中，如果在则直接返回结果，不在则查询db，如果来一波冷数据，会导致缓存大量击穿，造成雪崩效应，这时候可以用布隆过滤器当缓存的索引，只有在布隆过滤器中，才去查询缓存，如果没查询到，则穿透到db。如果不在布隆器中，则直接返回。
• WEB拦截器，如果相同请求则拦截，防止重复被攻击。用户第一次请求，将请求参数放入布隆过滤器中，当第二次请求时，先判断请求参数是否被布隆过滤器命中。可以提高缓存命中率。Squid 网页代理缓存服务器在 cache digests 中就使用了布隆过滤器。Google Chrome浏览器使用了布隆过滤器加速安全浏览服务。
• Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据。
• SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。

布隆过滤器的使用

google的Guava工具类已经做好了封装，可以直接使用：

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>23.0</version>
</dependency>
1
2
3
4
5

代码如下：

package com.eyes.base.test;

import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnels;

public class BloomFilterCase {
    // 预计插入数据
    private static int size = 1000000;


    // 期望的误判率
    private static double fpp = 0.01;

    // 布隆过滤器
    private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);

    private static int total = 1000000;

    public static void main(String[] args) {
        // 插入100w样本数据
        for (int i = 0; i < total; i++) {
            bloomFilter.put(i);
        }

        // 用另外10w测试数据，测试误判率
        int count = 0;
        for (int i = total; i < total + 100000; i++) {
            if(bloomFilter.mightContain(i)) {
                count++;
            }
        }
        System.out.println("总共误判数：" + count);
        System.out.println("误判率：" + (1.0 * count / 100000));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

自定义简易布隆过滤器

public class MyBloomFilter {

    /**
     * 一个长度为10 亿的比特位
     */
    private static final int DEFAULT_SIZE = 256 << 22;

    /**
     * 为了降低错误率，使用加法hash算法，所以定义一个8个元素的质数数组
     */
    private static final int[] seeds = {3, 5, 7, 11, 13, 31, 37, 61};

    /**
     * 相当于构建 8 个不同的hash算法
     */
    private static HashFunction[] functions = new HashFunction[seeds.length];

    /**
     * 初始化布隆过滤器的 bitmap
     */
    private static BitSet bitset = new BitSet(DEFAULT_SIZE);

    /**
     * 添加数据
     *
     * @param value 需要加入的值
     */
    public static void add(String value) {
        if (value != null) {
            for (HashFunction f : functions) {
                //计算 hash 值并修改 bitmap 中相应位置为 true
                bitset.set(f.hash(value), true);
            }
        }
    }

    /**
     * 判断相应元素是否存在
     * @param value 需要判断的元素
     * @return 结果
     */
    public static boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (HashFunction f : functions) {
            ret = bitset.get(f.hash(value));
            //一个 hash 函数返回 false 则跳出循环
            if (!ret) {
                break;
            }
        }
        return ret;
    }

    /**
     * 模拟用户是不是会员，或用户在不在线。。。
     */
    public static void main(String[] args) {

        for (int i = 0; i < seeds.length; i++) {
            functions[i] = new HashFunction(DEFAULT_SIZE, seeds[i]);
        }

        // 添加1亿数据
        for (int i = 0; i < 100000000; i++) {
            add(String.valueOf(i));
        }
        String id = "123456789";
        add(id);

        System.out.println(contains(id));   // true
        System.out.println("" + contains("234567890"));  //false
    }
}

class HashFunction {

    private int size;
    private int seed;

    public HashFunction(int size, int seed) {
        this.size = size;
        this.seed = seed;
    }

    public int hash(String value) {
        int result = 0;
        int len = value.length();
        for (int i = 0; i < len; i++) {
            result = seed * result + value.charAt(i);
        }
        int r = (size - 1) & result;
        return (size - 1) & result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

拓展

为了解决布隆过滤器不能删除元素的问题，布谷鸟过滤器横空出世。布谷鸟过滤器用更低的空间开销解决了布隆过滤器不能删除元素的问题，做到了更好的效果：

• 支持动态的添加和删除元素
• 提供了比传统布隆过滤器更高的查找性能，即使在接近满的情况下（比如空间利用率达到 95% 的时候）
• 比起商过滤器它更容易实现
• 如果要求误判率低于3%，它比布隆过滤器有更低的空间开销

相比布谷鸟过滤器而言布隆过滤器有以下不足：查询性能弱、空间利用效率低、不支持反向操作（删除）以及不支持计数，具体如下：

• 删除不完美，存在误删的概率。删除的时候知识删除了一份指纹副本，并不能确定此指纹副本是要删除的key的指纹。同时这个问题也导致了假阳性的情况。
• 插入复杂度比较高。随着插入元素的增多，复杂度会越来越高，因为存在桶满，踢出的操作，所以需要重新计算，但综合来讲复杂度还是常数级别。
• 存储空间的大小必须为2的指数的限制让空间效率打了折扣。
• 同一个元素最多插入kb次，（k指哈希函数的个数，b指的桶中能装指纹的个数也可以说是桶的尺寸大小）如果布谷鸟过滤器支持删除，则必须存储同一项的多个副本。 插入同一项kb+1次将导致插入失败。 这类似于计数布隆过滤器，其中重复插入会导致计数器溢出。

如果有兴趣了解更多相关内容，欢迎来我的个人网站看看：瞳孔的个人空间