【十大经典数据挖掘算法】系列_盘点数据挖掘十大经典算法案例

转自http://www.cnblogs.com/en-heng/p/5013995.html

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 决策树模型与学习

决策树（decision tree）算法基于特征属性进行分类，其主要的优点：模型具有可读性，计算量小，分类速度快。决策树算法包括了由Quinlan提出的ID3与C4.5，Breiman等提出的CART。其中，C4.5是基于ID3的，对分裂属性的目标函数做出了改进。

决策树模型

决策树是一种通过对特征属性的分类对样本进行分类的树形结构，包括有向边与三类节点：

• 根节点（root node），表示第一个特征属性，只有出边没有入边；
• 内部节点（internal node），表示特征属性，有一条入边至少两条出边
• 叶子节点（leaf node），表示类别，只有一条入边没有出边。

上图给出了（二叉）决策树的示例。决策树具有以下特点：

• 对于二叉决策树而言，可以看作是if-then规则集合，由决策树的根节点到叶子节点对应于一条分类规则;
• 分类规则是互斥并且完备的，所谓互斥即每一条样本记录不会同时匹配上两条分类规则，所谓完备即每条样本记录都在决策树中都能匹配上一条规则。
• 分类的本质是对特征空间的划分，如下图所示，

决策树学习

决策树学习的本质是从训练数据集中归纳出一组分类规则[2]。但随着分裂属性次序的不同，所得到的决策树也会不同。如何得到一棵决策树既对训练数据有较好的拟合，又对未知数据有很好的预测呢？

首先，我们要解决两个问题：

• 如何选择较优的特征属性进行分裂？每一次特征属性的分裂，相当于对训练数据集进行再划分，对应于一次决策树的生长。ID3算法定义了目标函数来进行特征选择。
• 什么时候应该停止分裂？有两种自然情况应该停止分裂，一是该节点对应的所有样本记录均属于同一类别，二是该节点对应的所有样本的特征属性值均相等。但除此之外，是不是还应该其他情况停止分裂呢？

2. 决策树算法

特征选择

特征选择指选择最大化所定义目标函数的特征。下面给出如下三种特征（Gender, Car Type, Customer ID）分裂的例子：

图中有两类类别（C0, C1），C0: 6是对C0类别的计数。直观上，应选择Car Type特征进行分裂，因为其类别的分布概率具有更大的倾斜程度，类别不确定程度更小。

为了衡量类别分布概率的倾斜程度，定义决策树节点的不纯度（impurity），其满足：不纯度越小，则类别的分布概率越倾斜；下面给出不纯度的的三种度量：

其中，表示对于决策树节点类别的概率。这三种不纯度的度量是等价的，在等概率分布是达到最大值。

为了判断分裂前后节点不纯度的变化情况，目标函数定义为信息增益（information gain）：

对应于决策树节点的不纯度，表示分裂前的父节点，表示父节点所包含的样本记录数，表示父节点分裂后的某子节点，为其计数，为分裂后的子节点数。

特别地，ID3算法选取熵值作为不纯度的度量，则

指父节点对应所有样本记录的类别；表示选择的特征属性，即的集合。那么，决策树学习中的信息增益等价于训练数据集中类与特征的互信息，表示由于得知特征的信息训练数据集不确定性减少的程度。

在特征分裂后，有些子节点的记录数可能偏少，以至于影响分类结果。为了解决这个问题，CART算法提出了只进行特征的二元分裂，即决策树是一棵二叉树；C4.5算法改进分裂目标函数，用信息增益比（information gain ratio）来选择特征：

因而，特征选择的过程等同于计算每个特征的信息增益，选择最大信息增益的特征进行分裂。此即回答前面所提出的第一个问题（选择较优特征）。ID3算法设定一阈值，当最大信息增益小于阈值时，认为没有找到有较优分类能力的特征，没有往下继续分裂的必要。根据最大表决原则，将最多计数的类别作为此叶子节点。即回答前面所提出的第二个问题（停止分裂条件）。

决策树生成

ID3算法的核心是根据信息增益最大的准则，递归地构造决策树；算法流程如下：

1. 如果节点满足停止分裂条件（所有记录属同一类别 or 最大信息增益小于阈值），将其置为叶子节点；
2. 选择信息增益最大的特征进行分裂；
3. 重复步骤1-2，直至分类完成。

C4.5算法流程与ID3相类似，只不过将信息增益改为信息增益比。

3. 决策树剪枝

过拟合

生成的决策树对训练数据会有很好的分类效果，却可能对未知数据的预测不准确，即决策树模型发生过拟合（overfitting）——训练误差（training error）很小、泛化误差（generalization error，亦可看作为test error）较大。下图给出训练误差、测试误差（test error）随决策树节点数的变化情况：

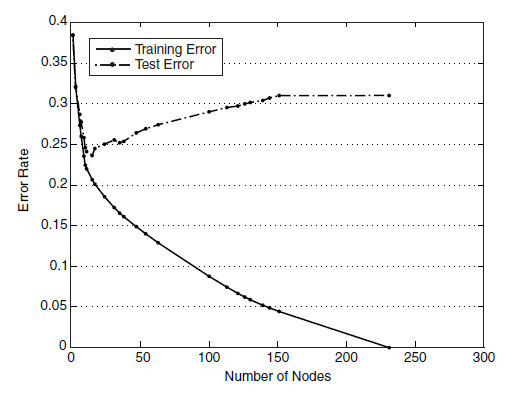
可以观察到，当节点数较小时，训练误差与测试误差均较大，即发生了欠拟合（underfitting）。当节点数较大时，训练误差较小，测试误差却很大，即发生了过拟合。只有当节点数适中是，训练误差居中，测试误差较小；对训练数据有较好的拟合，同时对未知数据有很好的分类准确率。

发生过拟合的根本原因是分类模型过于复杂，可能的原因如下：

• 训练数据集中有噪音样本点，对训练数据拟合的同时也对噪音进行拟合，从而影响了分类的效果；
• 决策树的叶子节点中缺乏有分类价值的样本记录，也就是说此叶子节点应被剪掉。

剪枝策略

为了解决过拟合，C4.5通过剪枝以减少模型的复杂度。[2]中提出一种简单剪枝策略，通过极小化决策树的整体损失函数（loss function）或代价函数（cost function）来实现，决策树的损失函数为：

其中，表示决策树的训练误差，为调节参数，为模型的复杂度。当模型越复杂时，训练的误差就越小。上述定义的损失正好做了两者之间的权衡。

如果剪枝后损失函数减少了，即说明这是有效剪枝。具体剪枝算法可以由动态规划等来实现。

4. 参考资料

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
[2] 李航，《统计学习方法》.
[3] Naren Ramakrishnan, The Top Ten Algorithms in Data Mining.