
package com.test.java.util;
 
/**
 * 坐标位置相关util
 */
public class PositionUtil {
 
    /**
     * 赤道半径（单位：米）
     */
    private static final double EQUATOR_RADIUS = 6378137;
 
    /**
     * 方法一：（反余弦计算方式）
     *
     * @param longitude1 第一个点的经度
     * @param latitude1  第一个点的纬度
     * @param longitude2 第二个点的经度
     * @param latitude2  第二个点的纬度
     * @return 返回距离，单位m
     */
    public static double getDistance1(double longitude1, double latitude1, double longitude2, double latitude2) {
        // 纬度
        double lat1 = Math.toRadians(latitude1);
        double lat2 = Math.toRadians(latitude2);
        // 经度
        double lon1 = Math.toRadians(longitude1);
        double lon2 = Math.toRadians(longitude2);
        // 纬度之差
        double a = lat1 - lat2;
        // 经度之差
        double b = lon1 - lon2;
        // 计算两点距离的公式
        double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(lat1) * Math.cos(lat2) * Math.pow(Math.sin(b / 2), 2)));
        // 弧长乘赤道半径, 返回单位: 米
        s = s * EQUATOR_RADIUS;
        return s;
    }
 
}

2.方法二


package com.test.java.util;
 
/**
 * 坐标位置相关util
 */
public class PositionUtil {
 
    /**
     * 地球平均半径（单位：米）
     */
    private static final double EARTH_AVG_RADIUS = 6371000;
    
    /**
     * 方法二：（反余弦计算方式）
     *
     * @param longitude1 第一点的经度
     * @param latitude1  第一点的纬度
     * @param longitude2 第二点的经度
     * @param latitude2  第二点的纬度
     * @return 返回的距离，单位m
     */
    public static double getDistance3(double longitude1, double latitude1, double longitude2, double latitude2) {
        // 经纬度（角度）转弧度。弧度作为作参数，用以调用Math.cos和Math.sin
        // A经弧度
        double radiansAX = Math.toRadians(longitude1);
        // A纬弧度
        double radiansAY = Math.toRadians(latitude1);
        // B经弧度
        double radiansBX = Math.toRadians(longitude2);
        // B纬弧度
        double radiansBY = Math.toRadians(latitude2);
 
        // 公式中“cosβ1cosβ2cos（α1-α2）+sinβ1sinβ2”的部分，得到∠AOB的cos值
        double cos = Math.cos(radiansAY) * Math.cos(radiansBY) * Math.cos(radiansAX - radiansBX) + Math.sin(radiansAY) * Math.sin(radiansBY);
        // System.out.println("cos = " + cos); // 值域[-1,1]
 
        // 反余弦值
        double acos = Math.acos(cos);
        // System.out.println("acos = " + acos); // 值域[0,π]
        // System.out.println("∠AOB = " + Math.toDegrees(acos)); // 球心角 值域[0,180]
 
        // 最终结果
        return EARTH_AVG_RADIUS * acos;
    }
 
}

3.方法三

基于谷歌地图的计算公式计算距离


package com.test.java.util;
 
/**
 * 坐标位置相关util
 */
public class PositionUtil {
 
    /**
     * 地球平均半径（单位：米）
     */
    private static final double EARTH_AVG_RADIUS = 6371000;
 
    /**
     * 经纬度转化为弧度(rad)
     *
     * @param d 经度/纬度
     */
    private static double rad(double d) {
        return d * Math.PI / 180.0;
    }
 
    /**
     * 方法三：（基于googleMap中的算法得到两经纬度之间的距离,计算精度与谷歌地图的距离精度差不多。）
     *
     * @param longitude1 第一点的经度
     * @param latitude1  第一点的纬度
     * @param longitude2 第二点的经度
     * @param latitude2  第二点的纬度
     * @return 返回的距离，单位m
     */
    public static double getDistance2(double longitude1, double latitude1, double longitude2, double latitude2) {
        double radLat1 = rad(latitude1);
        double radLat2 = rad(latitude2);
        double a = radLat1 - radLat2;
        double b = rad(longitude1) - rad(longitude2);
        double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(radLat1) * Math.cos(radLat2) * Math.pow(Math.sin(b / 2), 2)));
        s = s * EARTH_AVG_RADIUS;
        s = Math.round(s * 10000d) / 10000d;
        return s;
    }
 
}

4.方法四

基于高德地图


package com.test.java.util;
 
/**
 * 计算距离
 */
public class PositionUtil {
 
 
    /**
     * 方法四：（高德地图计算方法）
     *
     * @param longitude1 第一点的经度
     * @param latitude1  第一点的纬度
     * @param longitude2 第二点的经度
     * @param latitude2  第二点的纬度
     * @return 返回的距离，单位m
     */
    public static Double getDistance4(double longitude1, double latitude1, double longitude2, double latitude2) {
        if (longitude1 == 0 || latitude1 == 0 || latitude2 == 0 || longitude2 == 0) {
            return -1.0;
        }
        longitude1 *= 0.01745329251994329;
        latitude1 *= 0.01745329251994329;
        longitude2 *= 0.01745329251994329;
        latitude2 *= 0.01745329251994329;
        double var1 = Math.sin(longitude1);
        double var2 = Math.sin(latitude1);
        double var3 = Math.cos(longitude1);
        double var4 = Math.cos(latitude1);
        double var5 = Math.sin(longitude2);
        double var6 = Math.sin(latitude2);
        double var7 = Math.cos(longitude2);
        double var8 = Math.cos(latitude2);
        double[] var10 = new double[3];
        double[] var20 = new double[3];
        var10[0] = var4 * var3;
        var10[1] = var4 * var1;
        var10[2] = var2;
        var20[0] = var8 * var7;
        var20[1] = var8 * var5;
        var20[2] = var6;
 
        return Math.asin(Math.sqrt((var10[0] - var20[0]) * (var10[0] - var20[0]) + (var10[1] - var20[1]) * (var10[1] - var20[1]) + (var10[2] - var20[2]) * (var10[2] - var20[2])) / 2.0) * 1.27420015798544E7;
        // 结果四舍五入 保留2位小数
        //return new BigDecimal(distance).setScale(2, RoundingMode.HALF_UP).doubleValue();
    }
 
}

5.方法五

该方法是利用第三方jar包计算

5.1 POM引入第三方依赖


    <!--用于计算两点之间的距离-->
    <dependency>
        <groupId>org.gavaghan</groupId>
        <artifactId>geodesy</artifactId>
        <version>1.1.3</version>
    </dependency>

5.2 代码


package com.test.java.util;
 
import org.gavaghan.geodesy.Ellipsoid;
import org.gavaghan.geodesy.GeodeticCalculator;
import org.gavaghan.geodesy.GeodeticCurve;
import org.gavaghan.geodesy.GlobalCoordinates;
 
/**
 * 坐标位置相关util
 */
public class PositionUtil {
 
    /**
     * 方法四：（利用第三方jar包计算）
     * 计算两个经纬度之间的距离
     *
     * @param longitude1 第一点的经度
     * @param latitude1  第一点的纬度
     * @param longitude2 第二点的经度
     * @param latitude2  第二点的纬度
     * @param ellipsoid  计算方式
     * @return 返回的距离，单位m
     */
    public static double getDistance4(double longitude1, double latitude1, double longitude2, double latitude2, Ellipsoid ellipsoid) {
        // 创建GeodeticCalculator，调用计算方法，传入坐标系、经纬度用于计算距离
        GlobalCoordinates firstPoint = new GlobalCoordinates(latitude1, longitude1);
        GlobalCoordinates secondPoint = new GlobalCoordinates(latitude2, longitude2);
        GeodeticCurve geoCurve = new GeodeticCalculator().calculateGeodeticCurve(ellipsoid, firstPoint, secondPoint);
        return geoCurve.getEllipsoidalDistance();
    }
 
}

6.测试结果对比

这里我直接一起调用者4种方法，这样看结果也更加直观些。


    public static void main(String[] args) {
 
        double longitude1 = 117.344733;
        double latitude1 = 31.912334;
        double longitude2 = 117.272186;
        double latitude2 = 31.79422;
 
        double distance1 = PositionUtil.getDistance1(longitude1, latitude1, longitude2, latitude2);
        double distance2 = PositionUtil.getDistance2(longitude1, latitude1, longitude2, latitude2);
        double distance3 = PositionUtil.getDistance3(longitude1, latitude1, longitude2, latitude2);
        double distance4 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2);
        double distance5 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2, Ellipsoid.Sphere);
        double distance6 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2, Ellipsoid.WGS84);
 
 
        System.out.println("方法1算出的距离：" + distance1);
        System.out.println("方法2算出的距离：" + distance2);
        System.out.println("方法3算出的距离：" + distance3);
        System.out.println("方法4算出的距离：" + distance4);
        System.out.println("方法4-Sphere算出的距离：" + distance5);
        System.out.println("方法4-WGS84算出的距离：" + distance6);
    }

可以看出，这几个方法算出的距离误差相对较小。而且main方法中提供的测试数据也是我自身的真实数据，结合百度地图的测距工具进行的测试。有需要的小伙伴，可以自行选择合适的方法。

二、校验经纬度是否在制定区域内

怎么样判断一个坐标点在指定的区域内？其中区域又会分为：圆，多边形和不规则的多边形。

1.判断一个坐标是否在圆形区域内

计算这个坐标点和圆心之间的距离，然后跟圆的半径进行比较，如果比半径大，就不在圆形区域内，如果小于等于圆的半径，则该坐标点在圆形区域内。


package com.test.java.util;
 
import org.apache.commons.lang3.StringUtils;
 
/**
 * 计算距离
 */
public class PositionUtil {
 
    /**
     * 赤道半径（单位：米）
     */
    private static final double EQUATOR_RADIUS = 6378137;
 
    /**
     * 方法一：（反余弦计算方式）
     *
     * @param longitude1 第一个点的经度
     * @param latitude1  第一个点的纬度
     * @param longitude2 第二个点的经度
     * @param latitude2  第二个点的纬度
     * @return 返回距离，单位m
     */
    public static double getDistance1(double longitude1, double latitude1, double longitude2, double latitude2) {
        // 纬度
        double lat1 = Math.toRadians(latitude1);
        double lat2 = Math.toRadians(latitude2);
        // 经度
        double lon1 = Math.toRadians(longitude1);
        double lon2 = Math.toRadians(longitude2);
        // 纬度之差
        double a = lat1 - lat2;
        // 经度之差
        double b = lon1 - lon2;
        // 计算两点距离的公式
        double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(lat1) * Math.cos(lat2) * Math.pow(Math.sin(b / 2), 2)));
        // 弧长乘赤道半径, 返回单位: 米
        s = s * EQUATOR_RADIUS;
        return s;
    }
 
    /**
     * 判断坐标点是否在圆形区域内
     * 计算这个坐标点和圆心点之间的距离，然后跟圆的半径进行比较，如果比半径大，就不在圆形区域内，如果小于等于圆的半径，则该坐标点在圆形区域内
     *
     * @param longitude1 第一点的经度
     * @param latitude1  第一点的纬度
     * @param longitude2 第二点的经度
     * @param latitude2  第二点的纬度
     * @param radius     圆形范围半径（单位：米）
     * @return true：不在区域内; false:在区域内
     */
    public static boolean isInCircle(double longitude1, double latitude1, double longitude2, double latitude2, String radius) {
        if (StringUtils.isBlank(radius)) {
            throw new RuntimeException("请输入范围半径");
        }
        return getDistance1(longitude1, latitude1, longitude2, latitude2) > Double.parseDouble(radius);
    }
 
}

2.判断一个坐标是否在一个多边形区域内

这里用到JAVA的一个类GeneralPath（由直线和二次和三次（B？zier）曲线构成的几何路径。它可以包含多个子路径）使用这个类，结合传入的各顶点参数，画一个几何图形，并通过它自身的contains方法，判断该点是否在这个几何图形内。


package com.test.java.util;
 
import org.apache.commons.lang3.StringUtils;
 
import java.awt.geom.GeneralPath;
import java.awt.geom.Point2D;
import java.util.ArrayList;
import java.util.List;
 
/**
 * 计算距离
 */
public class PositionUtil {
 
    /**
     * 判断坐标点是否在多边形区域内
     *
     * @param pointLon 要判断的点的经度
     * @param pointLat 要判断的点的纬度
     * @param lon      区域各顶点的经度数组
     * @param lat      区域各顶点的纬度数组
     * @return true：范围内; false：范围外
     */
    public static boolean isInPolygon(double pointLon, double pointLat, double[] lon, double[] lat) {
        // 将要判断的横纵坐标组成一个点
        Point2D.Double point = new Point2D.Double(pointLon, pointLat);
        // 将区域各顶点的横纵坐标放到一个点集合里面
        List<Point2D.Double> pointList = new ArrayList<>();
        double polygonPointToX;
        double polygonPointToY;
        for (int i = 0; i < lon.length; i++) {
            polygonPointToX = lon[i];
            polygonPointToY = lat[i];
            Point2D.Double polygonPoint = new Point2D.Double(polygonPointToX, polygonPointToY);
            pointList.add(polygonPoint);
        }
        return check(point, pointList);
    }
 
    /**
     * 坐标点是否在多边形内
     *
     * @param point   要判断的点的横纵坐标
     * @param polygon 组成的顶点坐标集合
     */
    private static boolean check(Point2D.Double point, List<Point2D.Double> polygon) {
        GeneralPath generalPath = new GeneralPath();
 
        Point2D.Double first = polygon.get(0);
        // 通过移动到指定坐标（以双精度指定），将一个点添加到路径中
        generalPath.moveTo(first.x, first.y);
        polygon.remove(0);
        for (Point2D.Double d : polygon) {
            // 通过绘制一条从当前坐标到新指定坐标（以双精度指定）的直线，将一个点添加到路径中。
            generalPath.lineTo(d.x, d.y);
        }
        // 将几何多边形封闭
        generalPath.lineTo(first.x, first.y);
        generalPath.closePath();
        // 测试指定的 Point2D 是否在 Shape 的边界内。
        return generalPath.contains(point);
    }
 
}

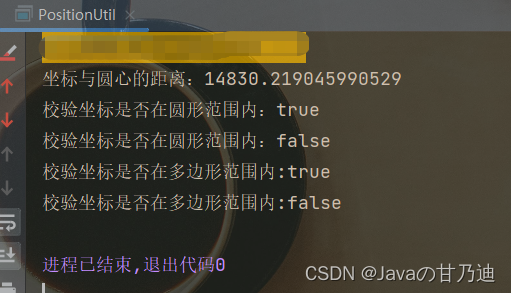
3.结果


    public static void main(String[] args) {
 
        double distance1 = PositionUtil.getDistance1(longitude1, latitude1, longitude2, latitude2);
        System.out.println("坐标与圆心的距离：" + distance1);
 
        String radius1 = "10000";
        boolean inCircle1 = PositionUtil.isInCircle(longitude1, latitude1, longitude2, latitude2, radius1);
        System.out.println("校验坐标是否在圆形范围内：" + inCircle1);
 
        String radius = "15000";
        boolean inCircle2 = PositionUtil.isInCircle(longitude1, latitude1, longitude2, latitude2, radius);
        System.out.println("校验坐标是否在圆形范围内：" + inCircle2);
 
        double pointLon = 117.274984;
        double pointLat = 31.790718;
 
        // 坐标在多边形范围内的参数：
        double[] lon = {117.272559, 117.276224, 117.278649, 117.273924};
        double[] lat = {31.791247, 31.792812, 31.78982, 31.788539};
 
        // 坐标在多边形范围外的参数：
        double[] lon1 = {117.291001, 117.299705, 117.298035, 117.291216};
        double[] lat1 = {31.806576, 31.806814, 31.802319, 31.802196};
 
        boolean a = PositionUtil.isInPolygon(pointLon, pointLat, lon, lat);
        boolean b = PositionUtil.isInPolygon(pointLon, pointLat, lon1, lat1);
        System.out.println("校验坐标是否在多边形范围内:" + a);
        System.out.println("校验坐标是否在多边形范围内:" + b);
    }

总结

这样的计算方式得到的距离并非是真实的距离，可以说是逻辑距离（直线距离），但其距离也已经很准确。不过毕竟是通过逻辑计算得到的距离，若要求高准确性的距离信息的话，还是借助第三方的地图api接口获取比较合适。

如果这篇文章对您有所帮助，或者有所启发的话，求一键三连：点赞、评论、收藏➕关注，您的支持是我坚持写作最大的动力。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/空白诗007/article/detail/736613