【AI隐私保护.论文笔记】CrypTFlow2: Practical 2-Party Secure Inference，CrypTFlow2：实用的安全两方推理

这篇文章提出了实用的安全两方推理，能够实现安全神经网络的推理，发表在2020年安全类顶会CSS，由微软研究院的印度研究组完成。他们基于以前的密码学工作，衡量了安全和效率等多方面的问题，提出了一个叫做CrypTFlow2安全两方计算的机器学习框架。
以前的激活层，Relu，Sigmoid函数大部分是采用GC，或者近似函数的方式。GC的开销比较大，而近似函数都有精度损失。比如CryptoNets中使用的是x的平方作为激活层，CHET中使用$a{x}^2+bx$作为激活函数。本论文基于新的比较函数提出了新的激活层Relu的计算方法。
主要的贡献有三个方面
一，对于百万富翁问题，提出了一个新比较协议。然后把该协议应用到了DRelu上，能够计算神经网络的非线性层，例如ReLU, Maxpool 和 Argmax.
二，提出了新的除法算法。利用这种算法进行乘法的无误差截断处理，使用OT和HE计算线性层乘法，然后截断处理。以前的乘法截断都是直接截断，已经被证明会产生巨大的误差。
三，提出了一个新的框架CrypTFlow2，这个框架线性层，分别使用两种不同的密码技术实现，一个是基于同态的SCI,一个是基于OT的SCI。

一：贡献

新的百万富翁问题

首先介绍百万富翁问题，两个富翁想要在不透露自己持有资产的数量下比较谁更有钱，抽象到数学表示，就是：参与方有$P_0$,$P_1$,他们分别持有整数$x$,$y$，想要不透露这两个数的基础上得到比较$x<y$的结果。这两个数用二进制表示，都是$l$位的，即可以用$l$位的比特串来表示。
作者提出的协议理论上比当前最好的比较协议，通信量复杂度（communication complexity ）降低了3倍，通信轮次复杂性（ round complexity）是$lo{g}_{2}l$。
下图表一详细介绍了一些常用安全比较的密码学方法的通信量复杂度和轮次复杂度，例如GC混淆电路，GMW，SC3和该协议。其中$m$是本协议引入的参数，$\lambda$是加密算法引入的参数。作者分别计算了$m=4，7$和$\lambda =128$情况下的通信量和轮次。

使用这种比较协议，就可以计算DRelu函数，然后计算神经网络的非线性层，如Relu和MaxPool。

实现乘法和卷积运算则使用到了基于同态或OT的除法。这种设置使得框架在不同的网络配置比较灵活。
对于Relu这些非线性的运算过去大部分采用的是GC混淆电路的方法，基于本论文提出的协议实现的Relu函数比以前纯GC的方法减少了8倍到12倍的通信量。具体的比较见下图的表2.

定点数的计算

过去的模型都是基于定点数的计算。给定的安全推理任务中，进行除法运算时，舍弃了一部分的正确性，往往求的是除法的近似。定点的乘法中，两数相乘，因为小数位数不变，相乘的结果每次都要除以2的幂次，在计算机中就是移位计算，这就导致了精度的损失。同时，在神经网络的线性计算的过程中，需要的最多次数的计算就是乘法。这就导致了误差不断增加。最近的一篇论文已经显示，这种不断增加的误差最后会导致分类精度的显著损失。
作者提供了新的协议来计算对于2的幂的除法和任意整数除法，并且证明了这种协议的正确性和有效性。
对于计算$l$位的除法，当前能够正确计算的就是GC混淆电路。下图中比较了在Avgpool层分别使用GC和作者使用的协议的效率。

扩展到DNN

以前的很多工作都是基于MNIST和CIFAR数据集,在MNIST数据集中，识别的都是黑白图像。本论文把工作应用到了Imagenet领域，Imagenet的数据更复杂，一般都是彩色的，需要在上个类别中分类。
本作也是第一个把安全加密扩展到ResNet50和DenseNet121网络上的。相比于以前的工作，效果更好，更实用。

OT vs HE

选择OT还是同态加密，尽管最初的安全推理工作使用基于OT的协议来计算卷积，但目前提供最佳推理延迟的最先进的协议使用基于HE来计算卷积。
基于HE的安全推理通信比OT少得多，但需要更多的计算量。因此，在这项工作开始时，作者并不清楚基于HE的卷积是否能为映像级别的基准测试提供最佳延迟。
为了解决这个问题，作者分别实现了基于这两种协议的工作。
线性层使用OT或同态，也用到了作者提到的除法，非线性使用作者提出的比较协议。
WAN网络环境下，HE工作的更快。LAN的设置下，两种方法没有区别。

二： 使用的技巧

百万富翁问题

对于百万富翁问题，作者使用的方法基于以前提出的一种比较的方法。
对于要比较的$x$,$y$，定义$x=x_1||x_0,y=y_1||y_0$，其中$||$表示字符串的拼接。判断是否$x<y$就可以分段判别，第一种，判断是否$x_1<y_1$，或者第二种判断$x_1=y_1$并且$x_0=y_0$.原始位的比较问题现在缩小到更短比特的子问题上，其实这里使用了分治的思想。不断地分割串，就可以得到一个比较树，每个叶子节点都是一位的比较，每一位的比较可以通过1-out-of-2 OT协议实现。然而，这样操作下来通信量也是很大的，因此，考虑一种基于m参数的分割。即分割$logl/m$次，最后每个叶子节点的大小是m位。之后就可以使用1-out-of-2^m OT协议，基于2017年提出的一种查表的LUTs方案比较m位数的大小。从叶子节点到根节点的递归需要基于Beaver bit triple的AND函数。
注意到在2次AND实例中使用了相同的秘密值。因此,构建相关双三元组使用1-out-of-8 OT协议，降低成本。1-out-of-8 OT协议的实现使用了2013年的一个OT扩展协议，该OT扩展实现传输短秘密值的条件下提高OT扩展协议的效率

DRelu函数

令$a$,是$a_0,a_1$在合适的环上的秘密分享，想要计算DRelu（$a$)。考虑两种情况，一种是$l$位上的即$Z_L$环上的秘密分享，一种是$Z_n$整数上的秘密分享。
基于位数的秘密分享：

基于整数的秘密分享：
分别计算DRelu的值。

除法和截断

作者把基于$Z_L$，$Z_n$环上的除法分解转换为基于校正项的秘密分享。这些修正项由秘密值上的多个不等式组成。修正项的不等式可以用之前提出的百万富翁的新协议来计算，而秘密分享的除法可以由各参与方在当地完成。这种技术是DNN推理任务的安全实现的关键，因为它，才能够获得与明文定点数实现DNN任务按位等价的效果。

其他相关工作

Raphael Bost是第一个提出基于密码学的神经网络推理，SecureML是第一个提出基于密码学的推理和训练。一些能够支持恶意敌手的框架如SPDZ,一些支持二值权重的框架如XONN,等。

三 ：基础知识

威胁模型与安全

本文基于抵抗半诚实概率多项式时间的敌手A的仿真范例，提供安全证明。这也是一种被称为UC安全的方法。半诚实模型是说有一个计算边界的敌手在协议开始的时候已经攻陷两个参与方中的一个，但是它遵守协议规范继续执行协议。
安全定义在两种交互的场景下，实际场景中，$P_0$,$P_1$,在存在敌手A的环境Z中执行协议，理想环境中，参与方把他们的输入发给一个执行理想函数不会泄露任何信息的第三方。实现安全性要求对于现实中敌手A，理想场景中，存在一个仿真器S，从而使环境Z无法区分在真实还是在理想中执行交互计算。

密码学原语：准备工作

秘密分享：简单的 2-out-of-2 的加法秘密分享。
OT茫然传输：采用了一种茫然传输扩展，2013年提出的一种优化框架，实现短秘密的 -out-of-n 茫然传输。发送方有n个的数据，接受方根据自己的输入，从中得到一个对应数据。发送方不知道接收方得到的哪个数据，接收方除了自己应该得到的数据，其他数据都不知道，因此实现了安全性。还使用了COT的一种茫然传输方案，也是2013年提出的。
OT扩展一般是一种减少OT执行开销的方法。一次OT需要执行一次公钥密码操作，但是公钥加密的开销通常远大于对称加密的开销。OT扩展只需要k次公钥操作结合任意次数对称加密，可以实现任意次数的OT.IKNP协议是第一个高效率的OT扩展协议。更具体的参考OT扩展的实现

COT：这种茫然传输方案也是13年提出的。翻译过来就是相关OT,本来OT中发送方发送的两个数据是没有关系的，在COT中发送方的两个数据可以满足某种函数关系。
发送方的输出是这个函数的输入，接受方的输出是这个函数的输出。

普通OT要发送两个数据，COT只需要发送一个相关数据。在COT中，发送方提供一种相关性，信息是在这个约束下随机生成的。
COT扩展实例需要提供批次大小l.
每个批次，接收方提供$l$长度的0或1的串，表示进行l次数据的选择。发送方提供一个$l$长度的相关向量。
函数选择$l$个随机pads，发送给发送方。如果选择方的选择位是0，发送pads,如果选择位是1，发送pads和相关量的和。

实现：

最初的目的是提高GC混淆电路中OT的执行效率。下面的论文是从原论文找到的具体描述。其中还涉及到XOR和point-and-permute。

数据选择器和B2A转换：
$F_m^n$表示数据选择器，使用两次OT实现。
a是一个$P_0$,$P_1$分享的秘密，表示为$<a{>}_0^n$,$<a{>}_1^n$，n表示是在n大小的环上的秘密分享。c是$P_0$,$P_1$分享的一个二进制的比特位的秘密，表示为$<c{>}_0^n$,$<c{>}_1^n$,c只能取值为0或者1，它的秘密分享值也只能取0或者1。该函数的目的是秘密分享的计算a*c。附录中给出了具体的实现：

$F_{B2A}^n$把比特位的分享转换为数字上的分享，把环从2变成了n。但是数不变。
调用了一次COT。这个协议最开始提出来是为了简化gc混淆电路中的OT协议。

与门的使用
比较算法中还用了一个与门的协议，不是普通的与门，是在二进制秘密分享上的与门。使用到bit-triples的方法。下面图具体描述了协议，
看完了这个协议感觉察觉到了使用OT协议的方法本质，就是发送方把计算结果枚举出来，然后接收方利用自己的输入选择对应的结果，发送方消息的序号对应了接收方的输入的可能选项。在这个过程中，不透露其他的消息还有接收方的输入。

还有一个优化的与门的方案，叫做相关与门协议，用于节省传输开销。进行与操作时，正如协议中描述的那样，相同的时候可以采用这种方式。

四：百万富翁协议具体实现

作者想法来自于之前一个比较算法的研究，他们看到：

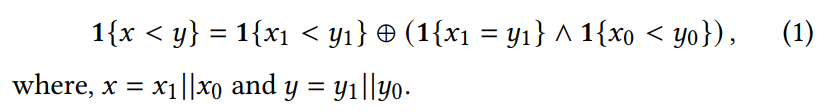
即比较两个数的算法，可以拆分成子串上的比较，有点分治法的意思。
介绍一些基本的符号，l是需要比较的数的二进制位数，一般取32,16等。m是一个参数，令q=l/m，为了方便计算，选择m,使q为2的幂次，例如让q=4或者8等。M=2^m。把长度为l的串分成q部分，每个部分的长度为m.有：

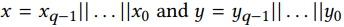
然后在构建的树中从下到上依次计算，得到协议的结果。

详细的协议如下，下面介绍协议的具体内容：
输入：$P_0$输入x,$P_1$输入y,这两个数都是l位的二进制串
输出：$P_0$,$P_1$分别得到比较结果的秘密分享值，一个比特位。
第一步：$P_0$把输入x分成q个子串，$P_1$把输入y分成q个子串，每个子串的大小是m。
第二步：设M=2^m
第三步：对于j=0到q-1进行循环。
第四步：$P_0$随机选择两个比特位。这两个比特位是用于得到结果的秘密分享的。
第五步：对于k=0到M-1循环.
第六步：$P_0$设置发送的$s_{j,k}$,s用于得到不等式$x_j<k$的值
第七步：$P_0$设置发送的$t_{j,k}$，t用于得到等式$x_j=k$的值
第八步：结束k的循环
第九步：$P_0$,$P_1$调用1-out-of-M OT协议，即从M个数据$s_{j,k}$中选择一个。$P_0$作为发送方，,输入是M个数据$s_{j,k}$，$P_1$作为接收方，输入是$y_j$。
第十步：$P_0$,$P_1$调用1-out-of-M OT协议，即从M个数据$s_{j,k}$中选择一个。$P_0$作为发送方，,输入是M个数据$t_{j,k}$，$P_1$作为接收方，输入是$y_j$。
第十一步：结束j的循环
第十二步：对于i等于1到$logq$
第十三步：对于j等于0到$q/2^i-1$
第十四步：计算等式和不等式的与
第十五步：本地进行异或操作就可以了。因为异或相当于相加，根据秘密分享的可加性，可以本地计算。
第十六步：计算等式和等式的与，用于上一层等式的判断。注意此时比特位的含义代表的是比较的结果，而非x，y本身的位。
第十七步：结束j的循环
第十八步：结束i的循环
第十九步：输出最后的结果。

正确性分析：
作者就是简单地推导了得到的输出结果能够等于比较的结果。安全性遵循了OT和$F_{AND}$混合协议的安全性。

考虑一般的情况：
第一种：m不能够整除l的情况下，对于l mod m=r，也就是l除以m的余数，单独拿出来运行。
第二种：q不是2的幂次时，考虑$2^a<q<=2^{a+1}$,取$2^a$部分作为构建完美二叉树的片段。最后把完美二叉树求出的比较的值和剩余部分再进行一次比较即可。

算法优化：
一：第九步和第十步中，都用到了OT，可以把两个1位的1-out-of-M整合成一个2位的1-out-of-M。因为$P_1$的输入都是$y_j$
二：十四和十六步中，都用到了AND，利用相关AND，即有相同输入的AND协议，节省开销。
三：对于整棵二叉树而言，最低有效位的分叉的等式从未被使用到，所以可以不用计算。

l位数的整数的DRelu协议

l位整数的DRelu协议相对简单，因为它采用的大小为$Z_L$的环，$L=2^l$。即可以采用补码的方式表示，最高有效位是1的时候表示负数，最高有效位是0的时候表示正数。

环n上的整数的DRelu协议

协议的优化

五：除法和截断处理

作者给出了在环上用正整数除法和截断(除以2的幂)的安全实现的结果，它们按位等效于相应的明文计算。首先使用每种协议的封闭形式表达式，然后是使用他们的协议。
使用idiv表示有符号的整数除法，其中商舍入到负无穷，商的符号取决于被除数和除数的符号。余数r的符号与除数的符号相同。

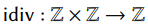
使用rdiv表示一个环元素除以一个正整数。

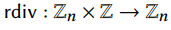
rdiv具体的定义如下，其中$a_u$表示a在环n上的正整数，属于（0,n)。为了简单，使用$x{=}_{n}y$表示
$x$ mod n $=$ $y$ mod n。

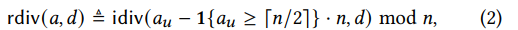
定理4.1：$<a{>}_0^n$,$<a{>}_1^n$是$a$在环n上的秘密分享。令$n=n^1\ast d+n^0$,其中$n^1,n^0,d$属于整数Z，并且$0<=n^0<d<n$。
详细的实现过程如下，证明的过程在附录C.

理论4.2：用于截断的除法，是整数除法的一种特殊情况。

理论4.2的证明：

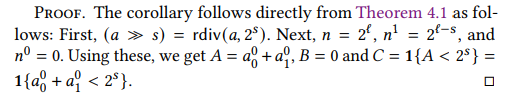
具体的除法协议

下面讨论两种不同设置情况下的除法，第一种是l位的除法，第二种是模为n除法。
第一种：数字是l位的秘密分享的情况下，为了实现s位截断，使用以下协议：
输入：

环n上的除法的协议，这个协议大部分和l位的协议相同，不同的地方在于三次符号的比较。其中C公式可以表示为：

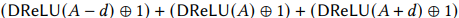
三次调用DRelu协议即可。此外，计算C还需要知道A的值，需要得到A公式的秘密分享的值。计算A公式的值还需要corr公式的秘密分享的值。由于篇幅限制作者把具体的协议贴在了附录。正确性证明和复杂度分析也在附录C。

六：安全推理

神经网络一般分成线性层和非线性层。
设置$P_0$为模型的拥有者。为了模块化的实现安全推理，设置每层的输入和输出都是秘密分享的。这使得我们可以顺序地为任意层缝合协议，从而为由这些层组成的任何神经网络获得一个安全的计算协议。协议的半诚实安全性将简单地由各个子协议的顺序组合而来。$SC{I}_{O}T$的秘密分享方案基于$Z_L$的环，$SC{I}_{H}E$的秘密分享方案基于$Z_n$的环。

线性层

包括全连接层和卷积层，使用定点数进行计算，当用定点数计算后，再使用作者提出的除法协议进行截断。
基于OT协议的乘法：作者简单地描述了基于OT协议的乘法，以下是99年一篇论文中详细描述。
使用COT和结构化矩阵乘法进行了优化。

基于HE协议的乘法：作者使用了和Gazella和Delphi相同的同态线性乘法。在高级别上,首先,$P_1$发送加密的秘密分享给$P_0$,$P_0$计算输出结果，返回给$P_1$加密的秘密分享的结果，以便进行下一次的计算。

avgpool的计算，先把各自的秘密分享相加，然后调用一次除法即可。

非线性层

Relu层：Relu=DRelu*a.所以使用DRelu协议还有数据选择器就能计算出Rule的值了。

Maxpool层：计算最大池化层的协议。
采用的是两两比较选出最大的方法。先选出两个里面的大的数，再依次往后比较。
对于x,y两个在$P_0$,$P_1$秘密分享的数，先本地计算各自的秘密分享的x-y=w。将两个秘密分享的w输入DRelu协议，看w是否大于0，结果设置为v。再利用一个数据选择器，t=wv.最后各自输出的z=y+t。
考虑v=0时，t=0,输出的z=y。
考虑v=1时，t=w=x-y输出的z=y+x-y=x。

七：实现

作者在一个库中实现了该论文中的加密协议，并将它们集成到之前的工作CrypTFlow框架中作为一个新的加密后端。CrypTFlow使用其前端Athos编译高级TensorFlow推断代码，以保护计算协议，然后由其加密后端执行。为了支持可靠的定点算法，我们修正了Athos的截断行为。首先描述密码库的实现，然后是对Athos所做的修改。
OT协议使用的是16年王萧的emp库。
同态加密使用的Delphi的框架，使用过的SEAL的库。
CrypTFlow需要64位宽来确保其协议中本地截断错误的概率很小。由于我们的协议是正确的，并且没有这样的错误，我们扩展了Athos，通过自动调整验证集来优化位宽和规模。
权重的位宽和规模会泄漏信息和这个泄漏在前面关于安全推理的工作都存在。
我们在Athos中实现以下窥视孔优化以减少这些截断调用的成本。不在卷积后立即截断运行完relu之后再截断、
这种优化进一步考虑了可能发生在卷积和ReLU之间的操作，比如矩阵加法。将截断的调用后立即卷积后ReLU意味着激活流入加法操作现在2