最小生成树详解(模板 + 例题)

作为一个伪ACMer,先来首广为人知的打油诗:
模拟只会猜题意，贪心只能过样例，数学上来先打表，规律一般是DP，组合数学碰运气，计算几何瞎暴力，图论一顿套模板，数论只会GCD,递归递推伤不起，搜索茫然TLE，分治做得像枚举，暴力枚举数第一，数据结构干瞪眼，怒刷水题找信心。

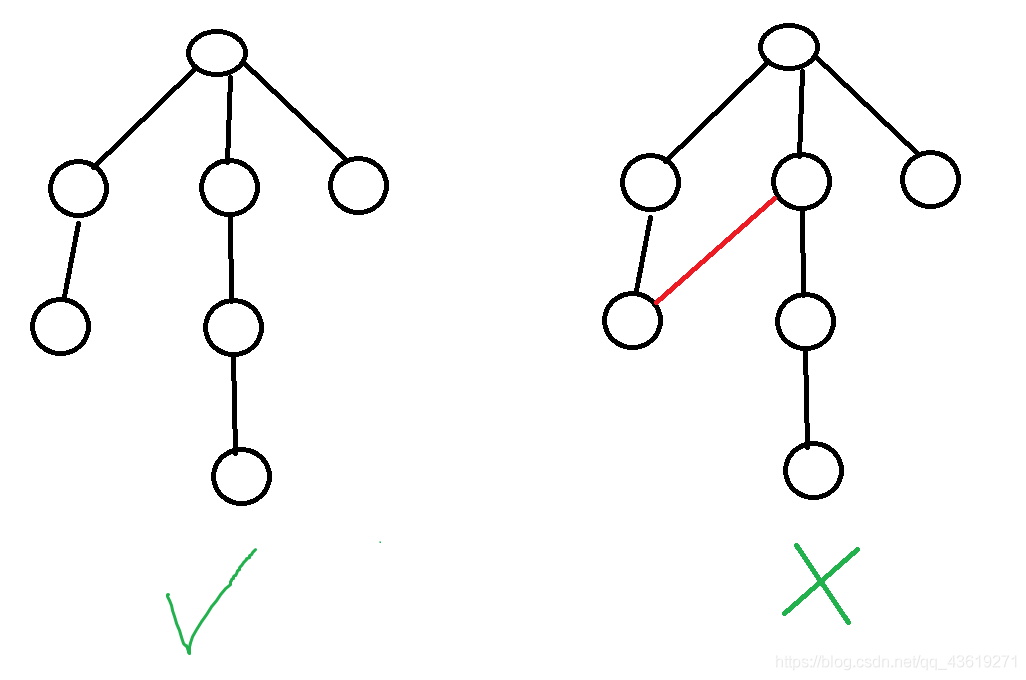
1、什么是树

如果一个无向连通图不包含回路(连通图中不存在环),那么就是一个树。

2、最小生成树

一个图中可能存在多条相连的边,我们一定可以从一个图中挑出一些边生成一棵树。这仅仅是生成一棵树,还未满足最小,当图中每条边都存在权重时,这时候我们从图中生成一棵树(n - 1 条边)时,生成这棵树的总代价就是每条边的权重相加之和。

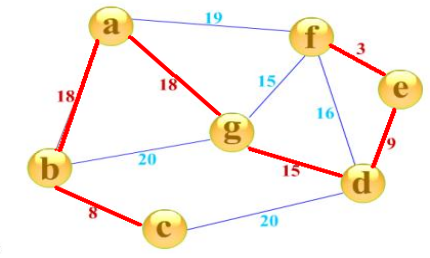
一个有N个点的图，边一定是大于等于N-1条的。图的最小生成树，就是在这些边中选择N-1条出来，连接所有的N个点。这N-1条边的边权之和是所有方案中最小的。

3、最小生成树的应用

要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

4、实现最小生成树的两种算法

4.1 prim (普里姆算法)

算法分析:

Prim算法每次循环都将一个蓝点u变为白点，并且此蓝点u与白点相连的最小边权min[u]还是当前所有蓝点中最小的。这样相当于向生成树中添加了n-1次最小的边，最后得到的一定是最小生成树。

我们通过对下图最小生成树的求解模拟来理解上面的思想。蓝点和虚线代表未进入最小生成树的点、边；白点和实线代表已进入最小生成树的点、边。

初始时所有点都是蓝点，min[1]=0,min[2、3、4、5]=∞。权值之和MST=0。

第一次循环自然是找到min[1]=0最小的蓝点1。将1变为白点，接着枚举与1相连的所有蓝点2、3、4，修改它们与白点相连的最小边权。

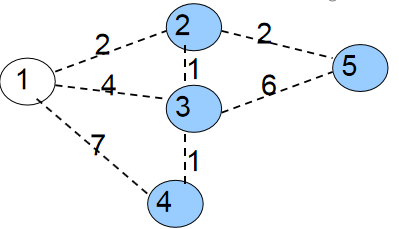
min[2]=w[1][2]=2;
min[3]=w[1][3]=4;
min[4]=w[1][4]=7；
第二次循环是找到min[2]最小的蓝点2。将2变为白点，接着枚举与2相连的所有蓝点3、5，修改它们与白点相连的最小边权。

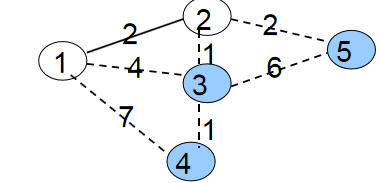
min[3]=w[2][3]=1;
min[5]=w[2][5]=2;

第三次循环是找到min[3]最小的蓝点3。将3变为白点，接着枚举与3相连的所有蓝点4、5，修改它们与白点相连的最小边权。

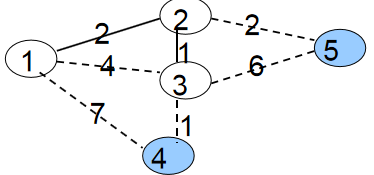
min[4]=w[3][4]=1;
由于min[5]=2 < w[3][5]=6;所以不修改min[5]的值。
最后两轮循环将点4、5以及边w[2][5],w[3][4]添加进最小生成树。

最后权值之和MST=6。这n次循环，每次循环我们都能让一个新的点加入生成树，n次循环就能把所有点囊括到其中；每次循环我们都能让一条新的边加入生成树，n-1次循环就能生成一棵含有n个点的树；每次循环我们都取一条最小的边加入生成树，n-1次循环结束后，我们得到的就是一棵最小的生成树。这就是Prim采取贪心法生成一棵最小生成树的原理。算法时间复杂度：O (N2)。

精彩例题:

题目链接:https://www.acwing.com/problem/content/860/

Code:

	// prim 算法求最小生成树 
	
	#include <cstdio>
	#include <string>
	#include <cstring>
	#include <iostream>
	#include <algorithm>
	
	#define INF 0x3f3f3f3f
	
	using namespace std;
	
	const int maxn = 505;
	
	int a[maxn][maxn];
	
	int vis[maxn],dist[maxn];
	
	int n,m;
	
	int u,v,w;
	
	long long sum = 0;
	
	int prim(int pos) {
		dist[pos] = 0;
		// 一共有 n 个点,就需要 遍历 n 次,每次寻找一个权值最小的点,记录其下标
		for(int i = 1; i <= n; i ++) {
			int cur = -1;
			for(int j = 1; j <= n; j ++) {
				if(!vis[j] && (cur == -1 || dist[j] < dist[cur])) {
					cur = j;
				}
			}
			// 这里需要提前终止
			if(dist[cur] >= INF) return INF;
			sum += dist[cur];
			vis[cur] = 1;
			for(int k = 1; k <= n; k ++) {
			    // 只更新还没有找到的最小权值
				if(!vis[k]) dist[k] = min(dist[k],a[cur][k]);
			}
		}
		return sum;
	}
	
	int main(void) {
		scanf("%d%d",&n,&m);
		memset(a,0x3f,sizeof(a));
		memset(dist,0x3f,sizeof(dist));
		for(int i = 1; i <= m; i ++) {
			scanf("%d%d%d",&u,&v,&w);
			a[u][v] = min(a[u][v],w);
			a[v][u] = min(a[v][u],w);
		}
		int value = prim(1);
		if(value >= INF) puts("impossible");
		else printf("%lld\n",sum);
		return 0;
	} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

4.2 kruskal (克鲁斯卡尔算法)

Kruskal（克鲁斯卡尔）算法是一种巧妙利用并查集来求最小生成树的算法。

算法描述:

在描述 kruskal 算法时先了解一下连通块的概念, 我们将无向图中相互连通的一些点称为处于同一个连通块中。

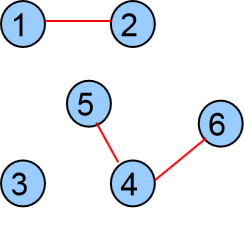
从上图我们可以清晰的看到,有 3 个连通块(1,2),(3),(4,5,6)。

Kruskal算法将一个连通块当做一个集合。Kruskal首先将所有的边按从小到大顺序排序（一般使用快排），并认为每一个点都是孤立的，分属于n个独立的集合。然后按顺序枚举每一条边。如果这条边连接着两个不同的集合，那么就把这条边加入最小生成树，这两个不同的集合就合并成了一个集合；如果这条边连接的两个点属于同一集合，就跳过。直到选取了n-1条边为止。

Kruskal（克鲁斯卡尔）算法开始时，认为每一个点都是孤立的，分属于n个独立的集合。

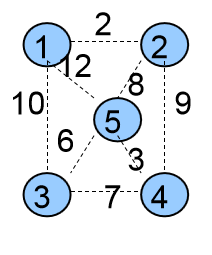
5个集合{ {1}，{2}，{3}，{4}，{5} }

生成树中没有边
Kruskal每次都选择一条最小的边，而且这条边的两个顶点分属于两个不同的集合。将选取的这条边加入最小生成树，并且合并集合。
第一次选择的是<1,2>这条边，将这条边加入到生成树中，并且将它的两个顶点1、2合并成一个集合。

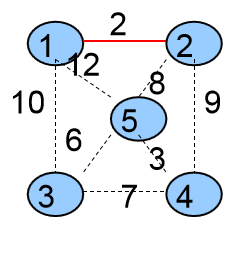
4个集合{ {1，2}，{3}，{4}，{5} }
生成树中有一条边{ <1,2> }
第二次选择的是<4,5>这条边，将这条边加入到生成树中，并且将它的两个顶点4、5合并成一个集合。

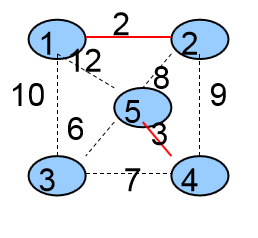
3个集合{ {1，2}，{3}，{4，5} }
生成树中有2条边{ <1,2> ，<4,5>}
第三次选择的是<3,5>这条边，将这条边加入到生成树中，并且将它的两个顶点3、5所在的两个集合合并成一个集合

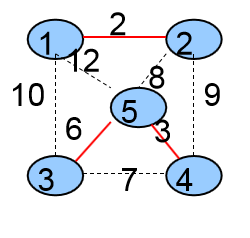
2个集合{ {1，2}，{3，4，5} }
生成树中有3条边{ <1,2> ，<4,5>，< 3，5>}
第四次选择的是<2,5>这条边，将这条边加入到生成树中，并且将它的两个顶点2、5所在的两个集合合并成一个集合。

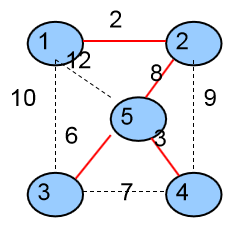
1个集合{ {1，2，3，4，5} }
生成树中有4条边{ <1,2> ，<4,5>，< 3，5>，<2,5>}
算法结束，最小生成树权值为19。

通过上面的模拟能够看到，Kruskal算法每次都选择一条最小的，且能合并两个不同集合的边，一张n个点的图总共选取n-1次边。因为每次我们选的都是最小的边，所以最后的生成树一定是最小生成树。每次我们选的边都能够合并两个集合，最后n个点一定会合并成一个集合。通过这样的贪心策略，Kruskal算法就能得到一棵有n-1条边，连接着n个点的最小生成树。

精彩例题:

题目链接:https://www.acwing.com/problem/content/861/

Code:

	// Kruskal 算法求最小生成树 
	
	#include <cstdio>
	#include <string>
	#include <cstring>
	#include <iostream>
	#include <algorithm>
	
	using namespace std;
	
	const int maxn = 2e5 + 10; 
	
	struct node {
		int x,y,z;
	}edge[maxn];
	
	bool cmp(node a,node b) {
		return a.z < b.z;
	}
	
	int fa[maxn];
	
	int n,m;
	
	int u,v,w; 
	
	long long sum;
	
	int get(int x) {
		return x == fa[x] ? x : fa[x] = get(fa[x]);
	}
	
	int main(void) {
		scanf("%d%d",&n,&m);
		for(int i = 1; i <= m; i ++) {
			scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z);
		}
		for(int i = 0; i <= n; i ++) {
			fa[i] = i;
		}
		sort(edge + 1,edge + 1 + m,cmp);
		// 每次加入一条最短的边
		for(int i = 1; i <= m; i ++) {
			int x = get(edge[i].x);
			int y = get(edge[i].y);
			if(x == y) continue;
			fa[y] = x;
			sum += edge[i].z;
		}
		int ans = 0;
		for(int i = 1; i <= n; i ++) {
			if(i == fa[i]) ans ++;
		}
		if(ans > 1) puts("impossible");
		else printf("%lld\n",sum);
		return 0;
	} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

5、总结

从上面的两道模板可得知,解决最小生成树的问题一般有两种方式:prim 和 Kruskal ,那么,什么时候选择哪种策略就成为了我们应该思考的一个问题:
稀疏图一般选择 prim,采用 邻接矩阵 进行存储边之间的关系。
稠密图一般选择 Kruskal ,采用邻接表进行存储边之间的关系(更多采用结构体的方式)。

参考链接:https://www.cnblogs.com/SeanOcean/p/10975694.html