【 Vue 】Diff 算法上

渲染器的核心Diff算法

减小DOM操作的性能开销

上一章我们讨论了渲染器是如何更新各种类型的 VNode 的，实际上，上一章所讲解的内容归属于完整的 Diff 算法之内，但并不包含核心的 Diff 算法。那什么才是核心的 Diff 算法呢？看下图：

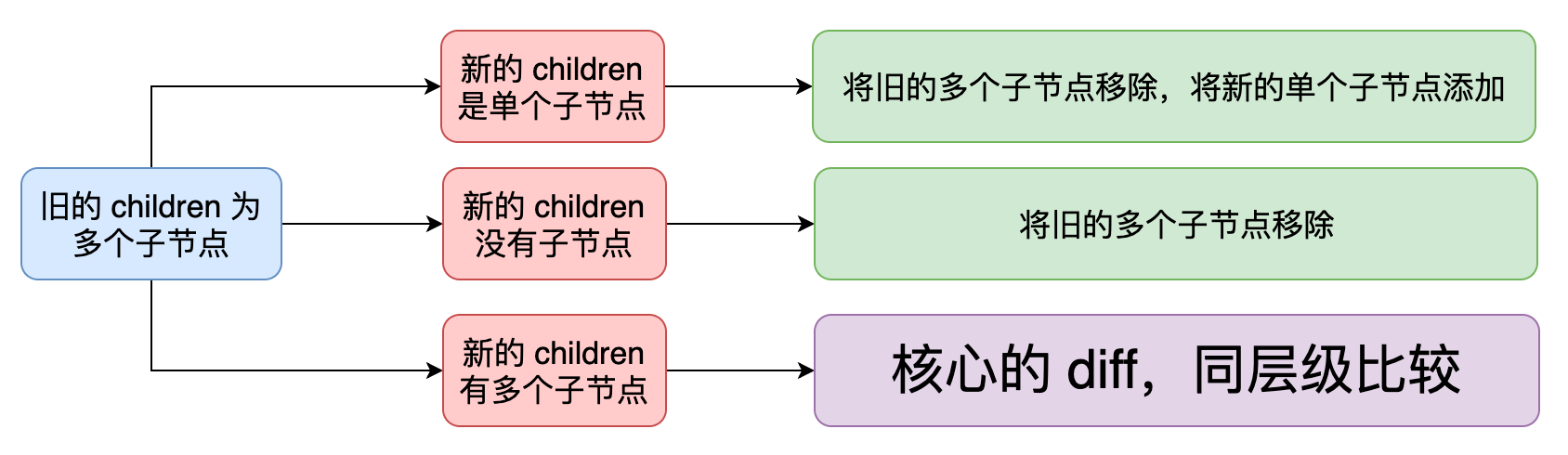
我们曾在上一章中讲解子节点更新的时候见到过这张图，当时我们提到只有当新旧子节点的类型都是多个子节点时，核心 Diff 算法才派得上用场，并且当时我们采用了一种仅能实现目标但并不完美的算法：遍历旧的子节点，将其全部移除；再遍历新的子节点，将其全部添加，如下高亮代码所示：

function patchChildren(
  prevChildFlags,
  nextChildFlags,
  prevChildren,
  nextChildren,
  container
) {
  switch (prevChildFlags) {
    // 省略...

    // 旧的 children 中有多个子节点
    default:
      switch (nextChildFlags) {
        case ChildrenFlags.SINGLE_VNODE:
          // 省略...
        case ChildrenFlags.NO_CHILDREN:
          // 省略...
        default:
          // 新的 children 中有多个子节点
          // 遍历旧的子节点，将其全部移除
          for (let i = 0; i < prevChildren.length; i++) {
            container.removeChild(prevChildren[i].el)
          }
          // 遍历新的子节点，将其全部添加
          for (let i = 0; i < nextChildren.length; i++) {
            mount(nextChildren[i], container)
          }
          break
      }
      break
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

为了便于表述，我们把这个算法称为：简单 Diff 算法。简单 Diff 算法虽然能够达到目的，但并非最佳处理方式。我们经常会遇到可排序的列表，假设我们有一个由 li 标签组成的列表：

<ul>
  <li>1</li>
  <li>2</li>
  <li>3</li>
</ul>

1
2
3
4
5
6

列表中的 li 标签是 ul 标签的子节点，我们可以使用下面的数组来表示 ul 标签的 children：

[
  h('li', null, 1),
  h('li', null, 2),
  h('li', null, 3)
]

1
2
3
4
5
6

接着由于数据变化导致了列表的顺序发生了变化，新的列表顺序如下：

[
  h('li', null, 3),
  h('li', null, 1),
  h('li', null, 2)
]

1
2
3
4
5
6

新的列表和旧的列表构成了新旧 children，当我们使用简单 Diff 算法更新这两个列表时，其操作行为可以用下图表示：

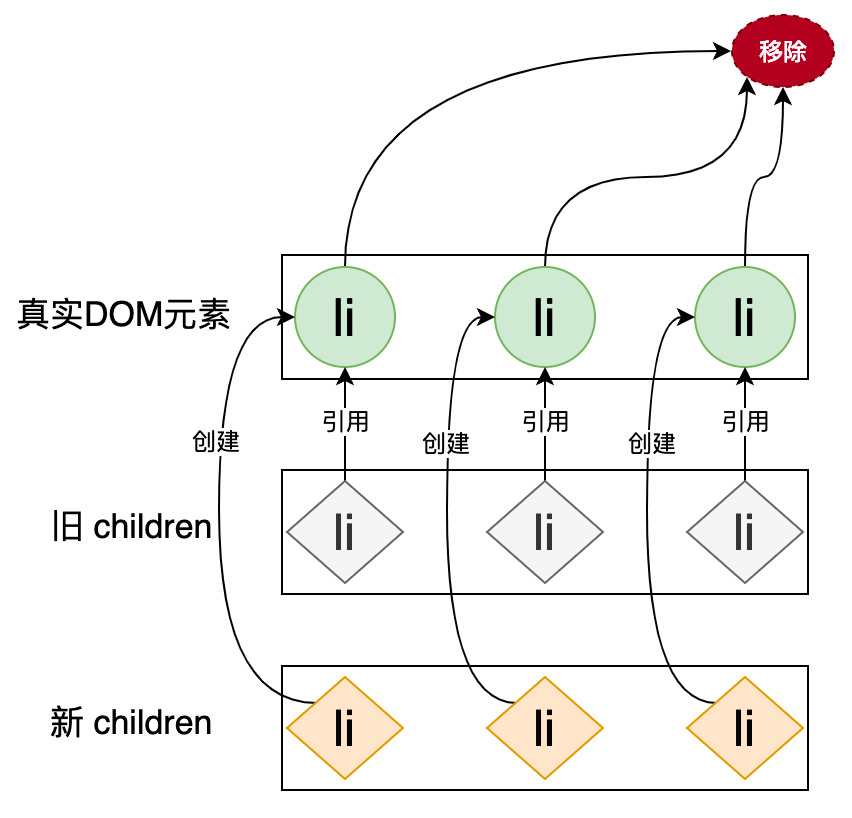
在这张图中我们使用圆形表示真实 DOM 元素，用菱形表示 VNode，旧的 VNode 保存着对真实 DOM 的引用(即 vnode.el 属性)，新的 VNode 是不存在对真实 DOM 的引用的。上图描述了简单 Diff 算法的操作行为，首先遍历旧的 VNode，通过旧 VNode 对真实 DOM 的引用取得真实 DOM，即可将已渲染的 DOM 移除。接着遍历新的 VNode 并将其全部添加到页面中。

在这个过程中我们能够注意到：更新前后的真实 DOM 元素都是 li 标签。那么可不可以复用 li 标签呢？这样就能减少“移除”和“新建” DOM 元素带来的性能开销，实际上是可以的，我们在讲解 patchElement 函数时了解到，当新旧 VNode 所描述的是相同标签时，那么这两个 VNode 之间的差异就仅存在于 VNodeData 和 children 上，所以我们完全可以通过遍历新旧 VNode，并一一比对它们，这样对于任何一个 DOM 元素来说，由于它们都是相同的标签，所以更新的过程是不会“移除”和“新建”任何 DOM 元素的，而是复用已有 DOM 元素，需要更新的只有 VNodeData 和 children。优化后的更新操作可以用下图表示：

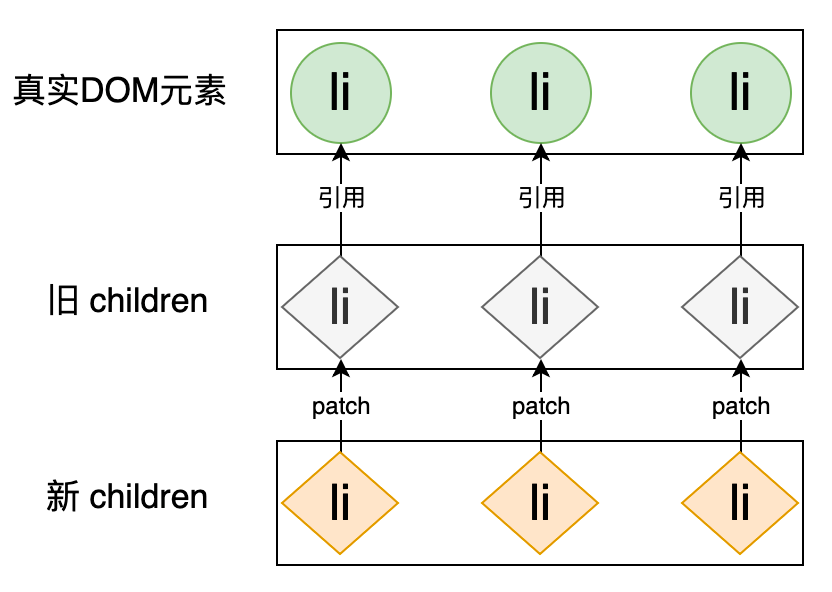
用代码实现起来也非常简单，如下高亮代码所示：

function patchChildren(
  prevChildFlags,
  nextChildFlags,
  prevChildren,
  nextChildren,
  container
) {
  switch (prevChildFlags) {
    // 省略...

    // 旧的 children 中有多个子节点
    default:
      switch (nextChildFlags) {
        case ChildrenFlags.SINGLE_VNODE:
          // 省略...
        case ChildrenFlags.NO_CHILDREN:
          // 省略...
        default:
          for (let i = 0; i < prevChildren.length; i++) {
            patch(prevChildren[i], nextChildren[i], container)
          }
          break
      }
      break
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

通过遍历旧的 children，将新旧 children 中相同位置的节点拿出来作为一对“新旧 VNode”，并调用 patch 函数更新之。由于新旧列表的标签相同，所以这种更新方案较之前相比，省去了“移除”和“新建” DOM 元素的性能开销。而且从实现上看，代码也较之前少了一些，真可谓一举两得。但不要高兴的太早，细心的同学可能已经发现问题所在了，如上代码中我们遍历的是旧的 children，如果新旧 children 的长度相同的话，则这段代码可以正常工作，但是一旦新旧 children 的长度不同，这段代码就不能正常工作了，如下图所示：

当新的 children 比旧的 children 的长度要长时，多出来的子节点是没办法应用 patch 函数的，此时我们应该把多出来的子节点作为新的节点添加上去。类似的，如果新的 children 比旧的 children 的长度要短时，我们应该把旧的 children 中多出来的子节点移除，如下图所示：

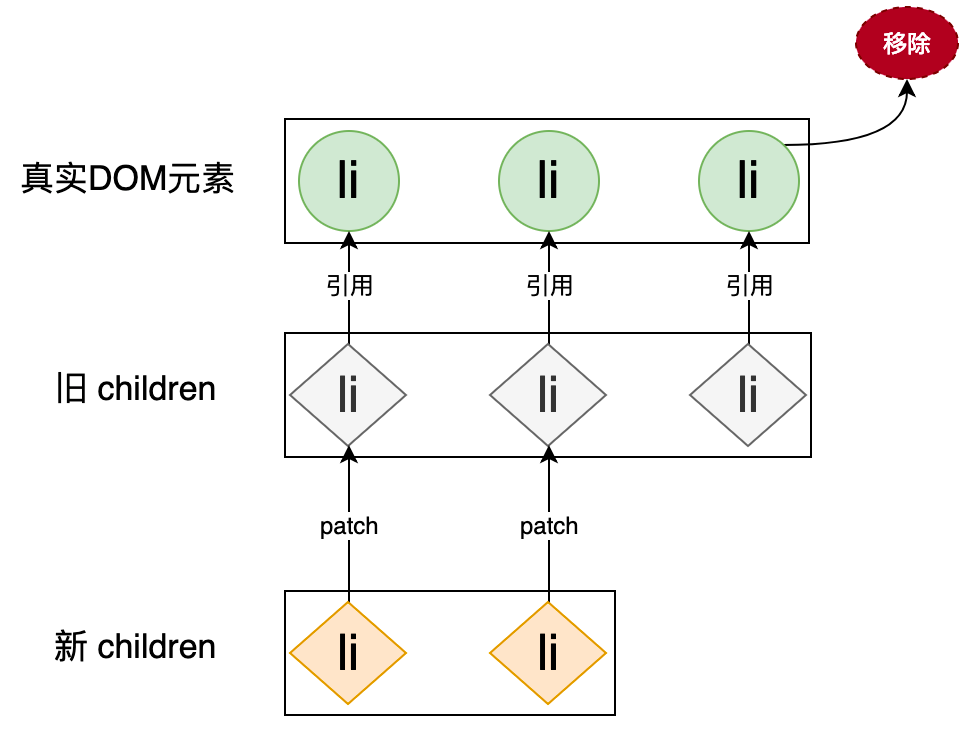
通过分析我们得出一个规律，我们不应该总是遍历旧的 children，而是应该遍历新旧 children 中长度较短的那一个，这样我们能够做到尽可能多的应用 patch 函数进行更新，然后再对比新旧 children 的长度，如果新的 children 更长，则说明有新的节点需要添加，否则说明有旧的节点需要移除。最终我们得到如下实现：

function patchChildren(
  prevChildFlags,
  nextChildFlags,
  prevChildren,
  nextChildren,
  container
) {
  switch (prevChildFlags) {
    // 省略...

    // 旧的 children 中有多个子节点
    default:
      switch (nextChildFlags) {
        case ChildrenFlags.SINGLE_VNODE:
          // 省略...
        case ChildrenFlags.NO_CHILDREN:
          // 省略...
        default:
          // 新的 children 中有多个子节点
          // 获取公共长度，取新旧 children 长度较小的那一个
          const prevLen = prevChildren.length
          const nextLen = nextChildren.length
          const commonLength = prevLen > nextLen ? nextLen : prevLen
          for (let i = 0; i < commonLength; i++) {
            patch(prevChildren[i], nextChildren[i], container)
          }
          // 如果 nextLen > prevLen，将多出来的元素添加
          if (nextLen > prevLen) {
            for (let i = commonLength; i < nextLen; i++) {
              mount(nextChildren[i], container)
            }
          } else if (prevLen > nextLen) {
            // 如果 prevLen > nextLen，将多出来的元素移除
            for (let i = commonLength; i < prevLen; i++) {
              container.removeChild(prevChildren[i].el)
            }
          }
          break
      }
      break
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

实际上，这个算法就是在没有 key 时所采用的算法，该算法是存在优化空间的，下面我们将分析如何进一步优化。

尽可能的复用 DOM 元素

key 的作用

在上一小节中，我们通过减少 DOM 操作的次数使得更新的性能得到了提升，但它仍然存在可优化的空间，要明白如何优化，那首先我们需要知道问题出在哪里。还是拿上一节的例子来说，假设旧的 children 如下：

[
  h('li', null, 1),
  h('li', null, 2),
  h('li', null, 3)
]

1
2
3
4
5
6

新的 children 如下：

[
  h('li', null, 3),
  h('li', null, 1),
  h('li', null, 2)
]

1
2
3
4
5
6

我们来看一下，如果使用前面讲解的 Diff 算法来更新这对新旧 children 的话，会进行哪些操作：首先，旧 children 的第一个节点和新 children 的第一个节点进行比对(patch)，即：

h('li', null, 1)
// vs
h('li', null, 3)

1
2
3
4

patch 函数知道它们是相同的标签，所以只会更新 VNodeData 和子节点，由于这两个标签都没有 VNodeData，所以只需要更新它们的子节点，旧的 li 元素的子节点是文本节点 ‘1’，而新的 li 标签的子节点是文本节点 ‘3’，所以最终会调用一次 patchText 函数将 li 标签的文本子节点由 ‘1’ 更新为 ‘3’。接着，使用旧 children 的第二个节点和新 children 的第二个节点进行比对，结果同样是调用一次 patchText 函数用以更新 li 标签的文本子节点。类似的，对于新旧 children 的第三个节点同样也会调用一次 patchText 函数更新其文本子节点。而这，就是问题所在，实际上我们通过观察新旧 children 可以很容易的发现：新旧 children 中的节点只有顺序是不同的，所以最佳的操作应该是通过移动元素的位置来达到更新的目的。

既然移动元素是最佳期望，那么我们就需要思考一下，能否通过移动元素来完成更新？能够移动元素的关键在于：我们需要在新旧 children 的节点中保存映射关系，以便我们能够在旧 children 的节点中找到可复用的节点。这时候我们就需要给 children 中的节点添加唯一标识，也就是我们常说的 key，在没有 key 的情况下，我们是没办法知道新 children 中的节点是否可以在旧 children 中找到可复用的节点的，如下图所示：

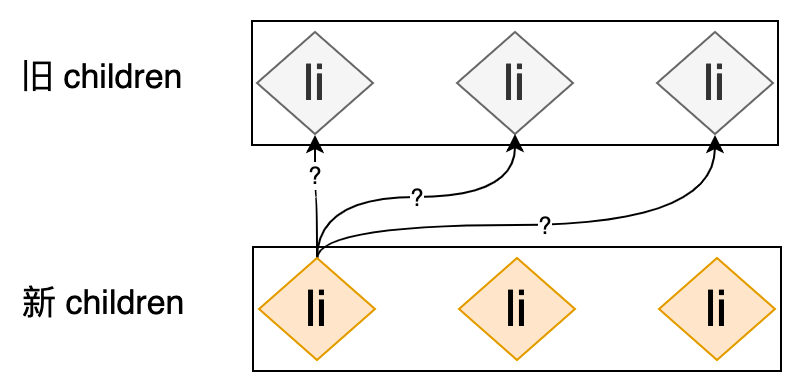
新旧 children 中的节点都是 li 标签，以新 children 的第一个 li 标签为例，你能说出在旧 children 中哪一个 li 标签可被它复用吗？不能，所以，为了明确的知道新旧 children 中节点的映射关系，我们需要在 VNode 创建伊始就为其添加唯一的标识，即 key 属性。

我们可以在使用 h 函数创建 VNode 时，通过 VNodeData 为即将创建的 VNode 设置一个 key：

h('li', { key: 'a' }, 1)

1
2

但是为了 diff 算法更加方便的读取一个 VNode 的 key，我们应该在创建 VNode 时将 VNodeData 中的 key 添加到 VNode 本身，所以我们需要修改一下 h 函数，如下：

export function h(tag, data = null, children = null) {
  // 省略...

  // 返回 VNode 对象
  return {
    _isVNode: true,
    flags,
    tag,
    data,
    key: data && data.key ? data.key : null,
    children,
    childFlags,
    el: null
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

如上代码所示，我们在创建 VNode 时，如果 VNodeData 中存在 key 属性，则我们会把其添加到 VNode 对象本身。

现在，在创建 VNode 时已经可以为 VNode 添加唯一标识了，我们使用 key 来修改之前的例子，如下：

// 旧 children
[
  h('li', { key: 'a' }, 1),
  h('li', { key: 'b' }, 2),
  h('li', { key: 'c' }, 3)
]

// 新 children
[
  h('li', { key: 'c' }, 3)
  h('li', { key: 'a' }, 1),
  h('li', { key: 'b' }, 2)
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14

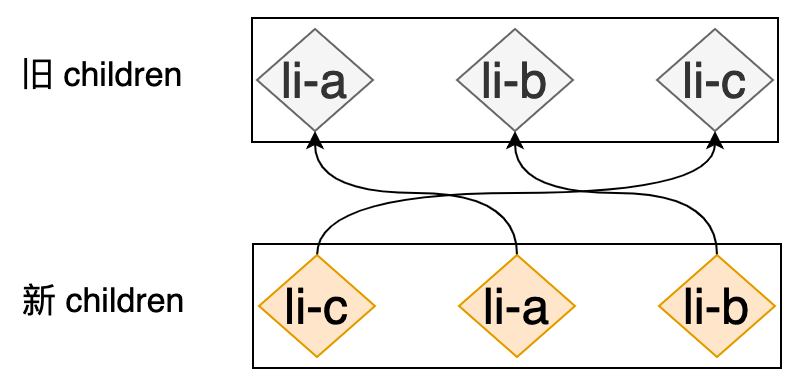
有了 key 我们就能够明确的知道新旧 children 中节点的映射关系，如下图所示：

// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0
  // 遍历旧的 children
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之
    if (nextVNode.key === prevVNode.key) {
      patch(prevVNode, nextVNode, container)
      break // 这里需要 break
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

这段代码中有两层嵌套的 for 循环语句，外层循环用于遍历新 children，内层循环用于遍历旧 children，其目的是尝试寻找具有相同 key 值的两个节点，如果找到了，则认为新 children 中的节点可以复用旧 children 中已存在的节点，这时我们仍然需要调用 patch 函数对节点进行更新，如果新节点相对于旧节点的 VNodeData 和子节点都没有变化，则 patch 函数什么都不会做(这是优化的关键所在)，如果新节点相对于旧节点的 VNodeData 或子节点有变化，则 patch 函数保证了更新的正确性。

找到需要移动的节点

现在我们已经找到了可复用的节点，并进行了合适的更新操作，下一步需要做的，就是判断一个节点是否需要移动以及如何移动。如何判断节点是否需要移动呢？为了弄明白这个问题，我们可以先考虑不需要移动的情况，当新旧 children 中的节点顺序不变时，就不需要额外的移动操作，如下：

我们同样执行一下本节介绍的算法，看看会发生什么：

1、取出新 children 的第一个节点，即 li-c，并尝试在旧 children 中寻找 li-c，结果是我们找到了，并且 li-c 在旧 children 中的索引为 2。
2、取出新 children 的第二个节点，即 li-a，并尝试在旧 children 中寻找 li-a，也找到了，并且 li-a 在旧 children 中的索引为 0。
到了这里，递增的趋势被打破了，我们在寻找的过程中先遇到的索引值是 2，接着又遇到了比 2 小的 0，这说明在旧 children 中 li-a 的位置要比 li-c 靠前，但在新的 children 中 li-a 的位置要比 li-c 靠后。这时我们就知道了 li-a 是那个需要被移动的节点，我们接着往下执行。

3、取出新 children 的第三个节点，即 li-b，并尝试在旧 children 中寻找 li-b，同样找到了，并且 li-b 在旧 children 中的索引为 1。
我们发现 1 同样小于 2，这说明在旧 children 中节点 li-b 的位置也要比 li-c 的位置靠前，但在新的 children 中 li-b 的位置要比 li-c 靠后。所以 li-b 也需要被移动。

以上我们过程就是我们寻找需要移动的节点的过程，在这个过程中我们发现一个重要的数字：2，是这个数字的存在才使得我们能够知道哪些节点需要移动，我们可以给这个数字一个名字，叫做：寻找过程中在旧 children 中所遇到的最大索引值。如果在后续寻找的过程中发现存在索引值比最大索引值小的节点，意味着该节点需要被移动。

实际上，这就是 React 所使用的算法。我们可以使用一个叫做 lastIndex 的变量存储寻找过程中遇到的最大索引值，并且它的初始值为 0，如下代码所示：

// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0
  // 遍历旧的 children
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之
    if (nextVNode.key === prevVNode.key) {
      patch(prevVNode, nextVNode, container)
      if (j < lastIndex) {
        // 需要移动
      } else {
        // 更新 lastIndex
        lastIndex = j
      }
      break // 这里需要 break
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

如上代码中，变量 j 是节点在旧 children 中的索引，如果它小于 lastIndex 则代表当前遍历到的节点需要移动，否则我们就使用 j 的值更新 lastIndex 变量的值，这就保证了 lastIndex 所存储的总是我们在旧 children 中所遇到的最大索引。

移动节点

现在我们已经有办法找到需要移动的节点了，接下来要解决的问题就是：应该如何移动这些节点？为了弄明白这个问题，我们还是先来看下图：

新 children 中的第一个节点是 li-c，它在旧 children 中的索引为 2，由于 li-c 是新 children 中的第一个节点，所以它始终都是不需要移动的，只需要调用 patch 函数更新即可，如下图：

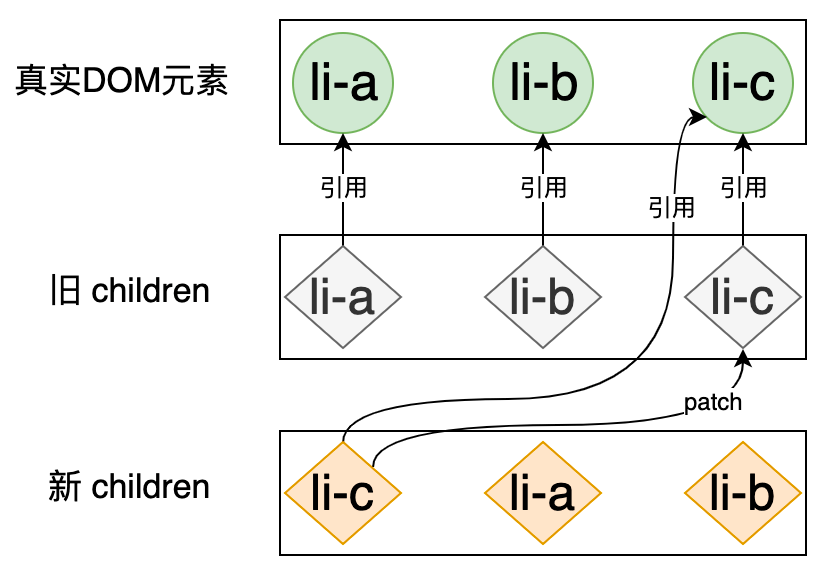
这里我们需要注意的，也是非常重要的一点是：新 children 中的 li-c 节点在经过 patch 函数之后，也将存在对真实 DOM 元素的引用。下面的代码可以证明这一点：

function patchElement(prevVNode, nextVNode, container) {
  // 省略...

  // 拿到 el 元素，注意这时要让 nextVNode.el 也引用该元素
  const el = (nextVNode.el = prevVNode.el)

  // 省略...
}

beforeCreate() {
  this.$options.data = {...}
}

1
2
3
4
5
6
7
8
9
10
11
12
13

如上代码所示，这是 patchElement 函数中的一段代码，在更新新旧 VNode 时，新的 VNode 通过旧 VNode 的 el 属性实现了对真实 DOM 的引用。为什么说这一点很关键呢？继续往下看。

li-c 节点更新完毕，接下来是新 children 中的第二个节点 li-a，它在旧 children 中的索引是 0，由于 0 < 2 所以 li-a 是需要移动的节点，那应该怎么移动呢？很简单，新 children 中的节点顺序实际上就是更新完成之后，节点应有的最终顺序，通过观察新 children 可知，新 children 中 li-a 节点的前一个节点是 li-c，所以我们的移动方案应该是：把 li-a 节点对应的真实 DOM 移动到 li-c 节点所对应真实 DOM 的后面。这里的关键在于移动的是真实 DOM 而非 VNode。所以我们需要分别拿到 li-c 和 li-a 所对应的真实 DOM，这时就体现出了上面提到的关键点：新 children 中的 li-c 已经存在对真实 DOM 的引用了，所以我们很容易就能拿到 li-c 对应的真实 DOM。对于获取 li-a 节点所对应的真实 DOM 将更加容易，由于我们当前遍历到的节点就是 li-a，所以我们可以直接通过旧 children 中的 li-a 节点拿到其真实 DOM 的引用，如下代码所示：

// 用来存储寻找过程中遇到的最大索引值
let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0
  // 遍历旧的 children
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 `patch` 函数更新之
    if (nextVNode.key === prevVNode.key) {
      patch(prevVNode, nextVNode, container)
      if (j < lastIndex) {
        // 需要移动
        // refNode 是为了下面调用 insertBefore 函数准备的
        const refNode = nextChildren[i - 1].el.nextSibling
        // 调用 insertBefore 函数移动 DOM
        container.insertBefore(prevVNode.el, refNode)
      } else {
        // 更新 lastIndex
        lastIndex = j
      }
      break // 这里需要 break
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

观察如上代码段中高亮的部分，实际上这两句代码即可完成 DOM 的移动操作。我们来对这两句代码的工作方式做一个详细的解释，假设我们当前正在更新的节点是 li-a，那么如上代码中的变量 i 就是节点 li-a 在新 children 中的位置索引。所以 nextChildren[i - 1] 就是 li-a 节点的前一个节点，也就是 li-c 节点，由于 li-c 节点存在对真实 DOM 的引用，所以我们可以通过其 el 属性拿到真实 DOM，到了这一步，li-c 节点的所对应的真实 DOM 我们已经得到了。但不要忘记我们的目标是：把 li-a 节点对应的真实 DOM 移动到 li-c 节点所对应真实 DOM 的后面，所以我们的思路应该是想办法拿到 li-c 节点对应真实 DOM 的下一个兄弟节点，并把 li-a 节点所对应真实 DOM 插到该节点的前面，这才能保证移动的正确性。所以上面的代码中常量 refNode 引用是 li-c 节点对应真实 DOM 的下一个兄弟节点。拿到了正确的 refNode 之后，我们就可以调用容器元素的 insertBefore 方法来完成 DOM 的移动了，移动的对象就是 li-a 节点所对应的真实 DOM，由于当前正在处理的就是 li-a 节点，所以 prevVNode 就是旧 children 中的 li-a 节点，它是存在对真实 DOM 的引用的，即 prevVNode.el。万事俱备，移动工作将顺利完成。说起来有些抽象，用一张图可以更加清晰的描述这个过程：

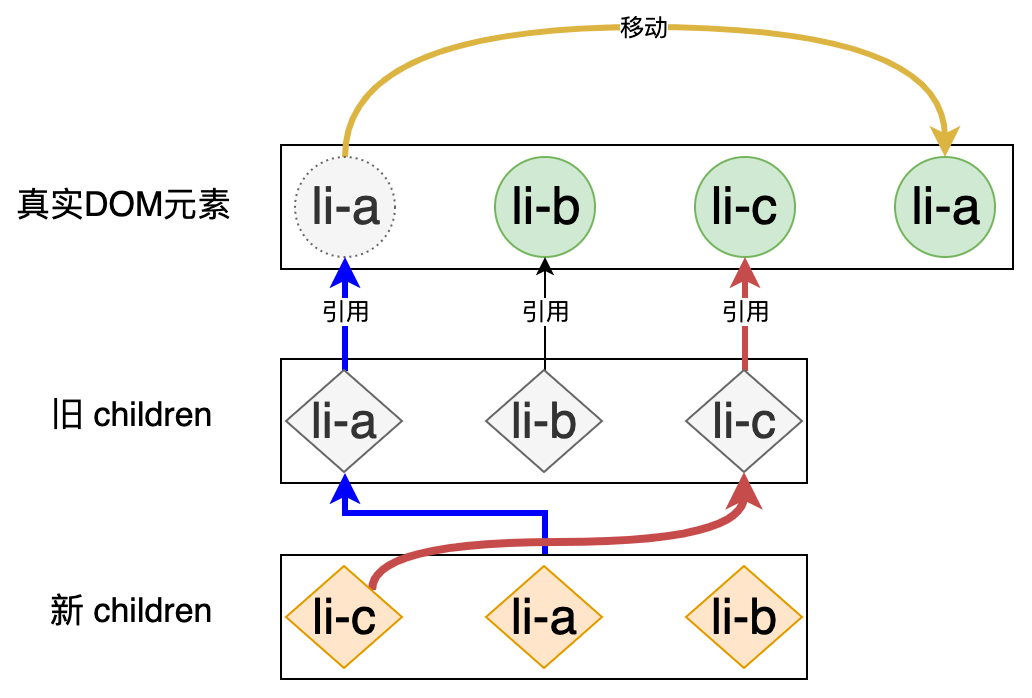
观察不同颜色的线条，关键在于我们要找到 VNode 所引用的真实 DOM，然后把真实 DOM 按照新 children 中节点间的关系进行移动，由于新 children 中节点的顺序就是最终的目标顺序，所以移动之后的真实 DOM 的顺序也会是最终的目标顺序。

添加新元素

在上面的讲解中，我们一直忽略了一个问题，即新 children 中可能包含那些不能够通过移动来完成更新的节点，例如新 children 中包含了一个全新的节点，这意味着在旧 children 中是找不到该节点的，如下图所示：

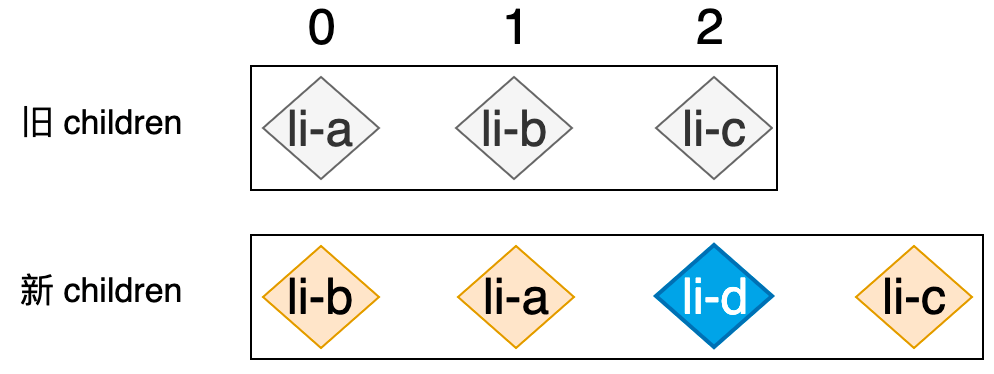
节点 li-d 在旧的 children 中是不存在的，所以当我们尝试在旧的 children 中寻找 li-d 节点时，是找不到可复用节点的，这时就没办法通过移动节点来完成更新操作，所以我们应该使用 mount 函数将 li-d 节点作为全新的 VNode 挂载到合适的位置。

我们将面临两个问题，第一个问题是：如何知道一个节点在旧的 children 中是不存在的？这个问题比较好解决，如下代码所示：

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0,
    find = false
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    if (nextVNode.key === prevVNode.key) {
      find = true
      patch(prevVNode, nextVNode, container)
      if (j < lastIndex) {
        // 需要移动
        const refNode = nextChildren[i - 1].el.nextSibling
        container.insertBefore(prevVNode.el, refNode)
        break
      } else {
        // 更新 lastIndex
        lastIndex = j
      }
    }
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

如上高亮代码所示，我们在原来的基础上添加了变量 find，它将作为一个标志，代表新 children 中的节点是否存在于旧 children 中，初始值为 false，一旦在旧 children 中寻找到了相应的节点，我们就将变量 find 的值设置为 true，所以如果内层循环结束后，变量 find 的值仍然为 false，则说明在旧的 children 中找不到可复用的节点，这时我们就需要使用 mount 函数将当前遍历到的节点挂载到容器元素，如下高亮的代码所示：

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0,
    find = false
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    if (nextVNode.key === prevVNode.key) {
      find = true
      patch(prevVNode, nextVNode, container)
      if (j < lastIndex) {
        // 需要移动
        const refNode = nextChildren[i - 1].el.nextSibling
        container.insertBefore(prevVNode.el, refNode)
        break
      } else {
        // 更新 lastIndex
        lastIndex = j
      }
    }
  }
  if (!find) {
    // 挂载新节点
    mount(nextVNode, container, false)
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

当内层循环结束之后，如果变量 find 的值仍然为 false，则说明 nextVNode 是全新的节点，所以我们直接调用 mount 函数将其挂载到容器元素 container 中。但是很遗憾，这段代码不能正常的工作，这是因为我们之前编写的 mountElement 函数存在缺陷，它总是调用 appendChild 方法插入 DOM 元素，所以上面的代码始终会把新的节点作为容器元素的最后一个子节点添加到末尾，这不是我们想要的结果，我们应该按照节点在新的 children 中的位置将其添加到正确的地方，如下图所示：

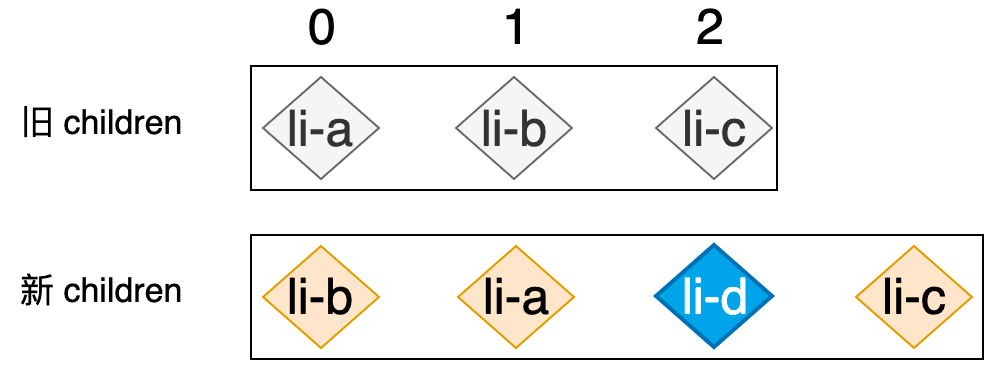
新的 li-d 节点紧跟在 li-a 节点的后面，所以正确的做法应该是把 li-d 节点添加到 li-a 节点所对应真实 DOM 的后面才行。如何才能保证 li-d 节点始终被添加到 li-a 节点的后面呢？答案是使用 insertBefore 方法代替 appendChild 方法，我们可以找到 li-a 节点所对应真实 DOM 的下一个节点，然后将 li-d 节点插入到该节点之前即可，如下高亮代码所示：

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0,
    find = false
  for (j; j < prevChildren.length; j++) {
    const prevVNode = prevChildren[j]
    if (nextVNode.key === prevVNode.key) {
      find = true
      patch(prevVNode, nextVNode, container)
      if (j < lastIndex) {
        // 需要移动
        const refNode = nextChildren[i - 1].el.nextSibling
        container.insertBefore(prevVNode.el, refNode)
        break
      } else {
        // 更新 lastIndex
        lastIndex = j
      }
    }
  }
  if (!find) {
    // 挂载新节点
    // 找到 refNode
    const refNode =
      i - 1 < 0
        ? prevChildren[0].el
        : nextChildren[i - 1].el.nextSibling
    mount(nextVNode, container, false, refNode)
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

我们先找到当前遍历到的节点的前一个节点，即 nextChildren[i - 1]，接着找到该节点所对应真实 DOM 的下一个子节点作为 refNode，即 nextChildren[i - 1].el.nextSibling，但是由于当前遍历到的节点有可能是新 children 的第一个节点，这时 i - 1 < 0，这将导致 nextChildren[i - 1] 不存在，所以当 i - 1 < 0 时，我们就知道新的节点是作为第一个节点而存在的，这时我们只需要把新的节点插入到最前面即可，所以我们使用 prevChildren[0].el 作为 refNode。最后调用 mount 函数挂载新节点时，我们为其传递了第四个参数 refNode，当 refNode 存在时，我们应该使用 insertBefore 方法代替 appendChild 方法，这就需要我们修改之前实现的 mount 函数了 mountElement 函数，为它们添加第四个参数，如下：

// mount 函数
function mount(vnode, container, isSVG, refNode) {
  const { flags } = vnode
  if (flags & VNodeFlags.ELEMENT) {
    // 挂载普通标签
    mountElement(vnode, container, isSVG, refNode)
  }

  // 省略...
}

// mountElement 函数
function mountElement(vnode, container, isSVG, refNode) {
  // 省略...

  refNode ? container.insertBefore(el, refNode) : container.appendChild(el)
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

这样，当新 children 中存在全新的节点时，我们就能够保证正确的将其添加到容器元素内了。

:::tip
实际上，所有与挂载和 patch 相关的函数都应该接收 refNode 作为参数，这里我们旨在让读者掌握核心思路，避免讲解过程的冗杂。
:::

移除不存在的元素

除了要将全新的节点添加到容器元素之外，我们还应该把已经不存在了的节点移除，如下图所示：

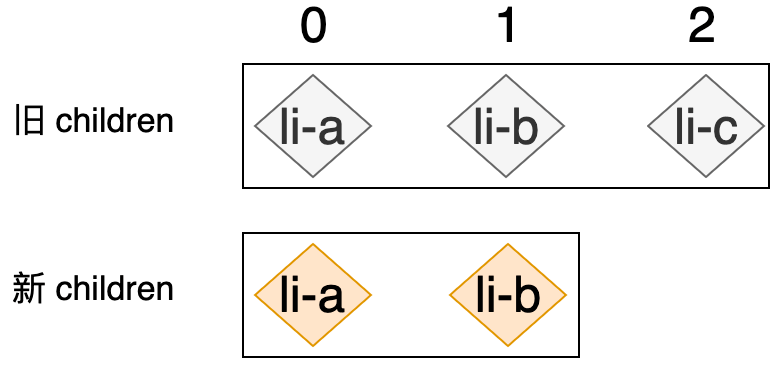
可以看出，新的 children 中已经不存在 li-c 节点了，所以我们应该想办法将 li-c 节点对应的真实 DOM 从容器元素内移除。但我们之前编写的算法还不能完成这个任务，因为外层循环遍历的是新的 children，所以外层循环会执行两次，第一次用于处理 li-a 节点，第二次用于处理 li-b 节点，此时整个算法已经运行结束了。所以，我们需要在外层循环结束之后，再优先遍历一次旧的 children，并尝试拿着旧 children 中的节点去新 children 中寻找相同的节点，如果找不到则说明该节点已经不存在于新 children 中了，这时我们应该将该节点对应的真实 DOM 移除，如下高亮代码所示：

let lastIndex = 0
for (let i = 0; i < nextChildren.length; i++) {
  const nextVNode = nextChildren[i]
  let j = 0,
    find = false
  for (j; j < prevChildren.length; j++) {
    // 省略...
  }
  if (!find) {
    // 挂载新节点
    // 省略...
  }
}
// 移除已经不存在的节点
// 遍历旧的节点
for (let i = 0; i < prevChildren.length; i++) {
  const prevVNode = prevChildren[i]
  // 拿着旧 VNode 去新 children 中寻找相同的节点
  const has = nextChildren.find(
    nextVNode => nextVNode.key === prevVNode.key
  )
  if (!has) {
    // 如果没有找到相同的节点，则移除
    container.removeChild(prevVNode.el)
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

至此，第一个完整的 Diff 算法我们就讲解完毕了，这个算法就是 React 所采用的 Diff 算法。但该算法仍然存在可优化的空间，我们将在下一小节继续讨论。