- 1离开华为,跳槽去银行科技岗!_华为程序员可以跳槽去哪
- 2Ubuntu18.04安装Tensorflow(GPU)及Keras_ubuntu keras tensorflow配置gpu
- 3hive创建数据库报错:Unable to instantiate org.apache.hadoop.hive.ql.metadata.SessionHiveMetaStoreClient_hive metastore client 没有权限创建数据库
- 47个Python爬虫小案例,人人都能用到,适合零基础小白!_python爬虫基础案例
- 5详细Ubuntu 22.04 配置最新UR机械臂仿真环境(ros2-humble, ur-sim, ur-ros2-driver)_using load_yaml() directly is deprecated. use xacr
- 6oracle guid 使用_oracle的函数guid函数
- 7基于微信小程序菜谱美食系统 (后台java+Springboot框架)答辩常规问题和如何回答(答辩指导)_java系统如何答辩
- 8AI嵌入式3——君正T40之MIPS32架构交叉编译opencv4篇_君正mips opencv mips-linux-gnu-gcc
- 9软考系统架构师知识点集锦八:嵌入式系统_软考 嵌入式系统 片级系统板级
- 10chromedriver和selenium的下载以及安装教程(114/116/117.....121版本)_chromedriver121
Pytorch深度学习笔记(五)反向传播算法_bp反向更新权重
赞
踩
目录
1.为什么要使用反向传播算法
简单模型可以使用解析式更新w
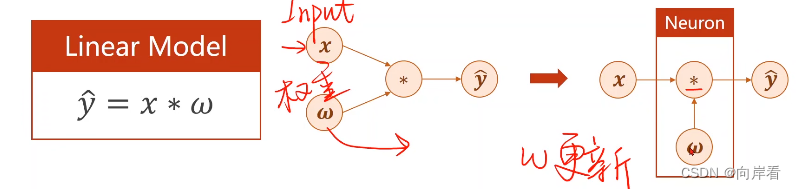
复杂模型,如图,输入矩阵为5*1矩阵,等一层权重矩阵H1为6*5矩阵,则需要30个解析式,第二层权重矩阵H2为6*7矩阵,则需要42个解析式,第三层……可以看出我们无法通过解析式的方式来更新w。

因此需要反向传播算法,反向传播算法可以在网络中传播梯度,最终通过链式法则完成每个节点的梯度计算,从而完成每个节点的w更新。
反向传播算法,又称 BP 算法,它将输出层的误差反向逐层传播,通过计算偏导数来更新网络参数使得误差函数最小化。
2.二层神经网络:

MM为矩阵乘法,ADD为矩阵加法,是预测值,w为权重,b为偏移量(bias)。

第一层H1为w1*x+b1,第二层H2为w2*H1+b2。
不难发现,如果一直进行线性变换,最终得到的化简函数依然是一个线性函数,因此需要在每一层的输出,引入一个的非线性的变换函数
。

3.反向传播算法更新权值的过程
根据链式法则可以向前推出前一个节点的偏导数,根据梯度向下算法的权重更新公式
=
-
,实现反向更新权重w。
(1) 一个计算图正向传播和反向传播的过程

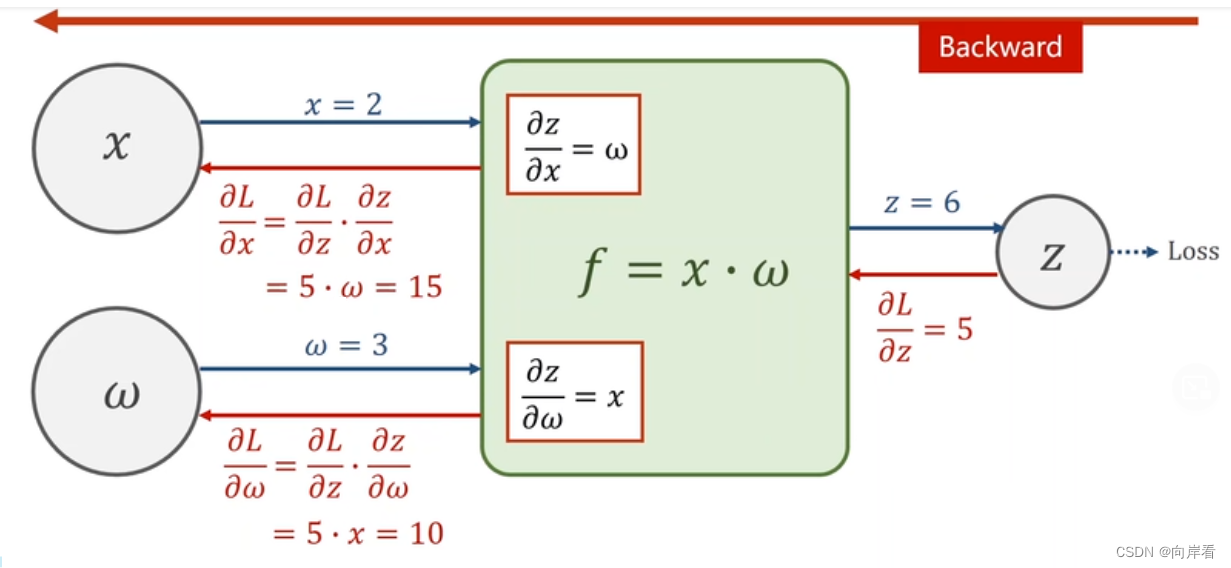
如图,根据链式法则,得到
,进行w更新。L为损失值Loss。
(2)具体实现过程
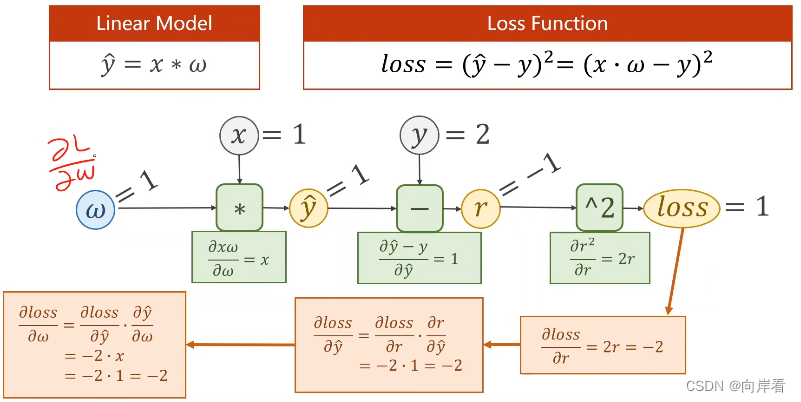
r为损失值loss。反向过程的最后,会得到
练习1:
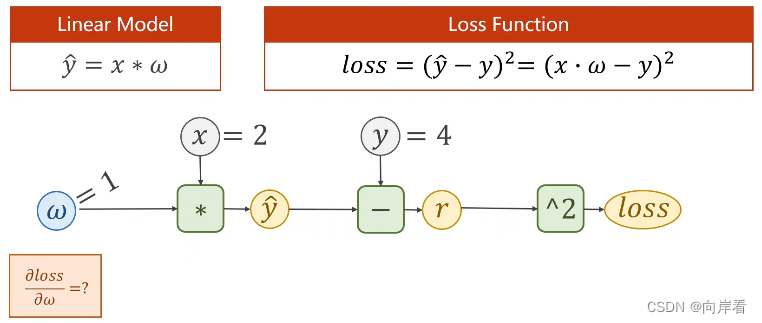
答案为-8
练习2:

答案为2 ,2
4.张量Tensor
单个元素叫标量(scalar),一个序列叫向量(vector),多个序列组成的平面叫矩阵(matrix),多个平面组成的立方体叫张量(tensor)。在深度学习中,标量、向量、矩阵、高维矩阵都统称为张量。在pytorch中,一个Tensor内部包含数据和导数两部分。

线性模型pytorch实现代码:
- import torch
-
- x_data = [1.0, 2.0, 3.0]
- y_data = [2.0, 4.0, 6.0]
-
- # 将w转化为一个只含一个标量的张量
- w = torch.Tensor([1.0])
- # 配置
- # 设置需要计算梯度
- w.requires_grad = True
-
- # 预测值函数
- def forward(x):
- return x * w
-
- # 误差值函数
- def loss(x, y):
- y_pred = forward(x)
- return (y_pred - y) ** 2
-
- print("predict (before training)", 4, forward(4).item())
- # 100轮的训练
- for epoch in range(100):
- for x, y in zip(x_data, y_data):
- # 先正向传播,生成计算图
- l = loss(x, y)
- # 再反向传播,backward()用于自动计算图中所有张量的梯度(偏导数)然后存入对应张量中的grad中
- l.backward()
- # item()函数的作用是从包含单个元素的张量中取出该元素值,并保持该元素的类型不变。grad是张量,使用item()进行取值,否则会生成计算图。
- # grad和data都是torch的属性,可以直接调用
- print('\tgard:', x, y, w.grad.item())
- # 更新w的值。注意grad也是一个张量,包含data和梯度。
- # grad是张量,grad.data取到其data,grad.data不会计算图
- w.data = w.data - 0.01 * w.grad.data
- # 将w的梯度值清零
- w.grad.data.zero_()
- # 注意l也是张量,需要使用item()取值
- print("progress:", epoch, l.item())
-
- print("predict (after training)", 4, forward(4).item())
-
-

backward():用于自动计算图中所有张量的梯度(偏导数)然后存入对应张量中的grad中
item():用于从包含单个元素的张量中取出该元素值,并保持该元素的类型不变
w.grad.data.zero_():将w的梯度值清零,防止累积造成空间浪费
grad和data都是torch的属性,可以直接调用
注意:grad也是一个张量。grad.data取到其data,grad.data不会生成计算图,使用item()有等同效果。
练习(代码实现):

矩阵手册:http://faculty.bicmr.pku.edu.cn/~wenzw/bigdata/matrix-cook-book.pdf


