【蓝桥杯经典数学题】杨辉三角形

杨辉三角一图览

			  			1
					1		1
				1		2      1
			1       3	    3      1
		1		4		6		4 		1
	1		5		10		10		5		1
1		6		15		20		15		6		1
1
2
3
4
5
6
7

前言

由图可知杨辉三角具有对称性，很多时候可以折半计算，节省时间
同时我们可以以排列组合的方式将杨辉三角展现出来

借个图先

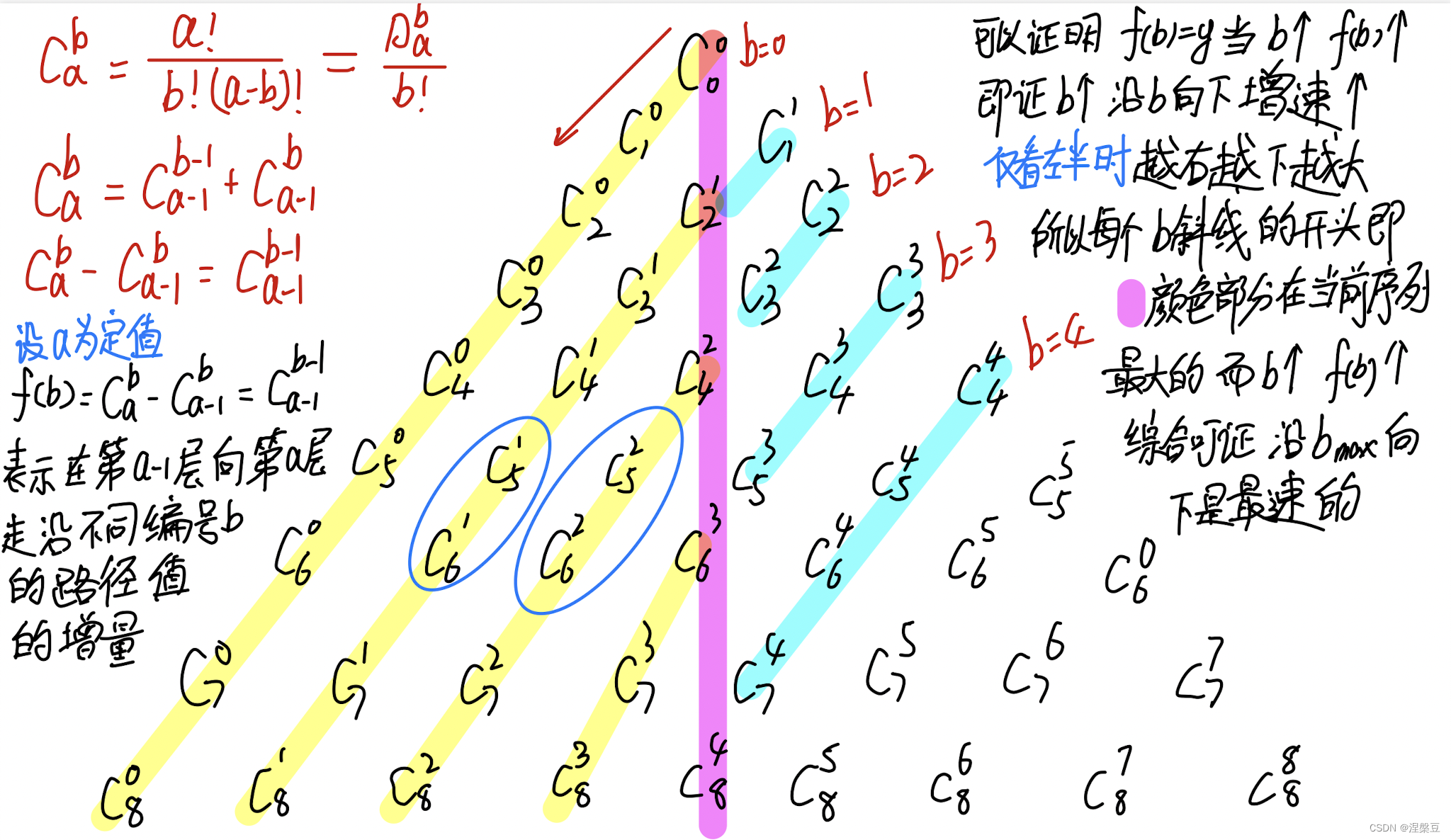
求杨辉三角任意一行

我们在编程界中经常把排列组合中的公式用A（a,b），C(a,b)表示
比如C（5,2） = 10
那么对n-1行的公式可以写成
C（n，r） = （n-r + 1）/ r * C(n,r-1);
杨辉三角的每一行初始值为C(n,0) = 1

又根据杨辉三角的对称性，我们可以折半计算，在计算中心轴左边的值的同时也能将右边的值算出来

该公式的应用
lP1118 [USACO06FEB]Backward Digit Sums G/S

代码

#include <iostream>

using namespace std;

const int N = 30;

int n,sum;
bool st[N];
int a[N];
int delta[N];

void getdelta()
{
	delta[0] = delta[n-1] = 1;
	
	if(n > 1)
	{
		for(int i = 1;i*2 <= n;++i)
			delta[i] = delta[n-i-1] = (n-i) * delta[i-1]/i;
	}
} 

bool dfs(int u,int num,int v)
{
	if(v > sum) return false;
	
	if(u == n)
	{
		if(v == sum)
		{
			a[u] = num;
			return true;
		}
		return false;
	}
	
	st[num] = true;
	
	for(int i = 1;i <= n;++i)
	{
		if(!st[i] && dfs(u + 1,i,v + delta[u] * i))
		{
			a[u] = num;
			return true;
		}
	}
	st[num] = false;
	
	return false;
}
int main()
{
	cin>>n>>sum;
	
	getdelta();//得到第n层杨辉三角 
	
	if(dfs(0,0,0)) for(int i = 1;i <= n;++i) cout<<a[i]<<' ';
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

求杨辉三角某一值起始位置

经过多数人的研究，已经找到了一种非常精妙的方法来快速确定任意值的起始位置，所耗时间只需4ms

首先再看一次图

			  			1
					1		1
				1		2      1
			1       3	    3      1
		1		4		6		4 		1
	1		5		10		10		5		1
1		6		15		20		15		6		1
1
2
3
4
5
6
7

我们可以将杨辉三角的右半边删掉，因为杨辉三角的对称性，显而易见我们能推导出任意值的起始位置一定在左半边

			  			1
					1		
				1		2      
			1       3	    
		1		4		6		
	1		5		10	
1		6		15		20	
1
2
3
4
5
6
7

得到该图后我们发现，我们可以通过斜行位置与行位置来确定某一值
假设起始行数与斜行都为0
比如我们求C（6,3），组合数C（6,3） = 20
该过程代码

long long C(int a, int b) //C(a,b)
{
   long long res = 1;
   for (int i = a, j = 1;j <= b;--i, ++j)
   {
   		res = res * i / j;
   }
   return res;
}

1
2
3
4
5
6
7
8
9
10

同时我们可以确定，这一斜行找到的值的位置，总会比他上面一个斜行找到同一值的位置要小
因此我们可以倒着枚举每一斜行来寻找某一值，找到的位置一定是起始位置

而且每一斜行k的起始行数n，总有一种规律 2*k = n

现在我们总结一下前面找到的规律
1.通过斜行与行的位置可以推断某一值
2.倒着枚举每一斜行可以找到该值的第一次出现位置
3.斜行k * 2 = 斜行起始行数n
4.由123点我们可以通过二分查找行来寻找该值，起始行为2*k，终点行为n（选择n是因为n足够大）
补充一点，如果已知某一行数n，可以推断该行之前总共有C（n，2）个数，在把斜行看做列，即可得到某一值的位置公式

pos = (n + 1）*n / 2 + k +1;
1

例题
P8749 [蓝桥杯 2021 省 B] 杨辉三角形
实现代码

#include <iostream>

using namespace std;

long long n;

long long C(int a, int b) //C(a,b)
{
	long long res = 1;
	for (int i = a, j = 1;j <= b;--i, ++j)
	{
		res = res * i / j;
		if (res > n) return res;//防止超过n直接爆long long，提前退出
	}
	return res;
}
int main()
{
	cin >> n;

	if (n == 1)//因为C（2,1）不存在，需要特判
	{
		cout << 1 << endl;
		return 0;
	}
	for (int i = 16;i >= 1;--i)
	{
		long long l = 2 * i, r = max(l, n);//有可能l比n大

		while (l < r)//二分查找左端点
		{
			long long mid = (l + r) >> 1;
			if (C(mid, i) < n) l = mid + 1;
			else r = mid;
		}

		if (C(l, i) == n)
		{
			cout << (l + 1) * l / 2 + i + 1 << endl;
			return 0;
		}
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45