【论文阅读笔记】Myers的O(ND)时间复杂度的高效的diff算法_an o(nd) difference algorithm and its variations

前言

之前咱们三个同学做了个Simple-SCM，我负责那个Merge模块，也就是对两个不同分支的代码进行合并。当时为了简便起见，遇到文件冲突的时候，就直接按照文件的更改日期来存储，直接把更改日期较新的那个文件认为是我们要保留的文件版本。但是这样子做是存在很多问题的，因为这样做就无法对不同分支的代码他们各自的特性进行整合，最终保留的只是其中一个分支的代码。因此，加入按行进行比较的diff算法是非常必要的。

然后，本着自力更生的理念，我希望能够自己写出这个代码，然后把它应用到Simple-SCM之中。今年五月份的时候就看到了Google开源的diff-match-patch库，这里面提供了完善的diff功能。一看代码量，三千多行，就把这事往后推了。这个开源库里面讲到了，用的就是Myers的论文，我就想，我能不能自己阅读论文，把它复现出来呢？但是由于时间的缘故，就没去搞。毕竟当时是实训大作业要赶ddl嘛，先把软件做出来再说。

到了最近，我又找到了这个库，然后想起了还没有完成的Merge模块，就想着去把它做出来。于是，我说干就干，还深夜发了一条朋友圈，来立一个Flag。

然后我就，真的，抽空把这个论文给看了。并且把它的基础版本给复现了出来！（论文原文请转到文末）

什么是diff？

diff在软件开发过程中非常常见，最直观的就是在git里面，可以查看两个不同版本的代码的区别。得出的数据包括了：新增的、删除的、修改的、没有改变的。

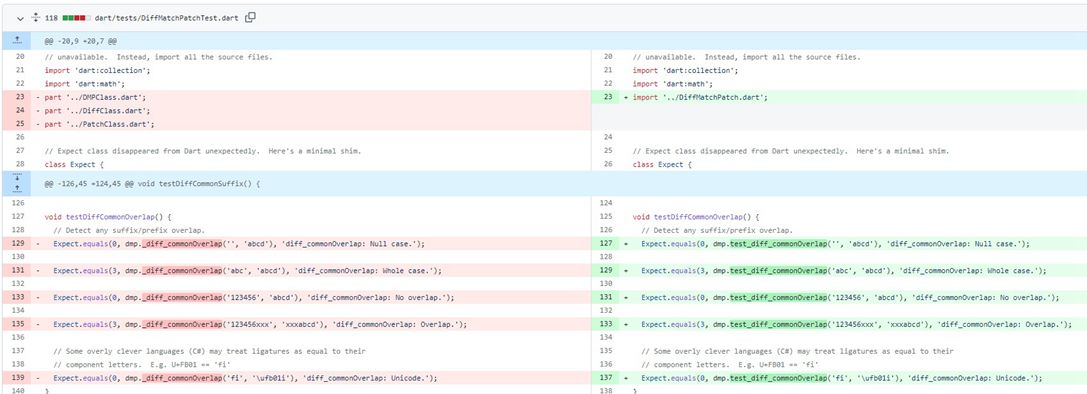
在Github上查看代码版本之间的差异

上面这张图展现的就是在Github上看到的，展现了两个版本的代码之间的差异。红色的表示这段代码在新版中已经被删除了，绿色的表示是新增的，其中，颜色加深部分则是发生改变的。

并且，左边的旧版本代码有很多种方式来变成右边的新版代码。找到一个最符合人类直观反应的diff，也是一个复杂的问题。

Myers的Diff算法的原理

我们如何判断两份代码文件的差异呢？首先我们要认识到它是字符串，换行只是加了换行符而已。因此，从本质上来说，我们要能够判断两个字符串的差异。

这就回归到了我们熟知的最长公共子序列（LCS）问题了，对于LCS问题，在之前我也学过LCS的算法。之前学的基于DP的算法的时间复杂度是O(MN)，也就是我们所说的N平方复杂度。对于大量的数据而言，之前的算法速度是很慢的。

编辑图

因此，Myers在论文中引入了编辑图(Edit Graph)的概念。也就是将旧字符串放在x轴，新字符串放在y轴。起点是(0,0)，终点是(M,N)。

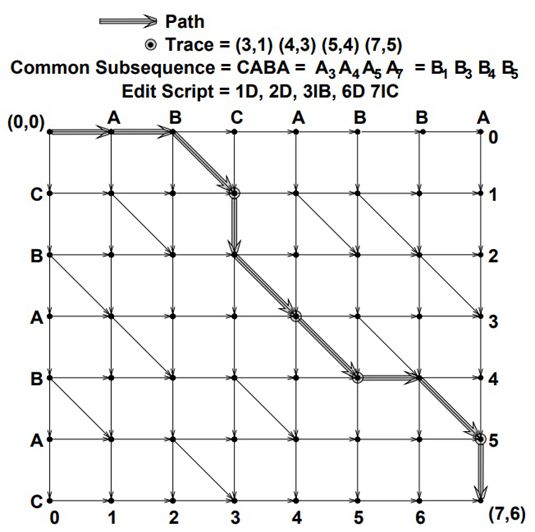
编辑图

编辑图具有横向边、纵向边以及对角边。这些边都是有向的，只能向右、向下和向右下角。

这三种边有其特定的含义：

• 横向边：代表删除对应的旧字符串的字符
• 纵向边：代表从新字符串中插入一个字符到旧串的当前位置中。
• 对角边：新旧字符串中相同的部分。

然后，我们的目标就是，把旧字符串经过最少、最直观的变换，使其变成新字符串。转换到编辑图上，就是经过最短的、最多连续的一条路径，从(0,0)点走到(M,N)点。也就是SES问题（最短编辑图问题）

由于横向边和纵向边的出现意味着我们对字符串进行了编辑，而对角边则意味着没有编辑这个字符串。因此我们将横向边和纵向边的权值设置为1，对角边的权值设置为0. 那么，这个diff的问题就进一步转化为单源最短路径的问题了。

当时我看到这里，就想着用狄克斯特拉算法来求这个单源最短路径问题了。

但是！千万不要这么做！

（不然这篇文章就结束了）

狄克斯特拉算法确实可以求解SES问题，但是它却不能求解出“最直观”的变换。它求出来的编辑图虽然满足最短路，但是不一定满足“边的最连续”。而且，狄克斯特拉算法哪怕经过了优先级队列的优化，时间复杂度达到了O(ElogE)，但是这个仍然比Myers的算法的时间复杂度高。原因在于狄克斯特拉算法在应用到diff问题上时，没有利用到两个字符串的diff的性质。

定义：D-path指的是，横向边纵向边之和为D的路径

因此，0-path指的就是，全为对角边的路径。

如何标记对角边？

由于对角边是与x、y轴都成45°的，因此，我们只要知道其截距k，就能表示任意一条对角边。故有：

x-y=k

我们用k来给对角边编号，那么对角边的编号范围就是[-M,N]

两项引理

引理1：一条D-path的终点必须在对角边k∈[-D, -D+2,…,D-2, D]上

这其实很好理解，经过D次编辑，那么最远就只能到达第±D条对角边。并且由于折返的原因，从最远处，每次缩短一节，对应的对角边的编号就减2.这个画个图可以很好理解。

引理2：这个有点长，我就不翻译了，大家自己看看。

引理2

A furthest reaching 0-path ends at (x,x), where x is min( z−1 || a z ≠bz or z>M or z>N). A furthest reaching D-path on diagonal k can without loss of generality be decomposed into a furthest reaching (D − 1)-path on diagonal k − 1, followed by a horizontal edge, followed by the longest possible snake or it may be decomposed into a furthest reaching (D − 1)-path on diagonal k+1, followed by a vertical edge, followed by the longest possible snake

大概意思就是，d-path可以由(D-1)-path转移而来。这也为我们后面的计算提供了依据。

关于上面两项引理的证明，有兴趣的读者可以查阅论文原文的第五页，即可看到证明。

算法思路

Myers的diff算法是贪心的、使用了动态规划的思想的。我们既然要得到到达点(M,N)的最短路径，设到达点(M,N)的路径长度为D，那就是要先得到众多(D-1)-path，然后从这些备选路径的结束点为起点，计算出到达点(M,N)最直观最短的一条路径，这就是我们要连上去的路径。

因此，我们只需要从0-path开始，迭代的计算1-path，2-path，3-path，…，D-path。这样，我们求到的第一条能到达点(M,N)的路径，就是答案了。也就是我们的编辑路径。我们的diff就找到了。

上面两段讲了一个总体的思路，现在就放论文里面的伪代码上来，让读者更加直观地了解到这个算法的工作流程。

The Greddy LCS/SES Algorithm

上述伪代码中，数组V存储的是D-path在不同的对角边上能到达的最远的顶点的x值。

由于其下标可以是负数，因此我们可以把负下标映射到数组的高地址端，从高地址端向下生长，来实现负下标的功能。

自己的一些感悟

这次借着这个机会，看了英文原版的论文，把算法给复现了出来。算法本身不是特别的难，我觉得在这个过程中，我最大的收获在于，学会了看论文。这个只能说是刚刚会看，真正的对论文的深入思考和批判，我还做不到，这也是我需要提高的。在阅读的过程中，也深刻体会到了，英文的重要性。语言的问题是很大的阅读障碍，这个问题确实得重视。就像我逛GitHub和StackOverflow的时候的感觉一模一样，全英的，机器翻译也超不通顺，看着好辛苦。这个阅读能力真的得不断的提升。

然后，这个算法我目前只是把它复现出了基础版本，后面的线性空间优化还有一些变种，我还没有时间去看，这个也会继续去看，继续更新下去。

然后最初我说，要自己做一个difflib出来，现在想了想，确实不那么容易。因为要按行为单位来计算diff，要得到“原来存在，只是更改了一些”这类信息，还涉及到了相似度的计算的问题。确实不是那么的简单。于是，我决定，还是用Google的开源库来实现Simple-SCM的Merge吧。确实人家造的轮子还是很不错的。我这算是打脸了，我承认我的技术还不行，也没有这么多时间去钻研这个diff，把它做成difflib。这个我以后还要加油，说不定哪天真的能自己写一个了呢？

附件：基础版代码

#include <bits/stdc++.h>
 
using namespace std;
 
 
int get_index(int maxn, int idx) {
    if (idx >= 0)
        return idx;
    else
        return (maxn << 1) + idx;
 
}
 
struct Snake {
    Snake() = default;
 
    Snake(int sx, int sy, int mx, int my, int ex, int ey) {
        start_x = sx;
        start_y = sy;
        mid_x = mx;
        mid_y = my;
        end_x = ex;
        end_y = ey;
    }
 
    int start_x, start_y, end_x, end_y;
    int mid_x, mid_y;
};
 
struct point {
    point(int xx, int yy) {
        x = xx, y = yy;
    }
 
    int x, y;
 
    bool operator==(const point &p) const {
        if (x == p.x && y == p.y)
            return true;
        else
            return false;
    }
 
    bool operator!=(const point &p) const {
        if (*this == p)
            return false;
        else
            return true;
    }
};
 
void MyersDiff(string a, string b) {
    vector<vector<Snake>> ans;
    const int MAXN = a.length() + b.length();
    int *V = new int[2 * MAXN + 1];
    memset(V, 0, sizeof(int) * (2 * MAXN + 1));
    V[1] = 0;
    for (int d = 0; d <= MAXN; ++d) {
        printf("D:%d\n", d);
 
        vector<Snake> tmp;
        bool flag = false;
        for (int k = -d; k <= d; k += 2) {
            int start_x, start_y;
            bool down = false;
            if (k == -d || (k != d && V[get_index(MAXN, k - 1)] < V[get_index(MAXN, k + 1)]))
                down = true;
                //start_x = V[get_index(MAXN,k+1)];
            else
                down = false;
            //start_x = V[get_index(MAXN,k-1)]+1;
 
            int kPrev = down ? (k + 1) : (k - 1);
 
            start_x = V[get_index(MAXN, kPrev)];
            start_y = start_x - kPrev;
            int mid_x = down ? start_x : (start_x + 1);
            int mid_y = mid_x - k;
 
            int end_x = mid_x, end_y = mid_y;
 
            int snake = 0;
            while (end_x < a.length() && end_y < b.length() && a[end_x] == b[end_y]) {
                ++end_x;
                ++end_y;
                ++snake;
            }
 
            V[get_index(MAXN, k)] = end_x;
            tmp.emplace_back(Snake(start_x, start_y, mid_x, mid_y, end_x, end_y));
            printf("start:(%d,%d),  mid:(%d,%d),  end:(%d,%d)\n", start_x, start_y, mid_x, mid_y, end_x, end_y);
 
            if (end_x >= a.length() && end_y >= b.length()) {
                //found
                printf("Found.\n");
                flag = true;
                break;
            }
        }
        ans.emplace_back(tmp);
        if (flag)
            break;
    }
 
    delete[] V;
    cout << ans.size() << endl;
    //处理得到路径
    int end_x = a.length(), end_y = b.length();
    stack<point> st;
    for (auto ptr = ans.end() - 1; ptr >= ans.begin(); --ptr) {
        auto tmp = *ptr;
        Snake tmps;
        for (auto p: tmp) {
            if (p.end_x == end_x && p.end_y == end_y) {
                tmps = p;
                auto tmpp = point(p.end_x, end_y);
                if (st.empty() || st.top() != tmpp)
                    st.push(tmpp);
 
                tmpp = point(p.mid_x, p.mid_y);
                if (st.empty() || st.top() != tmpp)
                    st.push(tmpp);
                end_x = p.start_x, end_y = p.start_y;
                break;
            }
        }
    }
 
    while (!st.empty()) {
        const auto tmpp = st.top();
        st.pop();
        printf("(%d,%d)==>", tmpp.x, tmpp.y);
    }
 
 
    printf("done\n");
}
 
int main() {
 
    string a = "XBCAC";
    string b = "ABBAC";
    MyersDiff(a, b);
}

References

EUGENE W. MYERS “An O(ND) Difference Algorithm and Its Variations”  https://neil.fraser.name/writing/diff/myers.pdf

转载请注明来源：【论文阅读笔记】Myers的O(ND)时间复杂度的高效的diff算法 | 龙进的博客