经典网络解（三） 生成模型VAE | 自编码器、变分自编码器|有监督，无监督_vae生成网络详解

之前我们的很多网络都是有监督的

生成网络都是无监督的（本质就是密度估计），我们首先来讲有监督学习，无监督学习

1 有监督与无监督

有监督学习

目标学习X到Y的映射，有正确答案标注

示例

分类回归

目标检测

语义分割

无监督学习

没有标记，找出隐含在数据里的模型或者结构

示例

聚类

降维 1 线性降维：PCA主成分分析 2 非线性降维：特征学习（自编码）

密度估计

当谈论有监督学习和无监督学习时，你可以将其比喻为烹饪和探险两种不同的方式：

有监督学习就像是在烹饪中的烹饪食谱。你有一本详细的烹饪书（类似于带标签的训练数据），书中告诉你每一步应该怎么做，包括每个食材的量和准备方式（就像标签指导模型的输出）。你只需按照指示的步骤执行，最终会得到一道美味的菜肴。在这个过程中，你不需要创造新的食谱，只需遵循已有的指导。

无监督学习则类似于一场探险，你被带到一个未知的地方，没有地图或导航，只有一堆不同的植物和动物（类似于未标记的数据）。你的任务是探索并发现任何可能的规律、相似性或特征，以确定它们之间的关系（就像从未标记的数据中发现模式）。在这个过程中，你可能会发现新的物种或新的地理特征，而无需事先知道要找什么。

2 生成模型

学习训练模型的分布，然后产生自己的模型！给定训练集，产生与训练集同分布的新样本！

生成模型应用

​ 图像合成 图像属性编辑 图片风格转移等

2.1 重要思路

显示密度估计

​ 显示定义并求解分布

​ 又可以分为

1 可以求解的

PixelRNN

2 不可以求解的

VAE

隐示密度估计：学习一个模型，而无需定义它

GAN

3 VAE

变分自编码器

我们先介绍自编码器和解码器

编码器

编码器的作用一般都是提取压缩特征，降低维度，保证数据里最核心最重要的信息被保留

解码器

但是只有编码器是不行的，我不知道编码器提取的特征怎么样，所以我们需要加上解码器，解码器就可以利用提取到的特征进行重构原始数据，这样的话重构出来的图像越像原图说明编码器越好

编码器怎么单独用？

做分类或其他有监督任务

对于输入数据，利用编码器提取特征，然后输出预测标签，根据真实标签进行计算损失函数，微调网络，这种情况可以适用于少量的数据标记情况

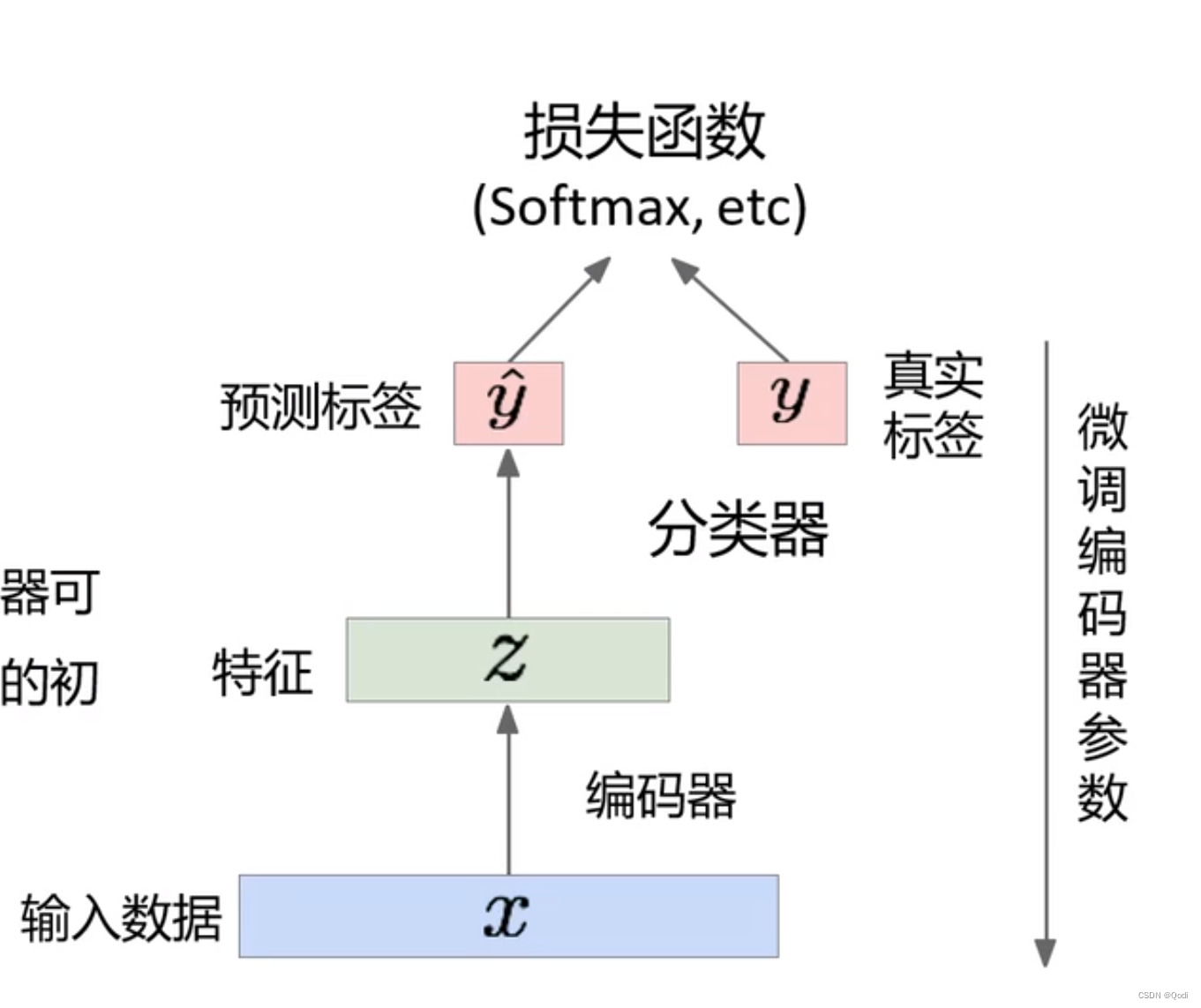
但是这样的效果往往不如在有监督网络微调的方式

解码器怎么单独用？

做图像生成

比如给一个随机的二维编码，我就可以生成一个真实图像样本

讲完了编码器解码器，我们想问为什么要用变分？变分是什么

为什么要用变分

上面的我的自编码器的思想太死板了！他只能学到一些离散的编码，学到自己见过的内容，无法组合创新

VAE引入了概率分布的概念，它假设数据的潜在表示（潜在空间）是连续的，并使用概率分布来建模这个潜在空间。具体来说，VAE假设潜在表示服从一个潜在空间的高斯分布，其中编码器学习生成均值和方差，而解码器从这个分布中采样。这种建模方式允许VAE学习数据的连续、平滑的表示，而不仅仅是对数据的离散编码。

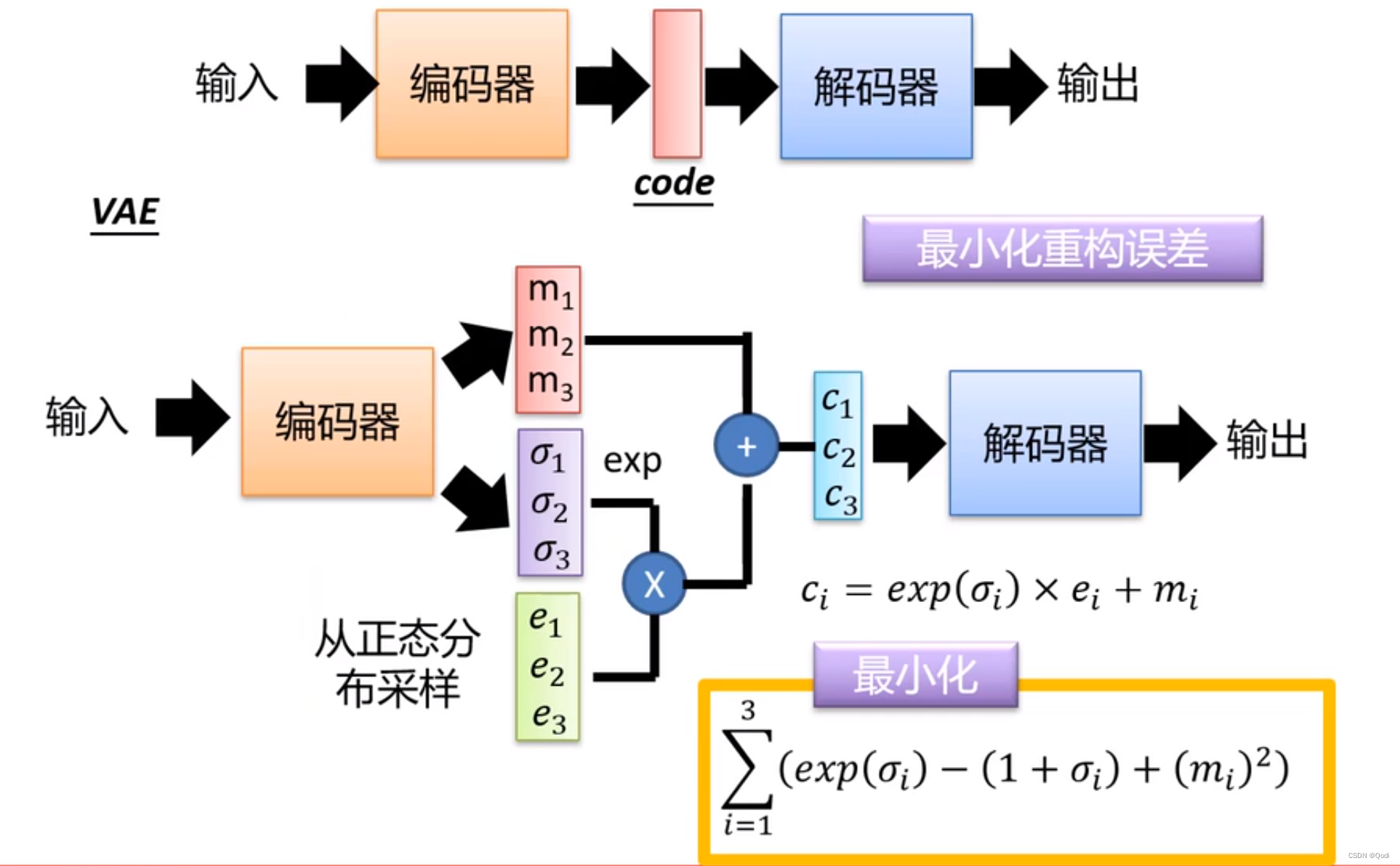
自编码器输入图像后，编码器会生成一个编码

而如图所示变分自编码器是输入图片，编码器输出一个分布（均值和方差）

生成图像的时候，从这个分布中采样送入解码器即可

两个损失函数

一个最小化重构误差

一个尽可能使得潜在表示的概率分布接近标准正态分布使得0均值1方差（损失函数一方面可以避免退化成自编码器，另一方面保证采样简单）

变分自编码器推导

高斯混合模型

用很多个简单高斯逼近最后的比较复杂的分布

优化解码器参数使得似然函数L最大， 但是实际中由于有隐变量的存在而无法积分，所以我们只能通过近似的方式

具体推导可以查看如下这篇博客

从零推导：变分自编码器（VAE） - 知乎 (zhihu.com)

4 代码实现

import torch
import torch.nn as nn
import torch.nn.functional as F

class VAE(nn.Module):
    def __init__(self, input_dim, hidden_dim, latent_dim):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc21 = nn.Linear(hidden_dim, latent_dim)
        self.fc22 = nn.Linear(hidden_dim, latent_dim)
        self.fc3 = nn.Linear(latent_dim, hidden_dim)
        self.fc4 = nn.Linear(hidden_dim, input_dim)
        
    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        mu = self.fc21(h1)
        log_var = self.fc22(h1)
        return mu, log_var
    
    def reparameterize(self, mu, log_var):
        std = torch.exp(0.5*log_var)
        eps = torch.randn_like(std)
        z = mu + eps*std
        return z
    
    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        recon_x = torch.sigmoid(self.fc4(h3))
        return recon_x
    
    def forward(self, x):
        mu, log_var = self.encode(x)
        z = self.reparameterize(mu, log_var)
        recon_x = self.decode(z)
        return recon_x, mu, log_var

# 定义损失函数，通常使用重建损失和KL散度
def loss_function(recon_x, x, mu, log_var):
    BCE = F.binary_cross_entropy(recon_x, x, reduction='sum')
    KLD = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
    return BCE + KLD

# 创建VAE实例并进行训练
input_dim = 784  # 用于示例的MNIST数据集
hidden_dim = 400
latent_dim = 20
vae = VAE(input_dim, hidden_dim, latent_dim)

# 定义优化器
optimizer = torch.optim.Adam(vae.parameters(), lr=1e-3)

# 训练VAE
def train_vae(train_loader, vae, optimizer, num_epochs):
    vae.train()
    for epoch in range(num_epochs):
        for batch_idx, data in enumerate(train_loader):
            data = data.view(-1, input_dim)
            recon_batch, mu, log_var = vae(data)
            loss = loss_function(recon_batch, data, mu, log_var)
            
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            if batch_idx % 100 == 0:
                print(f'Epoch [{epoch+1}/{num_epochs}], Batch [{batch_idx+1}/{len(train_loader)}], Loss: {loss.item()}')

# 使用MNIST数据集示例
from torchvision import datasets, transforms
from torch.utils.data import DataLoader

transform = transforms.Compose([transforms.ToTensor()])
train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=4)

num_epochs = 10
train_vae(train_loader, vae, optimizer, num_epochs)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78