扩散模型长期以来一直受到可扩展性和二次复杂性问题的困扰，特别是在基于 Transformer 的结构中。在这项研究中，我们旨在利用名为 Mamba 的状态空间模型（State-Space Model）的长序列建模能力，将其适用性扩展到视觉数据生成领域。首先，我们确定了大多数当前基于 Mamba 的视觉方法中的一个关键缺失，即在 Mamba 的扫描方案中缺乏对空间连续性的考虑。其次，基于这一观察结果，我们引入了一种简单的、即插即用、零参数的方法，名为 Zigzag Mamba，它优于基于 Mamba 的基准线，并展现了与基于 Transformer 的基准线相比更好的速度和内存利用率。最后，我们将 Zigzag Mamba 与随机插值（Stochastic Interpolant）框架结合起来，探讨了该模型在大分辨率视觉数据集上的可扩展性，如 FacesHQ 1024 × 1024、UCF101、MultiModal-CelebA-HQ 和 MS COCO 256 × 256。

项目页面：https://taohu.me/zigma/

1. 简介

状态空间模型 [30,31,34] 显示出在长序列建模方面具有巨大潜力，与基于 Transformer 的方法竞争。已经提出了几种方法 [26,29,31,70] 来增强状态空间模型的鲁棒性 [93]、可扩展性 [29] 和效率 [31,32]。其中一种名为 Mamba 的方法 [29] 旨在通过工作高效的并行扫描和其他数据相关的创新来缓解这些问题。然而，Mamba 的优势在于 1D 序列建模，将其扩展到 2D 图像是一个具有挑战性的问题。先前的工作 [59,98] 通过计算机层次结构（computer hierarchy）（例如行列主序，row-and-column-major order）来直接将 2D 标记扁平化，但这种方法忽视了空间连续性，如图 1 所示。其他工作 [56,62] 考虑了单个 Mamba 块中的各个方向，但这引入了额外的参数和 GPU 内存负担。在本文中，我们旨在强调 Mamba 中空间连续性的重要性，并提出了几种直观简单的方法，通过在图像中引入基于连续性的归纳偏差，使 Mamba 块能够应用于 2D 图像。我们还将这些方法推广到具有空间-时间分解的 3D 序列。

随机插值 [3] 提供了一个更一般化的框架，可以统一各种生成模型，包括归一化流（Normalizing Flow） [14]、扩散模型 [38,71,73]、流匹配（Flow matching） [4,54,58] 和薛定谔桥（Schrödinger Bridge） [55]。以前，一些工作 [63] 在相对较小的分辨率上，例如 256×256、512×512 上探索了随机插值。在这项工作中，我们旨在进一步探索更复杂的情景，例如 1024×1024 分辨率甚至视频中的情况。

2. 相关工作

Mamba。几项研究 [83,84] 表明，在某些条件下，状态空间模型具有普适逼近能力。作为一种新的状态空间模型，Mamba 具有有效建模长序列的优越潜力，在医学影像学 [62,69,87,90]、图像恢复 [33,97]、图（graph） [10]、NLP 词字节 [81]、表格数据 [2]、点云 [52] 和图像生成 [24] 等各个领域已经得到探索。其中，与我们最相关的是 VisionMamba [59,98]、S4ND [64] 和 Mamba-ND [51]。

VisionMamba [59,98] 在判别任务中使用双向 SSM，这会带来很高的计算成本。我们的方法将简单的替代性 Mamba 扩散应用于生成模型。
S4ND [64] 在 Mamba 的推理过程中引入了局部卷积，超越了仅使用 1D 数据的情况。
Mamba-ND [51] 在判别任务中考虑了多维度，利用单个块内的各种扫描。

相比之下，我们的重点是将扫描复杂性分布到网络的每一层，从而最大程度地利用零参数负担的视觉数据归纳偏差。

扩散模型中的主干。扩散模型主要采用基于 UNet 的 [38,68] 和基于 ViT 的 [8,66] 主干。虽然 UNet 以高内存需求著称 [68]，但 ViT 受益于可扩展性 [15,21] 和多模态学习 [9]。然而，ViT 的二次复杂性限制了视觉标记处理的范围，促使研究朝着缓解这一问题的方向进行 [11,19,85]。

受到 Mamba [29] 的启发，我们的工作探索了基于 SSM 的模型作为通用扩散主干，保留了 ViT 的模态无关性和序列建模优势。
与此同时，DiffSSM [91] 关注 S4 模型 [31] 内的无条件和类别条件。
DIS [24] 主要探索了相对较小规模上的状态空间模型，这并不是我们工作的确切重点。

我们的工作与他们的工作有很大不同，因为我们的工作主要集中在使用 Mamba 块进行主干设计，并将其扩展到文本条件。此外，我们将我们的方法应用于更复杂的视觉数据。

3. 方法

在本节中，我们首先提供状态空间模型 [30,31,34] 的背景信息，特别关注一种称为 Mamba [29] 的特殊情况。然后，我们重点介绍了 Mamba 框架内的空间连续性关键问题，并基于这一洞见提出了Zigzag Mamba。这一改进旨在通过将 2D 数据中固有的连续性归纳偏差纳入模型，提高 2D 数据建模的效率。此外，我们设计了一个基本的交叉注意力块，用于在 Mamba 块上实现文本条件。随后，我们建议通过将模型分解为空间和时间维度，将这种方法扩展到 3D 视频数据，从而促进建模过程。最后，我们介绍了用于训练和采样的随机插值的理论方面，这些理论支撑着我们的网络架构。

3.1 背景：状态空间模型

（2024，DiS，扩散，状态空间主干，Mamba）具有状态空间主干的可扩展扩散模型

（2024，VMamba，交叉扫描，线性复杂度，全局感受野，动态权重）视觉状态空间模型

（2023|ICCV，DiT，扩散 transformer，Gflops）使用 Transformer 的可扩展扩散模型

3.2 扩散主干：Zigzag Mamba

DiT 风格网络。我们选择使用 AdaLN [66] 的 ViT 框架，而不是以跳跃层为重点的 U-ViT 结构 [8]，因为 ViT 已经在文献中被证明是一种可扩展的结构 [9,15,65]。考虑到上述观点，它指导了我们在图 4 中所示的 Mamba 网络设计。这一设计的核心组件是 Zigzag 扫描（Zigzag Scanning），将在下文中进行解释。

Mamba 中的 Zigzag 扫描。先前的研究 [82,91] 在 SSM 框架内使用了双向扫描。这种方法已经扩展到包括额外的扫描方向 [56,59,92]，以考虑 2D 图像数据的特性。这些方法将图像块沿四个方向展开，得到四个不同的序列。然后，每个序列通过每个 SSM 一起处理。然而，由于每个方向可能具有不同的 SSM 参数（A、B、C 和 D），增加方向的数量可能会导致内存问题。在这项工作中，我们探讨了将 Mamba 的复杂性摊销到网络的每一层的潜力。

我们的方法围绕着在将它们馈送到前向扫描块之前对 token 进行重新排列的概念。对于来自第 i 层的给定输入特征 zi，重排列后的前向扫描块的输出特征 z_(i+1) 可以表示为：

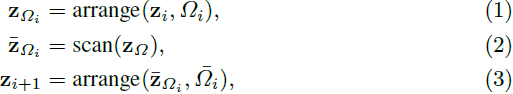
Ωi 代表第 i 层的 1D 置换（permutation），它通过 Ωi 重新排列 patch token 的顺序，¯Ωi 代表逆重排操作。这确保 zi 和 z_(i+1) 都保持了原始图像 token 的采样顺序。

现在我们探讨 Ωi 操作的设计，考虑到从 2D 图像中引入的额外归纳偏差。我们提出了一个关键属性：空间连续性。关于空间连续性，当前 Mamba 在图像中的创新 [56,59,98] 通常按照计算机层次结构，比如行和列主序，直接压缩 2D patch token。然而，这种方法可能不够优化，无法有效地将归纳偏差与相邻 token 结合起来，如图 3 所示。为了解决这个问题，我们引入了一种新颖的扫描方案，旨在在扫描过程中保持空间连续性。此外，我们考虑了空间填充（space-filling），这意味着对于大小为 N×N 的 patch，1D 连续扫描方案的长度应为 N^2。这有助于有效地将 token 整合起来，以最大限度地发挥 Mamba 块内长序列建模的潜力。

为了实现上述属性，我们启发式地设计了八种可能的空间填充连续方案，表示为 Sj（其中j∈[0,7]），如图 3 所示。虽然可能存在其他可想象的方案，但为了简单起见，我们将使用限制在这八种方案上。因此，每一层的方案可以表示为 Ωi = S_{i%8}，其中 % 表示 mod 运算符。

在 Zigzag Mamba 上部署文本条件。尽管 Mamba 提供了有效的长序列建模优势，但这是以牺牲注意机制为代价的。因此，对于基于 Mamba 的扩散模型，对于文本条件的整合探索有限。为了填补这一空白，我们提出了一个简单的交叉注意力块，建立在 Mamba 块之上，并带有跳跃层，如图 4 所示。这种设计不仅能够实现长序列建模，还能促进多 token 条件，比如文本条件。此外，它还具有提供可解释性的潜力，因为交叉注意力已经被用于扩散模型。

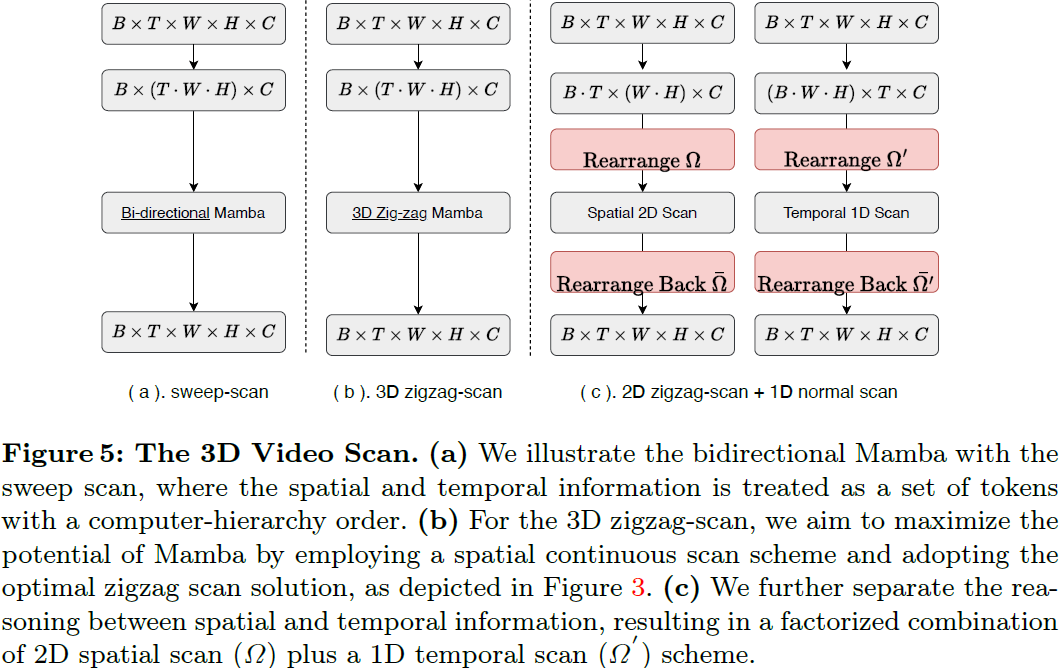
通过分解空间和时间信息泛化到 3D 视频。在前面的章节中，我们的重点是在空间 2D Mamba 上，我们设计了几种空间连续、空间填充的 2D 扫描方案。在本节中，我们旨在利用这一经验，帮助设计相应的 3D 视频处理机制。我们通过从传统的方向性 Mamba 推断开始我们的设计过程，如图 5 所示。给定一个视频特征输入 z ∈ R^(B×T×C×W×H)，我们提出了三个视频 Mamba 块的变体，以促进 3D 视频生成。

遍历扫描（Sweep-scan）：在这种方法中，我们直接将 3D 特征 z 展平，而不考虑空间或时间的连续性。值得注意的是，展平过程遵循计算机层次结构顺序，这意味着展平表示中没有保留连续性。
3D Zigzag：与之前小节中的 2D Zigzag 公式相比，我们遵循类似的设计来将其推广到 3D Zigzag，以同时保持 2D 和 3D 中的连续性。潜在地，该方案具有更高的复杂性。我们启发式地列出了 8 种方案。然而，我们经验性地发现，该方案将导致次优的优化。
分解的 3D Zigzag = 2D Zigzag + 1D Sweep：为了解决次优优化问题，我们提出将空间和时间相关性分解为单独的 Mamba 块。它们的应用顺序可以根据需要进行调整，例如，“sstt” 或“ststst”，其中 “s” 表示空间 Zigzag Mamba，“t” 表示时间 Zigzag Mamba。

计算分析。对于一个视觉序列 T ∈ R^(1×M×D)，全局自注意力和 k 方向 mamba 和我们的 zigzag mamba 的计算复杂度如下：

其中，自注意力相对于序列长度 M 呈二次复杂度，而 Mamba 呈线性复杂度（N 是一个固定参数，默认设置为 16）。在这里，k 表示单个 Mamba 块中的扫描方向数。因此，相对于自注意力，k-mamba 和 zigzag 具有线性复杂度。此外，我们的 zigzag 方法可以消除 k 系列（series），进一步降低总体复杂度。完成了改进的视觉归纳偏差集成 Zigzag Mamba 网络的设计后，我们继续将其与新的扩散框架结合，如下所示。

3.3 扩散框架：随机插值

（2021|ICLR，扩散先验，VE-SDE，逼真和忠实的权衡）SDEdit：使用随机微分方程引导图像合成和编辑

基于向量 v 和分数 s 进行抽样。根据 [3, 77]，xt 的时间相关概率分布 p_t(x) 也与逆时间 SDE [6] 的分布重合：

其中 ¯Wt 是逆时间维纳过程，wt > 0 是任意的时间相关扩散系数，s(x, t) = ∇log p_t(x) 是分数，v(x, t) 由条件期望给出

其中 αt 是 t 的递减函数，σt 是 t 的递增函数。这里，˙αt 和 ˙σt 分别表示 αt 和 σt 的时间导数。

只要我们能够估计速度 v(x, t) 和/或分数 s(x, t) 场，我们就可以将其用于采样过程，无论是通过概率流 ODE[73] 还是逆时间 SDE（7）。从 X_T = ε ∼ N(0, I) 开始求解逆向 SDE（7）可以生成来自近似数据分布 p_0(x) ∼ p(x) 的样本。在采样过程中，我们可以通过 ODE 或 SDE 直接采样，以在采样速度和准确度之间取得平衡。如果我们选择进行 ODE 采样，我们可以通过将噪声项 s 设置为零来实现这一点。

在 [3] 中，它显示了实践中需要估计两个量 sθ(x, t) 和 vθ(x, t) 中的一个。这直接来自约束

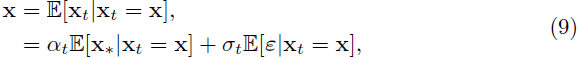
它可用于将分数 s(x, t) 重新表示为如下速度 v(x, t) 的等式：

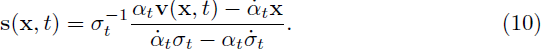
因此，速度 v(x, t) 和分数 s(x, t) 可以相互转换。我们将说明如何计算它们如下。

估计分数 s 和速度 v。在基于分数的扩散模型 [73] 中已经表明，分数可以使用损失函数

参数化地估计为 sθ(x, t)。类似地，速度 v(x, t) 可以通过以下损失函数参数化地估计为 vθ(x, t)：

其中，θ 代表我们在前面章节中描述的 Zigzag Mamba 网络，因为其简单性和相对地直线轨迹

我们采用线性路径进行训练。

我们注意到，任何时间相关的权重都可以包含在 (11) 和 (12) 中的积分中。当 T 变大时，这些权重因子在基于分数的模型中起着至关重要的作用。因此，它们提供了一个考虑到时间相关权重和随机性的一般形式。

4. 实验

7. 限制与未来工作

我们的方法仅依赖于具有 DiT 风格布局和调节方式的 Mamba 块。然而，我们工作的一个潜在限制是，我们无法穷尽地列出给定特定全局 patch 大小的所有可能的空间连续的之字扫描方案。目前，我们根据经验设置这些扫描方案，这可能导致次优的性能。此外，由于 GPU 资源的限制，我们无法探索更长的训练持续时间，尽管我们预计会得出类似的结论。

对于未来的工作，我们的目标是深入研究 Zigzag Mamba 的各种应用，利用其用于长序列建模的可扩展性。这种探索可能会导致在不同领域和应用程序中改进对 Mamba 框架的利用。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/559629