基于改进 PSO 算法的时间最优机械臂轨迹规划_机械臂轨迹优化

        以时间最优为目标，采用改进粒子群算法(PSO)对6自由度机械臂轨迹进行优化的方法。首先，在关节空间下利用机械臂正逆运动学原理获取其轨迹插值点;其次，为了使机械臂能够快速平稳地到达目标位置，采用3-5-3多项式对其轨迹进行插值;最后，使用改进PSO算法对分段多项式插值构造的轨迹进行优化，实现6自由度机械臂时间最优的轨迹规划。通过MATLAB仿真实验可以得到机械臂各个关节的加速度、速度和位置的轨迹信息。

1、机械臂的正运动学分析

puma560机器人DH参数表如下：

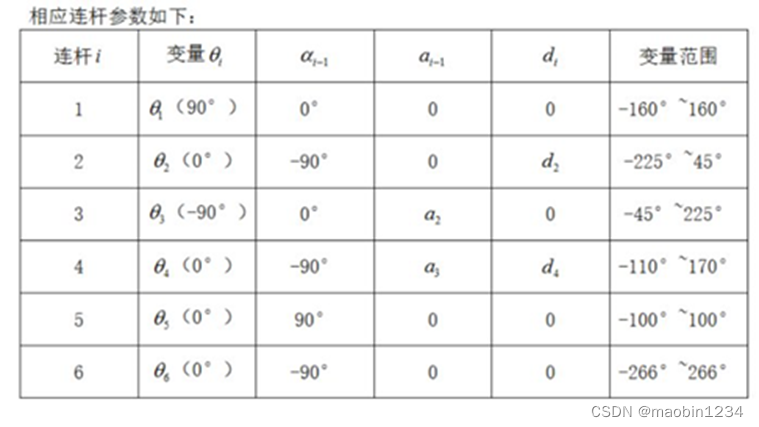
matlab建模如下：

% 轨迹规划中，首先建立机器人模型，6R机器人模型，名称modified puma560。
% 定义机器人 a--连杆长度，d--连杆偏移量
	a2=0.4318;a3=0.02032;d2=0.14909;d4=0.43307;
%			 thetai    di      ai-1        alphai-1
    L1 = Link([pi/2    0       0               0], 'modified');
    L2 = Link([0       d2      0           -pi/2], 'modified');
    L3 = Link([-pi/2   0       a2              0], 'modified');
    L4 = Link([0       d4      a3          -pi/2], 'modified');
    L5 = Link([0       0  	   0            pi/2], 'modified');
    L6 = Link([0       0       0           -pi/2], 'modified');
    robot = SerialLink([L1,L2,L3,L4,L5,L6]);
    robot.name = 'modified puma560';
%   robot.display();
%	robot.teach();

2、机械臂的轨迹规划方法

        采用3-5-3分段多项式对机械臂的运行轨迹进行插值，在一定的约束条件下，该多项式既可以保证各关节位置、速度和加速度的连续，也可以减小计算量和避免凸包性过差等问题。3-5-3分段多项式函数的表达式为：

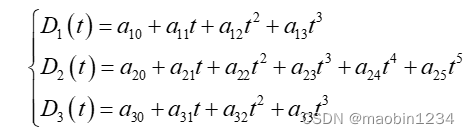
各段分别进行一阶求导和二阶求导之后，从而可获得三段运动轨迹曲线的速度与加速度函数为：

        机械臂各个关节通过起始点β1，路径点β2、β3和终止点β4时，β1和β4处的速度和加速度均为0，其他插值点重合处的速度和加速度应相等。

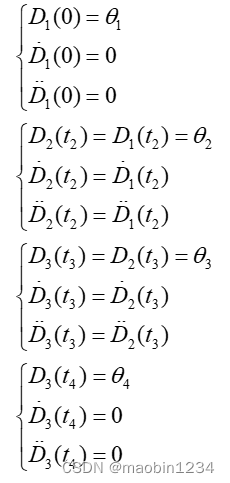
        因此利用上述的约束条件可以获取到一个非齐次线性方程组为：

        各个矩阵的表达式为：

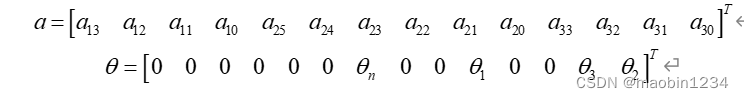
        由于已知各个路径点的位置和各段轨迹所需要的时间h，可以得到的系数矩阵为：

3、改进粒子群算法的轨迹优化

        以时间最少为目标，利用改进PSO算法对6自由度机械臂的运动轨迹进行规划，选取每个关节完成每段轨迹所用的时间t1，t2，t3构成一个三维的粒子群，其适应度函数表达式为:

F = t1 + t2 + t3

        PSO算法是一种模拟鸟群捕食活动的智能算法，它凭借着参数少、收敛迅速、结构简单和易控制等特点，在处理优化问题中更加快速便捷，但是传统的PSO算法容易受到待优化函数的影响提前收敛到局部最优。在每次迭代过程中，粒子群中的所有粒子都必须从当前的位置根据其更新的速度向新的位置移动。其粒子的速度和位置更新公式为：

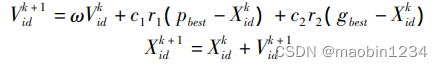
        标准粒子群算法中的参数是固定不变的。ω描述的是粒子的惯性，在进化前期ω应该更大一些，保证每个粒子能够独立飞行充分搜索空间，后期应该小一点，多向其他粒子学习。c1和c2分别描述的是个体和全局的最大飞行步长，前期c1尽可能的大一些，后期c2应尽可能的大一些，这样就可以平衡粒子的全局搜索能力和局部搜索能力。3个参数共同影响了粒子的飞行方向，假设其他粒子找到了更好的位置，但是当前粒子的惯性太大不能很快地飞向更优的位置，这就有可能导致算法易早熟或者是算法后期收敛缓慢等问题。针对PSO易早熟且后期收敛速度慢等问题，对粒子群算法进行以下几点改进:

        1、采用混沌序列初始化代替PSO中的随机初始化粒子的种群。PSO中随机初始化易导致种群初始化分布不均从而影响算法的优化。混沌序列初始化种群时具有遍历性、随机性和均匀性的特点，是在规定的范围内根据本身规律不重叠地遍历整个搜索空间。因此，混沌序列初始化的种群可以有效地提高PSO算法。本文采用Logistic混沌映射，其表达形式：

x(i)=4.*x(i-1).*(1-x(i-1))

        2、自适应调整惯性权重的方法。常用的线性递减的惯性权重对POS跳出局部最优有一定作用，但是无论粒子的适应度是否变得更好，惯性权重都会根据迭代次数以线性速度递减。所以依靠线性递减惯性因子的粒子群算法有时也会陷入局部最优。自适应调整惯性权重综合考虑了粒子的迭代次数和粒子的目标值，初期使用较大的ω增强粒子的全局搜索能力，当有粒子飞行至最优点附近时，则减小ω增加粒子的局部搜索能力，这样对PSO优化的结果有较大提升。自适应调整惯性权重的表达式为：

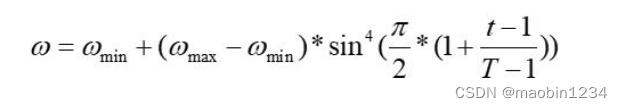
        3、将局部和全局的学习因子c1和c2联合起来。当增大c1时，会增强粒子的个体认知能力，但是收敛速度缓慢;当增大c2时，会增强粒子的社会认知能力，收敛速度迅速，但是极易使算法早熟。为了保证PSO算法的搜索能力和协调粒子的个体认知和社会认知能力，采用动态调整学习因子的方法，将学习因子的取值与粒子当前的迭代次数联系起来。在搜索初期粒子个体的搜索意义大于全局的搜索意义，所以c1＞c2;在搜索后期为了更加快速地获得全局最优解，应增加粒子与种群之间的交流，所以c1＜c2。其函数表达式为:

        改进 PSO 算法对 6 自由度机械臂轨迹优化的具 体步骤如下:

        步骤1:机械臂每个关节3段轨迹的运动时间(t1、t2、t3)构成一个三维的搜索空间，采用混沌初始化产生N个粒子(共有3N个粒子)构成种群，并初始化种群中各粒子的位置和速度。
        步骤2:将初始化产生的N个三维时间组合带入式，求得各分段函数的系数。
        步骤3:判断机械臂各关节3段运动轨迹的速度和加速度是否满足最大约束条件，若3段都满足约束条件，则将3段轨迹的运行时间带入计算其适应度值，若3段中任意1段的速度或加速度不满足约束，则赋予一个很大的值作为该粒子的适应度值，以便在下一次迭代中淘汰该粒子。
        步骤4:经过k次迭代后，通过比较个体极值和全局极值的适应度值，选出适应度最佳的粒子，即为最优极值。
        步骤5:当机械臂所有关节的轨迹都完成优化时，每段时间取各关节完成该段轨迹所需要的最长时间，进而确保机械臂的所有关节都能完成轨迹的运行。

        根据各个点的位置信息和约束条件可以得到相应的时间

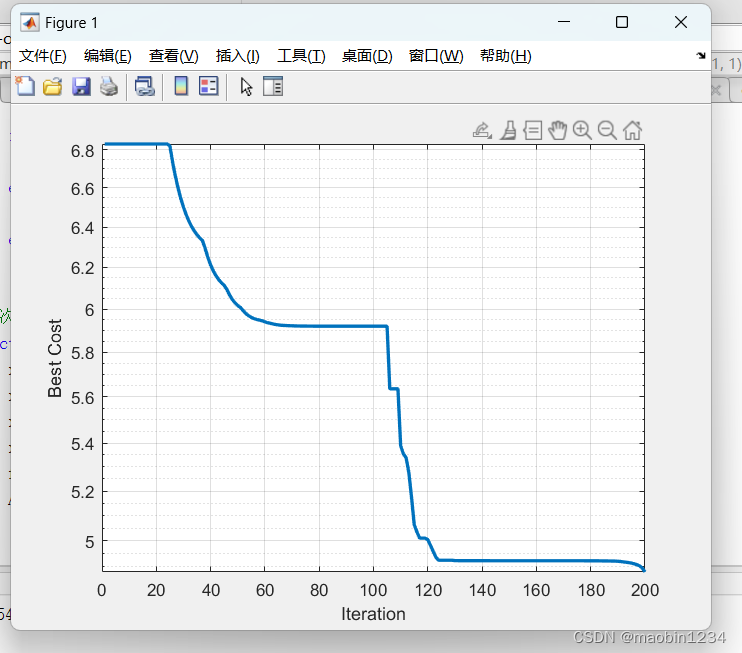
        由于各个关键点是在笛卡尔空间指定，需要使各关节的角度最终到达终止点。当某个关节提前到达关键点位置时，其他关节之后到达，为了使机械臂到达终止点，先到达关键点位置的关节会停止运动，待其他的关节到达之后再一起运动，这样会造成额外能量的损耗。因此使各个关节同步运动，即取各关节完成每段轨迹时间的最大值，既可以实现优化目的，也可以减少能量的消耗。

        取得最大时间后可以带入得到：

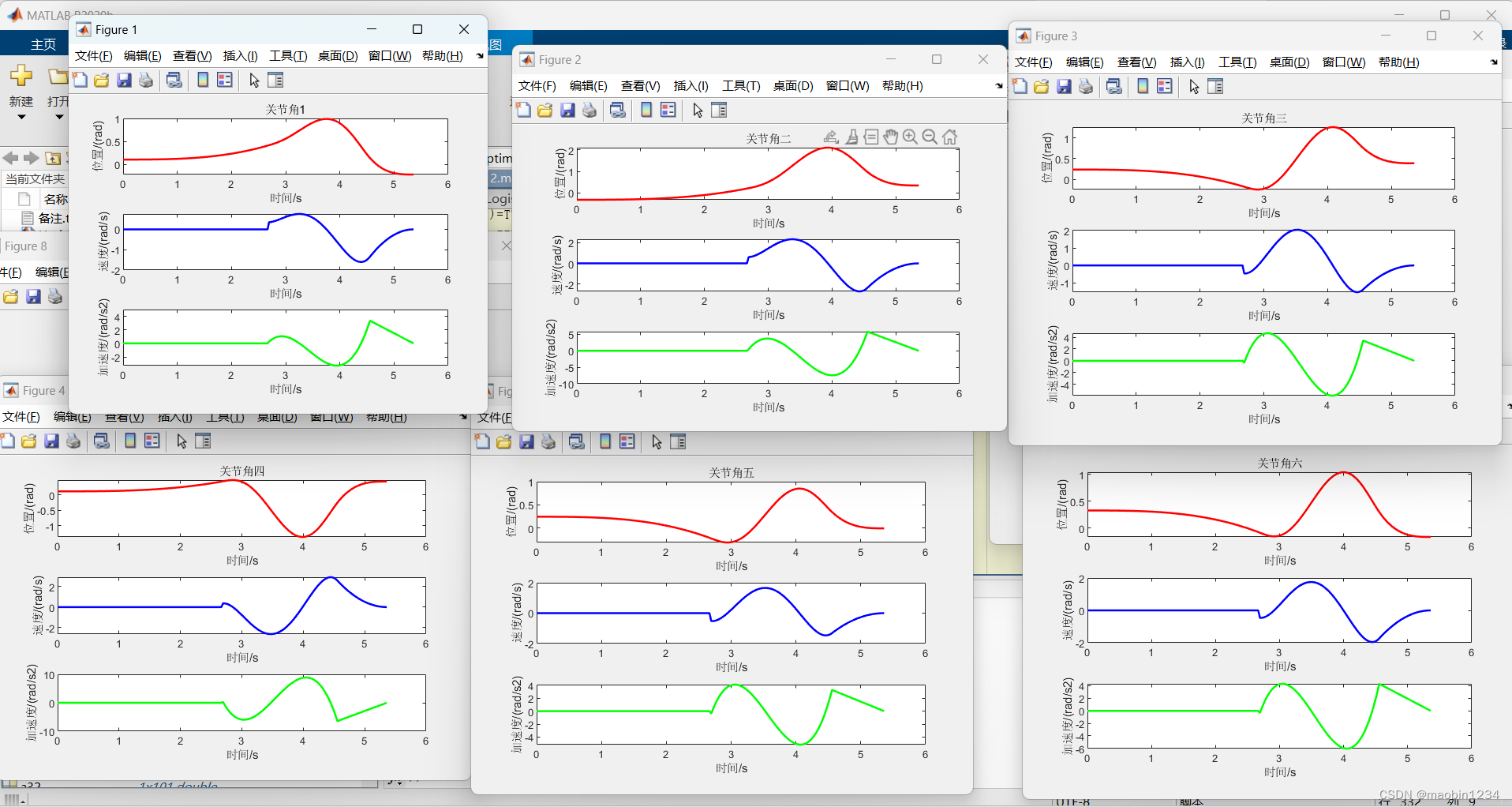
将各个关节的位置信息带入可以得到：

4.Matlab代码

https://mbd.pub/o/bread/ZJ6Vm5Zq