笔触狂放9

这个屌丝很懒，什么也没留下！

热门标签

循环神经网络RNN_rnn unfold

作者：笔触狂放9 | 2024-05-16 15:23:43

踩

rnn unfold

Gated Recurrent Unit (GRU)

Peephole LSTM

Bi-directional RNN(双向RNN)

Continuous time RNN(CTRNN)

在前面的task学习了全连接神经网络和卷积神经网络，以及它们的训练和使用。他们都只能单独的取处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。比如，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。这时，就需要用到深度学习领域中另一类非常重要神经网络：循环神经网络(Recurrent Neural Network)。

循环神经网络基本原理

循环神经网络是一种人工神经网络，它的节点间的连接形成一个遵循时间序列的有向图，它的核心思想是，样本间存在顺序关系，每个样本和它之前的样本存在关联。通过神经网络在时序上的展开，我们能够找到样本之间的序列相关性。

文本：字母和词汇的序列
语音：音节的序列
视频：图像帧的序列
时态数据：气象观测数据，股票交易数据、房价数据等

RNN的一般结构

6.10

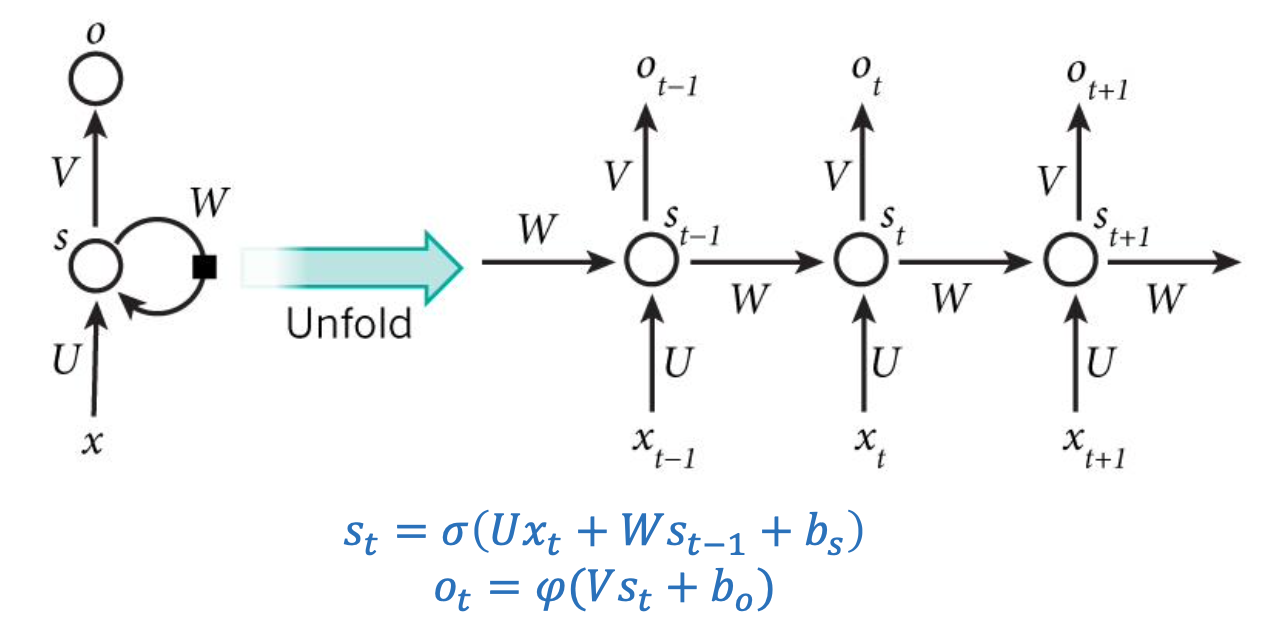
其中各个符号的表示： $x_t,s_t,o_t$ 分别表示的是tt时刻的输入、记忆和输出， $U,V,W$ 是RNN的连接权重， $b_s,b_o$ 是RNN的偏置， $\sigma,\varphi$ 是激活函数， $\sigma$ 通常选tanh或sigmoid， $\varphi$ 通常选用softmax。

我们现在这样来理解，如果把上面有 $W$ 的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。 $x$ 是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）； $s$ 是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，这一层其实是多个节点，节点数与向量 $s$ 的维度相同）；

$U$ 是输入层到隐藏层的权重矩阵， $o$ 也是一个向量，它表示输出层的值； $V$ 是隐藏层到输出层的权重矩阵。

那么，现在我们来看看 $W$ 是什么。循环神经网络的隐藏层的值 $s$ 不仅仅取决于当前这次的输入 $x$ ，还取决于上一次隐藏层的值 $s$ 。权重矩阵 $W$ 就是隐藏层上一次的值作为这一次的输入的权重。

图右unfold是RNN按照时间线的展开，这个网络在ｔ时刻接收到输入 $x_t$ 之后，隐藏层的值是 $s_t$ ，输出值是 $o_t$ 。关键一点是， $s_t$ 的值不仅仅取决于 $x_t$ ，还取决于 $s_{t-1}$ 。我们可以用下面的公式来表示循环神经网络的计算方法：

$\begin{align*} &s_t=\sigma(Ux_t+Ws_{t-1}+b_s) \\ & o_t=\varphi(Vs_t+b_o) \end{align*}$

其中 softmax 函数，用于分类问题的概率计算。本质上是将一个K维的任意实数向量压缩 (映射)成另一个K维的实数向量，其中向量中的每个元素取值都介于(0，1)之间。

$\sigma(\vec{z})_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{K} e^{z_{j}}}$

RNN训练算法 - BPTT

我们先来回顾一下BP算法，就是定义损失函数 Loss 来表示输出 $\hat{y}$ 和真实标签 $y$ 的误差，通过链式法则自顶向下求得 Loss 对网络权重的偏导。沿梯度的反方向更新权重的值，直到 Loss 收敛。而这里的 BPTT 算法就是加上了时序演化，后面的两个字母 TT 就是 Through Time。

6.17

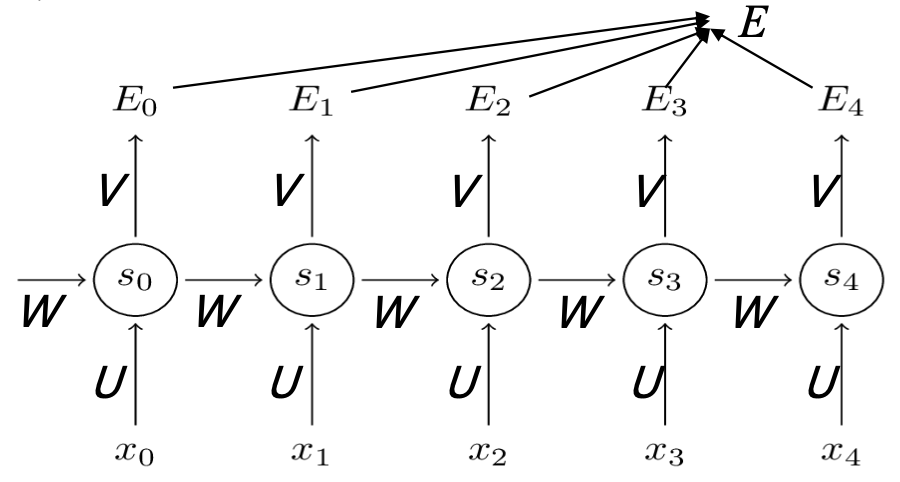
我们先定义输出函数：

$\begin{array}{l}s_{t}=\tanh \left(U x_{t}+W s_{t-1}\right) \\ \hat{y}_{t}=\operatorname{softmax}\left(V s_{t}\right)\end{array}$

再定义损失函数：

$\begin{aligned} E_{t}\left(y_{t}, \hat{y}_{t}\right) =-y_{t} \log \hat{y}_{t} \\ E(y, \hat{y}) =\sum_{t} E_{t}\left(y_{t}, \hat{y}_{t}\right) \\ =-\sum_{t} y_{t} \log \hat{y}_{t}\end{aligned}$

6.18

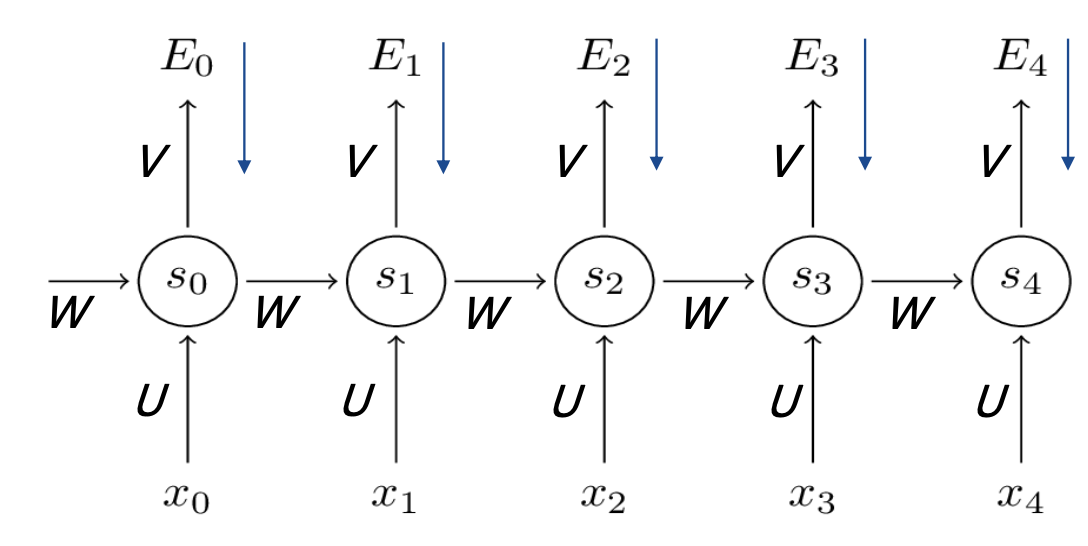
以下为复合函数的链式求导过程

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

前向计算每个神经元的输出值；
反向计算每个神经元的误差项值，它是误差函数E对神经元j的加权输入的偏导数；
计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。

RNN的代码实现

完整代码参考GitHub:learn_dl/rnn.py at master · hanbt/learn_dl · GitHub


import numpy as np
from cnn import element_wise_op
from activators import ReluActivator, IdentityActivator
 
'''我们用RecurrentLayer类来实现一个循环层。下面的代码是初始化一个循环层，可以在构造函数中设置卷积层的超参数。我们注意到，循环层有两个权重数组，U和W
'''
class RecurrentLayer(object):
    def __init__(self, input_width, state_width,
                 activator, learning_rate):
        self.input_width = input_width
        self.state_width = state_width
        self.activator = activator
        self.learning_rate = learning_rate
        self.times = 0       # 当前时刻初始化为t0
        self.state_list = [] # 保存各个时刻的state
        self.state_list.append(np.zeros(
            (state_width, 1)))           # 初始化s0
        self.U = np.random.uniform(-1e-4, 1e-4,
            (state_width, input_width))  # 初始化U
        self.W = np.random.uniform(-1e-4, 1e-4,
            (state_width, state_width))  # 初始化W
 
'''在forward方法中，实现循环层的前向计算，这部分比较简单。'''
    def forward(self, input_array):
        '''
        根据『式2』进行前向计算
        '''
        self.times += 1
        state = (np.dot(self.U, input_array) +
                 np.dot(self.W, self.state_list[-1]))
        element_wise_op(state, self.activator.forward)
        self.state_list.append(state)
 
'''在backword方法中，实现BPTT算法。'''
    def backward(self, sensitivity_array, 
                 activator):
        '''
        实现BPTT算法
        '''
        self.calc_delta(sensitivity_array, activator)
        self.calc_gradient()
 
'''在update方法中，实现梯度下降算法'''
    def update(self):
        '''
        按照梯度下降，更新权重
        '''
        self.W -= self.learning_rate * self.gradient
 
    def calc_delta(self, sensitivity_array, activator):
        self.delta_list = []  # 用来保存各个时刻的误差项
        for i in range(self.times):
            self.delta_list.append(np.zeros(
                (self.state_width, 1)))
        self.delta_list.append(sensitivity_array)
        # 迭代计算每个时刻的误差项
        for k in range(self.times - 1, 0, -1):
            self.calc_delta_k(k, activator)
 
    def calc_delta_k(self, k, activator):
        '''
        根据k+1时刻的delta计算k时刻的delta
        '''
        state = self.state_list[k+1].copy()
        element_wise_op(self.state_list[k+1],
                    activator.backward)
        self.delta_list[k] = np.dot(
            np.dot(self.delta_list[k+1].T, self.W),
            np.diag(state[:,0])).T
 
    def calc_gradient(self):
        self.gradient_list = [] # 保存各个时刻的权重梯度
        for t in range(self.times + 1):
            self.gradient_list.append(np.zeros(
                (self.state_width, self.state_width)))
        for t in range(self.times, 0, -1):
            self.calc_gradient_t(t)
        # 实际的梯度是各个时刻梯度之和
        self.gradient = reduce(
            lambda a, b: a + b, self.gradient_list,
            self.gradient_list[0]) # [0]被初始化为0且没有被修改过
 
    def calc_gradient_t(self, t):
        '''
        计算每个时刻t权重的梯度
        '''
        gradient = np.dot(self.delta_list[t],
            self.state_list[t-1].T)
        self.gradient_list[t] = gradient
 
'''循环层是一个带状态的层，每次forword都会改变循环层的内部状态，这给梯度检查带来了麻烦。因此，我们需要一个reset_state方法，来重置循环层的内部状态'''
    def reset_state(self):
        self.times = 0       # 当前时刻初始化为t0
        self.state_list = [] # 保存各个时刻的state
        self.state_list.append(np.zeros(
            (self.state_width, 1)))      # 初始化s0
 
 
def data_set():
    x = [np.array([[1], [2], [3]]),
         np.array([[2], [3], [4]])]
    d = np.array([[1], [2]])
    return x, d
 
'''最后，是梯度检查的代码'''
def gradient_check():
    '''
    梯度检查
    '''
    # 设计一个误差函数，取所有节点输出项之和
    error_function = lambda o: o.sum()
    
    rl = RecurrentLayer(3, 2, IdentityActivator(), 1e-3)
 
    # 计算forward值
    x, d = data_set()
    rl.forward(x[0])
    rl.forward(x[1])
    
    # 求取sensitivity map
    sensitivity_array = np.ones(rl.state_list[-1].shape,
                                dtype=np.float64)
    # 计算梯度
    rl.backward(sensitivity_array, IdentityActivator())
    
    # 检查梯度
    epsilon = 10e-4
    for i in range(rl.W.shape[0]):
        for j in range(rl.W.shape[1]):
            rl.W[i,j] += epsilon
            rl.reset_state()
            rl.forward(x[0])
            rl.forward(x[1])
            err1 = error_function(rl.state_list[-1])
            rl.W[i,j] -= 2*epsilon
            rl.reset_state()
            rl.forward(x[0])
            rl.forward(x[1])
            err2 = error_function(rl.state_list[-1])
            expect_grad = (err1 - err2) / (2 * epsilon)
            rl.W[i,j] += epsilon
            print 'weights(%d,%d): expected - actural %f - %f' % (
                i, j, expect_grad, rl.gradient[i,j])
 
 
def test():
    l = RecurrentLayer(3, 2, ReluActivator(), 1e-3)
    x, d = data_set()
    l.forward(x[0])
    l.forward(x[1])
    l.backward(d, ReluActivator())
    return l

实践中经典的RNN

RNN的梯度爆炸和消失问题

实践中前面介绍的RNN并不能很好的处理较长的序列。一个主要的原因是，RNN在训练中很容易发生梯度爆炸和梯度消失，这导致训练时梯度不能在较长序列中一直传递下去，从而使RNN无法捕捉到长距离的影响。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会收到NaN错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域
使用relu代替sigmoid和tanh作为激活函数
使用其他结构的RNNs，比如长短时记忆网络（LTSM）和Gated Recurrent Unit（GRU），这是最流行的做法

LSTM

LSTM，即长短时记忆网络，于1997年被Sepp Hochreiter 和Jürgen Schmidhuber提出来，LSTM是一种用于深度学习领域的人工循环神经网络（RNN）结构。一个LSTM单元由输入门、输出门和遗忘门组成，三个门控制信息进出单元。

6.20

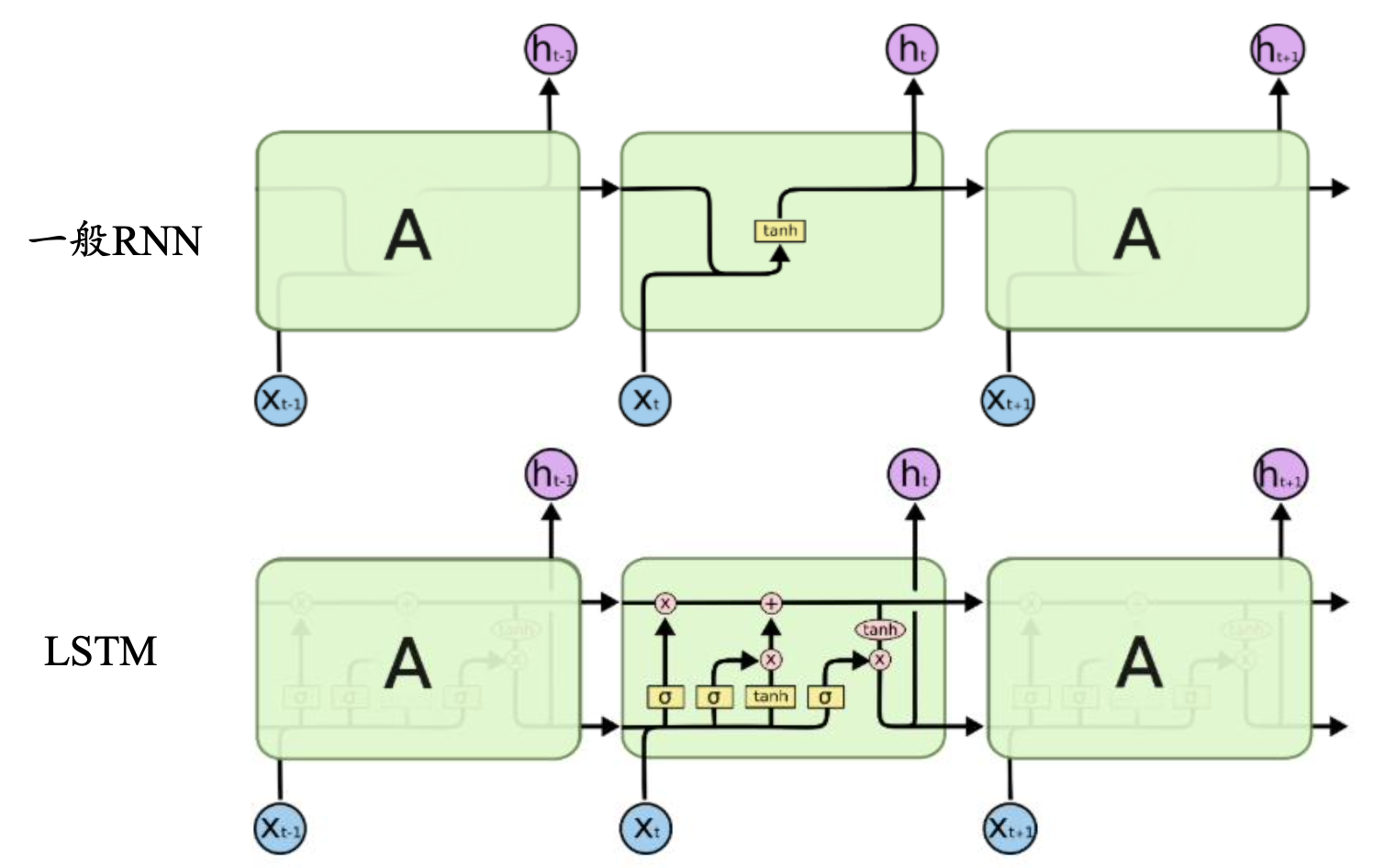
LSTM依靠贯穿隐藏层的细胞状态实现隐藏单元之间的信息传递，其中只有少量的线性操作
LSTM引入了“门”机制对细胞状态信息进行添加或删除，由此实现长程记忆
“门”机制由一个Sigmoid激活函数层和一个向量点乘操作组成，Sigmoid层的输出控制了信息传递的比例

Gated Recurrent Unit (GRU)

Gated Recurrent Unit (GRU)，是在2014年提出的，可认为是LSTM 的变种，它的细胞状态与隐状态合并，在计算当前时刻新信息的方法和LSTM有所不同；GRU只包含重置门和更新门；在音乐建模与语音信号建模领域与LSTM具有相似的性能，但是参数更少，只有两个门控。

6.19

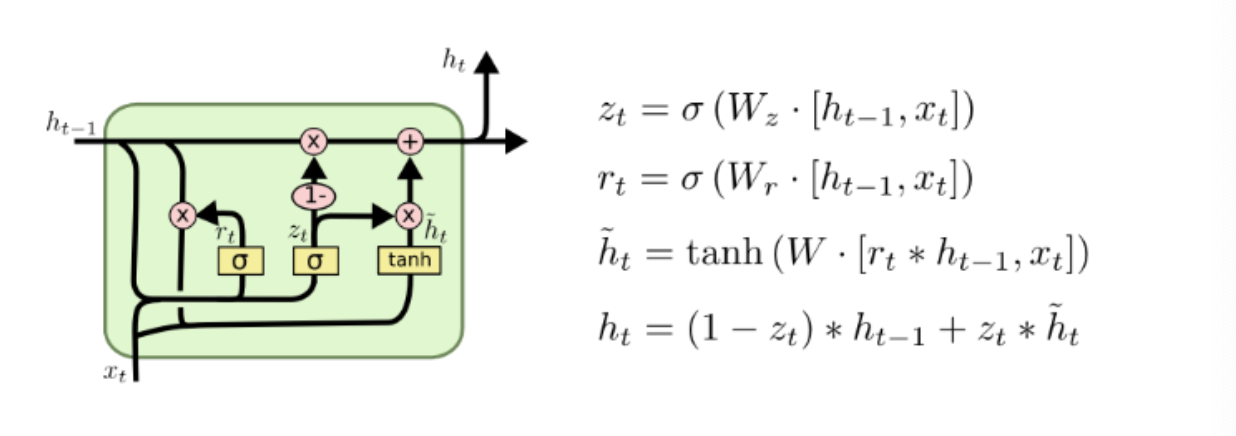
Peephole LSTM

让门层也接受细胞状态的输入，同时考虑隐层信息的输入。

6.25

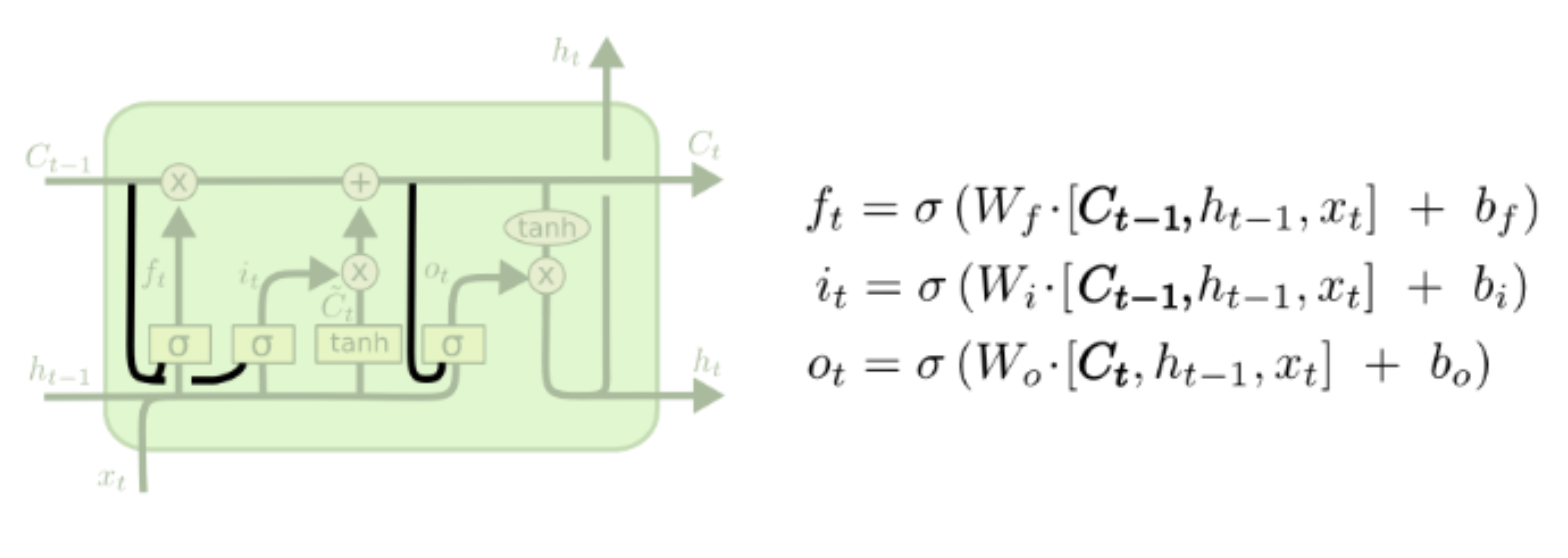
Bi-directional RNN(双向RNN)

Bi-directional RNN(双向RNN)假设当前t的输出不仅仅和之前的序列有关，并且还与之后的序列有关，例如：完形填空，它由两个RNNs上下叠加在一起组成，输出由这两个RNNs的隐藏层的状态决定。

6.26

6.27

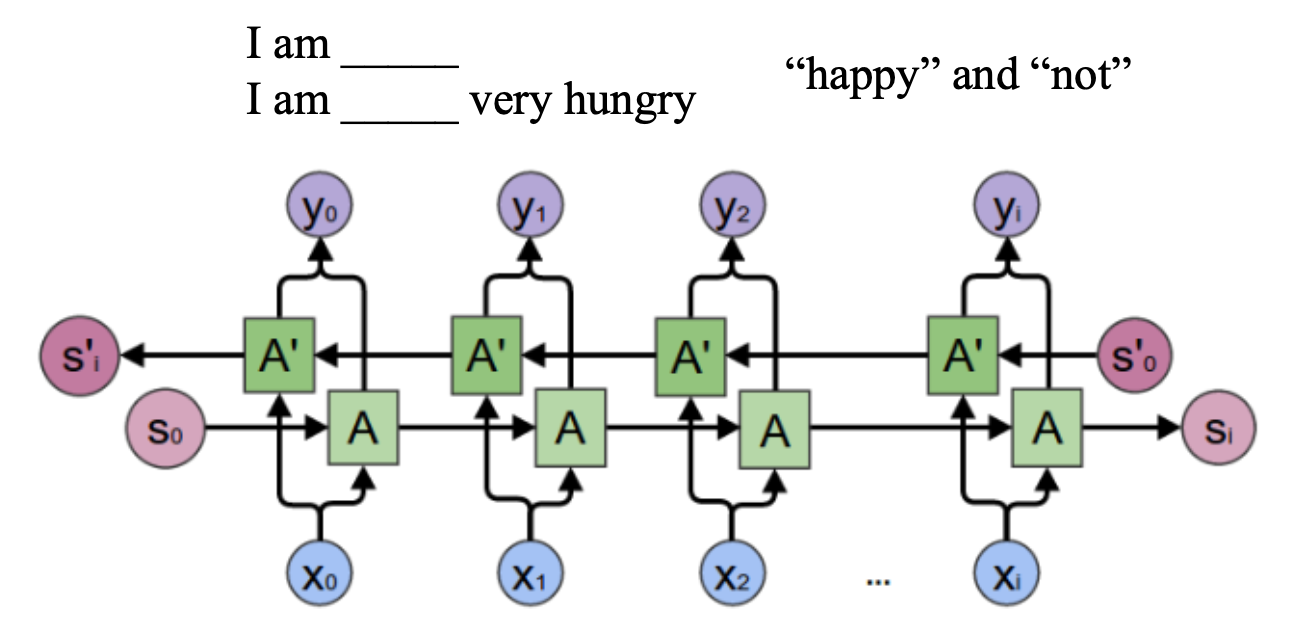
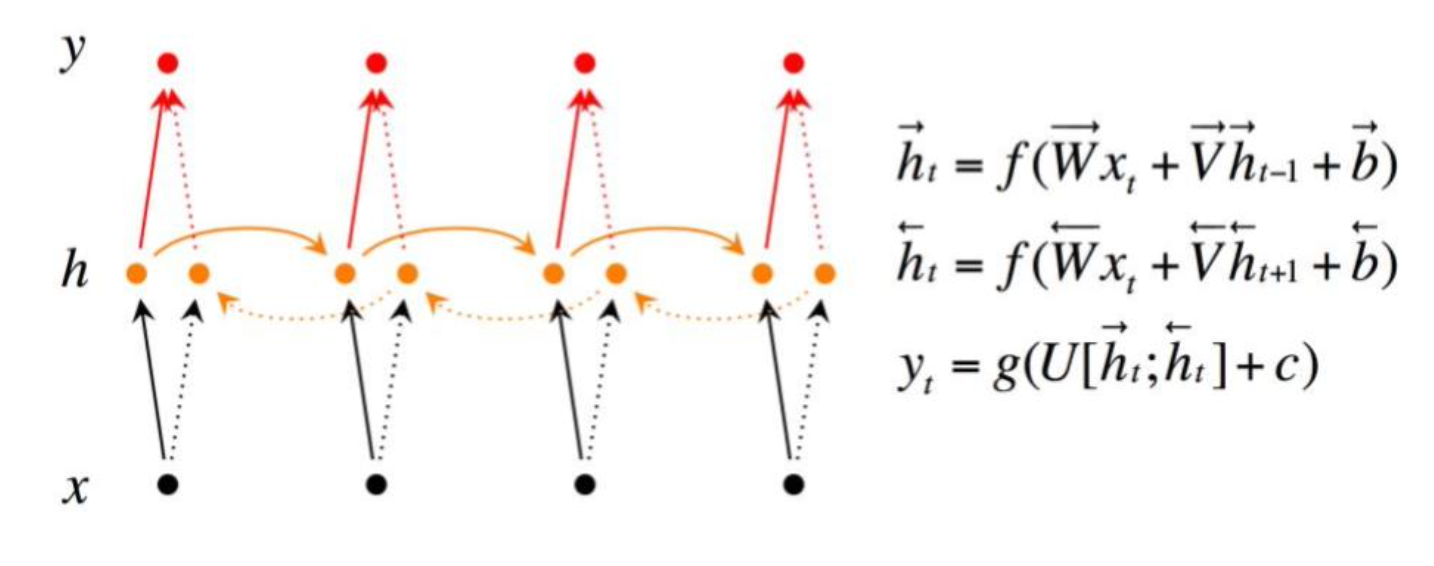
Continuous time RNN(CTRNN)

CTRNN利用常微分方程系统对输入脉冲序列神经元的影响进行建模。CTRNN被应用到进化机器人中，用于解决视觉、协作和最小认知行为等问题。

6.28

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/579411