链表 (2)

---

正文开始

一 . 前言

补充说明：
1、链式机构在逻辑上是连续的，在物理结构上不⼀定连续
2、节点⼀般是从堆上申请的
3、从堆上申请来的空间，是按照⼀定策略分配出来的，每次申请的空间可能连续，可能不连续

本篇旨在实现链表的剩下的方法

//查找 
SLTNode* SLTFind(SLTNode* phead, SLTDataType x);
//在指定位置之前插⼊数据 
void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);
//删除pos节点 
void SLTErase(SLTNode** pphead, SLTNode* pos);
//在指定位置之后插⼊数据 
void SLTInsertAfter(SLTNode* pos, SLTDataType x);
//删除pos之后的节点 
void SLTEraseAfter(SLTNode* pos);
//销毁链表 
void SListDesTroy(SLTNode** pphead);

1
2
3
4
5
6
7
8
9
10
11
12
13

---

二 . 头文件声明

接上文, 在头文件中先声明以下函数, 然后在.c文件中进行实现
见3实现详情

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int DataType;

typedef struct SListNode
{
	DataType data;
	struct SListNode* next;
}SLTNode;

void SLTPrint(SLTNode* phead);

//尾插
void SLTPushBack(SLTNode** pphead, DataType x);
//头插
void SLTPushFront(SLTNode** pphead, DataType x);
//尾删
void SLTPopBack(SLTNode** pphead);
//头删
void SLTPopFront(SLTNode** pphead);

//查找
SLTNode* SLTFind(SLTNode* phead, DataType x);

//在指定位置之前插入数
void SLTInsert(SLTNode** pphead, SLTNode* pos, DataType x);
//在指定位置之后插入数据
void SLTInsertAfter(SLTNode* pos, DataType x);

//删除指定位置结点
void SLTErase(SLTNode** pphead, SLTNode* pos);
//删除指定位置之后的结点
void SLTEraseAfter(SLTNode* pos);

//销毁链表
void SLTDestory(SLTNode** pphead);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

---

三 . 代码思绪

1. 查找函数的实现

查找不需要改变头结点所指向的地址, 所以不需要取地址, 直接接收形参和要查找的数据, 临时变量pcur用来遍历链表, 让发现所要查找的数据与之遍历的结点所匹配时, 停止遍历返回此节点, 没有找到返回空.

SLTNode* SLTFind(SLTNode* phead, DataType x)
{
	SLTNode* pcur = phead;
	while (pcur)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2. 在指定位置之前插入

需要断言头结点和指定位置都不能为NULL, 调用函数创建新的结点, 首先需要先找到指定位置的前一个结点, 找到之后, 先让新节点的指针域指向pos结点, 然后再让前一个结点的指针域指向新节点.
但是这里需要注意, 如果pos为头结点, 则prev会对NULL进行解引用, 程序报错, 所以需要单独判断, 让pos为头结点时可以使用头插, 也可以先让新节点的下一个位置指向头结点, 然后再改变头指针指向新节点.

注: 创建新节点的函数在上篇

void SLTInsert(SLTNode** pphead, SLTNode* pos, DataType x)
{
	assert(pphead && *pphead);
	assert(pos);
	
	SLTNode* newnode = SLTBuyNode(x);

	if (pos == *pphead)
	{
		newnode->next = *pphead;
		*pphead = newnode;
		//SLTPushFront(pphead,x);
	}
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		newnode->next = pos;
		prev->next = newnode;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

测试一下:

	SLTNode* plist = NULL;
	SLTPushBack(&plist, 100);
	SLTPrint(plist);
	SLTPushBack(&plist, 88);
	SLTPrint(plist);

	SLTPushFront(&plist,99);
	SLTPrint(plist);

	SLTPopBack(&plist);
	SLTPrint(plist);

	SLTPopFront(&plist);
	SLTPrint(plist);

	SLTNode* find =  SLTFind(plist, 100);
	SLTPrint(find);

	SLTInsert(&plist,find,200);
	SLTPrint(plist);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

执行结果:

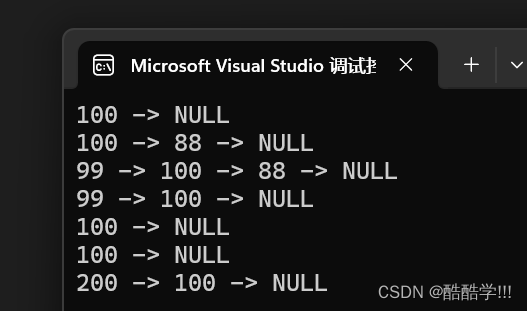
只能说:

打印代码在这里:

void SLTPrint(SLTNode* phead)
{
	SLTNode* pcur = phead;
	while (pcur)
	{
		printf("%d -> ", pcur->data);
		pcur = pcur->next;
	}
	printf("NULL\n");
}
1
2
3
4
5
6
7
8
9
10

3. 在指定位置之后插入

不需要传递头指针了, 因为用不到, 可以直接通过pos->next找到要插入的位置, 断言pos不能为NULL, 创建新结点, 先让新节点的指针域指向pos的下一个结点, 之后让pos的指针域指向新的结点.

void SLTInsertAfter(SLTNode* pos, DataType x)
{
	assert(pos);
	SLTNode* newnode = SLTBuyNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}
1
2
3
4
5
6
7

测试一下:

	SLTNode* plist = NULL;
	SLTPushBack(&plist, 100);
	SLTPrint(plist);
	SLTPushBack(&plist, 88);
	SLTPrint(plist);

	SLTPushFront(&plist,99);
	SLTPrint(plist);

	SLTPopBack(&plist);
	SLTPrint(plist);

	SLTPopFront(&plist);
	SLTPrint(plist);

	SLTNode* find =  SLTFind(plist, 100);
	SLTPrint(find);

	SLTInsert(&plist,find,200);
	SLTPrint(plist);

	SLTInsertAfter(find,300);
	SLTPrint(plist);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

代码结果:

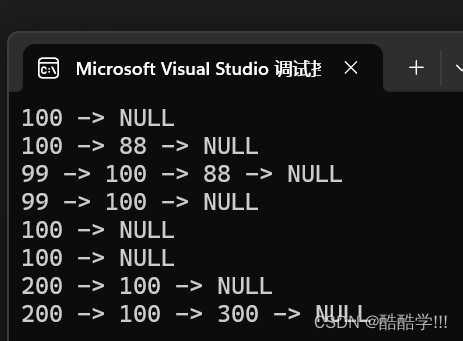
没毛病!

4. 删除指定位置的结点

首先还是需要断言, 不可以为空链表空地址, 不然你让我删什么, 先找到要删除位置的前一个结点, 因为要把它的指针域置为NULL, 否则删除pos节点后 它会成为野指针,定义prev, 找到前一个结点之后,让prev指向pos之后的那个结点, 跳过pos结点, 然后将pos结点释放掉,并且置为NULL.
注意如果要删除头指针的话这里遍历prev->next一样会非法访问NULL,所以需要单独判断, 直接调用头删方法即可, 思路是一样的.

void SLTErase(SLTNode** pphead, SLTNode* pos)
{
	assert(pos);
	assert(pphead && *pphead);

	if (pos == *pphead)
	{
		SLTPopFront(pphead);
	}
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		prev->next = pos->next;
		free(pos);
		pos = NULL;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

测试一下:

	SLTErase(&plist, find);
	SLTPrint(plist);
1
2

代码结果:
此时100已被删除

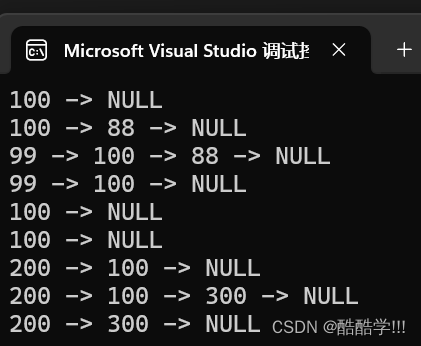
没毛病!

5. 删除指定位置之后的结点

这里也不需要传递头结点, 因为用不到, 需要断言pos和要删除的结点是否存在, 定义del记录一下要删除的结点, 之后直接让pos的指针域指向下下一个结点, 而此时要删除的结点已经保存在del中, 所以直接free掉,最后置为NULL.

void SLTEraseAfter(SLTNode* pos)
{
	assert(pos && pos->next);
	SLTNode* del = pos->next;
	pos->next = del->next;
	free(del);
	del = NULL;
}
1
2
3
4
5
6
7
8

测试一下:

	SLTEraseAfter(find);
	SLTPrint(plist);
1
2
3

代码运行结果:

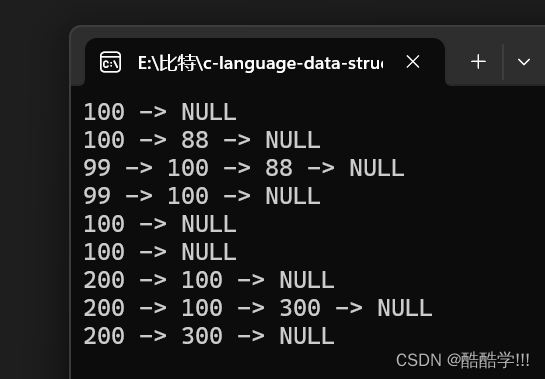
只能说:

6. 销毁链表

为空的话就需要销毁了, 所以先断言一下是否为NULL, 然后定义临时变量遍历链表, 存储好下一个待遍历的位置之后free掉pcur即可, 最后不要忘了将头指针也置为空

void SLTDestory(SLTNode** pphead)
{
	assert(pphead && *pphead);
	SLTNode* pcur = *pphead;
	while (pcur)
	{
		SLTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12

---

四 . 完整代码

SLTNode* SLTFind(SLTNode* phead, DataType x)
{
	SLTNode* pcur = phead;
	while (pcur)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	return NULL;
}

void SLTInsert(SLTNode** pphead, SLTNode* pos, DataType x)
{
	assert(pphead && *pphead);
	assert(pos);
	
	SLTNode* newnode = SLTBuyNode(x);

	if (pos == *pphead)
	{
		newnode->next = *pphead;
		*pphead = newnode;
		//SLTPushFront(pphead,x);
	}
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		newnode->next = pos;
		prev->next = newnode;
	}
}

void SLTInsertAfter(SLTNode* pos, DataType x)
{
	assert(pos);
	SLTNode* newnode = SLTBuyNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}

void SLTErase(SLTNode** pphead, SLTNode* pos)
{
	assert(pos);
	assert(pphead && *pphead);

	if (pos == *pphead)
	{
		SLTPopFront(pphead);
	}
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		prev->next = pos->next;
		free(pos);
		pos = NULL;
	}
}

void SLTEraseAfter(SLTNode* pos)
{
	assert(pos && pos->next);
	SLTNode* del = pos->next;
	pos->next = del->next;
	free(del);
	del = NULL;
}

void SLTDestory(SLTNode** pphead)
{
	assert(pphead && *pphead);
	SLTNode* pcur = *pphead;
	while (pcur)
	{
		SLTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

五 . 总结

链表是一种常见的数据结构，它由一系列节点组成，每个节点包含一个数据元素和一个指向下一个节点的指针。链表的优点是插入和删除操作的时间复杂度为O(1)，而不受链表长度的影响。然而，链表的缺点是访问元素的时间复杂度为O(n)，因为需要遍历整个链表。

链表常见的类型有单链表、双向链表和循环链表。

• 单链表：每个节点只有一个指向下一个节点的指针。
• 双向链表：每个节点既有指向下一个节点的指针，也有指向上一个节点的指针。
• 循环链表：链表中最后一个节点的指针指向链表中的第一个节点。

链表的操作包括插入、删除和查找。

• 插入操作：将一个新的节点插入到链表的某个位置，需要修改前后节点的指针。
• 删除操作：删除链表中的某个节点，需要修改前后节点的指针。
• 查找操作：根据给定的值查找链表中的节点。

在实际应用中，链表常用于实现栈、队列和图等数据结构。此外，链表还有一种特殊的应用——LRU缓存淘汰算法，用于解决缓存容量有限的情况下，如何选择合适的缓存进行淘汰的问题。

总结来说，链表是一种重要的数据结构，具有插入和删除操作效率高的优点，适用于需要频繁插入和删除操作的场景。但是在访问元素方面比较慢，需要遍历整个链表。了解链表的特点和操作有助于程序员更好地理解和应用链表。

---

完, 本文分享就到这里, 感谢大家的支持 关注 点赞 收藏 !!!