协同过滤算法是一个经典的推荐算法。它的基本思想是通过对用户历史行为数据的挖掘来发现用户的喜好偏向，基于不同的喜好偏向对用户进行划分并向用户推荐其可能喜好的产品。举个简单的例子，当我们出去买饮品的时候，我们通常会询问身边的朋友有没有推荐的，而我们一般更倾向于同我们口味类似的朋友那里得到推荐。这就是协同过滤的核心思想。

协同过滤算法分为两类，分别是

基于物品的协同过滤算法：给用户推荐与他之前喜欢的物品类似的物品

基于用户的协同过滤算法：给用户推荐与他兴趣相似的其他用户喜欢的物品

二、基于用户的协同过滤算法

人以群分：找到与该用户具有相似兴趣其他用户，将他们喜欢的但是该用户未曾见过的物品推荐给该用户。

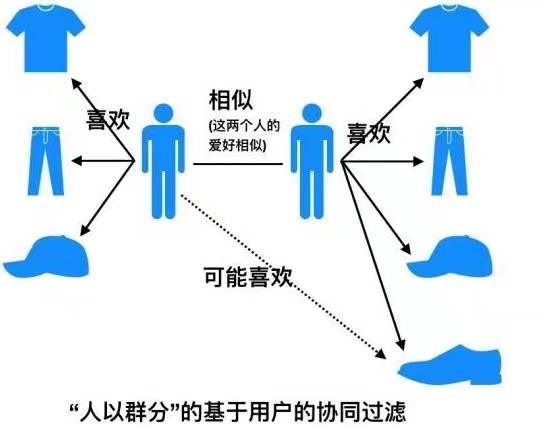
基于用户的协同过滤算法主要分为两个步骤：

（1）找到与用户A具有相似兴趣爱好的用户B，即计算用户之间的相似度；

（2）将用户B喜欢的但是用户A未曾见过的物品推荐给用户A。

2.1 实例

下面给大家举个例子具体看一下

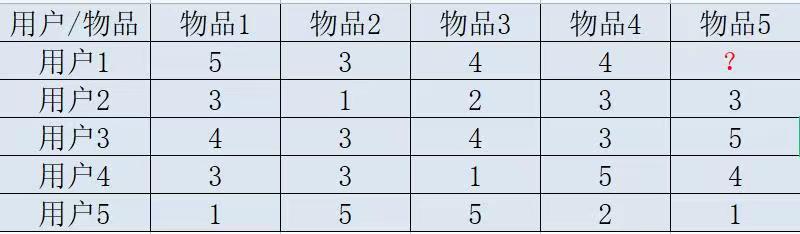
给用户推荐物品的过程可以形象的理解为上述用户对物品的喜欢程度，打分越高，说明用户对这个物品越喜欢。

UserCF的两个步骤

首先根据已有用户的打分情况计算一下用户1和用户 2， 3， 4，5的相似度，找出与用户1最相似的 n 个用户；

然后根据这 n 个用户对物品5的评分情况和与用户1的相似程度计算出用户1对物品5的评分，如果评分比较高的话，就把物品5推荐给用户1，否则不推荐。

2.2 相似度计算方式

计算相似度需要根据数据特点的不同选择不同的计算方法，下面给大家介绍三种常用的相似度计算方法：

2.2.1 余弦相似度

$sim(A,B)=cos(A,B)=\frac{A\cdot B}{\left \| A \right \|\cdot \left \| B \right \|}$

余弦相似度同样适用于n维向量，可以表示为

$cos\theta =\frac{\sum_{i=1}^{n}(Ai\times Bi)}{\sqrt{\sum_{i=1}^{n}(Ai)^{2}}\sqrt{\sum_{i=1}^{n}(Bi)^{2}}}$

2.2.2 杰卡德相似系数

集合A和B交集元素的个数在A、B并集中所占的比例，称为两个集合的杰卡德系数，用符号 J(A,B) 表示。杰卡德相似系数是衡量两个集合相似度的一种指标，jaccard值越大说明相似度越高。

$J(A,B)=\frac{\left | A\cap B \right |}{\left | A\cup B \right |}$

2.2.3 皮尔逊相关系数

相比余弦相似度，皮尔逊相关系数通过使用用户平均分对各独立评分进行修正，减小了用户评分偏置的影响。公式为：

$sim(x1,x2)=\frac{\sum_{k=1}^{n}(x1k-\bar{x1})(x2k-\bar{x2})}{\sqrt{\sum_{k=1}^{n}(x1k-\bar{x1})^{2}}\sqrt{\sum_{k=1}^{n}(x2k-\bar{x2})^{2}}}$

公式中， $x1k$ 代表用户1对物品k的评分， $\bar{x}$ 代表该用户对所有物品的平均分。

2.3 最终结果预测

根据上面的三种方法，我们可以计算出向量之间的相似度，也就是可以计算出用户与用户之间的相似度。这时候我们就可以选出与用户1最相近的n个用户，基于他们对物品5的评价计算出打分值，那么如何进行计算呢？

常用的计算方式也有很多，下面直接给大家介绍一种考虑更为全面的计算方式，利用用户相似度和该物品的评分与此用户的所有评分的差值进行加权平均。该公式考虑到了有的用户内心的评分标准不一的情况，即有的用户喜欢打高分，有的用户喜欢打低分的情况。公式如下

$Pi,j=\bar{Ri}+\frac{\sum_{k=1}^{n}(Si,k(Rk,j-\bar{Rk}))}{\sum_{k=1}^{n}Sj,k}$

下面对上面的例子具体实操一下

（1）计算用户1与其他四个用户的相似性（使用皮尔逊相关系数）：

用户1与用户2的余弦相似度：

$cosine(user1,user2)=\frac{5*3+3*1+4*2+4*3}{\sqrt{25+9+16+16}\sqrt{9+1+4+9}}=0.975$

用户1与用户2的皮尔逊相关系数：

user1（5，3，4，4） user2（3，1，2，3）

user1_ave = 4 user2_ave = 2.25

用各自的向量减去各自的平均值：

user1（1，-1，0，0） user2（0.75，-1.25，-0.25，0.75）

计算他们的余弦相似度：

$cos(user1,user2)=\frac{1*0.75+(-1)*(-1.25)+0*(-0.25)+0*0.75}{\sqrt{1+1+0+0}\sqrt{0.5625+1.5625+0.0625+0.5625}}=0.85$

根据以上计算得出用户1与用户2的相似度为0.85，同样方式可以计算出用户1与用户3、用户4、用户5的相似度分别为0.7，0，-0.79。如果n=2的话，那么与用户1最相似的两个用户为用户2和用户3，相似度分别为0.85和0.7

（2）根据相似度用户计算用户1对物品5的最终得分

用户2对物品5的评分是3，用户3对物品5的打分是5，那么根据上面的计算公式，可以计算出用户1对物品5的最终得分是

$Puser1,item5=\bar{R}user1+\frac{\sum_{k=1}^{2}(Suser1,userk(Ruserk,item5-\bar{R}userk))}{\sum_{k=1}^{2}Suser1,userk}=4+\frac{0.85*(3-2.4)+0.7*(5-3.8)}{0.85+0.7}=4.87$

（3）根据评分对用户进行推荐

由上述计算得，用户1对物品5的评分为4.87，根据用户1的评分得出物品推荐序列为

物品1>物品5>物品3=物品4>物品2

所以，如果要向用户1推荐两款物品，我们可以推荐物品1和物品5.

三、基于物品的协同过滤算法

物以类聚：预先根据其他用户的偏好数据计算出每个物品最相似的物品列表，然后为用户推荐与喜欢物品相类似的物品。

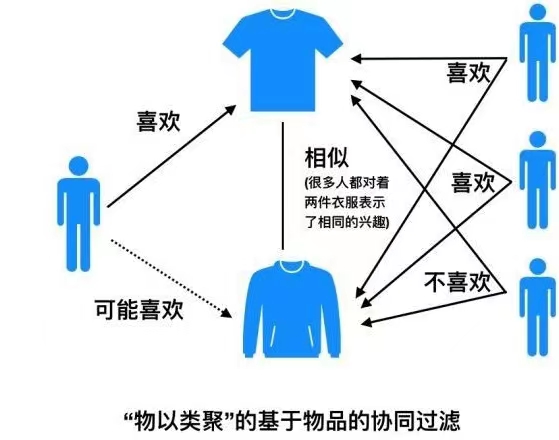
基于物品的协同过滤算法主要分为两个步骤：

（1）计算物品之间的相似度

（2）根据物品的相似度和用户的历史行为给用户生成推荐列表。

基于物品的协同过滤算法跟基于用户的协同过滤算法计算过程类似，因此我们继续使用上述例子进行计算。

算法步骤为：

（1）首先计算一下物品5和物品1， 2， 3， 4之间的相似度

物品向量：

item1（3，4，3，1）；item2（1，3，3，5）；item3（2，4，1，5）；item4（3，3，5，2）

item5（3，5，4，1）

物品5与物品1的余弦相似度：

$cosine(item1,item5)=\frac{3*3+4*5+3*4+1*1}{\sqrt{9+16+9+1}*\sqrt{9+25+16+1}}=0.994$

物品5与物品1的皮尔逊相关系数：

item1_ave = 2.75 item5_ave = 3.25

用各自的向量减去各自的平均值：

item1（0.25，1.25，0.25，-1.75） item5（-0.25，1.75，0.75，-2.25）

计算他们的余弦相似度(同上述相似度计算公式，直接代入即可）

$cosine(item1,item5)=0.9694$

根据以上计算得出物品5和物品1的相似度为0.9694，同样方式计算出物品5和物品2、物品3、物品4的相似度分别为：-0.478、-0.4276、0.5816。如果n=2的话，那么与物品5最相似的两个物品为物品1和物品4，相似度分别为0.9694和0.5816。

（2）计算对物品5的打分情况

$Puser1,item5=\frac{\bar{R}item5+\sum_{k=1}^{2}()Sitem5,itemk(Ruser1,itemk-\bar{R}itemk)}{\sum_{k=1}^{2}Sitemk,item5}=\frac{13}{4}+\frac{0.97*(5-3.2)+0.58*(4-3.4)}{0.97+0.58}=4.6$

（3）根据评分对用户进行推荐

由上述计算得，用户1对物品5的评分为4.6，根据用户1的评分得出物品推荐序列为

物品1>物品5>物品3=物品4>物品2

所以，如果要向用户1推荐两款物品，我们可以向用户1推荐物品1和物品5。

四、上代码

4.1 UserCF

1、先建立数据表


def loadData():
    users = {'user1': {'1': 5, '2': 3, '3': 4, '4': 4},
             'user2': {'1': 3, '2': 1, '3': 2, '4': 3, '5': 3},
             'user3': {'1': 4, '2': 3, '3': 4, '4': 3, '5': 5},
             'user4': {'1': 3, '2': 3, '3': 1, '4': 5, '5': 4},
             'user5': {'1': 1, '2': 5, '3': 5, '4': 2, '5': 1}
             }
    return users

2、计算用户相似性矩阵


user_data = loadData()
similarity_matrix = pd.DataFrame(
    np.identity(len(user_data)), # identity函数用于一个n*n的单位矩阵(主对角线元素全为1，其余全为0的矩阵)。
    index=user_data.keys(),
    columns=user_data.keys(),
)
 
# 遍历每条用户-物品评分数据
for u1, items1 in user_data.items():
    for u2, items2 in user_data.items():
        # 跳过user相同的情况，为1
        if u1 == u2:
            continue
        vec1, vec2 = [], []
        # 遍历user1的所有items
        for item, rating1 in items1.items():
            # 与user2相应的item
            rating2 = items2.get(item, -1) # dict的get
            if rating2 == -1:
                continue
            vec1.append(rating1)
            vec2.append(rating2)
        # 利用user1和user2的items，计算不同用户之间的皮尔逊相关系数
        similarity_matrix[u1][u2] = np.corrcoef(vec1, vec2)[0][1] # vec1和vec2的相关性
 
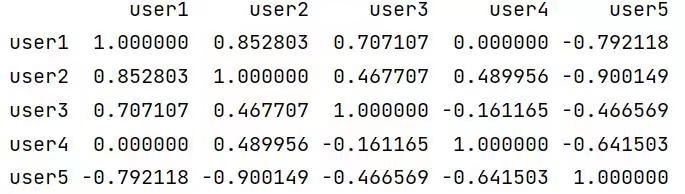
print(similarity_matrix)

运行结果：

3、计算与用户1最为相似的n个用户


target_user = 'user1'
num = 2
 
# 由于最相似的用户为自己，去除本身
sim_users = similarity_matrix[target_user].sort_values(ascending=False)[1:num+1].index.tolist()
print(f'与用户{target_user}最相似的{num}个用户为：{sim_users}')

运行结果：

4、预测用户1对物品5的评分


weighted_scores = 0.
corr_values_sum = 0.
 
target_item = '5'
# 基于皮尔逊相关系数预测用户评分
for user in sim_users:
    corr_value = similarity_matrix[target_user][user] # 目标与当前user的相关系数
    user_mean_rating = np.mean(list(user_data[user].values())) # 当前user的评分平均值
 
    weighted_scores += corr_value * (user_data[user][target_item] - user_mean_rating) # 权重*(评分-平均)，累加
    corr_values_sum += corr_value # 相关系数之和，分母
 
target_user_mean_rating = np.mean(list(user_data[target_user].values())) # 目标的评分平均值
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum # 最后结果
print(f'{target_user}对物品{target_item}的预测评分为：{target_item_pred}')

运行结果：

4.2 ItemCF

1、先建立数据表


def loadData():
    items = {'1': {'user1': 5.0, 'user2': 3.0, 'user3': 4.0, 'user4': 3.0, 'user5': 1.0},
             '2': {'user1': 3.0, 'user2': 1.0, 'user3': 3.0, 'user4': 3.0, 'user5': 5.0},
             '3': {'user1': 4.0, 'user2': 2.0, 'user3': 4.0, 'user4': 1.0, 'user5': 5.0},
             '4': {'user1': 4.0, 'user2': 3.0, 'user3': 3.0, 'user4': 5.0, 'user5': 2.0},
             '5': {'user2': 3.0, 'user3': 5.0, 'user4': 4.0, 'user5': 1.0}
             }
    return items

2、计算物品相似性矩阵


item_data = loadData()
 
similarity_matrix = pd.DataFrame(
    np.identity(len(item_data)),
    index=item_data.keys(),
    columns=item_data.keys(),
)
 
# 遍历每条物品-用户评分数据
for i1, users1 in item_data.items():
    for i2, users2 in item_data.items():
        if i1 == i2:
            continue
        vec1, vec2 = [], []
        for user, rating1 in users1.items():
            rating2 = users2.get(user, -1)
            if rating2 == -1:
                continue
            vec1.append(rating1)
            vec2.append(rating2)
        similarity_matrix[i1][i2] = np.corrcoef(vec1, vec2)[0][1]
 
print(similarity_matrix)

运行结果：

3、计算与物品5最为相似的n个用户


target_user = 'user1'
target_item = '5'
num = 2
 
sim_items = []
sim_items_list = similarity_matrix[target_item].sort_values(ascending=False).index.tolist()
for item in sim_items_list:
    # 如果target_user对物品item评分过
    if target_user in item_data[item]:
        sim_items.append(item)
    if len(sim_items) == num:
        break
print(f'与物品{target_item}最相似的{num}个物品为：{sim_items}')

运行结果：

4、预测用户1对物品5的评分


target_user_mean_rating = np.mean(list(item_data[target_item].values()))
weighted_scores = 0.
corr_values_sum = 0.
 
target_item = '5'
for item in sim_items:
    corr_value = similarity_matrix[target_item][item]
    user_mean_rating = np.mean(list(item_data[item].values()))
 
    weighted_scores += corr_value * (item_data[item][target_user] - user_mean_rating)
    corr_values_sum += corr_value
 
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
print(f'用户{target_user}对物品{target_item}的预测评分为：{target_item_pred}')

运行结果：

五、协同过滤算法的问题分析

目前，协同过滤技术得到了广泛应用。但是随着网站商品信息量和用户人数的不断攀升，网站的结构也越来越复杂。通过对协同过滤技术以及推荐系统的研究，我们发现协同过滤技术的实现中存在的问题主要有以下几点。

5.1 稀疏性问题

稀疏性问题是推荐系统面临的主要问题。比如在一些大型电子商务购买系统，用户购买过的数量相对网站中商品数量可谓是冰山一角，这就导致了用户评分矩阵的数据非常稀疏，进行相似性计算耗费会很大，也难以找到相邻用户数据集，从而使得推荐系统的推荐质量急剧下降。

5.2 冷启动问题

因为传统的协同过滤推荐是基于用户/物品的相似性计算来得到目标用户的推荐，在一个新的项目首次出现的时候，因为没有用户对它作过评价，因此单纯的协同过滤无法对其进行预测评分和推荐。而且，由于新项目出现早期，用户评价较少，推荐的准确性也比较差。

5.3 可扩展性问题

面对日益增多的数据量，算法的扩展性问题成为制约推荐系统实施的重要因素。识别“最近邻居”算法的计算量随着用户和项的增加而大大增加，对于上百万的数目，通常的算法会遇到严重的扩展性瓶颈问题。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/627016

经典推荐算法之协同过滤_协同过滤算法

一、 协同过滤算法简介

二、 基于用户的协同过滤算法

2.1 实例

2.2 相似度计算方式

2.2.1 余弦相似度

2.2.2 杰卡德相似系数

2.2.3 皮尔逊相关系数

2.3 最终结果预测

三、 基于物品的协同过滤算法

四、 上代码

4.1 UserCF

4.2 ItemCF

五、 协同过滤算法的问题分析

5.1 稀疏性问题

5.2 冷启动问题

5.3 可扩展性问题

一、协同过滤算法简介

二、基于用户的协同过滤算法

三、基于物品的协同过滤算法

四、上代码

五、协同过滤算法的问题分析