当前位置: article > 正文

贝叶斯滤波_∑yp(x,y)等于什么

作者：笔触狂放9 | 2024-06-02 19:31:24

踩

∑yp(x,y)等于什么

转载自：http://www.cnblogs.com/ycwang16/p/5995702.html

认知计算，还要从贝叶斯滤波的基本思想讲起。这一部分，我们先回顾贝叶斯公式的数学基础，然后再来介绍贝叶斯滤波器。

(一). 概率基础回顾

我们先来回顾一下概率论里的基本知识：

1. XX: 表示一个随机变量，如果它有有限个可能的取值{x1,x2,⋯,xn}{x1,x2,⋯,xn}.

2. p(X=xi)p(X=xi):表示变量XX的值为 xixi的概率。

3. p(⋅)p(⋅):称为概率质量函数(probability mass function).

例如：一个家里有3个房间，机器人在各个房间的概率为 p(room)={0.1,0.3,0.6}p(room)={0.1,0.3,0.6}.

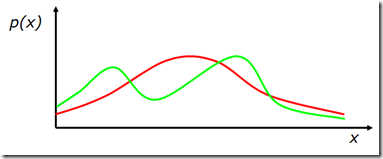
4. 如果XX在连续空间取值，p(x)p(x)称为概率密度函数(probability density function)，

p(x∈(a,b))=∫abp(x)dxp(x∈(a,b))=∫abp(x)dx

图1. 概率密度函数曲线示例

5. 联合概率：p(X=x and Y=y)=p(x,y)p(X=x and Y=y)=p(x,y)，称为联合概率密度分布。如果XX和YY是相互独立的随机变量，p(x,y)=p(x)p(y)p(x,y)=p(x)p(y)。

6. 条件概率：p(X=x|Y=y)p(X=x|Y=y) 是在已知Y=yY=y的条件下，计算X=xX=x的概率。

p(x|y)=p(x,y)/p(y)p(x|y)=p(x,y)/p(y)

p(x,y)=p(x|y)p(y)=p(y|x)p(x)p(x,y)=p(x|y)p(y)=p(y|x)p(x)

如果xx和yy相互独立，则：

p(x|y)=p(x)p(x|y)=p(x)

7. 全概率公式：

离散情况下:

p(x)=∑yp(x,y)=∑yp(x|y)p(y)p(x)=∑yp(x,y)=∑yp(x|y)p(y)

连续情况下：

p(x)=∫p(x,y)dy=∫p(x|y)p(y)dyp(x)=∫p(x,y)dy=∫p(x|y)p(y)dy

(二). 贝叶斯公式

2.1 贝叶斯公式

基于条件概率公式和全概率公式，我们可以导出贝叶斯公式：

这里面xx一般是某种状态；yy一般是代表某种观测。
我们称P(y|x)P(y|x)为causal knowledge，意即由xx的已知情况，就可以推算yy发生的概率，例如在图2的例子中，已知如果门开着，则z=0.5mz=0.5m的概率为0.6；如果门关着，则z=0.5mz=0.5m的的概率为0.3。
我们称P(x)P(x)为prior knowledge，是对xx的概率的先验知识。例如在图2的例子中，可设门开或关的概率各占50%50%.
P(x|y)P(x|y)是基于观测对状态的诊断或推断。贝叶斯公式的本质就是利用causal knowledge和prior knowledge来进行状态推断或推理。

例1: Dog face ：

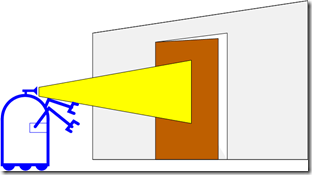
在图2所示的例子中，机器人根据观测的到门的距离，估算门开或关的概率，若测量到门的距离为z=0.5mz=0.5m，则可用条件概率描述门开着的概率：

P(open|z=0.6)=?P(open|z=0.6)=?

图 2.机器人根据观测计算门开或关的概率

2.2 贝叶斯公式的计算

可以看到贝叶斯公式的分母项P(y)P(y)，同P(x|y)P(x|y)无关，所以可以把它作为归一化系数看待：

P(x|y)=P(y|x)P(x)P(y)=ηP(y|x)P(x)η=P(y)−1=1∑xP(y|x)P(x)P(x|y)=P(y|x)P(x)P(y)=ηP(y|x)P(x)η=P(y)−1=1∑xP(y|x)P(x)

所以基于causal knowledge和prior knowledge进行条件概率计算的过程如下：

Algorithm:

2.3 贝叶斯公式中融合多种观测

在很多应用问题中，我们会用多种观测信息对一个状态进行猜测和推理，贝叶斯公式中是如何融合多种观测的呢？

我们简单推导一下：

所以有：

P(x|y,z)=P(y|x,z)P(x|z)P(y|z)P(x|y,z)=P(y|x,z)P(x|z)P(y|z)

2.4 贝叶斯递推公式

由此，我们来推导贝叶斯滤波的递推公式：

P(x|z1,…,zn)=?P(x|z1,…,zn)=?

我们把znzn看做yy，把z1,…,zn−1z1,…,zn−1看做zz，代入上面的公式：

再由Markov属性，在xx已知的情况下，znzn同{z1,…,zn–1}{z1,…,zn–1}无关，所以：

从而我们得到贝叶斯的递推公式：

例2： Dog face 在例1的基础上，如果机器人第二次测量到门的距离仍然为0.5米，计算门开着的概率。

所以，第二次z=0.5m的观测增大了对门开着的概率的置信程度。

(三). 如何融入动作？

在实际问题中，对象总是处在一个动态变化的环境中，例如：

机器人自身的动作影响了环境状态
其它对象，比如人的动作影响了环境状态
或者就是简单的环境状态随着时间发生了变化。

如何在Bayes模型中来描述动作的影响呢?

首先，动作所带来的影响也总是具有不确定性的
其次，相比于观测，动作一般会使得对象的状态更为模糊（或更不确定）。

我们用uu来描述动作，在x′x′状态下，执行了动作uu之后，对象状态改变为xx的概率表述为：

P(x|u,x′)P(x|u,x′)

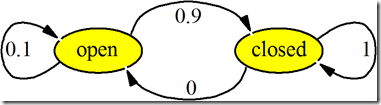
动作对状态的影响一般由状态转移模型来描述。如图3所示，表示了“关门”这个动作对状态影响的转移模型。这个状态转移模型表示：关门这个动作有0.1的失败概率，所以当门是open状态时，执行“关门”动作，门有0.9的概率转为closed状态，有0.1的概率保持在open状态。门是closed的状态下，执行“关门”动作，门仍然是关着的。

图3. “关门”动作的状态转移模型

执行某一动作后，计算动作后的状态概率，需要考虑动作之前的各种状态情况，把所有情况用全概率公式计算：

连续情况下：

P(x|u)=∫P(x|u,x′)P(x′)dx′P(x|u)=∫P(x|u,x′)P(x′)dx′

离散情况下：

P(x|u)=∑P(x|u,x′)P(x′)P(x|u)=∑P(x|u,x′)P(x′)

例3： Dog face 在例2的基础上，如果按照图3所示的状态转移关系，机器人执行了一次关门动作，计算动作后门开着的概率？

所以，执行一次关门动作后，门开着的概率变为了0.08.

(四). 贝叶斯滤波算法

4.1 算法设定

由上述推导和示例，我们可以给出贝叶斯滤波的算法，算法的输入输出设定如下。

系统输入
1. 1到tt时刻的状态观测和动作：dt={u1,z1…,ut,zt}dt={u1,z1…,ut,zt}
2. 观测模型：P(z|x)P(z|x)
3. 动作的状态转移模型：P(x|u,x′)P(x|u,x′)
4. 系统状态的先验概率分布P(x)P(x).
期望输出
1. 计算状态的后延概率，称为状态的置信概率：Bel(xt)=P(xt|u1,z1…,ut,zt)Bel(xt)=P(xt|u1,z1…,ut,zt)

4.2 算法基本假设

贝叶斯滤波的基本假设：

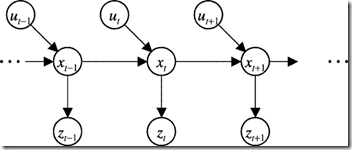
1. Markov性假设: tt时刻的状态由t−1t−1时刻的状态和tt时刻的动作决定。tt时刻的观测仅同tt时刻的状态相关，如图4所示：

图4. Markov模型

2. 静态环境，即对象周边的环境假设是不变的

3. 观测噪声、模型噪声等是相互独立的

4.3 Bayes滤波算法

基于上述设定和假设，我们给出贝叶斯滤波算法的推导过程：

Bel(xt)=P(xt|u1,z1…,ut,zt)Bel(xt)=P(xt|u1,z1…,ut,zt)

=ηP(zt|xt,u1,z1,…,ut)P(xt|u1,z1,…,ut) <—Bayes=ηP(zt|xt,u1,z1,…,ut)P(xt|u1,z1,…,ut) <—Bayes

=ηP(zt|xt)P(xt|u1,z1,…,ut) <—Markov=ηP(zt|xt)P(xt|u1,z1,…,ut) <—Markov

=ηP(zt|xt)∫P(xt|ut,xt−1)Bel(xt−1)dxt−1=ηP(zt|xt)∫P(xt|ut,xt−1)Bel(xt−1)dxt−1

其中第一步采用贝叶斯公式展开，第二步使用Markov性质(ztzt仅由xtxt决定)；第三步使用全概率公式对xt−1xt−1进行展开；第四步继续使用Markov性质(xtxt仅由xt−1xt−1和utut决定)；第五步继续使用Markov性质，因为xt−1xt−1同utut无关，最终得到Bel(xt)Bel(xt)的递推公式。

可见递推公式中分为两个步骤，∫P(xt|ut,xt−1)Bel(xt−1)dxt−1∫P(xt|ut,xt−1)Bel(xt−1)dxt−1部分是基于xt−1,utxt−1,ut预测xtxt的状态；ηP(zt|xt)ηP(zt|xt)部分是基于观测ztzt更新状态xtxt.

4.3 Bayes滤波算法流程

所以，Bayes滤波的算法流程图如图5所示。如果dd是观测，则进行一次状态更新，如果dd是动作，则进行一次状态预测。

图5. Bayes滤波的算法流程

我们看到，在进行状态预测时，需要对所有可能的x′x′状态进行遍历，使得基本的Bayes模型在计算上成本是较高的。

4.3 Bayes滤波算法的应用

Bayes滤波方法是很多实用算法的基础，例如：

Kalman滤波
扩展Kalman滤波
信息滤波
粒子滤波

等，我们在下一节介绍Kalman滤波。

参考文献

[1]. Sebastian Thrun, Wolfram Burgard, Dieter Fox, Probabilistic Robotics, 2002, The MIT Press.

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/664062