Interpretable Machine Learning中GLM，GAM等_glm与gam

关于GLM，GAM等的描述
线性回归模型的最大优势也是最大的弱点是预测被建模为特征的加权和。此外，线性模型还有许多其他假设。所有这些假设在实际中经常被违反的坏消息是给定特征的结果可能具有非高斯分布，特征可能相互作用，特征与结果之间的关系可能是非线性的。好消息是，统计界已经开发了各种修改，将线性回归模型从简单的刀片转换为瑞士刀。

如广义线性模型（GLM）和广义加法模型（GAM）可扩展线性模型。
让记住线性回归模型的公式：

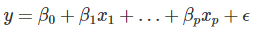
线性回归模型假设实例的结果y可以通过其p特征的加权和以及遵循高斯分布的单个误差ε来表示。 通过将数据强制转换为公式的紧身胸衣，我们获得了大量的模型可解释性。 特征效应是相加的，意味着没有相互作用，并且关系是线性的，意味着特征的增加可以直接转化为预测结果的增加/减少。 线性模型允许我们将特征和预期结果之间的关系压缩为单个数字，即估计的权重。

但是，对于许多现实世界的预测问题，简单的加权和过于严格。 在本章中，我们将了解经典线性回归模型的三个问题以及如何解决它们。 可能违反假设的问题还有很多，但我们将重点关注以下三个问题：

问题1：给定特征的目标结果y不遵循高斯分布。
示例：假设我想预测在给定的一天骑自行车的时间。作为特征我有一天的类型，天气等。如果我使用线性模型，它可以预测负分钟，因为它假定高斯分布不会在0分钟停止。此外，如果我想用线性模型预测概率，我可以得到负数或大于1的概率。
解决方案：广义线性模型（GLM）。

问题2：这些特征相