笔触狂放9

这个屌丝很懒，什么也没留下！

热门标签

链式二叉树的代码实现_二叉树链式存储结构代码

作者：笔触狂放9 | 2024-06-16 15:09:58

踩

二叉树链式存储结构代码

二叉树的存储结构：

1. 顺序存储 ：顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

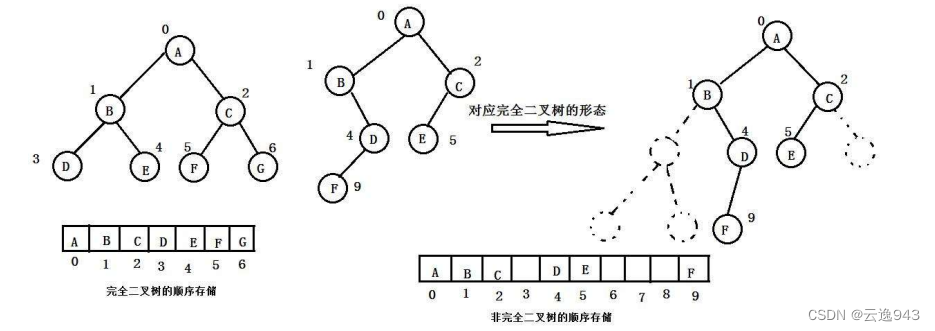
2. 链式存储 ：二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链，三叉比较复杂，所以在下面对二叉树的代码实现用的都是二叉链表的方式进行的实现。

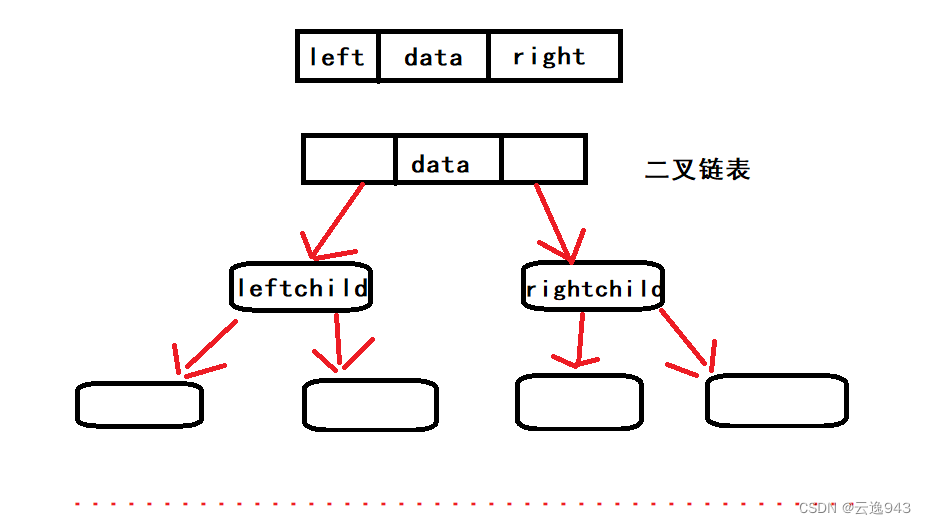
链式二叉树的实现

1.二叉树的结构体类型


typedef int BTDataType;
typedef struct BinaryTreeNode {
	BTDataType data;	//二叉树节点的值
	struct BinaryTreeNode* left;	//二叉树的左指针——指向它的左孩子
	struct BinaryTreeNode* right;	//二叉树的右指针——指向它的右孩子
}BTNode;    //重定义了二叉树的类型名称为BTNode

2.创建二叉树结点

以下代码是根据该图进行实现：

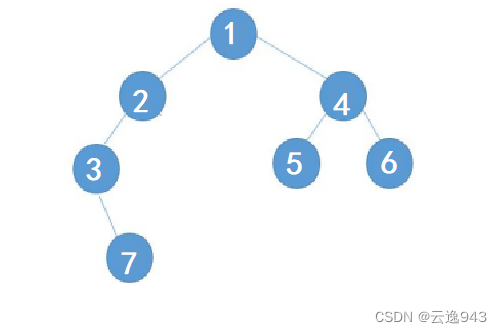
代码实现：


//创建二叉树
BTNode* TreeCreate() {
 
    //动态开辟所需要的结点
	BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
	assert(n1);    //assert作用断言，判断动态开辟是否成功！
 
	BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
	assert(n2);
	BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
	assert(n3);
	BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
	assert(n4);
	BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
	assert(n5);
	BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
	assert(n6);
	BTNode* n7 = (BTNode*)malloc(sizeof(BTNode));
	assert(n7);
 
    //创建好后，给各结点赋值
	n1->data = 1;
	n2->data = 2;
	n3->data = 3;
	n4->data = 4;
	n5->data = 5;
	n6->data = 6;
	n7->data = 7;
 
    
    //给各节点的左右指针指明方向，形成二叉树
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n2->right = NULL;
	n3->left = NULL;
	n3->right = n7;
	n7->left= NULL;
	n7->right = NULL;
	n4->left = n5;
	n4->right = n6;
	n5->left = NULL;
	n5->right =NULL;
	n6->left = NULL;
	n6->right = NULL;
 
    //形成二叉树后，返回让指针返回根节点
	return n1;
 
}

3.二叉树的前序遍历

.前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

口诀：先遍历根，再遍历左子树，最后遍历右子树。


//二叉树的前序遍历
void PreOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历根
	printf("%d  ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

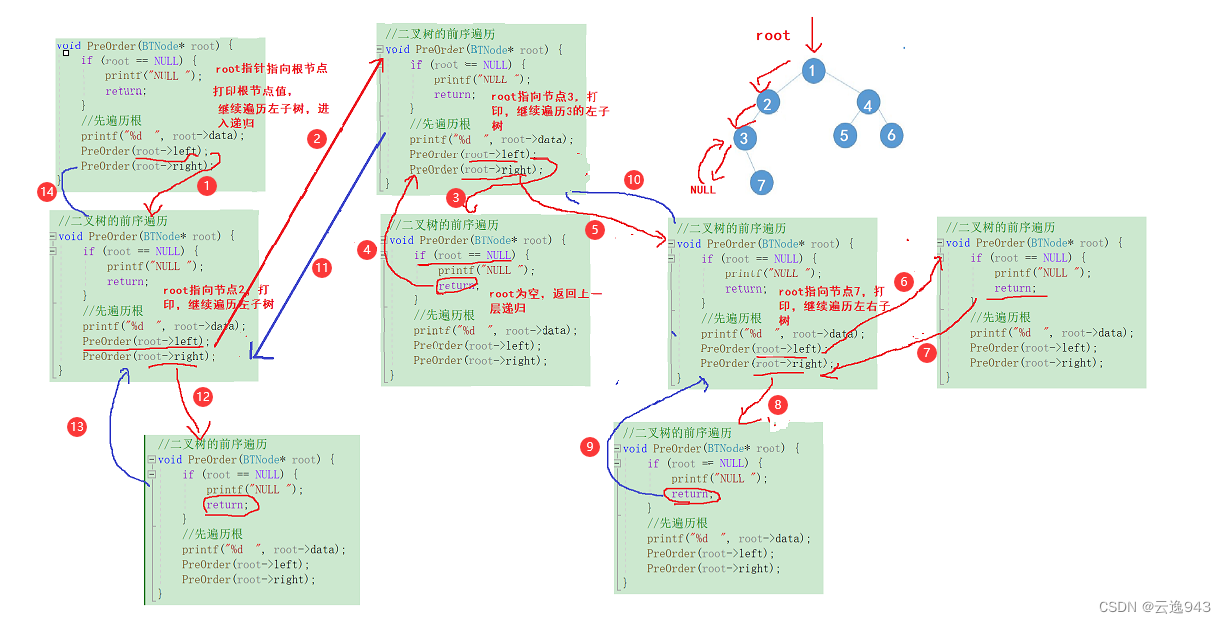
上图为部分递归图解，过程：root先指向根节点，打印1，接着进入递归，root->left，指向节点2，打印节点值，再进入递归，root->left，指向节点3，打印3，再进行递归，root->left，发现为空，打印NULL后返回节点3，进而递归root->right，指向节点7，再对7的左右节点进行递归......，注：每次递归完了都会返回上一层，继续执行上一层的下一句代码......

测试结果：

4.二叉树的中序遍历

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

口诀：先遍历左子树，再遍历根，最后遍历右子树


//二叉树的中序遍历
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历左子树，再根，再右
	InOrder(root->left);
	printf("%d  ", root->data);
	InOrder(root->right);
}

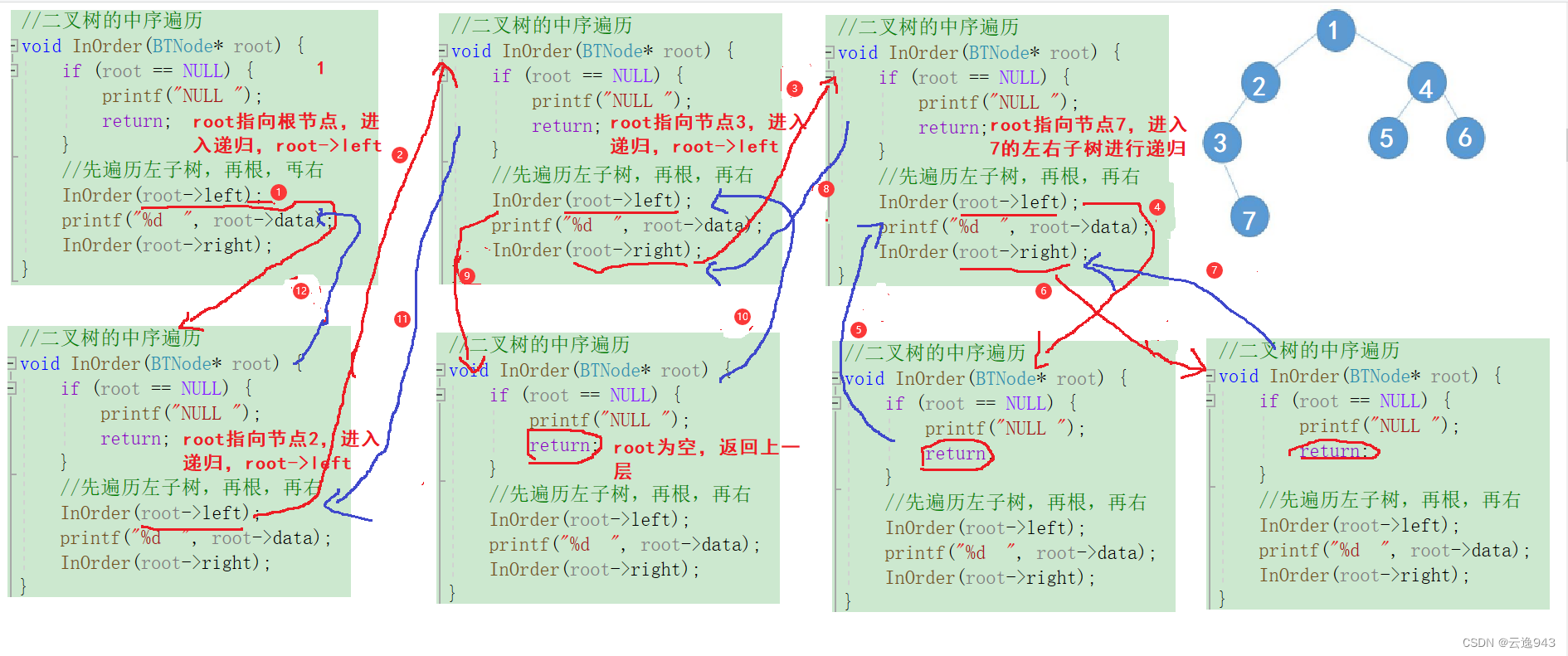
上图为部分递归图解，过程：root先指向根节点，进入递归，root->left，指向节点2，再进入递归root->left，指向节点3，再进行递归root->left，发现为空，打印NULL后返回节点3，打印节点值3，进而递归root->right，指向节点7，再对7的左右节点进行递归......发现都为空，返回节点3，节点3递归完成，继续返回上一层节点2的递归，打印节点2，进而递归root->right，为空，返回节点2，节点2递归完成，返回节点1，打印节点1，进而递归节点1的root->right......

测试结果：

5.二叉树的后序遍历

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

口诀：先遍历左子树，再遍历右子树，最后遍历根节点。


//二叉树的后序遍历
void PostOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历左子树，再右，最后根
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d  ", root->data);
}

后序遍历，自己画图理解吧~~

测试结果：

6.求二叉树的总结点个数

错误写法：


//统计二叉树的所有节点个数—-错误写法
 
void  BinaryTreeSize2(BTNode* root) {
    static int count = 0;
	if (root == NULL)
		return ;
 
    //遇到节点先统计++
	++count;
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
 
}

//使用static延长局部变量的生命周期，出了作用域不会被销毁，仍会累计个数。但这种静态操作，只能调用一次，多次调用会把上一次的结果也累计上，得出错误的答案，所以这种写法并不可取，链式二叉树大多是递归形式进行定义，那么需要分而治之！将大问题化解成多个小问题，然后各个击破！

举个例子：学校需要清点这两天来到学校的学生和老师人数，需要院长将计算机系和会计系的总人数报上去，那么有两种方法，其一：院长一个班一个班的进行遍历统计，最后报回总人数；其二，院长让两个系的主任去统计，然后两个系的主任让班主任去统计，班主任再让班长去统计各班的人数。院长的任务就是把两个系主任统计出的名单加起来，最后报上去。而第二种方法相比第一种是非常简便的，只需要让级别小的去统计，然后将它们返回的结果相加再报给上级即可。这就是分而治之！！！

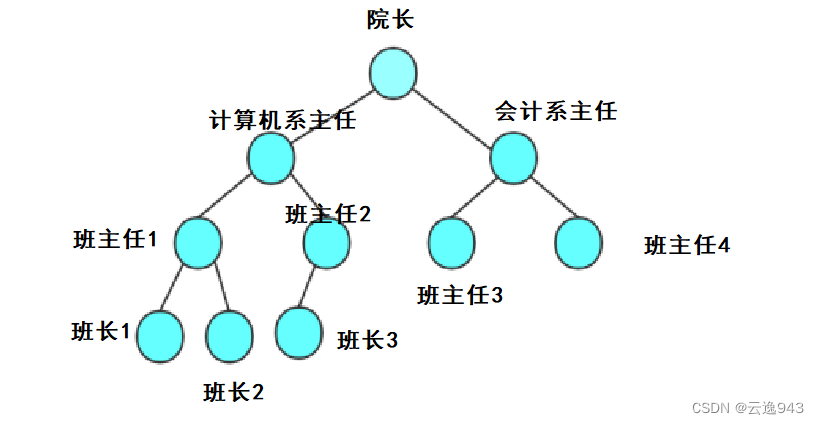
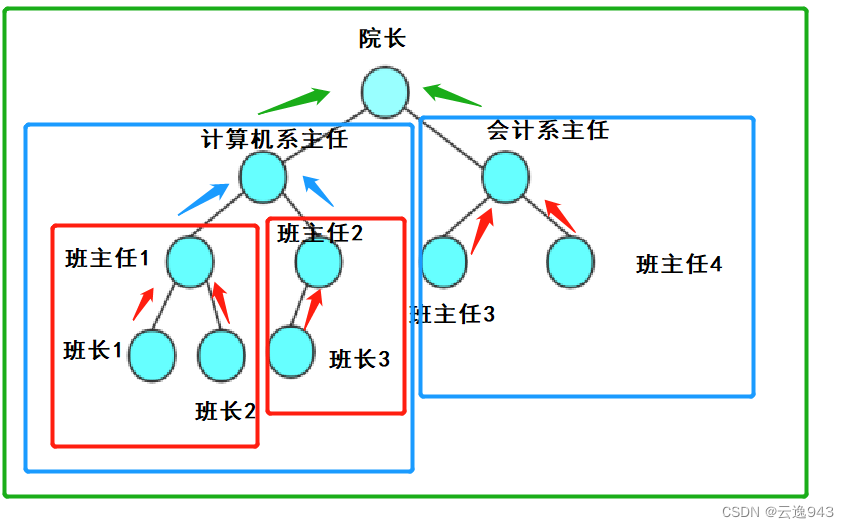
所以正确的代码实现：


//统计二叉树的所有节点个数——分而治之（大事化小，小事化了）
int BinaryTreeSize(BTNode* root) {
	return root == NULL ? 0 : 
		BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

先统计该节点的左子树部分的节点数，进而统计该节点的右子树部分的节点数，最后把两树相加，再把自己算上即可。

测试结果：

7.求二叉树的叶子节点个数

实现该功能仍是用到了分而治之的算法，先让各个小弟把活干好，我们这个大哥只需要拿到成果即可~哈哈哈！


//统计二叉树的叶子节点个数
int BinaryTreeleaf(BTNode* root) {
	if (root == NULL) {
		return 0;
	}
 
	if (root->left == NULL && root->right == NULL)
		return 1;
 
	return BinaryTreeleaf(root->left) + BinaryTreeleaf(root->right);
}

测试结果：

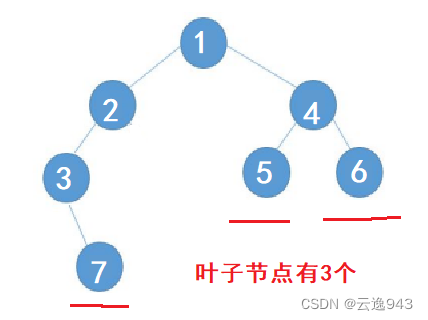
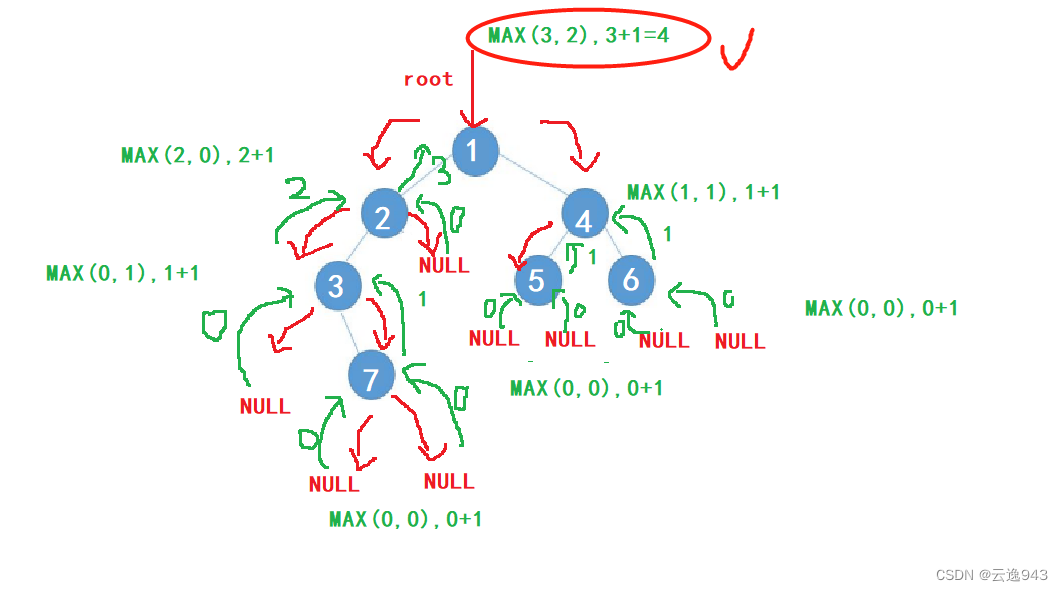
8.求二叉树的高度层次

该功能实现的思路是要计算出左子树层次高度和右子树层次高度，取出较大的那个高度，然后+1就是该二叉树的高度层次。


//计算二叉树的高度层次
int BinaryTreeHigh(BTNode* root) {
	if (root == NULL)
		return 0;
	int leftHigh = BinaryTreeHigh(root->left);
	int rightHigh = BinaryTreeHigh(root->right);
	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}

测试结果：

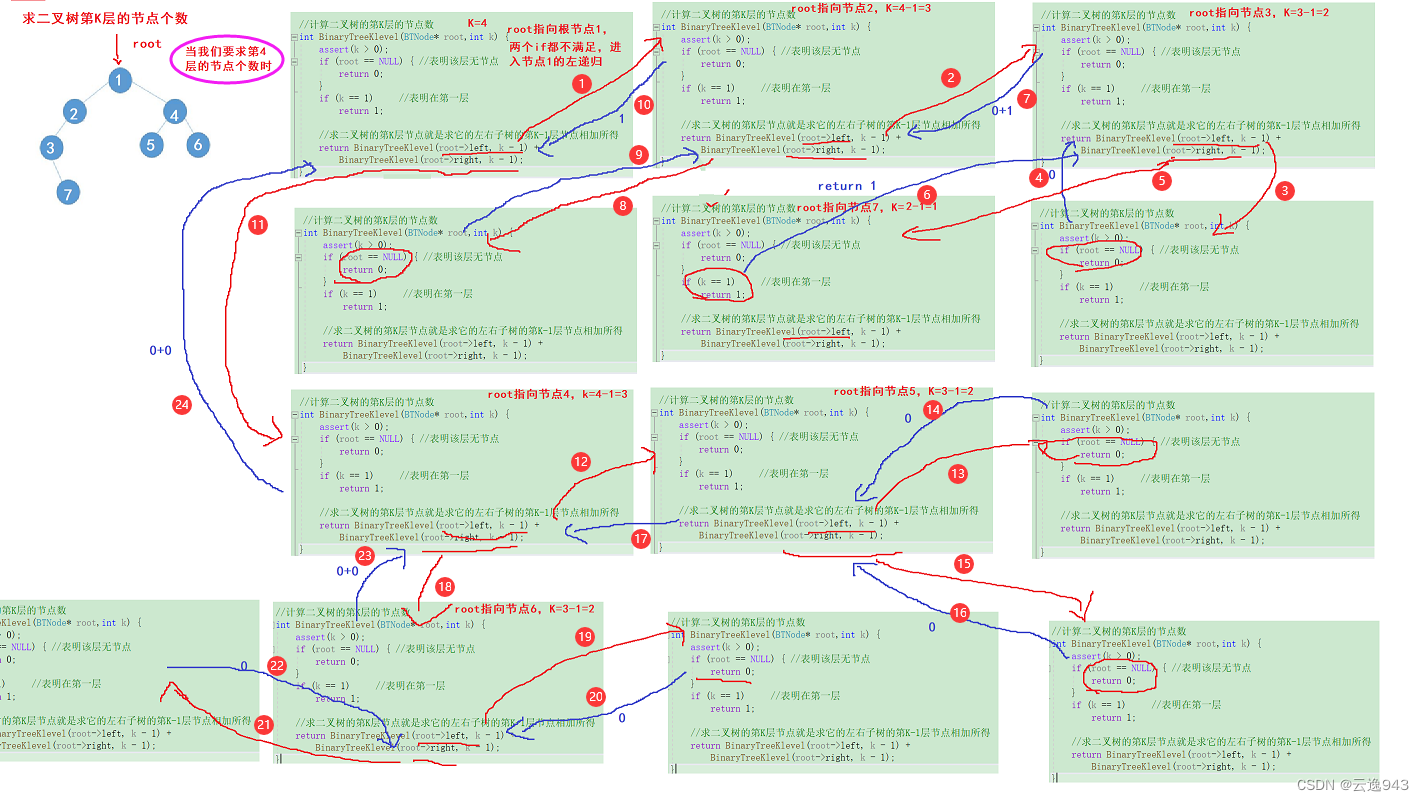
9.求二叉树第K层的节点个数

这个功能也是使用递归实现，求二叉树第K层的节点个数就是求该二叉树的左子树第K-1层的节点个数+该二叉树的右子树第K-1层的节点个数，仍然是递归的核心思路，大问题划分成多个小问题去求解！


//计算二叉树的第K层的节点数
int BinaryTreeKlevel(BTNode* root,int k) {
	assert(k > 0);
	if (root == NULL) {	//表明该层无节点
		return 0;
	}
	if (k == 1)		//表明在第一层
		return 1;
 
	//求二叉树的第K层节点就是求它的左右子树的第K-1层节点相加所得
	return BinaryTreeKlevel(root->left, k - 1) +
		BinaryTreeKlevel(root->right, k - 1);
}

测试结果：

10.查找二叉树某个节点的值

我在实习该功能的核心思路是使用先序遍历，先看根节点的值是否和要找的节点值相同，若不相同则使用递归去寻找根的左子树值，左子树部分全部找完也没找到，就去右子树部分去寻找，若两边都没有，则返回空。


/查找二叉树某个节点的值
BTNode* TreeFind(BTNode* root, BTDataType x) {
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	//先从左子树开始
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
		return lret;
 
	//找不到后再从右子树开始
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
		return rret;
	//两边都找不到后，返回空
	return NULL;
}

测试结果：

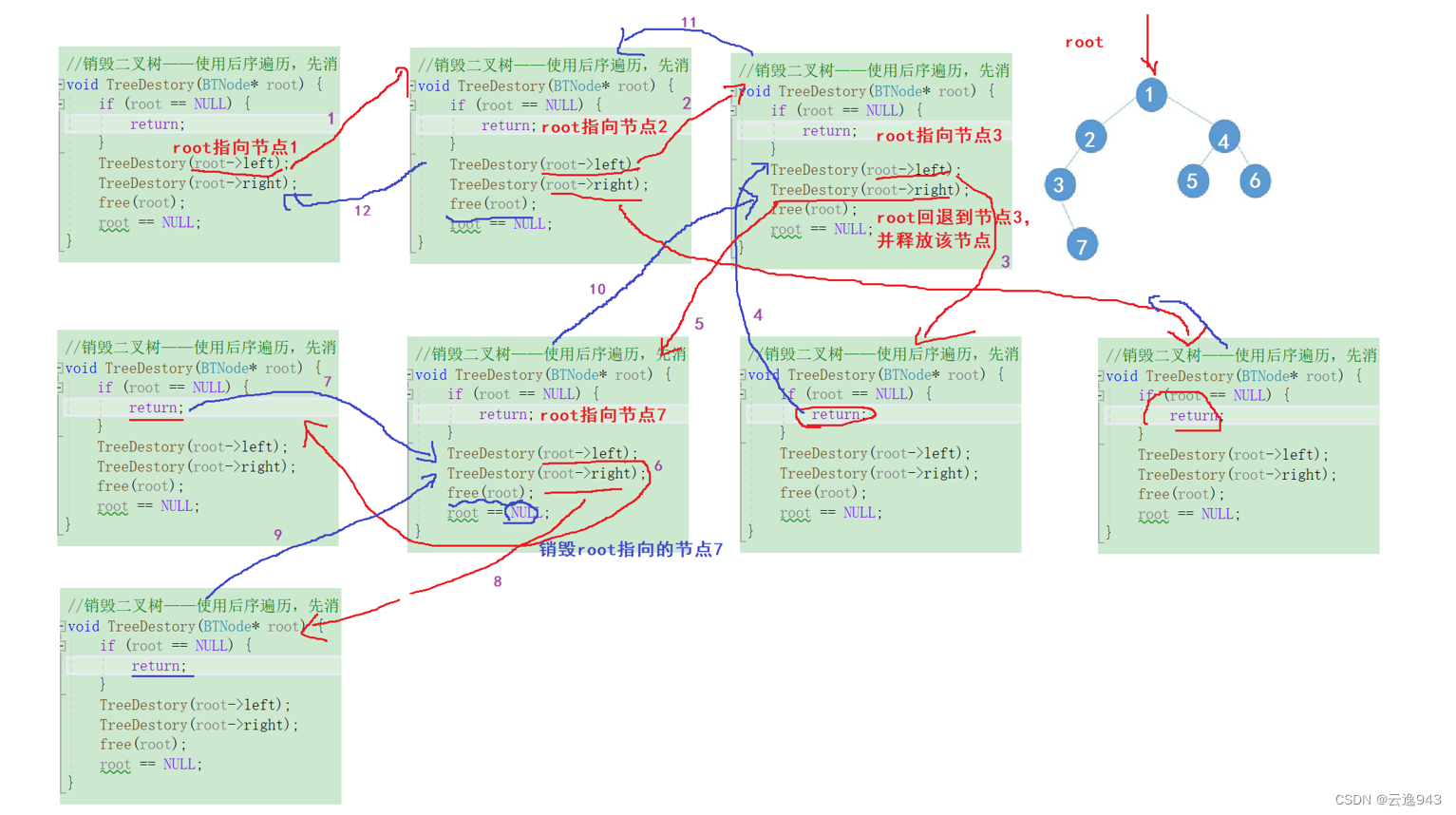
11.二叉树的销毁


//销毁二叉树——使用后序遍历，先消除左右子树，最后消除跟节点（从下到上）
void TreeDestory(BTNode* root) {
	if (root == NULL) {
		return;
	}
    //递归
	TreeDestory(root->left);
	TreeDestory(root->right);
	free(root);
	root == NULL;
}

该功能的实现：二叉树的销毁也是通过一层一层的向下递归，从下往上去释放节点。

注：不可直接删除根节点，因为二叉树是用链表构成的，删除了根节点，并不能删除它链接的左右子树节点，这些节点仍然存在，从而成为野指针，消耗内存，不可取！！！

完整的链式二叉树代码：

.h文件：


#pragma once
#include<assert.h>
#include<stdlib.h>
#include<stdio.h>
 
typedef int BTDataType;
typedef struct BinaryTreeNode {
	BTDataType data;	//二叉树节点的值
	struct BinaryTreeNode* left;	//二叉树的左指针——指向它的左孩子
	struct BinaryTreeNode* right;	//二叉树的右指针——指向它的右孩子
}BTNode;
 
//创建二叉树
BTNode* TreeCreate();
 
//二叉树的前序遍历
void PreOrder(BTNode* root);
 
//二叉树的中序遍历
void InOrder(BTNode* root);
 
//二叉树的后序遍历
void PostOrder(BTNode* root);
 
//统计二叉树的所有节点个数
int BinaryTreeSize(BTNode* root);
 
void BinaryTreeSize2(BTNode* root);
 
//统计二叉树的叶子节点个数
int BinaryTreeleaf(BTNode* root);
 
//计算二叉树的高度层次
int BinaryTreeHigh(BTNode* root);
 
//计算二叉树的第K层的节点树
int BinaryTreeKlevel(BTNode* root,int k);
 
//查找二叉树某个节点的值
BTNode* TreeFind(BTNode* root, BTDataType x);

.c文件：


#include"Binary Tree.h"
#define _CRT_SECURE_NO_WARNINGS 1
 
//创建二叉树
BTNode* TreeCreate() {
	BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
	assert(n1);
	BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
	assert(n2);
	BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
	assert(n3);
	BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
	assert(n4);
	BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
	assert(n5);
	BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
	assert(n6);
	BTNode* n7 = (BTNode*)malloc(sizeof(BTNode));
	assert(n7);
 
	n1->data = 1;
	n2->data = 2;
	n3->data = 3;
	n4->data = 4;
	n5->data = 5;
	n6->data = 6;
	n7->data = 7;
 
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n2->right = NULL;
	n3->left = NULL;
	n3->right = n7;
	n7->left= NULL;
	n7->right = NULL;
	n4->left = n5;
	n4->right = n6;
	n5->left = NULL;
	n5->right =NULL;
	n6->left = NULL;
	n6->right = NULL;
 
	return n1;
 
}
 
//二叉树的前序遍历
void PreOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历根
	printf("%d  ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
 
//二叉树的中序遍历
void InOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历左子树，再根，再右
	InOrder(root->left);
	printf("%d  ", root->data);
	InOrder(root->right);
}
 
//二叉树的后序遍历
void PostOrder(BTNode* root) {
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	//先遍历左子树，再右，最后根
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d  ", root->data);
}
 
//统计二叉树的所有节点个数——分而治之（大事化小，小事化了）
int BinaryTreeSize(BTNode* root) {
	return root == NULL ? 0 : 
		BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
 
//统计二叉树的所有节点个数—-错误写法
static int count = 0;
void  BinaryTreeSize2(BTNode* root) {
	if (root == NULL)
		return ;
	++count;
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
 
}
 
 
 
//统计二叉树的叶子节点个数
int BinaryTreeleaf(BTNode* root) {
	if (root == NULL) {
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
		return 1;
 
	return BinaryTreeleaf(root->left) + BinaryTreeleaf(root->right);
}
 
//计算二叉树的高度层次
int BinaryTreeHigh(BTNode* root) {
	if (root == NULL)
		return 0;
	int leftHigh = BinaryTreeHigh(root->left);
	int rightHigh = BinaryTreeHigh(root->right);
	return leftHigh > rightHigh ? leftHigh + 1 : rightHigh + 1;
}
 
 
//计算二叉树的第K层的节点数
int BinaryTreeKlevel(BTNode* root,int k) {
	assert(k > 0);
	if (root == NULL) {	//表明该层无节点
		return 0;
	}
	if (k == 1)		//表明在第一层
		return 1;
 
	//求二叉树的第K层节点就是求它的左右子树的第K-1层节点相加所得
	return BinaryTreeKlevel(root->left, k - 1) +
		BinaryTreeKlevel(root->right, k - 1);
}
 
 
//查找二叉树某个节点的值
BTNode* TreeFind(BTNode* root, BTDataType x) {
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	//先从左子树开始
	BTNode* lret = TreeFind(root->left, x);
	if (lret)
		return lret;
 
	//找不到后再从右子树开始
	BTNode* rret = TreeFind(root->right, x);
	if (rret)
		return rret;
	//两边都找不到后，返回空
	return NULL;
}
 
//销毁二叉树——使用后序遍历，先消除左右子树，最后消除跟节点（从下到上）
void TreeDestory(BTNode* root) {
	if (root == NULL) {
		return;
	}
	TreeDestory(root->left);
	TreeDestory(root->right);
	free(root);
	root == NULL;
}
 
 
//主函数
int main() {
	BTNode* root = TreeCreate();
	/*printf("前序遍历：");
	PreOrder(root);
	printf("\n");*/
 
	//printf("中序遍历：");
	//InOrder(root);
	//printf("\n");
 
	/*printf("后序遍历：");
	PostOrder(root);
	printf("\n");*/
 
 
	printf("TreeSize:%d \n", BinaryTreeSize(root));
	printf("TreeSize:%d \n", BinaryTreeSize(root));
 
 
	计算节点个数的错误写法
	///*printf("节点个数：%d \n", count);
	//printf("节点个数：%d \n", count);*/
 
 
	printf("TreeLeaf:%d \n", BinaryTreeleaf(root));
 
	printf("TreeHigh:%d \n", BinaryTreeHigh(root));
 
    printf("Tree K level:%d \n", BinaryTreeKlevel(root, 1));
	printf("Tree K level:%d \n", BinaryTreeKlevel(root, 2));
	printf("Tree K level:%d \n", BinaryTreeKlevel(root, 3));
	printf("Tree K level:%d \n", BinaryTreeKlevel(root, 4));
 
	printf("\n");
	BTNode* ret = TreeFind(root, 3);
	if (ret)
		printf("该节点存在，且地址值为：%p\n", ret);
	else
	printf("该节点在二叉树中不存在！\n");
 
	return 0;
}

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/笔触狂放9/article/detail/727105

链式二叉树的代码实现_二叉树链式存储结构代码

目录

二叉树的存储结构：

链式二叉树的实现

1.二叉树的结构体类型

2.创建二叉树结点

代码实现：

3.二叉树的前序遍历

测试结果：

4.二叉树的中序遍历

测试结果：

5.二叉树的后序遍历

测试结果：

6.求二叉树的总结点个数

错误写法：

所以正确的代码实现：

测试结果：

7.求二叉树的叶子节点个数

测试结果：

8.求二叉树的高度层次

测试结果：

9.求二叉树第K层的节点个数

测试结果：

10.查找二叉树某个节点的值

测试结果：

11.二叉树的销毁

完整的链式二叉树代码：

.h文件：

.c文件：