西瓜书研读——第四章 决策树：ID3、C4.2、CSRT算法_id3算法西瓜决策树

西瓜书研读系列：
西瓜书研读——第三章 线性模型：一元线性回归

西瓜书研读——第三章 线性模型：多元线性回归

西瓜书研读——第三章 线性模型：线性几率回归（逻辑回归）

西瓜书研读——第三章 线性模型： 线性判别分析 LDA

• 主要教材为西瓜书，结合南瓜书，统计学习方法，B站视频整理~
• 人群定位：学过高数会求偏导、线代会矩阵运算、概率论知道啥是概率
• 原理讲解，公式推导，课后习题，实践代码应有尽有，欢迎订阅

4 决策树

决策树（Decision Tree）是一种非参数的有监督学习方法，它能够从一系列有特征和标签的数据中总结出决策规则，并用树状图的结构来呈现这些规则，以解决分类和回归问题，决策树算法的本质是一种图结构。

决策树算法容易理解，适用各种数据，在解决各种问题时都有良好表现，尤其是以树模型为核心的各种集成算法，在各个行业和领域都有广泛的应用。

4.1 基本概念与构造流程

以西瓜数据集为例，决策树是如何生成的？

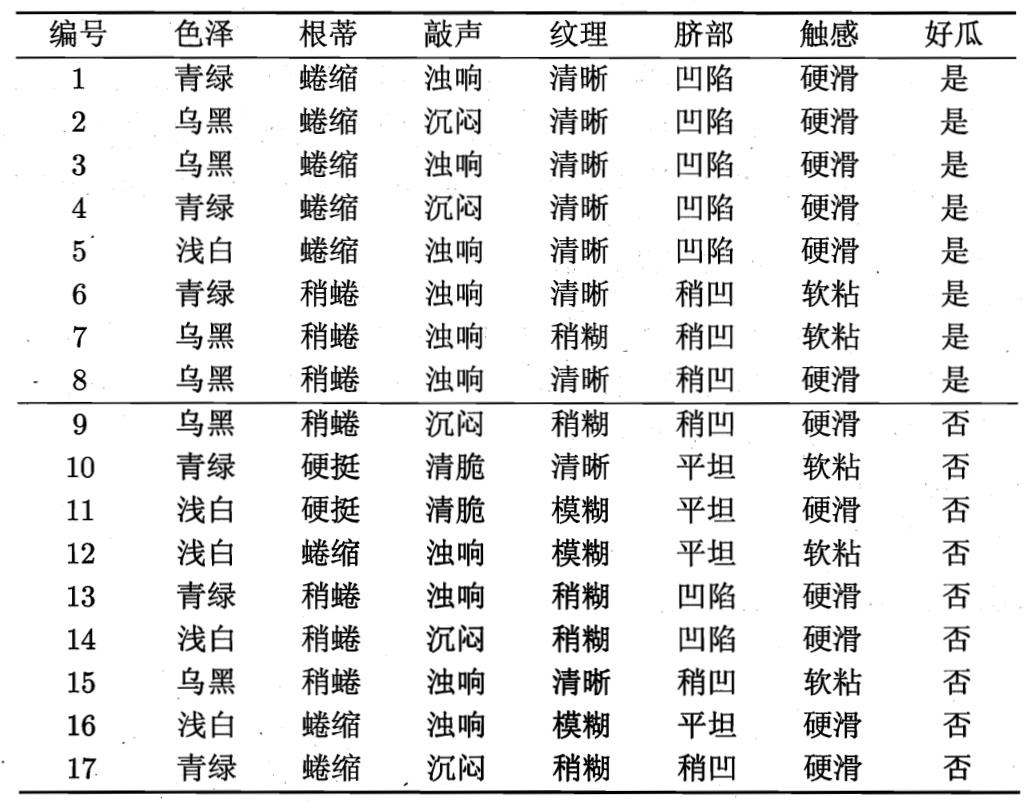
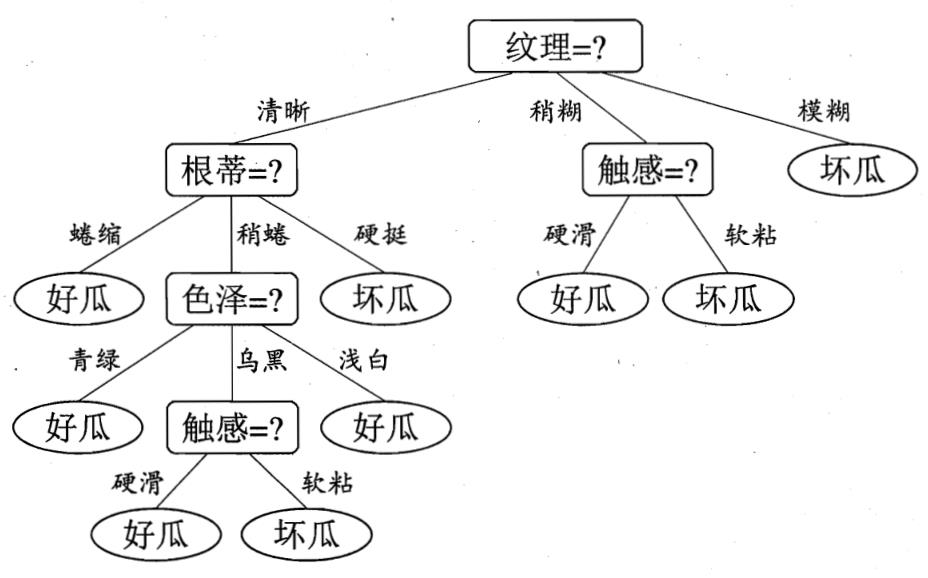
在上图的决策树中，决策过程的每一次判定都是对某一属性的“测试”，决策最终结论则对应最终的判定结果。一般一棵决策树包含：一个根节点、若干个内部节点和若干个叶子节点，易知：

• 非叶节点：表示一个特征属性测试。
• 分支：代表这个特征属性在某个值域上的输出。
• 叶子节点：存放一个类别。

每个结点包含的样本集合根据属性测试的结果被划分到子结点中，而根结点包含了样本全集。
从根结点到每个叶结点的路径对应了一个判定测试序列

构造流程

决策树的生成是一个递归过程

三种会导致递归返回的情形

• 当前结点包含的样本全属于同一类别，无需划分
• 当前属性集为空，或是所有样本在所有属性上取值相同，无法划分
  • 把当前结点标记为叶结点，并将其类别设定为该结点所含样本最多的类别
  • 利用当前结点的后验分布
• 当前结点包含的样本集合为空，不能划分
  • 把当前结点标记为叶结点，但将其类别设定为父结点所含样本做多的类别
  • 把父结点的样本分布作为当前结点的先验分布

决策树各类算法的核心就就在于：如何解决“从A中选择最优划分属性”？

4.2 划分选择

核心问题：如何解决“从A中选择最优划分属性”？

划分目的：决策树分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”（purity）越来越高

---

点击查看信息论补充知识

信息熵（information entropy）

在决策树种，信息熵通常是用来度量样本集合纯度最常用的一种指标，信息量越大 信息熵越大，不确定性越大。
$$\mathrm{Ent}(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k$$
条件熵：表示的是在已知一个随机变量的条件下，另一个随机变量的不确定性。

具体地，假设有随机变量$X$和$Y$，且它们服从以下联合概率分布
$$P(X=x_i,Y=y_j)=p_{ij}i=1,2,....,n;j=1,2,...,m$$
那么在已知$X$的条件下，随机变量$Y$的条件熵为
$$H(Y|X)=\sum _{x}p(x)H(Y|X=x)$$

$$\mathrm{Ent}(Y|X)=\sum _{i=1}^n{p}_i\mathrm{Ent}(Y|X=x_i)$$

其中，$ p_i = P(X = x_i) ，i =1,2,…,n$。

在信息论中信息增益也称为互信息

互信息:信息熵和条件熵的差，它表示的是已知一个随机变量的信息后使得另一个随机变量的不确定性减少的程度。

具体地，假设有随机变量$X$和$Y$，那么在已知$X$的信息后，$Y$的不确定性减少的程度为
$$I(Y;X)=\mathrm{Ent}(Y)-\mathrm{Ent}(Y|X)$$
此即为互信息的数学定义。

---

证明$0\le \mathrm{Ent}(D)\le {\log }_2|\mathcal{Y}|$：

已知集合$D$的信息熵的定义为
$$\mathrm{Ent}(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k$$
其中，$|\mathcal{Y}|$表示样本类别总数，$p_k$表示第$k$类样本所占的比例，且$0\le p_k\le 1,{\sum }_{k=1}^n{p}_k=1$。若令$|\mathcal{Y}|=n,p_k=x_k$，那么信息熵$\mathrm{Ent}(D)$就可以看作一个$n$元实值函数，也即
$$\mathrm{Ent}(D)=f(x_1,...,x_n)=-\sum _{k=1}^n{x}_k{\log }_2{x}_k$$
其中，$0\le x_k\le 1,{\sum }_{k=1}^n{x}_k=1$，下面考虑求该多元函数的最值。首先我们先来求最大值，如果不考虑约束$0\le x_k\le 1$，仅考虑${\sum }_{k=1}^n{x}_k=1$的话，对$f(x_1,...,x_n)$求最大值等价于如下最小化问题
min ⁡ ∑ k = 1 n x k log ⁡ 2 x k  s.t.  ∑ k = 1 n x k = 1

$$\begin{array}{ll}{ \operatorname{min}} & {\sum\limits_{k=1}^{n} x_{k} \log _{2} x_{k} } \\ {\text { s.t. }} & {\sum\limits_{k=1}^{n}x_k=1} \end{array}$$ min s.t. ​k=1∑n​xk​log2​xk​k=1∑n​xk​=1​
显然，在$0\le x_k\le 1$时，此问题为凸优化问题，而对于凸优化问题来说，能令其拉格朗日函数的一阶偏导数等于0的点即为最优解。根据拉格朗日乘子法可知，该优化问题的拉格朗日函数为
$$L(x_1,...,x_n,\lambda )=\sum _{k=1}^n{x}_k{\log }_2{x}_k+\lambda (\sum _{k=1}^n{x}_k-1)$$
其中，$\lambda$为拉格朗日乘子。对$L(x_1,...,x_n,\lambda )$分别关于$x_1,...,x_n,\lambda$求一阶偏导数，并令偏导数等于0可得
$$\begin{array}{rl}\frac{\partial L(x_1,...,x_n,\lambda )}{\partial x_1}& =\frac{\partial }{\partial x_1}\left[\sum _{k=1}^n{x}_k{\log }_2{x}_k+\lambda (\sum _{k=1}^n{x}_k-1)\right]=0\\ & ={\log }_2{x}_1+x_1\cdot \frac{1}{x_1\ln 2}+\lambda =0\\ & ={\log }_2{x}_1+\frac{1}{\ln 2}+\lambda =0\\ & \Rightarrow \lambda =-{\log }_2{x}_1-\frac{1}{\ln 2}\\ \frac{\partial L(x_1,...,x_n,\lambda )}{\partial x_2}& =\frac{\partial }{\partial x_2}\left[\sum _{k=1}^n{x}_k{\log }_2{x}_k+\lambda (\sum _{k=1}^n{x}_k-1)\right]=0\\ & \Rightarrow \lambda =-{\log }_2{x}_2-\frac{1}{\ln 2}\\ ⋮& \\ \frac{\partial L(x_1,...,x_n,\lambda )}{\partial x_n}& =\frac{\partial }{\partial x_n}\left[\sum _{k=1}^n{x}_k{\log }_2{x}_k+\lambda (\sum _{k=1}^n{x}_k-1)\right]=0\\ & \Rightarrow \lambda =-{\log }_2{x}_n-\frac{1}{\ln 2}\\ \frac{\partial L(x_1,...,x_n,\lambda )}{\partial \lambda }& =\frac{\partial }{\partial \lambda }\left[\sum _{k=1}^n{x}_k{\log }_2{x}_k+\lambda (\sum _{k=1}^n{x}_k-1)\right]=0\\ & \Rightarrow \sum _{k=1}^n{x}_k=1\end{array}$$
整理一下可得
$$\{\begin{array}{l}\lambda =-{\log }_2{x}_1-\frac{1}{\ln 2}=-{\log }_2{x}_2-\frac{1}{\ln 2}=...=-{\log }_2{x}_n-\frac{1}{\ln 2}\\ \sum _{k=1}^n{x}_k=1\end{array}$$
由以上两个方程可以解得
$$x_1=x_2=...=x_n=\frac{1}{n}$$
又因为$x_k$还需满足约束$0\le x_k\le 1$，显然$0\le \frac{1}{n}\le 1$，所以$x_1=x_2=...=x_n=\frac{1}{n}$是满足所有约束的最优解，也即为当前最小化问题的最小值点，同时也是$f(x_1,...,x_n)$的最大值点。将$x_1=x_2=...=x_n=\frac{1}{n}$代入$f(x_1,...,x_n)$中可得
$$f(\frac{1}{n},...,\frac{1}{n})=-\sum _{k=1}^n\frac{1}{n}{\log }_2\frac{1}{n}=-n\cdot \frac{1}{n}{\log }_2\frac{1}{n}={\log }_{2}n$$
所以显然$f(x_1,...,x_n)$在满足约束$0\le x_k\le 1,{\sum }_{k=1}^n{x}_k=1$时的最大值为${\log }_{2}n$。

求完最大值后下面我们再来求最小值，如果不考虑约束${\sum }_{k=1}^n{x}_k=1$，仅考虑$0\le x_k\le 1$的话，$f(x_1,...,x_n)$可以看做是$n$个互不相关的一元函数的加和，也即
$$f(x_1,...,x_n)=\sum _{k=1}^{n}g(x_k)$$
其中，$g(x_k)=-x_k{\log }_2{x}_k,0\le x_k\le 1$。那么当$g(x_1),g(x_2),...,g(x_n)$分别取到其最小值时，$f(x_1,...,x_n)$也就取到了最小值。所以接下来考虑分别求$g(x_1),g(x_2),...,g(x_n)$

各自的最小值，由于$g(x_1),g(x_2),...,g(x_n)$的定义域和函数表达式均相同，所以只需求出$g(x_1)$的最小值也就求出了$g(x_2),...,g(x_n)$的最小值。下面考虑求$g(x_1)$的最小值，首先对$g(x_1)$关于$x_1$求一阶和二阶导数

$$g^{\prime }(x_1)=\frac{d(-x_1{\log }_2{x}_1)}{d{x}_1}=-{\log }_2{x}_1-x_1\cdot \frac{1}{x_1\ln 2}=-{\log }_2{x}_1-\frac{1}{\ln 2}$$

$$g^{\prime \prime }(x_1)=\frac{d\left(g^{\prime }(x_1)\right)}{d{x}_1}=\frac{d\left(-{\log }_2{x}_1-\frac{1}{\ln 2}\right)}{d{x}_1}=-\frac{1}{x_1\ln 2}$$
显然，当$0\le x_k\le 1$时$g^{\prime \prime }(x_1)=-\frac{1}{x_1\ln 2}$恒小于0，所以$g(x_1)$是一个在其定义域范围内开口向下的凹函数，那么其最小值必然在边界取，于是分别取$x_1=0$和$x_1=1$，代入$g(x_1)$可得
$$\begin{gathered} g(0)=-0{\log }_{2}0=0 \\ g(1)=-1{\log }_{2}1=0 \end{gathered}$$
所以，$g(x_1)$的最小值为0，同理可得$g(x_2),...,g(x_n)$的最小值也为0，那么$f(x_1,...,x_n)$的最小值此时也为0。

综上可知，当$f(x_1,...,x_n)$取到最大值时：$x_1=x_2=...=x_n=\frac{1}{n}$，此时样本集合纯度最低；当$f(x_1,...,x_n)$取到最小值时：$x_k=1,x_1=x_2=...=x_{k-1}=x_{k+1}=...=x_n=0$，此时样本集合纯度最高。

• $\text{Ent}(D)$ 的值越小，则 $D$ 的纯度越高
• $\text{Ent}(D)$ 的最小值为0，最大值为 ${\log }_2|\mathcal{Y}|$

---

4.2.1 信息增益 （ ID3算法）

一般而言，信息增益越大，即取值后样本集的不确定性减小的程度越大，则意味着使用属性