- 1计算机网络 - UDP/TCP、IP、MAC报文协议格式_mac数据包的格式
- 2ThinkPHP+Redis实现简单抽奖_thinkphp随机抽题
- 3如何使用机器学习构建自己的推荐系统?
- 4OpenAI王炸模型引爆科技圈,官方技术报告说了什么?
- 5利用Amazon Mobile Analytics与R深入探究移动应用的使用模式_aws mobile analytics
- 6鸿蒙电视哔哩哔哩,[4K视频] 65寸智能电视只要3299元?荣耀智慧屏X1开箱
- 7Android夜间模式DayNight问题_error: resource style/theme.material3.daynight.noa
- 8python 操作Excel(5)pandas之自定义排序_pandas中自定义排序
- 9编码器-解码器(seq2seq)_编码器解码器模型
- 10关于extern “C“ {} 的理解_extern "c" {
卡尔曼滤波的五大公式及python代码示例_卡尔曼滤波器五个公式
赞
踩
一、系统的状态方程
状态方程是根据上一时刻的状态和控制变量来推测此刻的状态
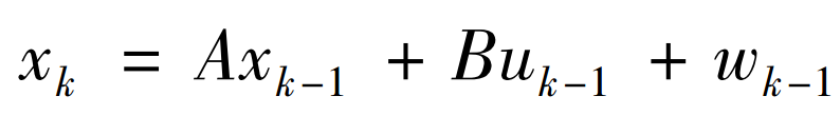
- x k x_{k} xk 是状态分量的 n n n维矢量
- A A A 是 n ∗ n n * n n∗n 的状态转移矩阵,也就是对目标状态转换的猜想模型,是已知的
- u k − 1 u_{k-1} uk−1 是新的,让系统可以接受外部控制
- B B B 是 n ∗ c n * c n∗c 矩阵,将输入转换为状态的矩阵
- w k − 1 w_{k-1} wk−1 是预测过程的噪声,对应 x k x_{k} xk中每个分量的噪声,期望为0,协方差为 Q Q Q的高斯白噪声
二、观测方程
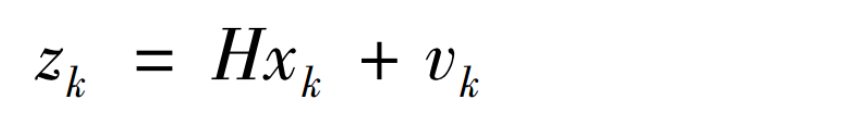
- H H H 是 m ∗ n m * n m∗n矩阵,是状态变量(观测)的转换矩阵,表示将状态和观测连接起来的关系,卡尔曼滤波里为线性关系,它负责将 m 维的测量值转换到 n 维,使之符合状态变量的数学形式,是滤波的前提条件之一。
- v k v_{k} vk 观测噪声,服从高斯分布 N ( 0 , R ) N(0, R) N(0,R) , R R R 即下文测量噪声
三、五大公式
以下摘自
卡尔曼滤波五个公式各个参数的意义
- 信息过程足够精确的模型,是由白噪声所激发的线性(也可以是时变)的动态系统
- 每次测量的信号都包含这附加的白噪声分量
当满足以上假设时,可以应用卡尔曼滤波算法
卡尔曼滤波算法有两个基本假设:
卡尔曼滤波算法分为两步:预测和更新
- 预测 : 根据上一时刻( k - 1 k - 1 k-1 时刻) 的后验估计值来估计当前时刻( k k k 时刻) 的状态,得到 k k k 时刻的先验估计值;
- 更新: 使用当前时刻的测量值来更正预测阶段估计值,得到当前时刻的后验估计值。
卡尔曼滤波器可以分为时间更新方程和测量更新方程。时间更新方程(即预测阶段)根据前一时刻的状态估计值推算当前时刻的状态变量先验估计值和误差协方差先验估计值; 测量更新方程(即更新阶段)负责将先验估计和新的测量变量结合起来构造改进的后验估计。时间更新方程和测量更新方程也被称为预测方程和校正方程。因此卡尔曼算法是一个递归的预测—校正方法。

-
1,
 : 分别表示 k - 1 时刻和 k 时刻的后验状态估计值,是滤波的结果之一,即更新后的结果,也叫最优估计(估计的状态,根据理论,我们不可能知道每时刻状态的确切结果所以叫估计)。
: 分别表示 k - 1 时刻和 k 时刻的后验状态估计值,是滤波的结果之一,即更新后的结果,也叫最优估计(估计的状态,根据理论,我们不可能知道每时刻状态的确切结果所以叫估计)。 -
2,
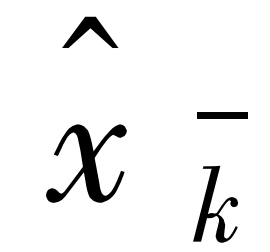 : k 时刻的先验状态估计值,是滤波的中间计算结果,即根据上一时刻(k-1时刻)的最优估计预测的k时刻的结果,是预测方程的结果。
: k 时刻的先验状态估计值,是滤波的中间计算结果,即根据上一时刻(k-1时刻)的最优估计预测的k时刻的结果,是预测方程的结果。 -
3,
 :分别表示 k - 1 时刻和 k 时刻的后验估计协方差(即
:分别表示 k - 1 时刻和 k 时刻的后验估计协方差(即 的协方差,表示状态的不确定度),是滤波的结果之一。
的协方差,表示状态的不确定度),是滤波的结果之一。 -
4,
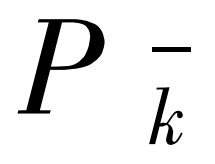 :k 时刻的先验估计协方差(
:k 时刻的先验估计协方差(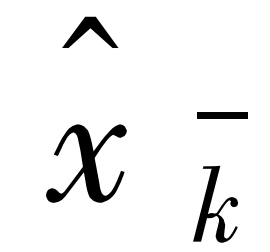 的协方差),是滤波的中间计算结果。
的协方差),是滤波的中间计算结果。 -
5,
 :是状态变量到测量(观测)的转换矩阵,表示将状态和观测连接起来的关系,卡尔曼滤波里为线性关系,它负责将 m 维的测量值转换到 n 维,使之符合状态变量的数学形式,是滤波的前提条件之一。
:是状态变量到测量(观测)的转换矩阵,表示将状态和观测连接起来的关系,卡尔曼滤波里为线性关系,它负责将 m 维的测量值转换到 n 维,使之符合状态变量的数学形式,是滤波的前提条件之一。 -
6,
 :测量值(观测值),是滤波的输入。
:测量值(观测值),是滤波的输入。 -
7,
 :滤波增益矩阵,是滤波的中间计算结果,卡尔曼增益,或卡尔曼系数。
:滤波增益矩阵,是滤波的中间计算结果,卡尔曼增益,或卡尔曼系数。 -
8,
 :状态转移矩阵,实际上是对目标状态转换的一种猜想模型。例如在机动目标跟踪中, 状态转移矩阵常常用来对目标的运动建模,其模型可能为匀速直线运动或者匀加速运动。当状态转移矩阵不符合目标的状态转换模型时,滤波会很快发散。
:状态转移矩阵,实际上是对目标状态转换的一种猜想模型。例如在机动目标跟踪中, 状态转移矩阵常常用来对目标的运动建模,其模型可能为匀速直线运动或者匀加速运动。当状态转移矩阵不符合目标的状态转换模型时,滤波会很快发散。 -
9,Q:过程激励噪声协方差(系统过程的协方差)。该参数被用来表示状态转换矩阵与实际过程之间的误差。因为我们无法直接观测到过程信号, 所以 Q 的取值是很难确定的。是卡尔曼滤波器用于估计离散时间过程的状态变量,也叫预测模型本身带来的噪声。状态转移协方差矩阵
-
10:R: 测量噪声协方差。滤波器实际实现时,测量噪声协方差 R一般可以观测得到,是滤波器的已知条件。
-
11,B:是将输入转换为状态的矩阵
四、Python代码
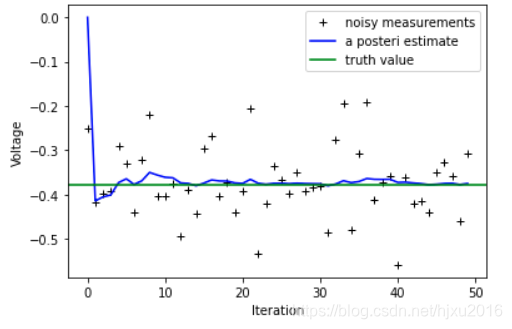
这里真实值为 x=-0.377,且假设A=1, H=1
观测值存在噪声,那么如何估计出实际的值呢?
这里给出两种方案,一种是北卡大学开源的,直接通过公式计算的结果
# -*- coding=utf-8 -*-
# Kalman filter example demo in Python
# A Python implementation of the example given in pages 11-15 of "An
# Introduction to the Kalman Filter" by Greg Welch and Gary Bishop,
# University of North Carolina at Chapel Hill, Department of Computer
# Science, TR 95-041,
# http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html
# by Andrew D. Straw
#coding:utf-8
import numpy
import pylab
#这里是假设A=1,H=1的情况
# 参数初始化
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # 真实值
z = numpy.random.normal(x,0.1,size=sz) # 观测值 ,观测时存在噪声
Q = 1e-5 # process variance
# 分配数组空间
xhat=numpy.zeros(sz) # x 滤波估计值
P=numpy.zeros(sz) # 滤波估计协方差矩阵
xhatminus=numpy.zeros(sz) # x 估计值
Pminus=numpy.zeros(sz) # 估计协方差矩阵
K=numpy.zeros(sz) # 卡尔曼增益
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# 预测
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# 更新
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
pylab.figure()
pylab.plot(z,'k+',label='noisy measurements') #观测值
pylab.plot(xhat,'b-',label='a posteri estimate') #滤波估计值
pylab.axhline(x,color='g',label='truth value') #真实值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
pylab.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
另外一种是调用from filterpy.kalman里的卡尔曼滤波函数
from filterpy.kalman import KalmanFilter
import numpy as np
np.random.seed(0)
kf = KalmanFilter(dim_x=1, dim_z=1)
kf.F = np.array([1])
kf.H = np.array([1])
kf.R = np.array([0.1**2])
kf.P = np.array([1.0])
kf.Q = 1e-5
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
kf.predict()
xhat[k] = kf.x
kf.update(z[k], 0.1**2, np.array([1]))
pylab.figure()
pylab.plot(z,'k+',label='noisy measurements') #观测值
pylab.plot(xhat,'b-',label='a posteri estimate') #滤波估计值
pylab.axhline(x,color='g',label='truth value') #真实值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
pylab.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
python-opencv中的卡尔曼滤波函数
kalman = cv2.KalmanFilter(1, 1)
kalman.transitionMatrix = np.array([[1]], np.float32) # 转移矩阵 A
kalman.measurementMatrix = np.array([[1]], np.float32) # 测量矩阵 H
kalman.measurementNoiseCov = np.array([[1]], np.float32) * 0.01 # 测量噪声 R
kalman.processNoiseCov = np.array([[1]], np.float32) * 1e-5 # 过程噪声 Q
kalman.errorCovPost = np.array([[1.0]], np.float32) # 最小均方误差 P
xhat = np.zeros(sz) # x 滤波估计值
kalman.statePost = np.array([xhat[0]], np.float32)
for k in range(1, n_iter):
# print(np.array([z[k]], np.float32))
mes = np.reshape(np.array([z[k]], np.float32), (1, 1))
# # print(mes.shape)
xhat[k] = kalman.predict()
kalman.correct(np.array(mes, np.float32))
pylab.figure()
pylab.plot(z, 'k+', label='noisy measurements') # 观测值
pylab.plot(xhat, 'b-', label='a posteri estimate') # 滤波估计值
pylab.axhline(x, color='g', label='truth value') # 真实值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
pylab.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
三者都能得到同一结果