R语言-生存分析（K-M曲线、森林图、列线图）_队列研究中的森林图

生存分析定义

随访研究（follow-up study）是一种前瞻性研究（prospective study）
随访研究的研究设计可以是横断面研究（cross sectional study）、病例对照研究（case-control study），也可以是队列研究（cohort study）。

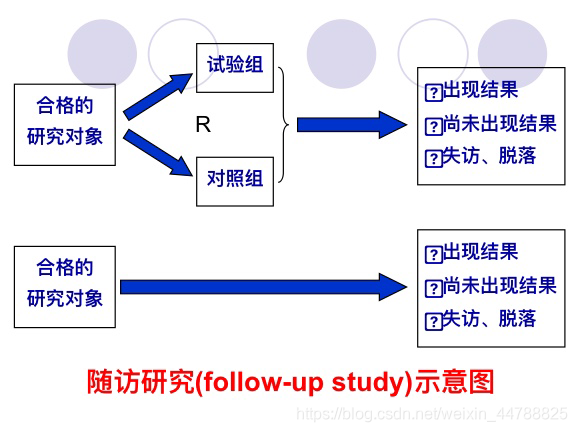
　　这类研究的应用情景就是：我们关注的临床结局是一个事件，比如：死亡，复发，症状消失，疾病痊愈等等，且在很多情况下，我们不仅关注事件是否发生，还会关注事件发生的早晚，以及，由于研究周期的限定，和患者依从性等的差异，我们不可能追踪到所有结局事件的发生。针对这种情景收集到的数据，我们使用的描述分析方法就是生存分析。生存的意义很广泛，它可以指人或动物的存活（相对于死亡),可以是患者的病情正处于缓解状态（相对于再次复发或恶化），还可以是某个系统或产品正常工作（相对于失效或故障），甚至可是是客户的流失与否等。
　　
　　在生存分析中，研究的主要对象是寿命超过某一时间的概率。还可以描述其他一些事情发生的概率，例如产品的失效、出狱犯人第一次犯罪、失业人员第一次找到工作等等。在某些领域的分析中，常常用追踪的方式来研究事物的发展规律，比如研究某种药物的疗效，手术后的存活时间，某件机器的使用寿命等。
　　
　　生存分析对一个或多个非负随机变量进行统计推断，研究生存现象和响应时间数据及其统计规律，是一种既考虑结果又考虑生存时间的一种统计方法，并可充分利用截尾数据所提供的不完全信息，对生存时间的分布特征进行描述，对影响生存时间的主要因素进行分析。生存分析不同于其它多因素分析的主要区别点：生存分析考虑了每个观测出现某一结局的时间长短。
　　生存分析的目的主要包括估计、比较、影响因素分析和预测：
估计：根据样本生存资料估计总体生存率及其它有关指标 （ 如中位生存期等 ） ， 如根据脑瘤患者治疗后的生存时间资料 ， 估计不同时间的生存率 、生存曲线以及中位生存期等 。
比较 ：对不同处理组生存率进行比较，如比较不同疗法治疗脑瘤的生存率，以了解哪种治疗方案较优。
影响因素分析 ：目的是为了探索和了解影响生存时间长短的因素 ， 或平衡某些因素影响后 ， 研究某个或某些因素对生存率的影响 。 如为改善脑瘤病人的预后 ， 应了解影响病人预后的主要因素 ， 包括病人的年龄 、 性别 、 病程 、 肿瘤分期 、 治疗方案等 。
预测 ：具有不同因素水平的个体生存预测 ，如根据脑瘤病人的年龄 、 性别 、 病程 、 肿瘤分期 、 治疗方案等预测该病人t 年（ 月 ）生存率 。

生存分析的研究内容

1.描述生存过程
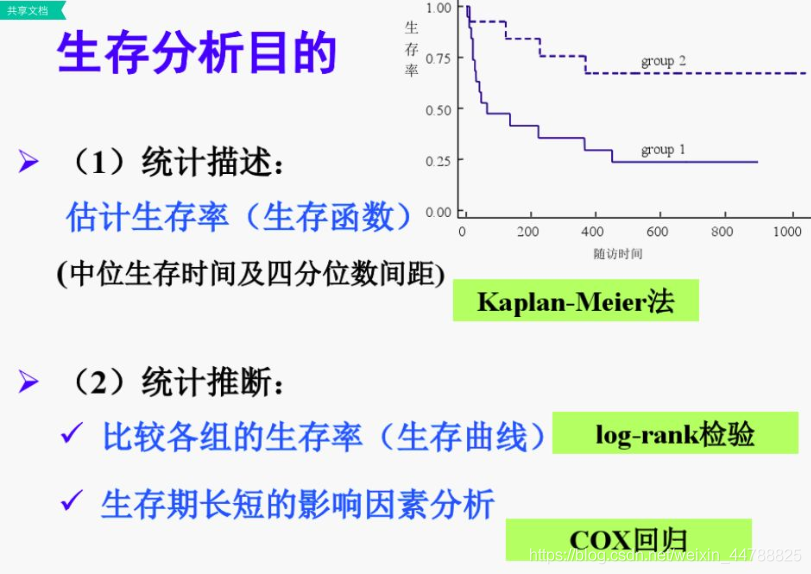
　　研究生存时间的分布特点，估计生存率及平均存活时间，绘制生存曲线等，根据生存时间的长短，可以估算出各个时点的生存率，并根据生存率来估计中位生存时间，也可以根据生存曲线分析其生存特点，一般使用Kaplan-Meier法和寿命表法。
2.比较生存过程
　　可通过生存率及其标准误对各样本的生存率进行比较，以探讨各组间的生存过程是否存在差异，对过程的检验包括：非参数检验、参数检验和半参数检验。
3.分析危险因素
　　是通过生存分析参数、半参数模型来探讨影响生存时间和终点事件的保护因素和不利因素，因素作用的大小及方向，相对危险度的大小，基本使用半参数Cox回归模型。

生存分析资料的特点

资料要求
1.样本由随机抽样方法获得，要有一定的数量，死亡例数和比例不能太少
2.完整数据所占的比例不能太少，即截尾值不宜太多，一般截尾少于20%
3.截尾值出现的原因无偏性，为防止偏性常常对被截尾的研究对象的年龄、职业、地区、病情轻重等情况进行分析
4.生存时间尽可能精确
5.缺项要尽量补齐

生存资料的共同特点
1.蕴含有结局和时间两个方面的信息
2.结局为两分类互斥事件
3一般是通过随访收集得到，随访观察往往是从某统一时间点(如入院或实施手术等某种处理措施后)开始，观察到某规定时间点截止。
4.常因失访等原因造成研究对象的生存时间数据不完整，分布类型复杂，不能简中地套用以前的多因素分析方法

生存资料的基本名词概念

生存时间：终点事件与起始事件之间的时间间隔。终点事件指研究者所关心的特定结局；起始事件是起始特征的事件。终点事件和起始事件是相对而言的，都是由研究目的决定的，在研究之初明确规定，在研究期间严格遵守。
　　完全数据：生存时间的数据是完全的，指观察对象在观察期内出现终点事件，纪律到的时间信息是完整的。
　　截尾数据：尚未观察到研究对象出现终点事件时，由于某种原因停止了随访，这时记录到的时间信息是不完整的，这种生存时间数据称为不完全数据或截尾值。常用符号“+”表示。截尾的主要原因有三种：①失访（lost of follow up）中途失访，包括拒绝访问、失去联系等。②退出（quit of experiment），中途退出试验、改变治疗方案，死于其他与研究无关的因素：如肺癌患者死于心肌梗死，自杀或者因车祸死亡。③终止（terminated），指观察期结束仍未出现结局。
条件死亡概率：表示某时段开始存活的个体，在该时段内死亡的可能性，如年死亡概率q=某年内死亡人数/某年年初人口数，如果年内存在删失数据，需要对分母进行校正，校正人口数=年初人口数-删失例数/2。
条件生存概率：某时段开始时存活的个体，到该时段结束时让然存活的可能性p=某年存活满一年的人数/某年年初人口数=1-q，如果年内存在删失数据，需要对分母进行校正，校正人口数=年初人口数-删失例数/2。
生存率(survival rate)：又称生存概率和生存函数，他表示一个病人的生存时间长于时间t的概率，用S(t)表示，S(t) = P(T ≥ t)。
死亡率：又称死亡概率和死亡函数，他表示一个病人的生存时间小于时间t的概率，用F(t)表示，F(t) = P(T ≤ t)，F(t) = 1 - S(t)。
生存曲线(survival curve)：以时间为横坐标，S(t)为纵坐标所做的曲线称为生存率曲线，他是一条下降的曲线，下降的坡度越陡，表示生存率越低或生存时间越短，其斜率表示死亡速率。
中位生存时间(median survival time)：又称半数生存期，表示恰好有50 ％的个体尚存活的时间。中位生存期越长，表示疾病的预后越好；中位生存期越短，预后越差。估计中位生存期常用图解法或线性内插法，注意与生存时间中位数区分。
死亡密度函数(death density function)：是死亡函数F(t)的导数，表示观察对象在t时刻的瞬时死亡率，记作f(t)。
累积风险函数：指某时点之后的累积死亡风险，用H(t)表示。
风险函数(hazard function)：是单位时间死亡的的概率，用h(t)表示，是H(t)的导数。风险函数是生存分析的基本函数，他反映研究对象在某时点的死亡风险的大小。h(t) = (死于区间(t , t + ▲t)的病人数) / (在t时刻尚存的病人数)。

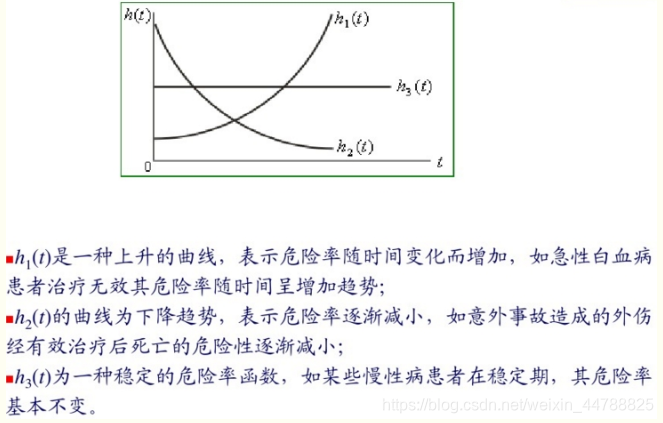
风险比(hazard ratio)：约等于相对危险度(relative risk)，即两组的风险函数之比。
　　
　　生存函数、风险函数和累积风险函数在数学上是等价的，但在分析的意义上缺不等价。风险函数的估计容易受随机误差的影响，而生存函数则相对稳定。
　　
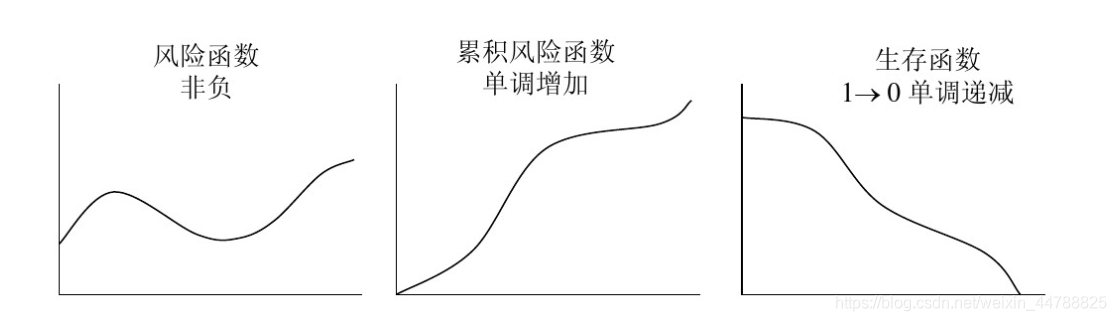
　　在数学上，上面的几种函数都是可以相互推算出来的：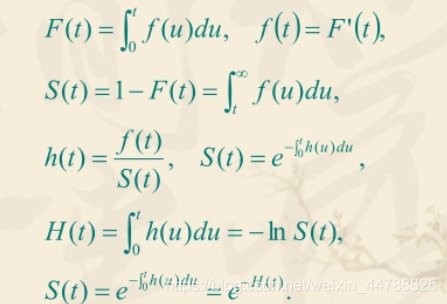

R语言+生存分析

一、生存过程描述

当我们要描述生存分析数据时，我们常常使用生存曲线来展示，这个时候需要估计每个时间点的生存率，用的就是K-M方法。因此准确来说，K-M方法是一种统计描述方法，就好比用饼图来展示比例，用箱型图来表示连续变量。
相比较于寿命表法（life table method)，K-M方法更加充分的利用了信息，给出了更加准确的统计量，寿命表的绘制只要是知道了公式，在excel中绘制也是非常方便的，所以在这里就不涉及了。同时，作为一种非参数统计方法，不要求总体的分布形式，因此非常适合生存分析资料。K-M曲线还可以很直观的表现出两组或多组的生存率和死亡率，也非常适合在文章中展示。

K-M曲线的绘制：
需要使用‘survival’和‘survminer’包，分别做数据的整理和K-M曲线的绘制。
以‘survival’包中的‘lung’数据集做演示：

library(survival) 
library(survminer)

#载入数据
> data("lung")
> head(lung)
  inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1    3  306      2  74   1       1       90       100     1175      NA
2    3  455      2  68   1       0       90        90     1225      15
3    3 1010      1  56   1       0       90        90       NA      15
4    5  210      2  57   1       1       90        60     1150      11
5    1  883      2  60   1       0      100        90       NA       0
6   12 1022      1  74   1       1       50        80      513       0
1
2
3
4
5
6
7
8
9
10
11
12
13

数据集中的变量和观测的具体情况可以直接使用‘?lung’来查看数据集变量的具体含义：

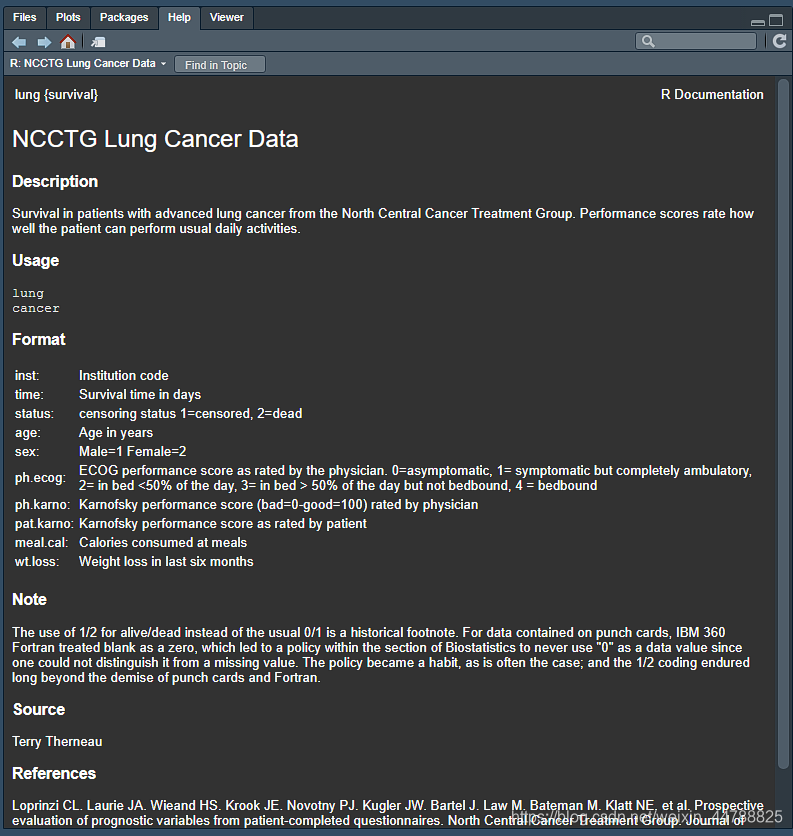
可以看出，数据集中的变量就是我们在数据收集时候的样子，接下来就三布画出K-M曲线：
第一步：将原始数据转化生存资料数据
这主要是因为我们的生存数据，从模型的角度来说，因变量是两个变量：生存时间和生存状态，所以我们要将原始数据中的时间和状态数据进行组合，以便在K-M曲线的二维坐标轴中展示三个变量的信息。

Surv(lung$time,lung$status)
?Surv
1
2

我们使用Surv()函数，其中的参数也很容易理解，一种是有了生存时间，我们就直接将这个变量放进去，再将结局变量放进去，默认两个参数就可以完成了；另一种是原始数据中只有开始和终止时间，并没有计算出生存时间，那么这个函数里就放三个参数，就成了。函数中还有很多参数，可以自定义原始数据结局的意义，可以添加左右截尾等更多的数据类型。

> Surv(lung$time,lung$status)
  [1]  306   455  1010+  210   883  1022+  310   361   218   166   170 
 [12]  654   728    71   567   144   613   707    61    88   301    81 
 [23]  624   371   394   520   574   118   390    12   473    26   533 
 [34]  107    53   122   814   965+   93   731   460   153   433   145 
 [45]  583    95   303   519   643   765   735   189    53   246   689 
 [56]   65     5   132   687   345   444   223   175    60   163    65 
 [67]  208   821+  428   230   840+  305    11   132   226   426   705 
 ……
1
2
3
4
5
6
7
8
9

后面的加号就是截尾数据的表示了。
第二步：建模
为我们的曲线建模，说是建模，在这里的实际操作可以理解为将数据的形式进行转换，变成更适合做K-M曲线的形式。

fit <- survfit(Surv(time, status) ~ sex, data = lung)
?survfit
#survfit.formula(Surv(time, status) ~ sex, data = lung)
1
2
3

这个模型看样子像单因素的模型，一个自变量，两个变量组成的因变量。又或者就是分层，这个自变量中有多少层就在K-M曲线上展示多少条曲线。
下面的注释的那个函数是上面的那个函数的扩展，作用一样，只是有更多的参数，详情可以参考帮助文档。
现在想查看这个模型到底有什么信息，一般就是summary()，用来对模型进行展示，但要想知道展示的信息是什么意思，可以使用’surv_summary()‘函数进行模型的展示，查看这个函数的帮助文档就可以知道模型里的内容都是什么了。

第三步：绘图
我们经过上面两步已经将数据准备好了，接下来直接绘图即可：

library(survminer)
ggsurvplot(fit,
           pval = TRUE, conf.int = TRUE,#可信区间带
           #cumevents=T,
           risk.table = TRUE, # 添加 risk table
           risk.table.col = "strata", # 改变这个表的颜色，一般就根据曲线的分组来
           linetype = "strata", # 改变线条的形状，一般就分组了
           surv.median.line = "hv", # 中位生存时间标识
           ggtheme = theme_bw(), # 看帮助文档，里面有很多中主题
           palette = c("#E7B800", "#2E9FDF"),
           #fun = "event" #用来做累积
)
?ggsurvplot
1
2
3
4
5
6
7
8
9
10
11
12
13

基本这个绘图函数中的参数能够满足作图的需求了，并且他还能调用ggplot2的主题设置，具体可以查看帮助文档。

二、生存过程比较

可通过生存率及其标准误对各样本的生存率进行比较，以探讨各组间的生存过程是否存在差异，对过程的检验包括：非参数检验、参数检验和半参数检验。
在比较两组符合T分布的数据时，成组T检验的主要思想是比较这两个分布的均数是否相等，当然，这是在两组等方差的基础上，所以模型检验的时候主要是检验两个模型的某个参数差异是否有统计学意义。当两组数据不符合某种分布的时候，我们用的就是非参数检验的方法，只看其数据的过程是否存在差异。
非参数检验
在生存分析中，非参数检验用的就是Log-Rank检验，其中心思想就是假定两组的生存过程相等时，所得到的理论死亡数与实际死亡数之间差异是否有有统计学意义，用的差异检验的方法就是卡方检验。
我们使用survdiff()函数进行生存过程log-rank差异检验。

surv_diff <- survdiff(Surv(time, status) ~ sex, data = lung)
?survdiff
1
2

其实在我们做生存过程描述的K-M曲线的时候，图中已经给出差异比较的P值，图中默认的就是log-rank检验。这个函数参数不是很多，使用也非常方便，包括输入输出值帮助文档都有介绍。
参数检验
生存资料的参数检验主要包括指数分布和Weibull分布，根据这两个分布拟合风险函数与各特征变量之间的回归，可以直接反映出各特征变量是否对生存风险产生影响。

三、分析危险因素

统计模型是一个经常使用的工具，可以同时分析多个因素的生存情况。另外，统计模型提供了每个因素的效应大小。
该模型的目的是同时评估几个因素对生存的影响。换句话说，它使我们能够检查特定因素在特定时间点如何影响特定事件（例如，感染，死亡）的发生率。这个因变量通常被称为危险率。预测变量（或因子）在生存分析文献中通常被称为协变量。

Cox比例风险模型的因变量由h(t)表示的危险函数表示。简而言之，危险函数可以解释为在时间t死亡的风险。可以估计如下：
h(t) = h0(t) * exp(b1X1 + b2X2 + …… + bpXp)
这是拟合的模型，之所以叫半参数模型，是因为h0(t)表示基线风险，就是在没有其他研究因素的影响下，研究对象的死亡风险，显然这个是没法计算出来的，所以就叫他半参数模型了。
模型中的回归系数bp的解释为：在其他协变量不变的情况下，协变量Xp镁每改变一个测量单位时所引起的（相对危险度或风险比）的自然对数改变量，回归系数与相对危险度的关系为：
①当协变量Xp为二分类变量0，1时，按公式，其对应的RR与回归系数的关系RR = exp(bp)，其流行病学含义为，与赋值为0的个体相比，赋值为1的个体的死亡风险增加RR-1倍
②当协变量为连续型变量时，用Xp1和Xp2表示不同情况下的取值，则RR = exp[bp(Xp1 - Xp2)]
③当协变量为多分类变量时，则可以设置哑变量，以其中一份分类为参比，估计其他分类的相对危险度。
RR > 1（即：b> 0）的协变量被称为不良预后因素
RR < 1（即：b <0）的协变量被称为良好的预后因子

建立生存分析模型：

res.cox <- coxph(Surv(time,status)~sex + age + ph.ecog + ph.karno + pat.karno + meal.cal + wt.loss,
                 data=lung)
1
2

使用coxph()函数进行Cox回归，默认的参数是最常用的，如果有需要根据实际需要，在帮助文档中查看相关参数。这个模型将所有变量纳入了，可以直接根据模型绘制森林图：

ggforest(res.cox,main="hazard ratio",
         cpositions=c(0.02,0.22,0.4),
         fontsize=0.8,refLabel="reference",noDigits=2)
1
2
3

默认Wald检验，各个参数的意义可以参考帮助文档。

不过，上述模型中没有将多分类的ph.ecog变量设置哑变量。但是在哑变量的展示上，我们可以选择森林图展示，这相较于自己再新建几个哑变量要方便些。

colon <- within(lung, {
  sex <- factor(sex, labels = c("female", "male"))
  ph.ecog <- factor(ph.ecog, labels = c("asymptomatic", "symptomatic",'in bed <50%','in bed >50%'))
})

res.cox <- coxph(Surv(time,status)~sex + age + ph.ecog + ph.karno + pat.karno + meal.cal + wt.loss,
                 data=colon)

ggforest(res.cox,main="hazard ratio",
         cpositions=c(0.02,0.22,0.4),
         fontsize=0.8,refLabel="reference",noDigits=2)
1
2
3
4
5
6
7
8
9
10
11

此时展示的就是将ph.ecog变量的四个水平设置哑变量，并且以其中一个为基线。上面那个within()函数就是用来操作数据框的。

补充：列线图

同样是构建多因素回归模型，往往我们另一个主要目的是为了对结局事件的发生风险进行预测，那么是否也可以将预测模型的结果，像森林图那样可视化地展示出来呢？
　　
　　列线图（AlignmentDiagram），又称诺莫图（Nomogram图），它是建立在多因素回归分析的基础上，将多个预测指标进行整合，然后采用带有刻度的线段，按照一定的比例绘制在同一平面上，从而用以表达预测模型中各个变量之间的相互关系。其优势在于可以直接利用图形推算出某变量的取值，如患者的指标得分或生存概率等。它在医学领域中的应用由来已久，常见的有百分位列线图和概率列线图等。百分位列线图是确定个体某指标的测量值在总体中的百分位数；概率列线图是确定某个体特定事件的发生概率，该特定事件可以是疾病的发生、复发以及预后(如死亡)等，往往由多因素二分类回归或COX比例风险模型求得。列线图是回归方程结果的可视化，常用于逻辑回归或COX回归的结果展示，依据回归的结果，按照特定的比例画出多个线段，通过做图能够便捷地推算出某个体的发病风险或生存概率。
　　　　
　　不同于森林图的绘制，我们使用森林图是用来展示我们对已有数据拟合的结果，目的是反映现有数据的分布及回归情况，仅仅作为一种描述，因此模型有意义即可。但列线图的目的是预测，在模型拟合基础上还需要模型的检验，因此在制作之前需要对预测模型的预测结果进行验证，常见的验证过程有内部验证、图形验证和外部验证。
　　内部验证可采用Bootstrap自抽样法，利用建模自身的数据来验证模型的预测效果。Bootstrap自抽样法是指对样本人群进行有放回的重复抽样，每次抽样样本数相同，这样同一个个体就有可能被抽中多次。利用Bootstrap自抽样产生的新样本去评价列线图模型的准确性，常用C-统计量来进行衡量，其值越接近于1说明列线图的预测能力越准确。
　　图形校准法的基本思想是：首先利用列线图预测出每位研究对象的生存概率，并从低到高排成一个队列，根据四分位数将队列分为4组（或者根据其他分位数分组），然后分别计算每组研究对象预测生存概率和相应的实际生存概率（由Kaplan-Meier法计算）的均值，并将两者结合起来作图得到4个校准点，最后将4个校准点连接起来得到预测校准曲线。理论上标准曲线是一条通过坐标轴原点、且斜率为1的直线，如果预测校准曲线越贴近标准曲线，则说明列线图的预测能力越好。
　　外部验证是使用另外一组研究对象的数据(即外部数据)去验证模型的预测准确性。因此在列线图的制作上，不能盲目地建立某个指标的列线图，只有当模型的预测效果得到了明确验证之后，方可对模型制作列线图，此时该列线图也会有很好的应用价值。（部分摘自临床研究方法学园地）
　　不过这些个内容在一篇里讲有些拘束了，如果有实际需要，会再分开嘻嘻讨论，现在就一个目的：绘制列线图：
第一步：载入包

library(Hmisc); library(grid); library(lattice);library(Formula); library(ggplot2) 
library(rms)
library(survival)
1
2
3

最上面的那一行，会在载入rms包的时候自动导入了。这部分独立于上面的拟合了，所以就再次加载survival包。

第二步：载入并打包数据

data("lung")

lung$sex <- 
  factor(lung$sex,
         levels = c(1,2),
         labels = c("male", "female"))## 添加变量标签以便后续说明

dd=datadist(lung)## 按照nomogram要求“打包”数据，绘制nomogram的关键步骤,??datadist查看详细说明
options(datadist="dd") 
1
2
3
4
5
6
7
8
9

第二行为变量添加标签，这个在列线图的展示的时候会有用，线段的端点显示‘male’和‘female’，而不是变量中的数值1和2。
接下来的两行打包，还没搞懂，，，，总之示例代码就是这么写的。

第三步：构建模型并绘图

## 绘制logisitc回归的风险预测值的nomogram图
f1 <- lrm(status~ age + sex, data = lung) ## 构建logisitc回归模型
?nomogram
nom <- nomogram(f1,  fun= function(x)1/(1+exp(-x)),# or fun=plogis这个函数是用来建立要预测目标
                lp=T, funlabel="Risk")

plot(nom)
1
2
3
4
5
6
7

## 绘制Cox比例风险模型预测的nomogram图
f <- cph(Surv(time, status) ~ age + sex , x=T, y=T, surv=T,time.inc=36, data=lung) # time.inc参数，与列线图中预测的几年几年生存率有关

surv <- Survival(f) # 构建生存预测函数，surv就是我们自定义的一个函数

nom <- nomogram(f, fun=list(function(x) surv(36, x),  # 36代表3*12，就是三年生存率
                            function(x) surv(60, x), 
                            function(x) surv(120, x)), 
                lp=F,
                funlabel=c("3-year survival", "5-year survival", "10-year survival"), 
                maxscale=100, # 线段上的刻度最大值，倒不是很重要，都是等比例的
                fun.at=list(c(0.95, 0.94), # 与fun对应的，是生存率线段的刻度
                            c(0.97,0.95, 0.91, 0.9, 0.88),
                            c(0.95, 0.9, 0.85, 0.8, 0.75)))

plot(nom)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

做完收工！