符号定义：

n表示样本数目；

$l\left(y_{i}, \hat{y}_{i}^{(t)}\right)$ 表示与有关的损失函数，这个损失函数是可以根据需要自己定义的；

$y_{i}$ 表示样本 i 的实际值；

$\hat{y_{i}}^{(t)}$ 表示前 t 棵决策树一起对样本 i 的预测值；

$\Omega\left(f_{t}\right)$ 表示第t棵树的模型复杂度，这里是正则化项，为了惩罚更复杂的模型（通过减小树的深度和单个叶子节点的权重值），减缓过拟合。

$\Omega(f)=\gamma T+\frac{1}{2} \lambda\|\omega\|^{2}$

T为当前子树的深度，w为叶子节点的节点值。

（2）推导

A、根据Boosting的原理简化

根据Boosting的原理：第 t 棵树对样本 i 的预测值=前 t-1 棵预测树的预测值 + 第 t 棵树的预测值

即： $\hat{y}_{i}^{(t)} = \hat{y}_{i}^{(t-1)}+f_{t}\left(\mathbf{x}_{i}\right)$

这里补充一下：Shrinkage(收缩过程)：

Shrinkage即：每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。就是说它不完全信任每一个棵残差树（达到防止过拟合的效果），它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。即给每棵数的输出结果乘上一个步长η （收缩率），如下公式所示：

$\hat{y}_{i}^{(t)}=\hat{y}_{i}^{(t-1)}+\eta f_{t}\left(\mathbf{x}_{i}\right) , 0< \eta \leq 1$

后续的公式推导都默认 η = 1。

那么最初的目标函数就可以化为： $\mathcal{L}^{(t)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(\mathbf{x}_{i}\right)\right)+\Omega\left(f_{t}\right)$

符号定义：

$f_{t}\left(\mathbf{x}_{i}\right)$ 表示第 t 棵决策树对样本 i 的预测值

B、根据二阶泰勒展开

分析：

我们知道，二阶泰勒展开公式： $f(x+\Delta x) \approx f(x) + f'(x)\Delta x + \frac{f''(x)(\Delta x)^{2}}{2}$

将上面的 $\mathcal{L}^{(t)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(\mathbf{x}_{i}\right)\right)+\Omega\left(f_{t}\right)$ 当成 $f(x+\Delta x)$ ，即把 $\hat{y}_{i}^{(t-1)}$ 当作 x ，把 $f_{t}\left(\mathbf{x}_{i}\right)$ 当作 $\Delta x$ 。

这样一来， $\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+\Omega\left(f_{t}\right)$ 就是 $f(x)$ 啦。

那么就有：

$\mathcal{L}^{(t)} =\sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

其中：

$\mathrm{g}_{\mathrm{i}}=\frac{\partial l\left(\mathrm{y}_{\mathrm{i}}, \hat{\mathrm{y}}_{\mathrm{i}}^{\mathrm{t}-1}\right)}{\partial \hat{\mathrm{y}}_{\mathrm{i}}^{\mathrm{t}-1}}$ ——表示一阶导数，是可以求出来的已知数

$\mathrm{h}_{\mathrm{i}}=\frac{\partial^{2} l\left(\mathrm{y}_{\mathrm{i}}, \hat{\mathrm{y}}_{\mathrm{i}}^{\mathrm{t}-1}\right)}{({\partial\hat{\mathrm{y}}_{\mathrm{i}}^{\mathrm{t}-1}})^{2}}$ ——表示二阶导数，是可以求出来的已知数

C、去掉常数项

因为我们的目的是要最小化目标函数，那些常数项我们可以把它们暂时搁置。

$\mathcal{L}^{(t)} =\sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

4、从目标函数到特征划分准则 + 叶子节点的值的确定

（1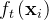） $f_{t}\left(\mathbf{x}_{i}\right)$ 的定义

XGBoost把 $f_{t}\left(\mathbf{x}_{i}\right)$ 定义为 $w_{q(x_{i})}$

其中 $q(x_{i})$ 代表了样本 i 在哪个叶子节点上，w表示叶子结点的权重（即决策树的预测值）

（2）引入真实的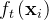 $f_{t}\left(\mathbf{x}_{i}\right)$ 和正则化项代换

$\mathcal{L}^{(t)} \approx \sum_{i=1}^{n}\left[g_{i} w_{q\left(x_{i}\right)}+\frac{1}{2} h_{i} w_{q\left(x_{i}\right)}^{2}\right]+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2}$

进一步化为： $\mathcal{L}^{(t)}=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T$

其中：

$I_{j}=\left\{i \mid q\left(x_{i}\right)=j\right\}$ 代表决策树 q 在叶子节点 j 上的取值（即表示位于第j个叶子结点有哪些样本）

这样就把累加项从样本总数变为了针对当前决策树的叶子节点。

再令 $G_{j}=\sum_{i \in I_{j}} g_{i}$ 和 $H_{j}=\sum_{i \in I_{j}} h_{i}$ ，

再次化简为：

$\mathcal{L}^{(t)}=\sum_{j=1}^{T}\left[G_{j} w_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) w_{j}^{2}\right]+\gamma T$

（3）求出 $w_{j}$ —— 定下该叶子结点的值

因为我们的目的是最小化目标函数，因此我们对上式求导，令其为0。

$w_{j}^{*}=-\frac{G_{j}}{H_{j}+\lambda}$

即我们应该将叶子结点的值 $w_{j}$ 设为 $-\frac{G_{j}}{H_{j}+\lambda}$

（4）目标函数的最优解——与信息增益的连接

${\mathcal{L}^{(t)}}^{*}=-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T$

这个 ${\mathcal{L}^{(t)}}^{*}$ 又叫结构分数，类似于信息增益，可以对树的结构进行打分。

信息增益：更能确定多少——目标函数：预测对了多少

（5）特征划分准则——“信息增益”

$\operatorname{Gain}=\frac{1}{2}\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_{L}+G_{R}\right)^{2}}{H_{L}+H_{R}+\lambda}\right]-\gamma$

其中 L 下标是值划分到左子树时的目标函数最优值，R 下标是值划分到右子树时的目标函数最优值。在实际划分时，XGBoost会基于“Gain最大”的节点进行划分。

第一部分是新的左子叶的分数（即该节点进行特征分裂后左子叶的目标函数）；第二部分是新的右子叶的分数（即该节点进行特征分裂后右子叶的目标函数）；第三部分是原来叶子的分数（即该节点未进行特征分裂前的目标函数）；第四部分是新增叶子的正则系数。

体现的意义即为：判断分裂节点后的信息增益（第一部分+第二部分）是否大于未分裂的情况，并且考虑到模型会不会太复杂的问题（如果增加的分数小于正则项，节点不再分裂）。

5、从目标函数到加权分位法（实现对每个特征具体的划分）

（1）引入原因

比如说，有一个特征A是一个离散的连续变量，有100个不同的值，范围是[1,100]。那么如果选择特征D来分裂节点时，需要尝试100种不同的划分，一个一个算然后再对比Gain，可以是可以，但会导致算法的效率很低。

XGBoost为了实现可以不用尝试每一种的划分，只选取几个值进行尝试，提出了加权分位法。

（2）“特征值重要性”的提出

为了得到值得进行尝试的划分点，我们需要建立一个函数对该特征的特征值进行"重要性"排序。根据排序的结果，再选出值得进行尝试的特征值。

（3）目标函数到平方损失

我们前面得到的目标函数长这样：

$\mathcal{L}^{(t)} =\sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

我们把 $\frac{1}{2}h_{i}$ 提出来，变成：

$\mathcal{L}^{(t)} =\sum_{i=1}^{n}\frac{1}{2} h_{i}\left[2\frac{g_{i}}{h_{i}} f_{t}\left(x_{i}\right)+ f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

然后因为 $g_{i}$ 和 $h_{i}$ 都是已知数，相当于常量，我们给他加上它们的相关运算，在后面再给他减掉一个常数，结果不变。

$\mathcal{L}^{(t)} =\sum_{i=1}^{n}\frac{1}{2} h_{i}\left[f_{t}(x_{i}) - \frac{g_{i}}{h_{i}}\right]^{2}+\Omega\left(f_{t}\right) + C$

C为常数项

现在我们得到的式子即为：真实值为 $\frac{g_{i}}{h_{i}}$ ，权重为 $h_{i}$ 的平方损失项+正则化项+常数项

（4）特征值重要性排序函数

因此，我们可以得出结论：一个样本对于目标函数值的贡献，在于其 $h_{i}$ 。因此可以根据 $h_{i}$ 对特征值的“重要性”进行排序。XGBoost提出了一个新的函数，这个函数用于表示一个特征值的"重要性"排名：（这里的特征值表示：某个等待判断分裂的节点属性，中的某个取值）

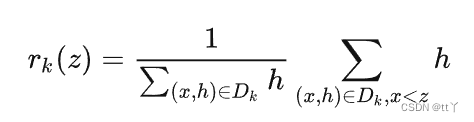
其中：

$D_{k}$ ：第k个特征的每个样本的特征值（ $x_{nk}$ ）与其相应的 $h_{i}$ 组成的集合；

$(x_{ik},h_{i})$ ：表示第 i 个样本对于第k个特征的特征值，和其对应的 $h_{i}$ ；

$D_{k} = \left \{(x_{1k},h1), ... ,(x_{nk},h_{n}) \right \}$
$r_{k}(z)$ 的分母：第k个特征的所有样本的 $h_{i}$ 的总和；
$r_{k}(z)$ 的分子：所有特征值小于z的样本的 $h_{i}$ 总和；

式子表示的意义是：特征值小于z的样本特征重要性分布占比

（5）切分点寻找

之后对一个特征的所有特征值进行排序。在排序之后，设置一个值 ϵ （采样频率）。这个值用于对要划分的点进行规范。对于特征k的特征值的划分点 $\left \{s_{k1},s_{k2},...,s_{kl} \right \}$ 有，两个相连划分点的 $r_{k}$ 值之差的绝对值要小于 ϵ （为了让相邻的划分点的贡献度都差不多）。同时，为了增大算法的效率，也可以选择每个切分点包含的特征值数量尽可能多。

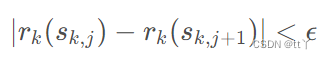
（6）计算分裂点的策略

基于加权分位法，我们有两种策略进行分裂点的计算：全局策略和局部策略。

A、全局策略

即在一棵树的生成之前，就已经计算好每个特征的分裂点。在整个树的生成过程当中，用的都是一开始计算的分裂点。这也就代表了使用全局策略的开销更低，但如果分裂点不够多的话，准确率是不够高的。

B、局部策略

根据每一个节点所包含的样本，重新计算其所有特征的分裂点（即边建立树边重新更新分裂点）。

因为在一棵树的分裂的时候，样本会逐渐被划分到不同的结点中（即每个结点所包含的样本，以及这些样本有的特征值是不一样的）。因此，我们可以对每个结点重新计算分裂点，以保证准确性，但这样会使局部策略的开销更大，但分裂点数目不用太多，也能够达到一定的准确率。

（1）在分裂点数目相同，即 ϵ 相同的时候，全局策略的效果比局部策略的效果差；

（2）全局策略可以通过增加分裂点数目，达到逼近局部策略的效果

三、XGBoost对缺失值的处理

对于特征A，我们首先将样本中特征A的特征值为缺失值的样本全部剔除。然后我们正常进行样本划分。

最后，我们做两个假设：一个是缺失值全部归在左子节点；一个是归在右子节点。哪一个得到的增益大，就代表这个特征最好的划分。

Note：对于加权分位法中对于特征值的排序，缺失值不参与（即缺失值不会作为分裂点，gblinear将缺失值视为0）

四、XGBoost的优缺点

1、优点

（1）精度高

XGBoost对损失函数进行了二阶泰勒展开，一方面为了增加精度，另一方面也为了能够自定义损失函数，二阶泰勒展开可以近似许多损失函数。（对比只用到一阶泰勒的GBDT）

（2）灵活性强

XGBoost不仅支持CART，还支持线性分类器；

XGBoost还支持自定义损失函数，只要损失函数有一二阶导数。

（3）防止过拟合

A、正则化

XGBoost在目标函数中加入了正则项，用于惩罚过大的模型复杂度，有助于降低模型方差，防止过拟合。
B、Shrinkage（缩减）

主要是为了削弱每棵树的影响，让后面有更大的学习空间，学习过程更加的平缓。

C、列抽样

在建立决策树的时候，不用再遍历所有的特征了，可以进行抽样。

一方面简化了计算，另一方面也有助于降低过拟合。

（4）缺失值处理

（5）并行化操作

有一些不相关可以很好的支持并行计算

2、缺点

时间复杂度和空间复杂度都较高（预排序过程）。

欢迎大家在评论区批评指正，谢谢~

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/319623

XGBoost详解（原理篇）

一、XGBoost简介

二、XGBoost原理

1、基本组成元素

2、整体思路

（1）训练过程——构建XGBoost模型

（2）测试过程

3、目标函数

（1）最初的目标函数