繁依Fanyi0

这个屌丝很懒，什么也没留下！

热门标签

R统计绘图-线性混合效应模型详解(理论、模型构建、检验、选择、方差分解及结果可视化)

作者：繁依Fanyi0 | 2024-03-27 09:40:01

踩

一、基础理论

二、数据准备

三、构建线性混合效应模型(LMMs)

3.1 lme4线性混合效应模型formula

一、基础理论

各个数据模型都包含一些假设，当数据满足这些假设时，使用这些模型得到的结果才会更准确。比如广义线性模型要满足“线性”和“独立性”等条件。为了适应更多数据类型，开发出了各种模型，可根据数据情况，选择合适的模型。比如，如果数据不满足“线性”，则可考虑广义可加模型；如果不满足“独立性”，则可以考虑混合效应模型(mixed effect model)。

多水平模型同时包含多个分类因子数据，最主要特点就是非独立性，在多个水平上都存在残差，因此适合混合效应模型，总的来说，其思想就是把高水平上的差异估计出来，这就使得残差变小，估计的结果更为可靠。混合效应模型又称随机效应模型(Random Effect model)，分层线性模型，随机系数模型，方差成分模型等。

比如，一份包含不同施肥处理的多土层微生物数据，其中不同施肥处理与不同土壤深度即是嵌套数据(多水平数据)。

如果用线性模型分析不同施肥处理间微生物群落的差异，则没有考虑到不同土壤深度的微生物群落的差异，暗含了假设：不同土壤深度的微生物群落随不同施肥处理变化的截距与斜率都是相同的。不同土壤深度土壤的微生物群落差异就被线性模型归类到误差中去了。

如何解决这一问题呢？其中一种方法就是使用固定效应模型(Fixed Effect Model)，即将不同土壤深度的微生物群落结构随不同施肥处理变化的截距差异和斜率差异都估计出来。在土壤深度分类较少时可以这么做，将次级分类水平作为虚拟变量回归，3分类，则估计2个截距差异和斜率差异。当次级分类水平过多时，需要估计的参数太多，用虚拟变量就会消耗太多的自由度，估计结果不可靠，此时即可考虑使用混合效应模型。

固定效应与随机效应因子之间没有明显的分类，但显然随机效应因子要是分类数据，且数据跟随机效应存在相关性。有文章推荐随机效应的分类水平最好大于5类，因为当分类水平较少时，模型对方差的估计不太准确。当随机因子大于1个时，随机因子间的关系也需要注意，根据随机因子间关系，可能包括交叉(Crossed)、部分交叉或嵌套(nested)。

混合效应模型也分为线性混合效应模型、广义线性混合效应模型和非线性混合效应模型。此文章介绍使用R中lme4包进行线性混合效应模型分析。

线性混合效应模型假设：

1. 残差应该是正态分布的-可以适当放宽，前提是预测值与残差没有相关性，

2. 残差的方差是同质的-非常重要的假设；

3. 随机效应的观测是相互独立的；

4. 自变量与因变量存在线性关系；

5. 自变量间不存在相关性-方差膨胀因子筛选或者数据降维。

当然，对数据中异常点的检测也是很有必要的。

二、数据准备

此套数据是嵌套数据，包含分类因子depth和tillage。嵌套数据中包含多个分类自变量，数据是非独立性的，模型构建时考虑使用混合效应模型。选择pH为因变量。


# 设置工作路径
#knitr::opts_knit$set(root.dir="D:\\EcoEvoPhylo\\MEM\\LMM")# 使用Rmarkdown进行程序运行
Sys.setlocale('LC_ALL','C') # Rmarkdown全局设置
#options(stringsAsFactors=F)# R中环境变量设置，防止字符型变量转换为因子
library(tidyverse)
library(rstatix)
library(car)
library(lme4)
library(lmerTest) # 模型固定效应系数检验
library(multilevelTools) # 模型诊断检验
library(extraoperators)
library(JWileymisc) # 模型诊断及APAStyler以表格形式输出模型结果
library(effectsize) # 计算标准化回归系数
library(influence.ME) # 检测高影响观测点
library(GGally)
# 2.1 导入数据
env <- read.csv("env.csv",row.names = 1)
env %>% head
# 2.2 计算均值与标准误
env %>%
  group_by(condition) %>%
  get_summary_stats(names(env[4:ncol(env)]),type="mean_se") %>%
  left_join(env[1:3],by = "condition") -> data
data %>% sample_n_by(tillage,size=2)

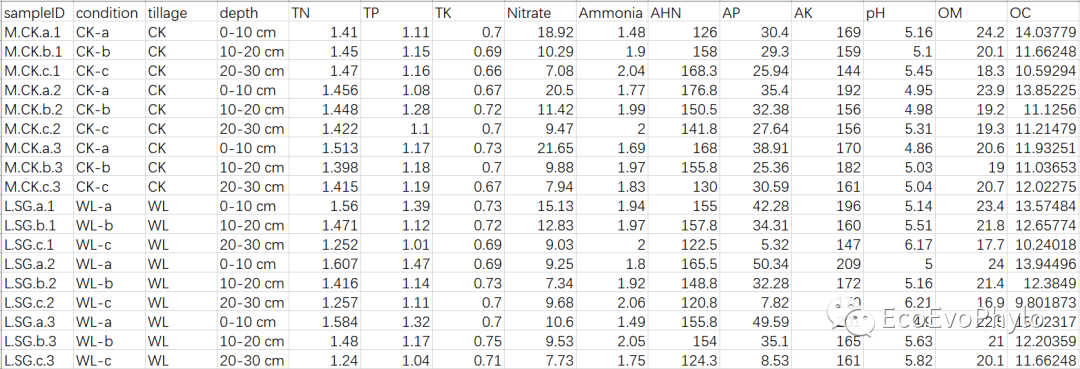
图1|原始数据表，env.csv。

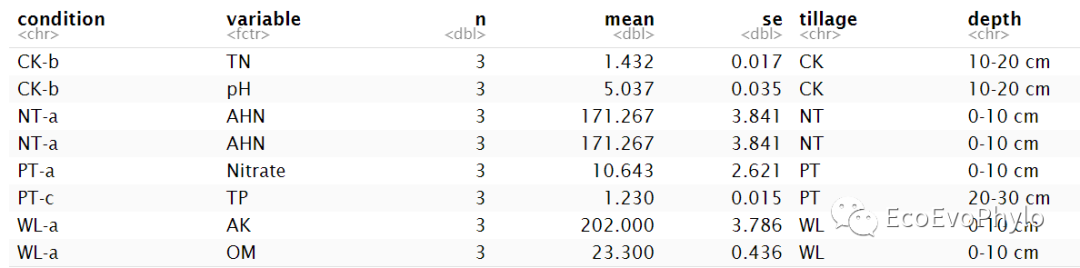
图2|均值-标准误差计算结果，data。


# 2.3 数据探索-查看数据是否适合进行线性混合效应模型分析
## 2.3.1 ICC-组内相关系数计算
icc1 <- iccMixed("pH","depth",env)
icc1
icc2 <- iccMixed("pH","tillage",env)
icc2

图3|组内相关系数计算结果，icc1。intra-class correlation coefficient (ICC)将变量差异分解为组内和组间差异，此处将depth作为随机截距，Sigma列依次为随机截距方差(组间差异)，残差(组内差异)。ICC=0表示差异全部来自组内个体差异，ICC=1表示变量差异全部来自组间，此处ICC=0.5062462表明depth水平间的方差挺大的，可以考虑使用混合效应模型。


## 2.3.2 计算有效样本大小
nEffective(n = length(unique(env$depth)),
           k = nrow(env)/length(unique(env$depth)),
           dv = "pH",
           id = "depth",data=env
                  )

图4|effective sample size。对数据提供的有效独立样本数量的估计。N为独立的样本数量，k为每个独立样本的重复测量次数。


## 2.3.3 因变量分布、极端值探索
### 将因变量按照分类因子进行均值分解
#### depth
tmp1 <- meanDecompose(pH ~ depth, data = env)
tmp1
tmp1$`pH by depth`
tmp1$`pH by residual`
plot(testDistribution(tmp1[["pH by depth"]]$X,
                      extremevalues = "theoretical", ev.perc = .001),
     varlab = "Between Depth")
plot(testDistribution(tmp1[["pH by residual"]]$X,
                      extremevalues = "theoretical", ev.perc = .001),
     varlab = "Within Depth")#图中黑色点表示极端值。
#### tillage
tmp2 <- meanDecompose(pH ~ tillage, data = env)
tmp2
do.call(cowplot::plot_grid, c(lapply(names(tmp2), function(x) {
  plot(JWileymisc::testDistribution(tmp2[[x]]$X), plot = FALSE, varlab = x)$Density
}), ncol = 1))

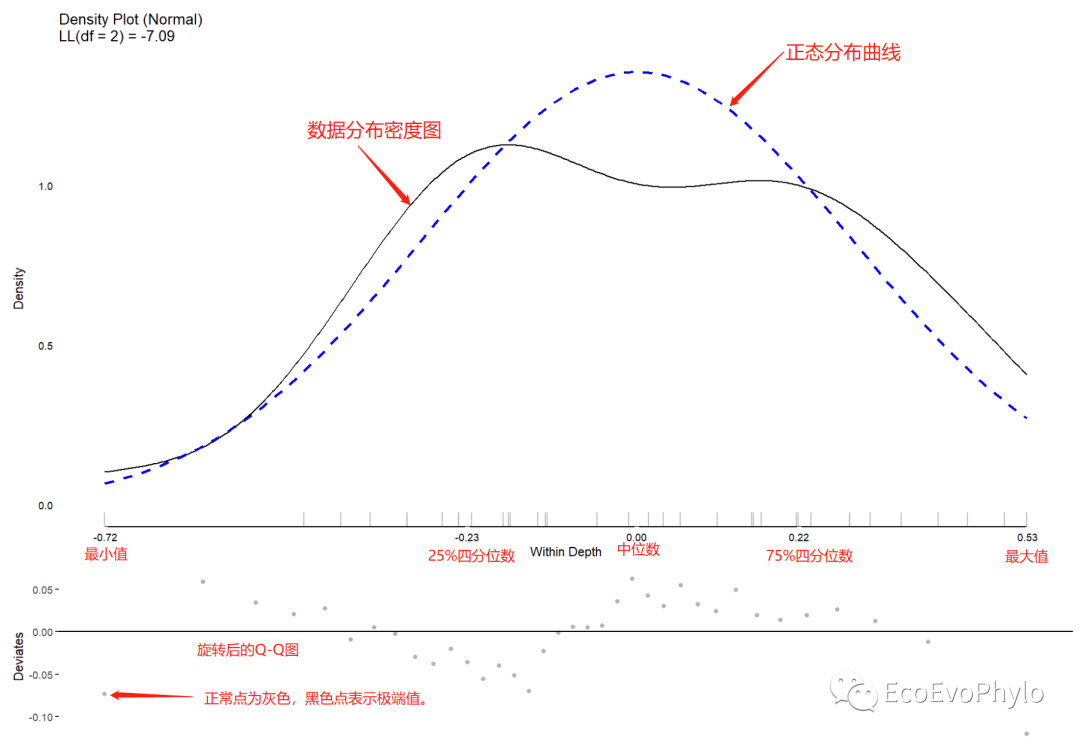
图5|均值分解图，Within Depth。


## 2.3.4 散点图可视化数据分布趋势
### width format转为long format
(env %>%
  gather(key = "variable",value = "value",-condition,-tillage,-depth) %>%
  rstatix::reorder_levels(variable,
                 order =c("pH","OM", "OC", 
                          "Ammonia", "Nitrate","AHN",  
                          "TN", "TP", "TK", 
                          "AP", "AK"
                           )) -> data.p)
### 设置颜色
col1 <- colorRampPalette(colors =c("#56B1F7","#132B43"),space="Lab") 
### 绘制分面-分组散点图
(data.p %>%  ggplot2::ggplot(aes(
  x = factor(tillage,levels=c("CK","WL","NT","PT")),
  y = value,
  color= factor(depth,levels = unique(data.p$depth))))+
  geom_point(
    position = position_dodge(0.8), #调整site之间的宽度距离。
    width = 0.5,size = 1
  )+
  scale_color_manual(name = "Depth",
                     # values = ggsci::pal_d3("category10")(10),
                     values = col1(3),
                     breaks = c(unique( as.character(data.p$depth) )))+
  facet_wrap(.~variable,ncol = 4,scales = "free")+
  labs(x = NULL, y = NULL) -> p1) # 绘图函数加上括号，赋值给变量的同时，会在屏幕上显示。
### 输出pdf图到本地
ggsave("p1.pdf", p1, device = "pdf",width = unit(10,"cm"),height = unit(8,"cm"))

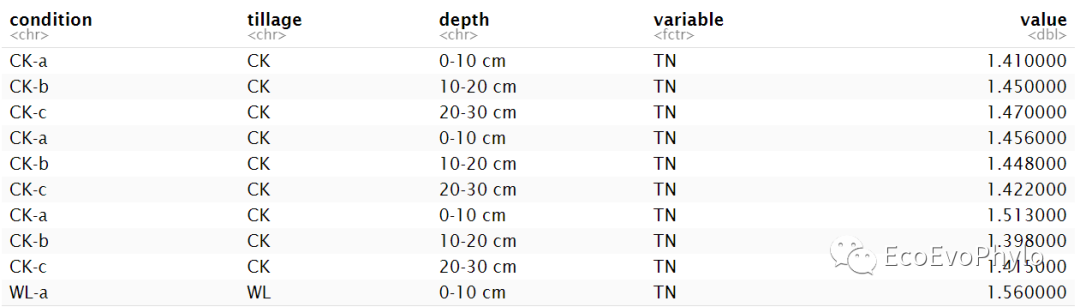
图6|long format格式数据表，data.p。

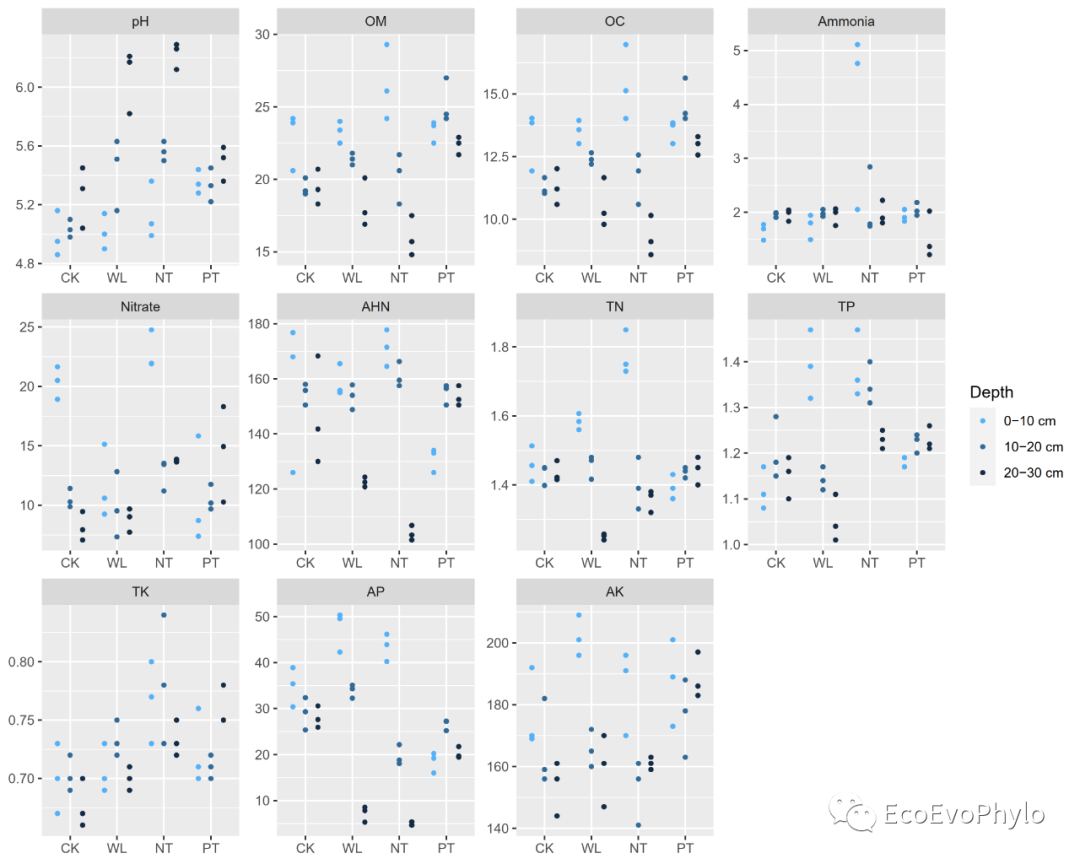
图7|可视化pH数据分布，p1.pdf。


## 2.3.5 绘制变量相关性图
### 设置绘图颜色
cols <- ggsci::pal_jco()(7) 
### 绘制相关性图
my_density <- function(data, mapping) {
 ggplot(data = data, mapping = mapping) +
 geom_density() 
} # 自定义函数
(
 ggpairs(env,columns = 4:14, 
 ggplot2::aes(color = tillage), # 按分组信息分别着色、计算相关性系数和拟合
 upper = list(continuous = "cor"), 
 lower = list(continuous = wrap("smooth",method = "lm",se = FALSE)), # se = FALSE,不展示置信区间 
 diag = list(continuous = my_density))+
 ggplot2::scale_color_manual(values = cols)+
 theme_bw() -> p2
 )
### 输出pdf图到本地
pdf("p2.pdf",height = 20,width = 20,family = "Times")
print(p2)
dev.off()

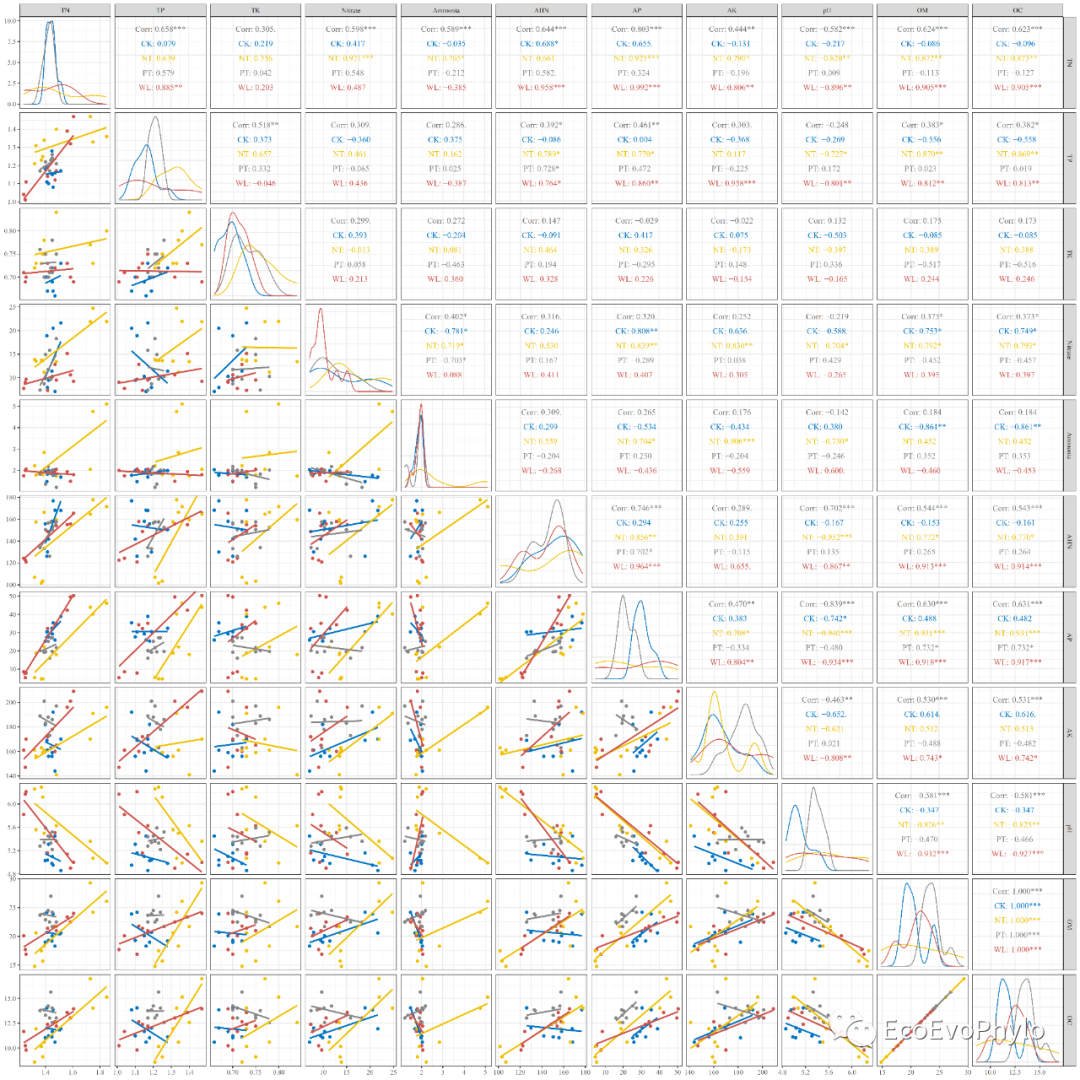
图8|变量相关性线性拟合图，p2.pdf。由图可知，很多两两变量的关系在tillage水平中的截距和斜率是不一致的。

三、构建线性混合效应模型(LMMs)

混合效应模型是指包含固定效应和随机效应的模型，固定效应部分就是线性模型模式，随机效应可以分为随机截距模型和随机斜率模型两大类。固定效应因子与随机效应因子没有很严格的区分，更多是根据自己的研究目的进行设置，最后模型都要满足线性混合模型的假设以及符合科学性。

此处使用lme4执行线性混合效应模型，(1+depth)表示depth是随机因子，截距随机。lme4包提供了进行线性混合效应模型、广义线性混合效应模型和非线性混合效应模型拟合和分析的功能。nlme包也可用于混合效应模型的建模。随机效应项在函数表达式中表现为(expr|factor)，expr是一个线性或广义线性等模型公式，factor是随机因子。lme4中用不同的formula区分交叉或嵌套数据。

此过程是模型矩阵与分组因子的一种特殊交互，用以确保固定因子模型矩阵对于分组因子各水平都有不同的影响。分组因子效应被建模为未观察到的随机变量，而不是未知的固定参数。随机截距模型的截距的平均值和标准差是要估计的参数，模型将随机效应的任何非零均值合并为固定效应参数。函数默认执行限制性极大似然估计(REML)，REML假设固定效应结构是正确的,在比较具有不同固定效应的模型时，应该使用最大似然(ML)。因为ML不依赖于固定效应的系数。但ML对两个具有嵌套随机结构的模型进行比较时，对方差项的估计量存在偏差。因此，具有相同固定效应的模型，使用REML比较随机效应不同的模型。

模型(固定效应系数和模型比较)显著性检验方法可选(效果从弱到强)：

1）Wald Z-tests，固定效应系数显著性检验，适合大数据集；

2）Wald t-tests (but LMMs need to be balanced and nested)；

3）Likelihood ratio tests，只能用于ML拟合模型，可比较固定效应或随机效应不同的两个模型，那个能更好的拟合数据；

4) Kenward-Roger and Satterthwaite approximations for degrees of freedom，可比较两个固定效应模型的差异显著性;

5）MCMC，不适合随机斜率模型;

6）parametric bootstrap confidence intervals。

当样本量足够时p值获取可以通过LRT或Wald t检验模型，但样本量较少时更推荐使用Kenward-Roger(只能用于REML)，Satterthwaite approximations(REML或ML)或parametric bootstrap。

3.1 lme4线性混合效应模型formula

随机截距模型：模型中只包含随机截距；随机斜率模型：模型中包含随机斜率。


# 3.1.1 线性回归模型
fm0 <- lm(pH ~ tillage + AP, 
           data = env)
fm0 %>% summary
# 3.1.2 随机截距模型-depth的各水平都有对应的截距，模型会估计这些截距的均值和标准差。
control <- lmerControl(
  optCtrl = list(
   algorithm = "NLOPT_LN_NELDERMEAD",
   xtol_abs = 1e-12,
   ftol_abs = 1e-12,
   check.conv.singular = .makeCC(action = "ignore", 
                                 tol = 1e-12)
  )
)
fm1 <- lmer(pH ~ tillage + AP + (1|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm1 %>% summary
# 3.1.3 随机截距模型-添加先验prior截距均值
fm2 <- lmer(pH ~ tillage + AP + offset(AP) + (1|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm2 %>% summary
# 3.1.4 混合效应模型：相关随机系数和截距模型
##lme4假设同一随机效应项的所有系数项是相关的。
fm3 <- lmer(pH ~ tillage + AP + (1+tillage|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm3 %>% summary
# 3.1.5 指定不相关随机系数和截距模型-相当于(tillage||depth)
fm4 <- lmer(pH ~ tillage + AP + (1|depth)+(0+tillage|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm4 %>% summary
# 3.1.6 考虑交互效应的随机截距模型-相当于(1|tillage) +(1|tillage:depth)。
##depth必须嵌套于tillage,不同tillage水平，depth间的pH不独立且具有差异。
fm5 <- lmer(pH ~ AP + (1|tillage/depth),
           data = env,
           REML = FALSE,
           control = control)
fm5 %>% summary
# 3.1.7 两组分类因子混合效应模型-如果同一样本在两个随机因子处都有观测， 则是交叉数据。
##将tillage与depth合并因子condition纳入分析，则是交叉数据。
##此处观察的是所有实验处理(tillage)和采样区域(condition)的对因变量的影响。
fm6 <- lmer(pH ~ AP + (1|tillage) + (1|condition), 
           data = env,
           REML = FALSE,
           control = control) # 可以与fm6进行比较，观察两者差异。
fm6 %>% summary
# 3.1.8 混合效应模型-depth各水平在tillage和AP都有不同斜率和不同截距。
fm7 <- lmer(pH ~ AP + tillage + (tillage + AP|depth), 
           data = env,
           REML = FALSE,
           control = control)
fm7 %>% summary
# 3.1.9 随机斜率模型
fm8 <- lmer(pH ~ tillage + AP +(0 + tillage|depth), # 0表示固定截距。
           data = env,
           REML = FALSE,
           control = control)
fm8 %>% summary

出现boundary (singular) fit: see help('isSingular')警告，要么修改随机效应，要么改用贝叶斯混合效应模型。

模型构建都不是一蹴而就的,当自变量较多时，可以先构建全模型，模型检验不显著且不是研究关注核心的自变量，可以删除后，重构模型

3.2 随机截距模型构建及检验


# 3.2.1 构建随机截距模型
control <- lmerControl(
  optCtrl = list(
   algorithm = "NLOPT_LN_NELDERMEAD",
   xtol_abs = 1e-12,
   ftol_abs = 1e-12,
   check.conv.singular = .makeCC(action = "ignore", 
                                 tol = 1e-12)
  )
)
##lmerTest::lmer()输出结果包含模型系数检验的p值，lme4::lmer()输出结果则不包含。
fm1 <- lmerTest::lmer(pH ~ tillage + A + (1|depth), 
           data = env,
           REML = FALSE,
           control = control) 
# 3.2.2 模型诊断
## JWileymisc::modelDiagnostics()
fmd1 <- modelDiagnostics(
  fm1,
  ev.perc = 0.001 # 可设置为0-1，表示理论分布的比例，超出该比例的值被视为极值。
  )
### 绘制残差诊断图
plot(fmd1,ask=FALSE,nrow=3)
### 提取极端值-如果有极端值，则可使用update()函数删除该数据点且更新模型。
fmd1$extremeValues # 此数据没有异常值，所以为null。

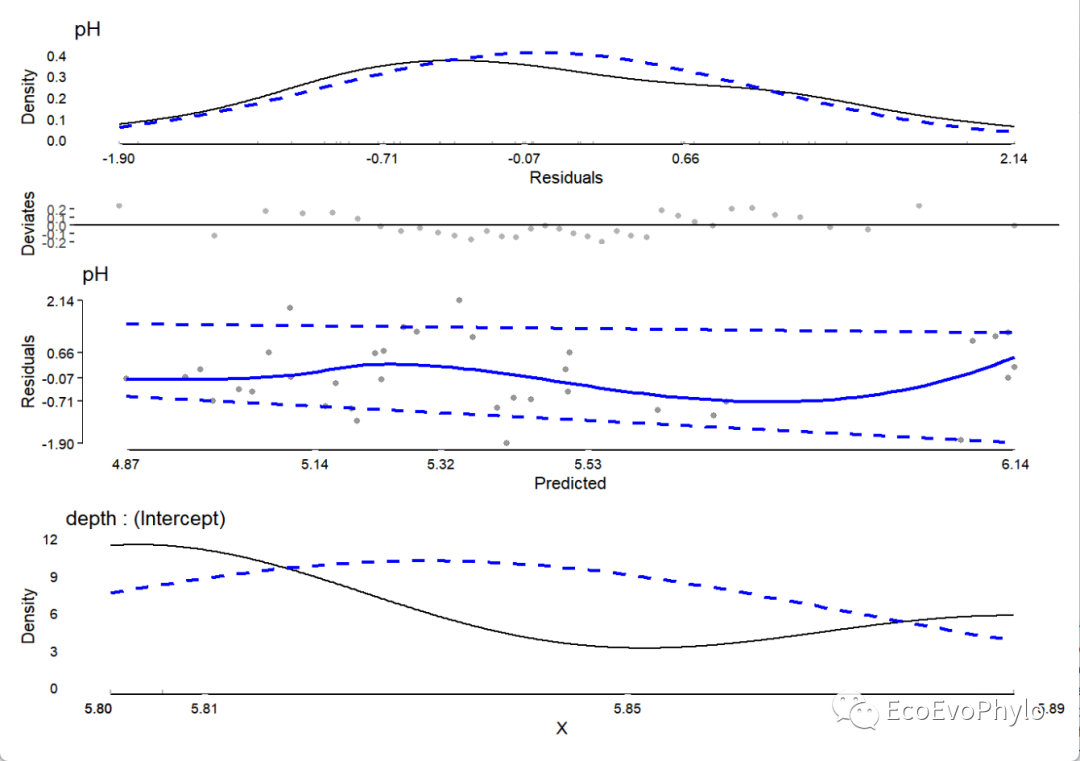
图9|随机截距模型检验图。拟合模型之后，还要检验模型是否符合线性混合效应模型的假设。模型检验图的数量根据固定效应和随机效应数量变化。此模型的模型检验组合图中的第一幅图是残差的分布，应该要大致符合正态分布。第二幅图是残差-预测值图可以大致看出数据是否符合“同方差性”，残差值应该围绕0均匀分布，没有明显的分布趋势。最后，蓝色虚线表示预测值残差的第10%和第90%分位数（根据分位数回归模型估计），如果残差的方差是同质的，蓝色虚线应该是平坦且彼此平行的。如图所示，图中残差分布有明显的趋势，不太适合线性模型，可以改换非线性混合模型，或者残差异质性不严重，也可忽略。最后一幅图是depth随机截距的单变量分布。模型敏感性分析是一种评估模型结果对于参数变化或假设的变化的稳定性和影响的方法，模型假设检验就是敏感性分析的重要内容。


## sjPlot包可以对模型假设检验结果进行可视化
fmd1.sj <- sjPlot::plot_model(fm1, type = "diag")
# fmd1.sj[[1]] # 残差正态分布及离群值检验。
# fmd1.sj[[2]]$depth # 随机效应的Q-Q图。
# fmd1.sj[[3]] #残差正态分布检验。
# fmd1.sj[[4]]#残差方差同质性检验。
### 拼图并输出到本地
(fm1.assumptions <- cowplot::plot_grid(fmd1.sj[[1]],fmd1.sj[[2]]$depth, fmd1.sj[[3]], fmd1.sj[[4]],
                   labels = c("A", "B","C","D")))
cowplot::save_plot(
  "fm1.assumptions.png",
  fm1.assumptions)
## performance::check_model()也可对模型假设检验结果进行可视化
theme_set(theme_classic(base_size = 6)) # windows太小，绘图会报错，先将ggplot2绘图的字体设置小一点。
pdf("check_model.pdf",width = unit(12,"cm"),height = unit(12,"cm"),family = "Times")
performance::check_model(fm1) 
dev.off()

图10|随机截距模型假设检验图，fm1.assumptions.png。sjPlot::plot_model()可以对很多模型的假设检验和模型参数进行绘图，更多参数细节可以?plot_model查看函数帮助信息。R中进行相同统计分析的函数很多，使用函数可视化时，还是要知道函数使用的什么数据以及对数据进行过怎样的处理。

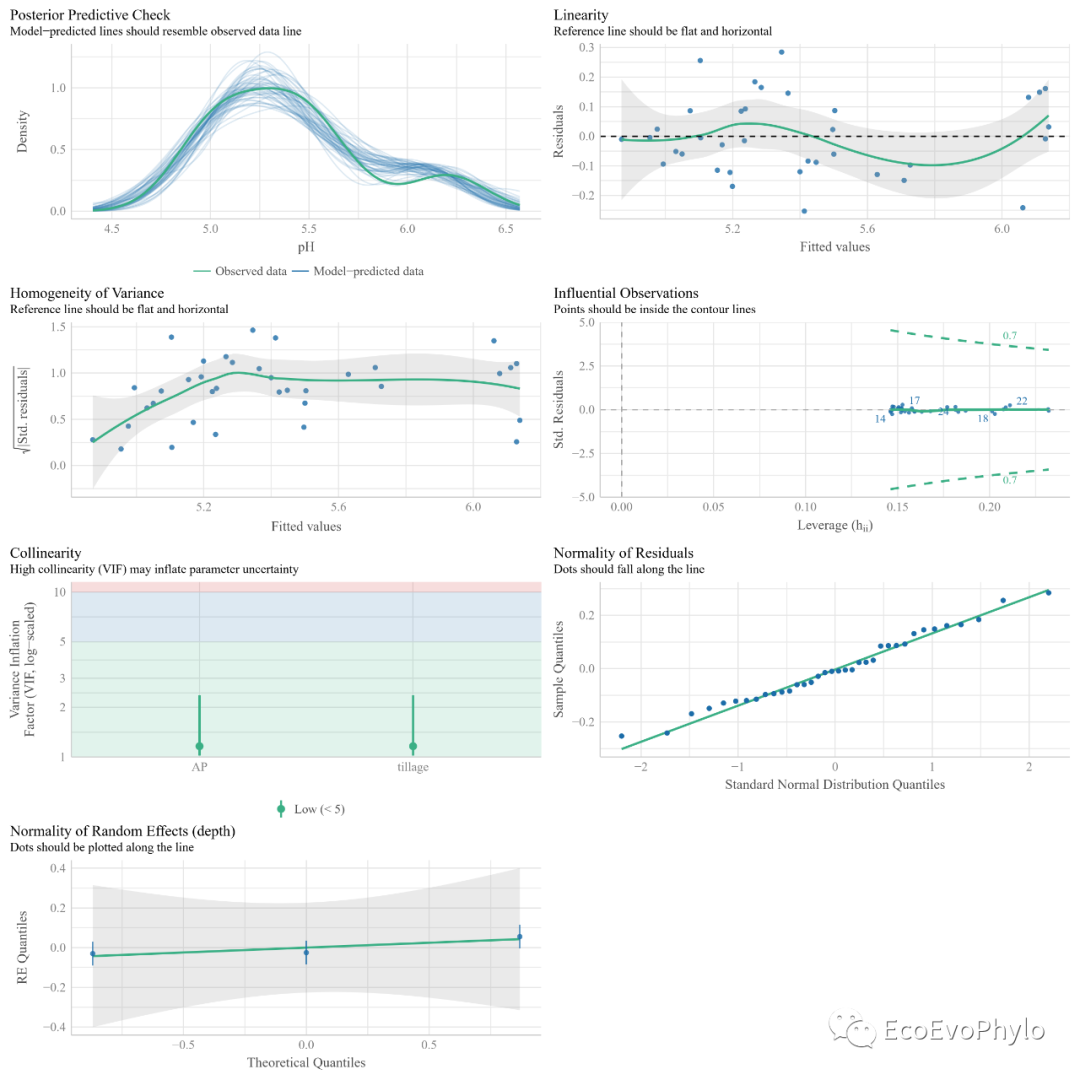
图11|随机截距模型假设检验图，check_model.pdf。performance::check_model()的模型检验结果更全，图也更美观。


## 检验模型自变量是否具有共线性-一般阈值为5或10等
car::vif(fm1) # 此模型的两个自变量共线性不强。

图12|方差膨胀因子计算结果。vif输出结果包括variance-inflation(VIF,模型所有项df =1),generalized variance-inflation factors (GVIF, df>1)和自由度校正GVIF值。


## 计算unadjusted ICC和adjusted ICC
performance::icc(fm1) # 有时也称为variance partition coefficient (VPC)。

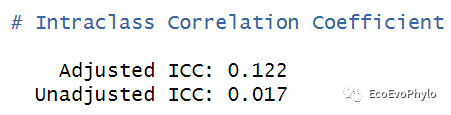
图13|组内相关系数计算结果。模型未校正ICC代表模型中只包含随机效应时的组内相关系数，adjusted ICC表示模型同时考虑随机效应和固定效应时，随机因子不同水平之间的相关性。ICC的取值范围在0到1之间，其值越小代表随机因子水平内的相似性并不比水平间的相似性高，表示没有必要将此因子设置为随机因子。


## 模型高影响力观测点检测：influence.ME::dfbetas.estex()
##leave-one-out  diagnostics，重点观察改变模型系数超过其原值一半的观测点。
### 逐个删除观测点，计算数据改变后模型固定系数的变化。
alt.est <- influence(fm1,obs=TRUE)
alt.est$or.fixed # 原模型固定因子系数
alt.est$alt.fixed # 去除某一观测点后，模型固定因子的系数
alt.est$or.se
alt.est$alt.se
### 计算数据改变后模型与全模型的固定系数的标准化差异：
##计算公式为：(原始模型参数-删除观测点后模型参数)/删除观测点后模型的标准误差。
##dfbeta的绝对值越大，删除该观测后的模型系数改变越大。cut-off值一般选2/sqrt(n),n表示检测的观测点的数量。此处为2/sqrt(36)。
##to.sort = 1表示按照截距变化值降序排列。
dfbetas.estex(alt.est,sort=TRUE,to.sort = 1 ) 
### 基于完整数据集的（混合效应）回归模型与删除了某些观测点的模型之间参数估计的百分比变化。以绝对值显示。
##R包文章中的计算公式为：(原模型参数-删除某一个观测后模型参数)/原模型参数*100%。
##pchange()实际计算公式为：(删除某一个观测后模型参数-原模型参数)/删除某一个观测后模型参数*100%。因此此函数计算有误，不需要参考。了解计算原理，可自行提取数据进行计算。
pchange(alt.est, parameters = 0, abs=TRUE) # 删除第8个样本后，tillagePT的参数估计变化较大。
### cook's距离计算-表示模型固定效应参数受观测点的影响程度。
##一般阈值设置为4/n,此处为4/36。
cooks.distance(alt.est)
### 删除某观测点前后固定效应系数显著性检验结果的变化
#alt.est2 <- influence(fm1,group="depth") # 也可以直接检测随机效应的各分类水平删除后，固定效应系数是否发生变化。
influence.ME::sigtest(alt.est, test=1.96)$Intercept
sigtest(alt.est, test=1.96)$tillageNT
sigtest(alt.est, test=-1.96)$tillagePT
sigtest(alt.est, test=1.96)$tillageWL
sigtest(alt.est, test=1.96)$AP #四个固定效应系数的显著性都未发生变化。

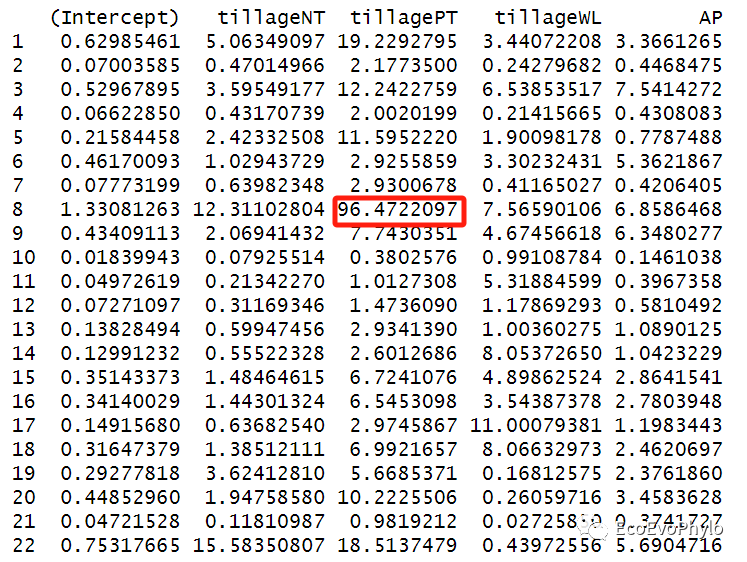
图14|随机截距模型检验图。第8个观测点删除后，tillagePT系数变化过大，可使用sigtest进行检验删除该观测点之后，固定效应参数的显著性是否发生变化，看是否需要删除该观测点。

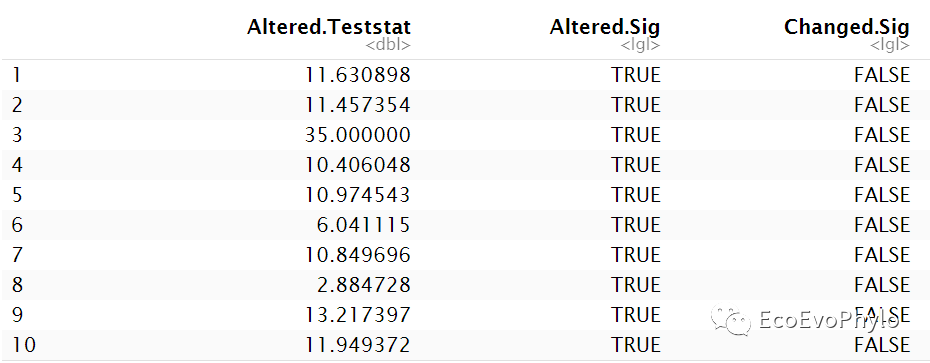
图15|删除某观测点后模型截距参数显著性的变化。列内容依次代表删除某一观测之后，模型截距参数值(Altered.Teststat)、参数检验显著性(Altered.Sig)以及删除前后截距参数检验结果是否发生变化(Changed.Sig)。Altered.Sig的结果会随着函数中test值的正负而发生改变，Changed.Sig不会。输出结果中只需要看Changed.Sig列即可。因此使用R包，一定要知道他的计算原理，不能完全相信输出结果。


### 绘制观测点模型影响力图
plot(alt.est, which="dfbetas")
plot(alt.est, which="cook", 
     sort=TRUE,cutoff = 4/36,
     xlab="Cook´s Distance",
     ylab="Samples")
plot(alt.est, which="pchange")
plot(alt.est, which="sigtest")
### 删除第8观测点，更新模型及重新诊断模型-此处没有需要删除的观测点，此步只是展示如何更新模型。
fm1.2 <-  update(fm1, data = env[-8,])
fmd1.2 <- modelDiagnostics(fm1.2, ev.perc = .001)
plot(fmd1.2, ask = FALSE, nrow = 3)
fmd1.2$extremeValues

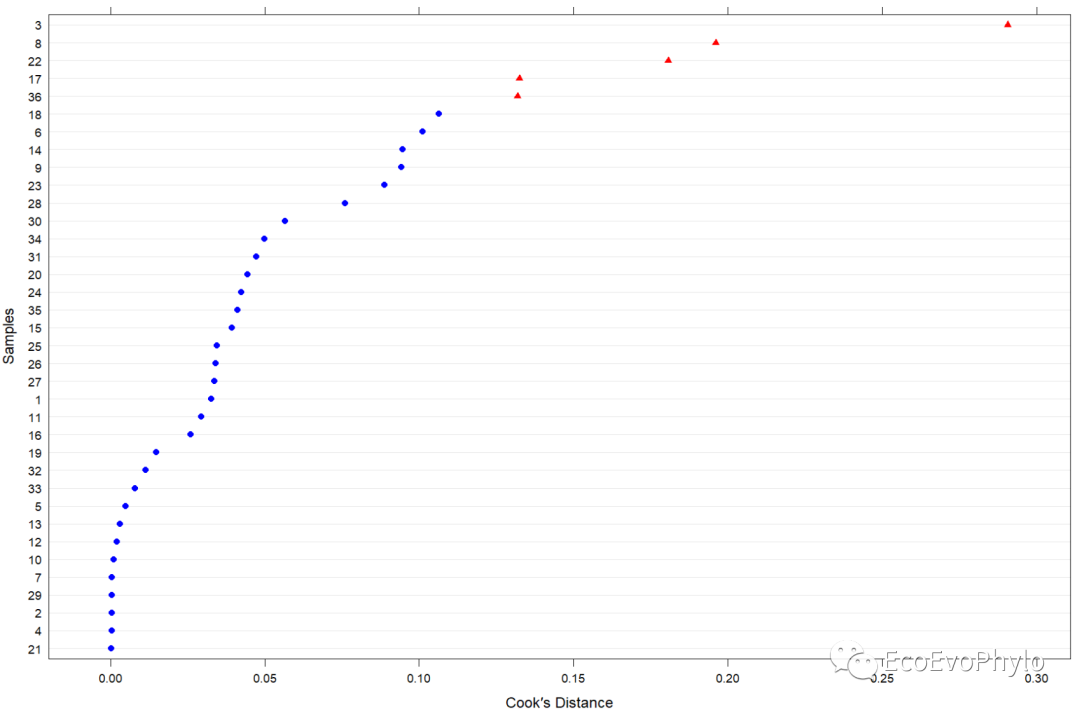
图16|cook's距离图。某一观测点对模型参数的影响力，红色三角形表示超过设置阈值的观测点。influence.ME包中函数的计算公式和更多输出结果意义，请查看https://journal.r-project.org/archive/2012-2/RJournal_2012-2_Nieuwenhuis~et~al.pdf。个人更推荐使用car包检测模型的高影响力点。


## 推荐使用car包检测模型的高影响力点
car::influencePlot(fm1)

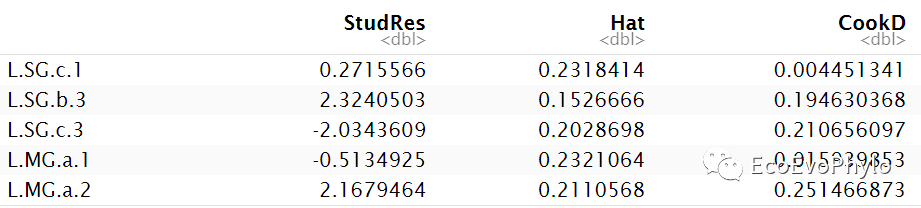
图17|car::influencePlot()输出的高影响观测值。推荐使用car包检测模型假设。更多线性模型假设检验信息，可参考R统计绘图-多重线性回归(最优子集法特征筛选，leaps)。

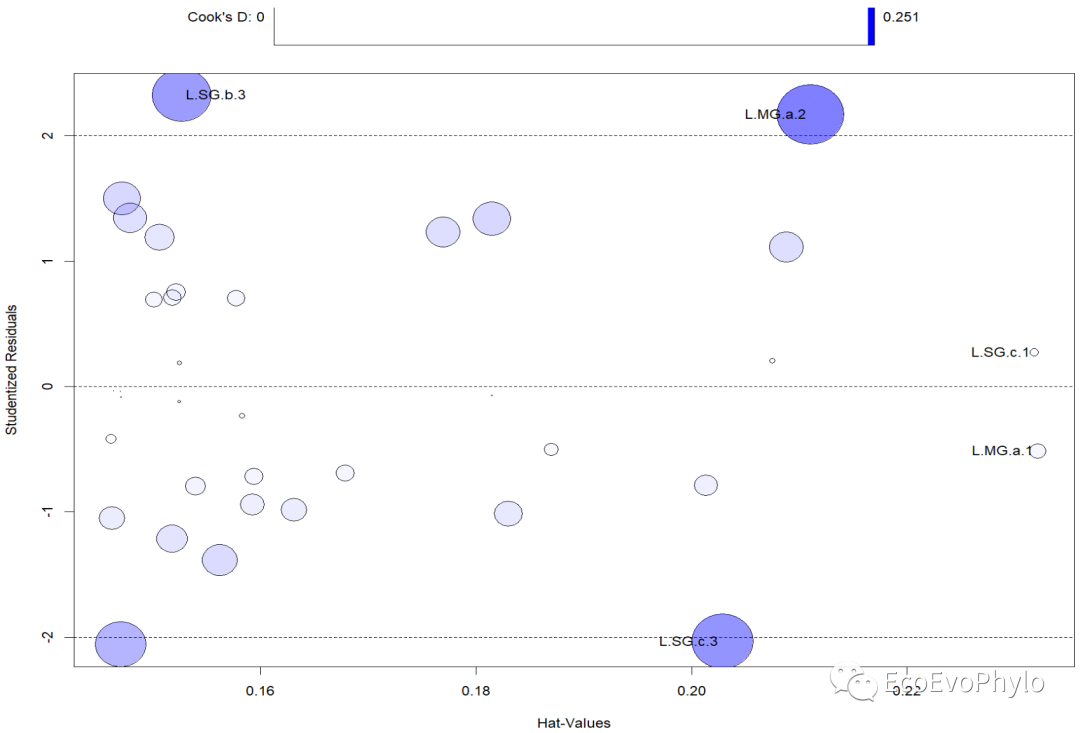
图18|car::influencePlot()输出的离群点、高杠杆值和强影响点的信息整合图。图中纵坐标超过+2或小于-2的观测点可被认为是离群点，横坐标超过0.2或0.3的观测点有高杠杆值(通常为预测值的组合)。圆圈大小与影响成比例，圆圈很大的点可能是对模型参数的估计造成的不成比例影响的强影响点。没有通过检验的点将会在图后列出。


# 3.2.3 模型检验
##lmer()没有直接提供整体模型检验结果，可使用其它函数计算。
##multilevelTools包的modelTest()、lmerTest包的ranova()和JWileymisc包modelPerformance()能提供更多用于出版的检验信息，如果固定效应的边际R方等
## summary()-模型系数t检验-Satterthwaite's degrees of freedom method
fm1.res <- fm1 %>% summary
fm1.res
#vcov(fm1) %>% cov2cor() # 固定系数的相关矩阵。
## 计算固定效应方差及随机效应解释方差的比例：总方差=固定效应方差+随机效应方差+残差。
(fix.var <- var(model.matrix(fm1)%*%fixef(fm1))) # 固定效应方差：参考
0.002452/(fix.var+0.002452+0.017687)*100 # 1.686511%

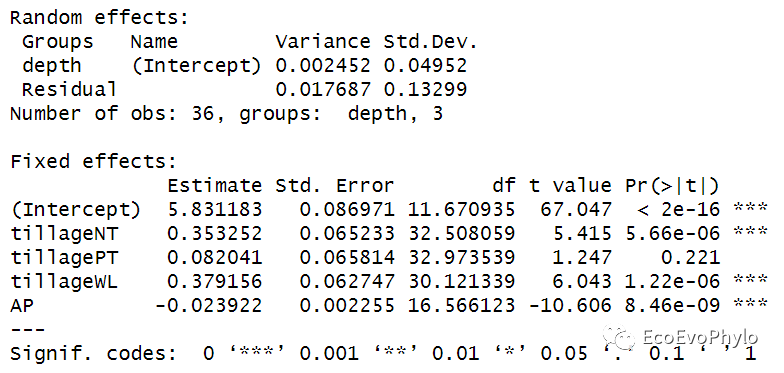
图19|fm1.res结果解释。summary结果中包含AIC、BIC、LRT等模型评估值，可用于对使用相同算法(ML或REML)的模型间的比较。输出结果中还包括随机效应方差和残差，固定效应系数(截距+斜率)统计量及t检验结果以及固定效应相关性矩阵。模型的截距是5.831183,是depth三个水平截距的均值。Fixed effects中4个斜率的绝对值都大于对应误差，表明固定效应能与0区分开，系数可用。Fixed effects中tillageNT的斜率0.353252表示模型估计从CK到NT，pH的含量预测增加0.353252。tillagePT的系数0.082041的意义也是一样，从CK到PT，pH预计增加0.082041。模型中tillageCK是作为哑变量，模型系数为0，如果没有设置因子水平，函数则会根据字母顺序选择某个分类变量水平作为哑变量。AP的系数-0.023922表示AP每增加一个单位，pH降低0.023922。总方差=固定效应方差+随机效应方差+残差。depth的随机效应方差表示depth对土壤pH的影响，模型已给出0.002452，残差也已给出0.017687，固定效应的方差需要自己计算一下，可按照张霜老师的推文进行计算(https://blog.sciencenet.cn/home.php?mod=space&uid=3442043&do=blog&id=1326172),值为 0.1252499。最后计算出depth能解释pH的1.686511%的方差[0.002452/(0.002452+0.017687+ 0.1252499)*100]。Correlation of Fixed Effects中输出了模型固定系数的相关矩阵，固定系数的Std.Error是估计方差的平方根。vcov(fm1)可以查看固定系数的估计方差,vcov(fm1) %>% cov2cor()即是固定系数的相关矩阵。具体意义可查看：https://library.virginia.edu/data/articles/correlation-of-fixed-effects-in-lme4。

summary()没有对随机效应的方差和整体模型进行检测，接下来介绍随机效应和模型检验的结果。anova()函数可以通过LRT检验进行不同模型的比较。pbkrtest包提供函数可进行只针对REML模型的Kenward-Roger法检验。car::Anova()也可对线性混合效应模型进行检测，且方差分析方法和参数设置更多。


## 模型固定效应F检验
### Type III anova table with p-values for F-tests based on Satterthwaite's.
anova(fm1)#与anova(fm1,type = "marginal")结果相同。
### 基于Kenward-Roger法的模型检验只针对REML
fm1.1 <- lmer(pH ~ AP + tillage + (1|depth),
            data = env,
            REML = TRUE,
            control = control)
if(requireNamespace("pbkrtest", quietly = TRUE))
anova(fm1.1, type=2, ddf="Kenward-Roger")
### Anova中的方差分析方法和参数设置更多-Analysis of Deviance Table (Type II Wald chisquare tests)
car::Anova(fm1)

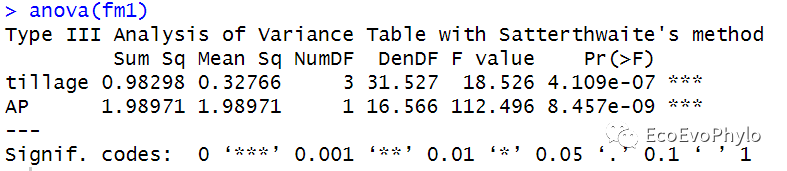
图20|模型的Satterthwaite's检验结果。anova函数中只有一个模型时，则会输出模型固定因子的F检验结果，结果显示三个固定因子的方差检验结果都存在统计学意义。

图21|模型的Kenward-Roger法检验结果。Kenward-Roger法只能用于REML模型，当样本量较小时，更推荐使用此方法。

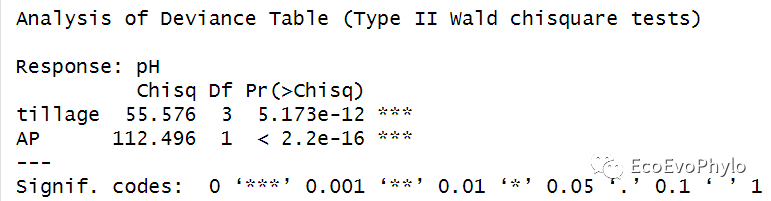
图22|模型的Wald chisquare法检验结果。默认检验方法与anova()不同。更多检验方法可以查看：http://link.springer.com/article/10.3758%2Fs13428-016-0809-y。


## ranova()-模型随机效应LRT检验
ranova(fm1)

图23|模型随机效应检验结果。ranova()对模型随机效应的似然比检验(LRT)结果支持(1 | depth)的方差不显著不为0，则表示depth间无差异，这与depth对模型较低的方差解释率是对应的，则可以把考虑去除模型中的depth的随机截距。如果方差显著不为零，此随机效应则应该保留。

JWileymisc、modelsummary、export和sjPlot等包可以对模型进行检验、提取模型结果以及以文字、表格或图形展示出版需要统计信息：统计值、置信区间、p值等。


## modelTest()可以对模型进行检验并以表格形式提取出版需要统计信息：统计值、置信区间、p值等
fm1.da <- JWileymisc::modelTest(fm1)
fm1.da$FixedEffects # 固定效应检验
fm1.da$RandomEffects # 随机效应检验
fm1.da$EffectSizes # 固定效应统计值，包括marginal R2、conditional R2、cohen’s F2和卡方检验结果。
fm1.da$OverallModel$Performance # 整体模型检验，包括AIC、BIC、MarginalR2和ConditionalR2等值。
# names(modelTest(fm1)) # 输出结果中包含的列表名。
# APAStyler(modelTest(fm1)) # 可用于去除极端值前后的模型结果比较:APAStyler(list(Original = mt, `Outliers Removed` = mt3))。
APAStyler(modelTest(fm1),
          format = list(
            FixedEffects = "%s, %s (%s; %s)",
            RandomEffects = c("%s", "%s (%s, %s)"),
            EffectSizes = "%s, %s; %s"),
          digits = 3,
          pcontrol = list(digits = 3, stars = FALSE,
                          includeP = TRUE, includeSign = TRUE,
                          dropLeadingZero = TRUE))

图24|模型综合检验结果，modelTest。数据结果包括AIC/BIC等模型评估指标，随机效应方差和模型残差，固定效应统计量等。输出结果缩写代表的含义，可通过??modelTest查看函数的帮助文件。AIC (Akaike Information Criterion)；BIC (Bayesian Information Criterion)；LL (Log Likelihood)；LLDF (degrees of freedom for log likelihood)；Sigma (residual standard deviation)；R2 (R2 variance accounted for in the sample)；F2 (Cohen’s f2 effect size, calculated as [R2/(1−R2)])；AdjR2 (Sample size adjusted R2, a better estimate of population variance accounted for)；F (model F test)；FNumDF (numerator degrees of freedom for model F test)；FDenDF (denominator degrees of freedom for model F test)；P (p value for model F test)。


## tab_model()以html形式输出模型参数检验结果。
(sjPlot::tab_model(fm1,
                  collapse.ci = TRUE,
                  p.style = "numeric_stars",
                  file="fm1.html")) # 以html表格形式输出模型参数，，使用的是Nakagawa's R2。

图25|模型参数检验结果，fm1.html。数据结果包括AIC/BIC等模型评估指标，随机效应方差和模型残差，固定效应统计量和Marginal R2/Conditional R2等。不同函数的主要差异在于R2的计算方法，其他参数只是小数点位数设置差异。sjPlot::tab_model()使用performance::r2()为混合效应模型计算Nakagawa's R2。


## modelsummary()-能直接将模型参数表格输出为word文档,可以方便的进行多个模型的参数提取及比较，还可以并行提取。
(modelsummary::modelsummary(list("fm1" = fm1),
                            stars=TRUE,
                            estimate = "{estimate} ({std.error}){stars}", # 展示模型固定效应统计量、标准误和显著性标记。
                            statistic = "conf.int",# 展示置信区间。
                            output = "fm1.docx")) # 使用的performance::r2()计算的R2,会与其他函数的提取的Marginal R2 / Conditional R2值不一样。

图26|模型参数检验结果，fm1.docx。数据结果包括AIC/BIC等模型评估指标，随机效应方差和模型残差，固定效应统计量和边际效应等。modelsummary()使用performance::r2()为混合效应模型计算Nakagawa's R2,会与其他函数的提取的Marginal R2 / Conditional R2值有些微差别。其他参数只是小数点位数设置差异。

3.3 随机截距模型分析结果解释及可视化


# 3.3.1 模型系数解释
coef(fm1) # 未标准化模型系数。
effectsize(fm1) # 标准化回归系数，不是很有必要，实际预测时使用的是未标准化回归系数。
fixef(fm1) # 提取未标准化固定效应系数。
ranef(fm1) # 提取随机效应系数。

图27|未标准化模型系数，coef(fm1)。提取系数可以看到，随机截距模型中，随机效应depth有三个不同的截距系数，各水平对应的其它自变量的斜率系数都是一样的。系数具体含义已在fm1.res中提过，这里不再赘述。

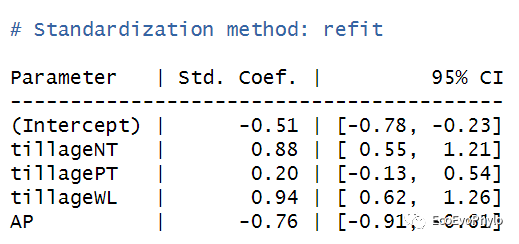
图28|标准化固定因子模型系数，effectsize(fm1)。对自变量和因变量同时经过标准化处理后消除了量纲、数量级等差异的影响，然后构建模型得到的就是标准化回归系数，因此，标准化回归系数可以直观比较不同自变量对因变量的作用大小，但不一定具有统计学意义。未标准化回归系数的意义则是，在其它自变量保持不变的情况下，该自变量变化一个单位导致的因变量的变化量。当自变量中存在分类变量时，使用标准化回归系数那一解释系数意义，且在实际预测时，模型使用的是未标准化系数，因此标准化回归系数可用可不用。


# 3.3.2  Estimated marginal means (Least-squares means)-在其它因素保持不变的情况下的固定因子水平的均值。
emmeans::emmeans(fm1, ~tillage) # tillage各水平的pH最小二乘均值。
emmeans::emmeans(fm1, ~AP)
emmeans::emmeans(fm1, ~AP|tillage) # 两者交互
# env %>% group_by(`tillage`) %>% select(pH) %>% rstatix::get_summary_stats() %>% data.frame()

图29|估计边际均值结果，emmeans(fm1, ~tillage)。估计边际均值结果中的emmean列表示固定因子变量各水平以及固定定量变量的pH的最小二乘均值，tillage的结果中WL的emmean值最大，表示pH在NT和WL的值更大，pH均值在两者中也是更大的，只有些微差别。结果解释可参考：https://www.zhihu.com/question/370213292。


# 3.3.3  Post-hoc / Contrast Analysis
library(knitr)
## tillage水平间估计边际均值的两两比较
emmeans::emmeans(fm1, pairwise ~ tillage, adjust = "bonferroni")$contrasts %>% 
  tidy() %>% 
  mutate_if(is.numeric, ~round(., 4)) %>% 
  kable()
## tillage与AP交互效应的估计边际均值的两两比较
emmeans::emmeans(fm1, pairwise ~ tillage * AP, adjust = "bonferroni")$contrasts %>% 
  tidy() %>% 
  mutate_if(is.numeric, ~round(., 4)) 
## 估计边际均值事后检验结果绘图
emmeans::pwpp(emmeans::emmeans(fm1, pairwise ~ tillage * AP, adjust = "bonferroni"), type = "response")+theme_minimal()

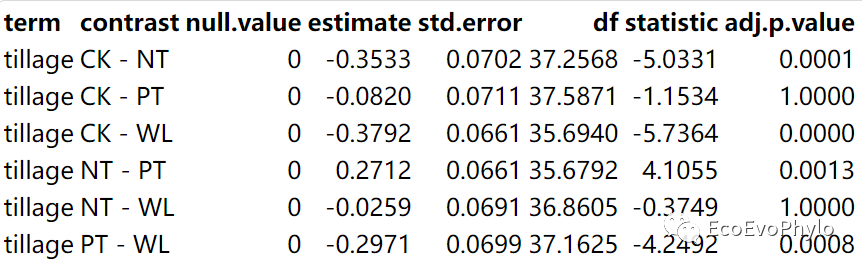
图30|tillage水平间估计边际均值的两两比较。

图31|tillage水平间估计边际均值的两两比较。

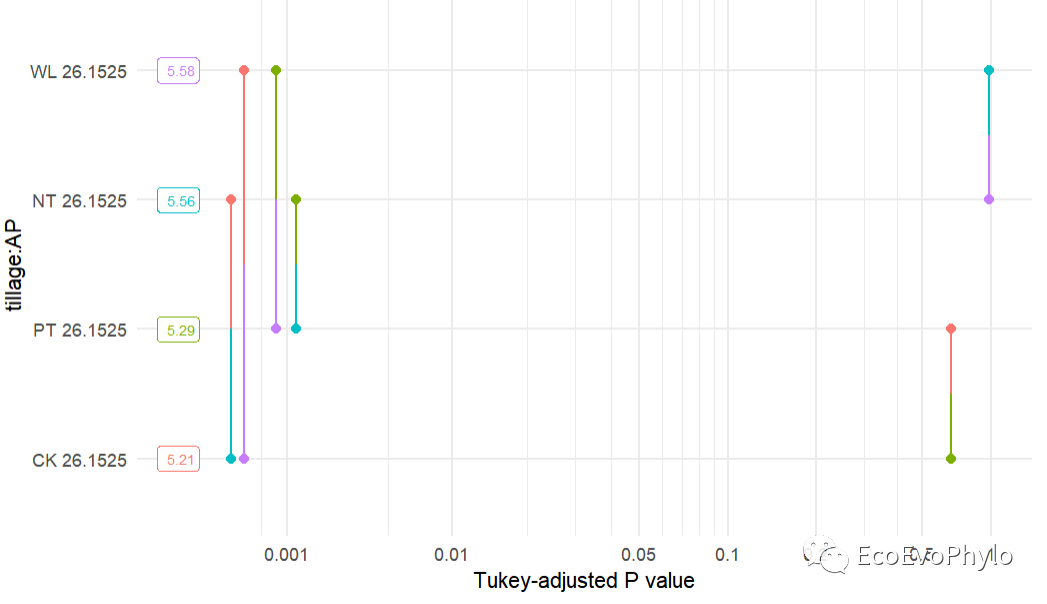
图32|估计边际均值事后检验结果绘图。


# 3.3.4 方差分解-不同方法计算出的R2结果会有差异，但是趋势都是一致的。
## 方法一：R2计算模型整体的MarginalR2和ConditionalR2 
R2(fm1)
## 方法二：modelTest()会计算模型整体和固定效应的MarginalR2和ConditionalR2。
fm1.da <- JWileymisc::modelTest(fm1)
### 模型整体的MarginalR2和ConditionalR2，与R2()计算结果一致。
fm1.da$OverallModel$Performance %>%
  select(Model,MarginalR2,ConditionalR2)
### 固定效应的MarginalR2和ConditionalR2。
fm1.da$EffectSizes %>%
  select(Variable,MarginalR2,ConditionalR2)
## 方法三：r2()会计算模型整体的Nakagawa's MarginalR2和ConditionalR2。
performance::r2(fm1,version=TRUE)
## 方法四：MuMln包的r.squaredGLMM()只提供模型整体的marginal R2和conditional R2。
# install.packages("D://software//MuMIn_1.47.8.zip",'repos = NULL')
MuMIn::r.squaredGLMM(fm1) #计算模型的边际及条件R方,程辑包‘MuMIn’需要>= 4.2.0。
## 方差分解：glmm.hp包的glmm.hp():"hierarchical partitioning"
glmm.hp::glmm.hp(fm1)$hierarchical.partitioning
## 方差分解结果绘图
### 方差分解绘图数据提取
r2 <- round(glmm.hp::glmm.hp(fm1)$r.squaredGLMM,4)
fix.r2 <- glmm.hp::glmm.hp(fm1)$hierarchical.partitioning
(plot_data <- data.frame(
  variable = c("tillage","AP","depth","Unexplained"),
  explain = c(
    fix.r2[,3],
    r2[2]-r2[1],
    1-r2[2])*100, #用百分数显示。
  p.value = c(
    anova(fm1,type = "marginal")[,6],
    ranova(fm1)[2,6],
    1),
  response = "pH"
))
### 方差分解结果绘图
(plot_data %>% 
  ggplot2::ggplot(
    aes(y=response,x=explain,fill=reorder(variable,-explain)))+
  geom_bar(position = "stack",
           stat = "identity",
           width=0.4)+
  geom_text(aes(label = ifelse(p.value >0.05,"","*")),size=2.5)+
  ggthemes::theme_base()+
  labs(y="",x="Variation (%)")+
  scale_fill_brewer(type = "qual",palette = "Set2",
                    breaks= c("AP","tillage","depth","Unexplained"), #自定义图例顺序
                    guide = guide_legend(title = "", byrow = TRUE,nrow=1 )
                              )+
  scale_x_continuous(expand = c(0,0),
                     limits = c(0,100),
                     breaks = seq(0,100,25),
                     labels = seq(0,100,25))+
  theme(axis.ticks.y = element_blank(),
        plot.background = element_blank(),
        panel.grid = element_blank(),
        legend.position = "top",
        plot.margin=unit(c(2,1,0.25,1),'cm'),
        legend.background = element_rect(color=NULL)) -> var.decom)
ggsave("var.decom.pdf",var.decom,device = "pdf",family="Times",width = 7,height = 3)

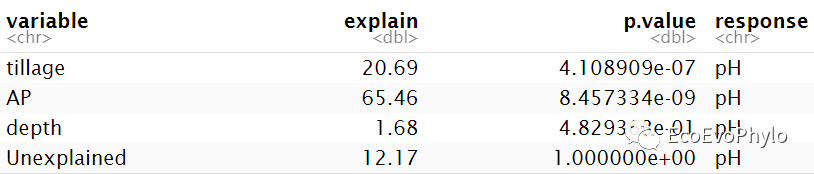
图33|方差分解结果表。此处选择的glmm.hp包的glmm.hp()方差分解的结果。hierarchical partitioning法的方差分解结果，Unique表示固定因子的解释的方差，与fm1.da$EffectSizes中计算的固定效应的边际R2值相近。Average.share表示层次分割计算的共享方差，Individual表示固定因子的单独MarginalR2，I.perc(%)是固定因子独自解释因变量的方差占模型MarginalR2的比例。r.squaredGLMM的方差与R2的计算结果有些微差异，但是趋势是一致的。方差分解有很多算法，选用方法的时候应该弄清楚背后的原理，理论文章是要引用的。

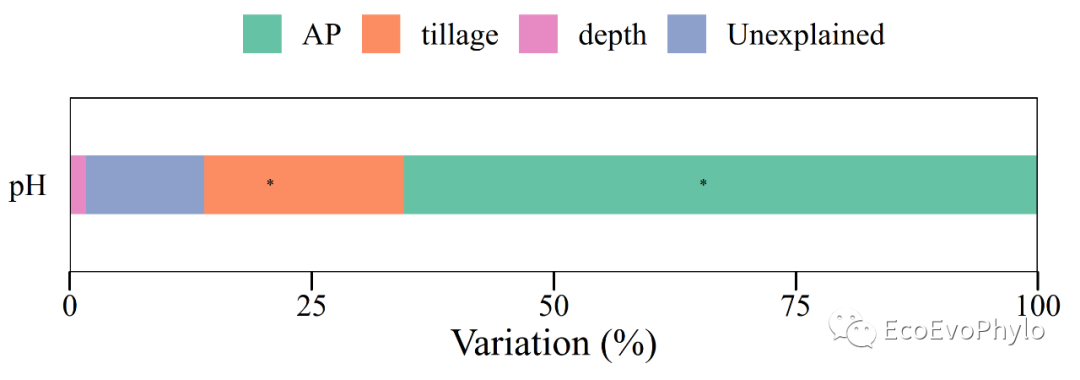
图34|方差分解结果绘图。柱子中的星号表示固定效应参数检验显著。


# 3.3.5 绘制效应图(effect plot)
## 绘制随机效应水平间变化：绘制随机截距和斜率与模型总体截距和斜率的差异。
lattice::dotplot(ranef(fm1, condVar=T))
## 绘制固定效应预测效应图。
plot(effects::allEffects(fm1)) 
## 绘制模型预测效果图。
performance::check_predictions(fm1)

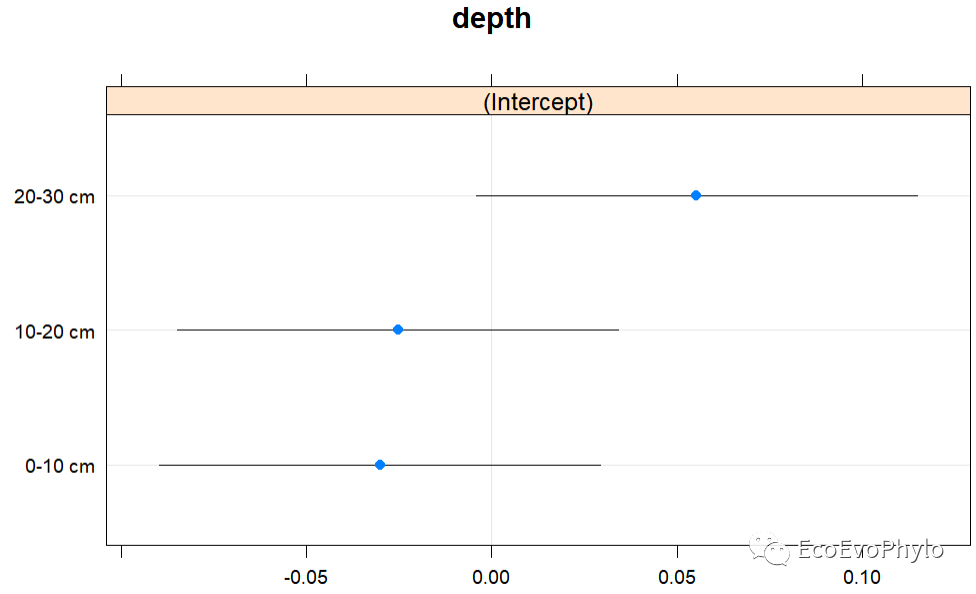
图35|随机效应系数散点图。随机截距模型只有截距的随机效应参数。

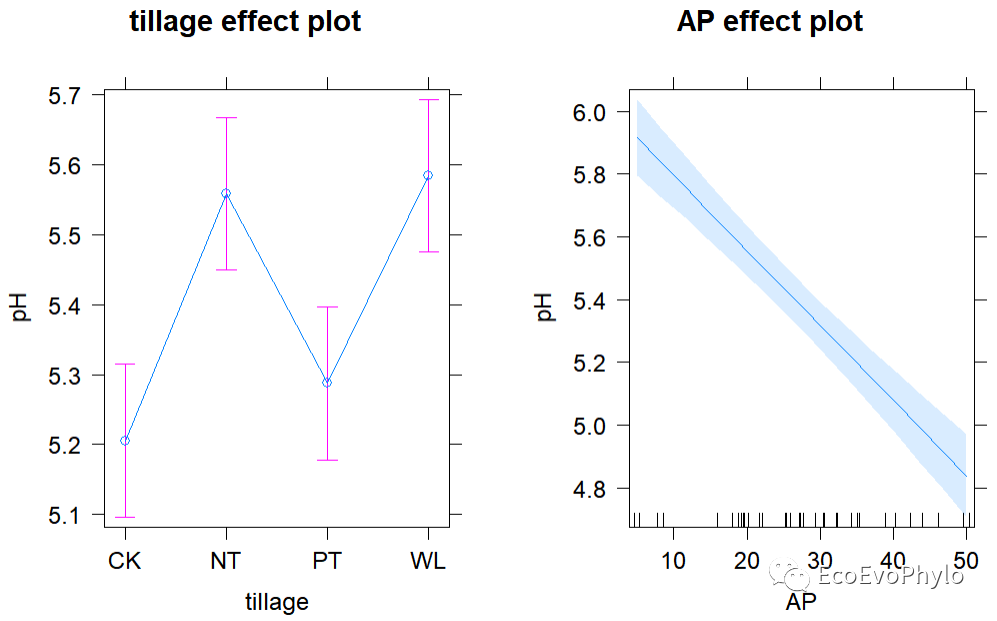
图36|模型固定效应预测效应图。AP效应图横轴上的小竖线表示数据点。

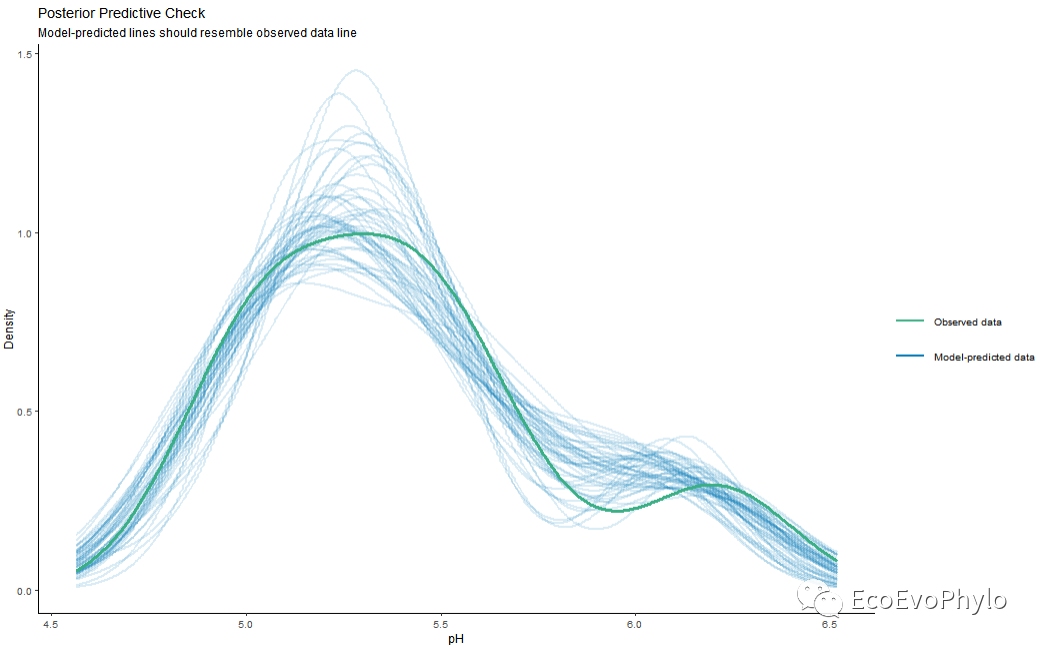
图37|模型预测效果图。


# 3.3.6 输出模型文字描述
report::report(fm1)

We fitted a linear mixed model (estimated using ML and nloptwrap optimizer) to predict pH with tillage and AP (formula: pH ~ tillage + AP). The model included depth as random effect (formula: ~1 | depth). The model's total explanatory power is substantial (conditional R2 =
0.88) and the part related to the fixed effects alone (marginal R2) is of 0.86. The model's intercept, corresponding to tillage = CK and AP = 0, is at 5.83 (95% CI [5.65, 6.01], t(29) = 67.05, p < .001). Within this model:

- The effect of tillage [NT] is statistically significant and positive (beta = 0.35, 95% CI [0.22, 0.49], t(29) = 5.42, p < .001; Std. beta = 0.88, 95% CI [0.55, 1.21])
- The effect of tillage [PT] is statistically non-significant and positive (beta = 0.08, 95% CI [-0.05, 0.22], t(29) = 1.25, p = 0.223; Std. beta = 0.20, 95% CI [-0.13, 0.54])
- The effect of tillage [WL] is statistically significant and positive (beta = 0.38, 95% CI [0.25, 0.51], t(29) = 6.04, p < .001; Std. beta = 0.94, 95% CI [0.62, 1.26])
- The effect of AP is statistically significant and negative (beta = -0.02, 95% CI [-0.03, -0.02], t(29) = -10.61, p < .001; Std. beta = -0.76, 95% CI [-0.91, -0.61])

Standardized parameters were obtained by fitting the model on a standardized version of the dataset. 95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation.

可参照此输出描述自己的结果。

3.4 随机斜率模型构建、检验及可视化

在文章中需要描述以下信息：1)模型描述(因变量、固定效应和随机效应)；2)数据是否满足线性混合模型假设；3)数据是否存在异常值及如何处理异常值；4)模型系数与模型检验结果；5)根据研究目的，有些还需要自变量的MarginalR2分解结果。

理论知识在随机截距模型部分已提及，此处用随机斜率模型演示如何快速得到上述结果。

此处因为fm1使用的ML法，为了方便后续比较，后续模型都使用的ML法，但是ML法可能会低估随机效应的方差，所以模型构建可优先选用REML法。特别当混合效应模型存在嵌套随机效应时，则不应该选用ML算法。


# 3.4.1 构建随机斜率模型
control <- lmerControl(
  optCtrl = list(
   algorithm = "NLOPT_LN_NELDERMEAD",
   xtol_abs = 1e-12,
   ftol_abs = 1e-12,
   check.conv.singular = .makeCC(action = "ignore", 
                                 tol = 1e-12)
  )
)
fm3 <- lmerTest::lmer(pH ~ tillage + AP + (1+tillage|depth), 
           data = env,
           REML = FALSE)
fm3.res <- fm3 %>% summary
fm3.res # 不是所有回归系数都显著。

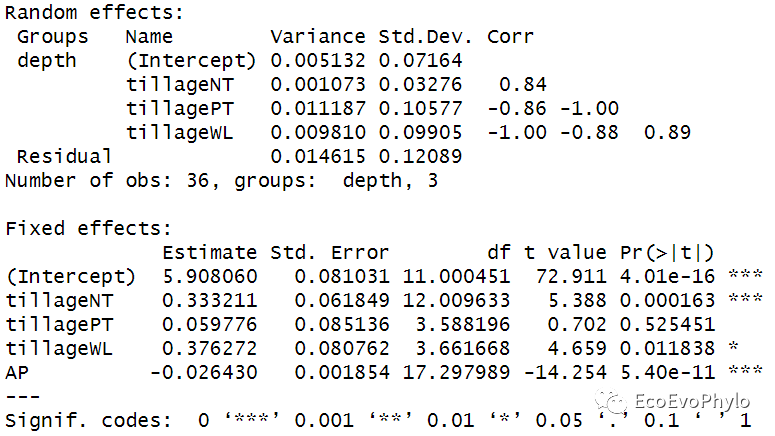
图38|随机斜率模型参数。随机斜率模型设置depth中pH的变化速度在tillage各水平不同，因此随机效应增加了三个随机斜率，tillageCK是对照组。结果中给出了随机斜率与随机截距的相关性，比较两者有比较高的相关性，一般比较好，但是如果非常接近1或−1就表示模型拟合有问题。


# 3.4.2 模型诊断-检验模型是否符合混合效应模型的假设及是否存在异常值。
theme_set(theme_classic(base_size = 6)) # windows太小，绘图会报错，先将ggplot2绘图的字体设置小一点。
pdf("fm3.check.model.pdf",width = unit(12,"cm"),height = unit(12,"cm"),family="Times")
(fmd3 <- performance::check_model(fm3))
dev.off()
fmd3$INFLUENTIAL #查看是否存在异常点。

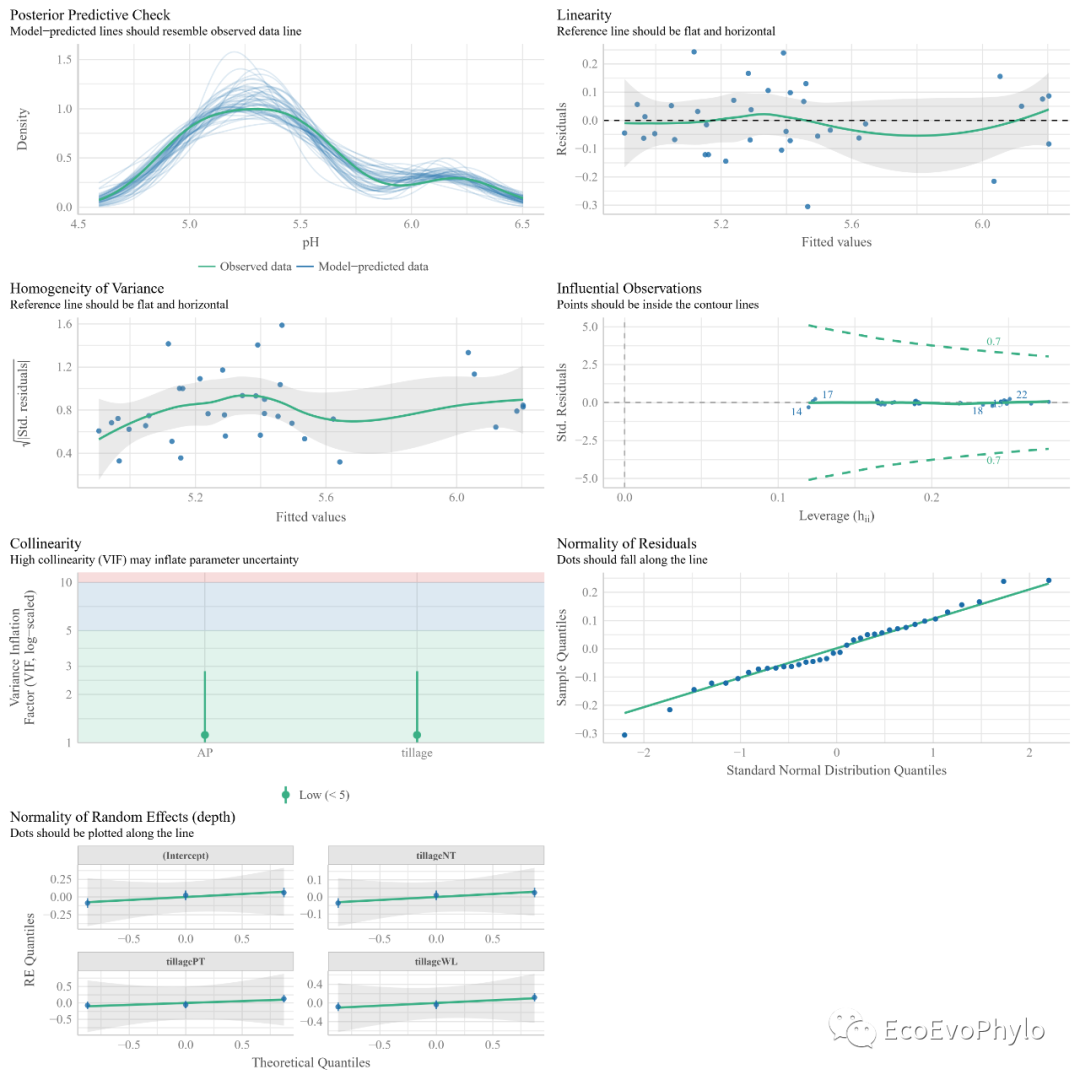
图39|随机斜率模型假设检验综合图。混合线性效应模型需要满足的假设，在图中标题处有注明。与随机截距模型不同的时，此处随机斜率模型增加了三个随机斜率。


# 3.4.3 模型检验
## 固定效应显著性检验-图表中有关Marginal R2/Conditional R2的计算，推荐替换为MuMIn::r.squaredGLMM()的计算结果。
### 随机效应输出的是标准误
options(modelsummary_get = "all")
(modelsummary::modelsummary(list("fm3" = fm3),
                            stars=TRUE,
                            estimate = "{estimate} ({std.error}){stars}", # 展示模型固定效应统计量、标准误和显著性标记。
                            statistic = "conf.int",# 展示置信区间。
                            output = "fm3.docx")) 
### 随机效应输出的 Variance，两个函数的输出可以综合起来，选择自己需要的。
(sjPlot::tab_model(fm3,
                  collapse.ci = TRUE,
                  p.style = "numeric_stars",
                  file="fm3.html")) 
## 随机效应检验
ranova(fm3)
## 模型整体固定效应检验
car::Anova(fm3) 
## 模型间比较
anova(fm1,fm3)

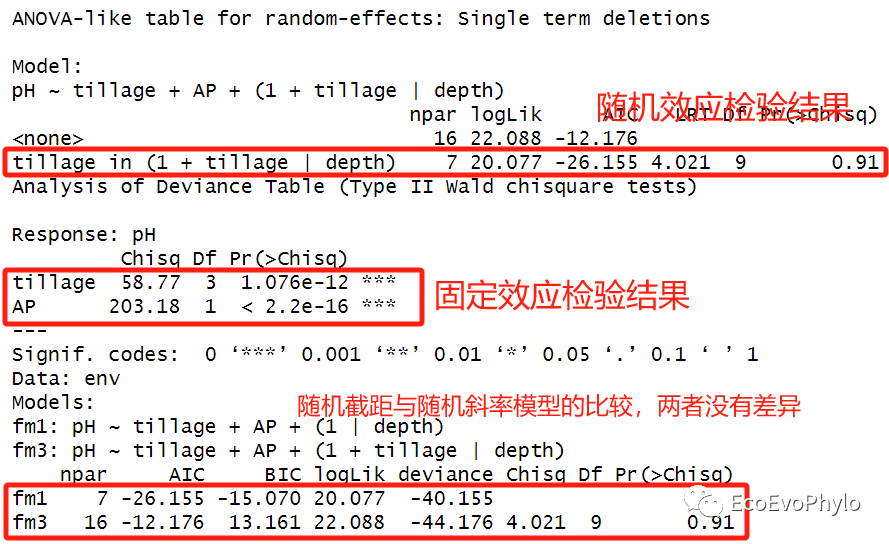
图40|随机斜率模型检验结果。随机效应检验结果显示，(1 + tillage | depth)项的LRT检验仍然不显著，即在此模型中pH在depth的初始值以及对tillage各水平的响应都没显著差异。不用执行随机斜率模型。模型anova检验结果显示tillage和AP固定因子对pH的影响还是显著的。


# 3.4.4 方差分解
## 推荐使用glmm.hp()进行方差分解
glmm.hp::glmm.hp(fm3)
glmm.hp::glmm.hp(fm3)$hierarchical.partitioning
## 方差分解结果绘图-详细绘图方式随机截距模型已经画过了，这里使用函数的默认绘图函数进行绘制。
plot(glmm.hp::glmm.hp(fm3))

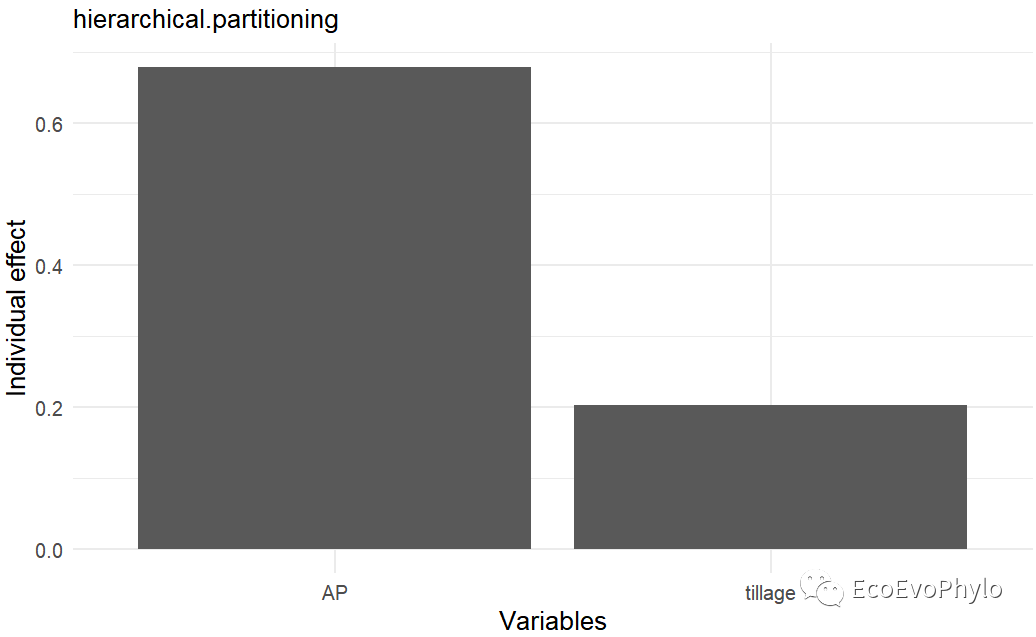
图41|随机斜率模型方差分解结果。模型固定效应的边际R2从~0.85到~0.88，提高的并不多，没必要进行随机斜率模型。


# 3.4.5 混合效应模型结果可视化
## 绘制随机效应水平间变化：绘制随机截距和斜率与模型总体截距和斜率的差异。
# lattice::dotplot(ranef(fm3, condVar=T))
library(sjPlot)
# browseVignettes("sjPlot") # 查看sjPlot包帮助文档，http://127.0.0.1:18066/session/Rvig.44ec3f8547bc.html。
(re.effects <- plot_model(fm3, type = "re", show.values = TRUE))

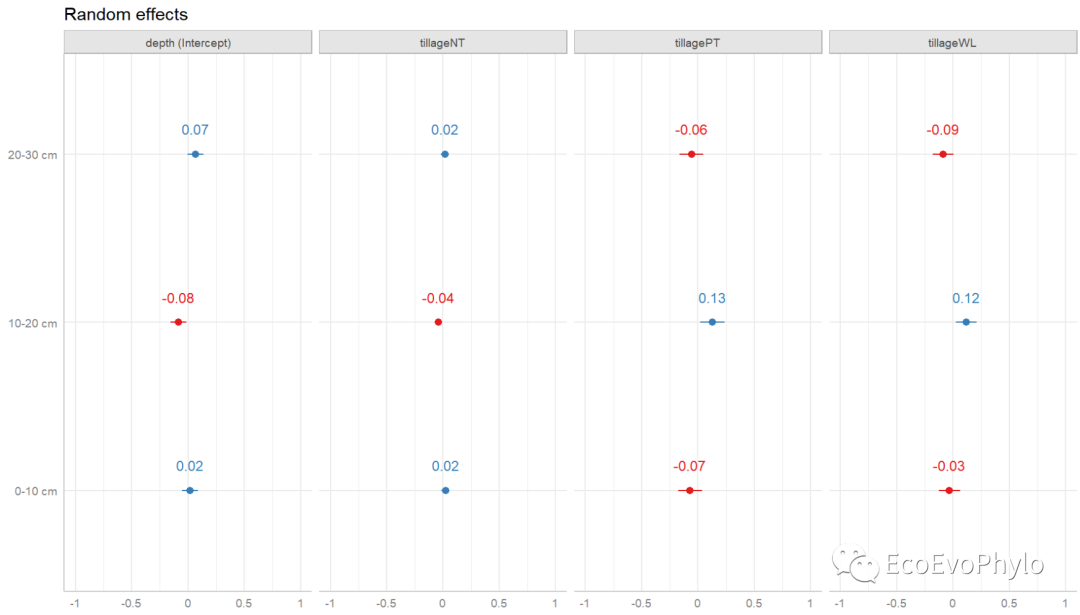
图42|绘制随机效应水平间变化。


## 绘制固定因子预测效应图。
# plot(effects::allEffects(fm3)) 
plot_model(fm3,type = "pred") # tillage与AP各一幅图。

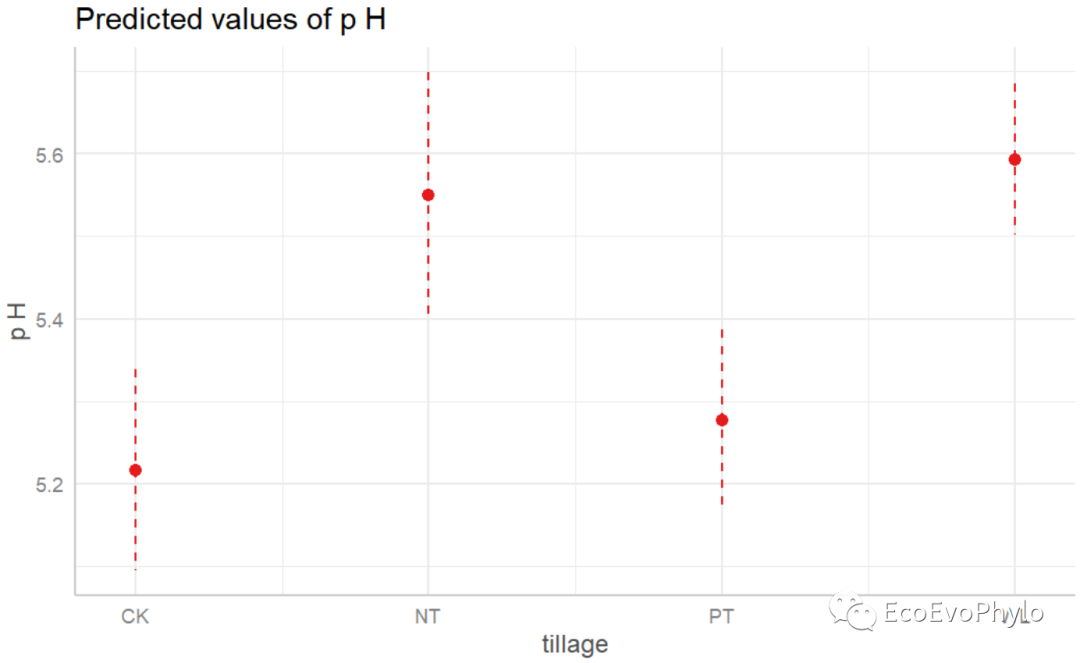
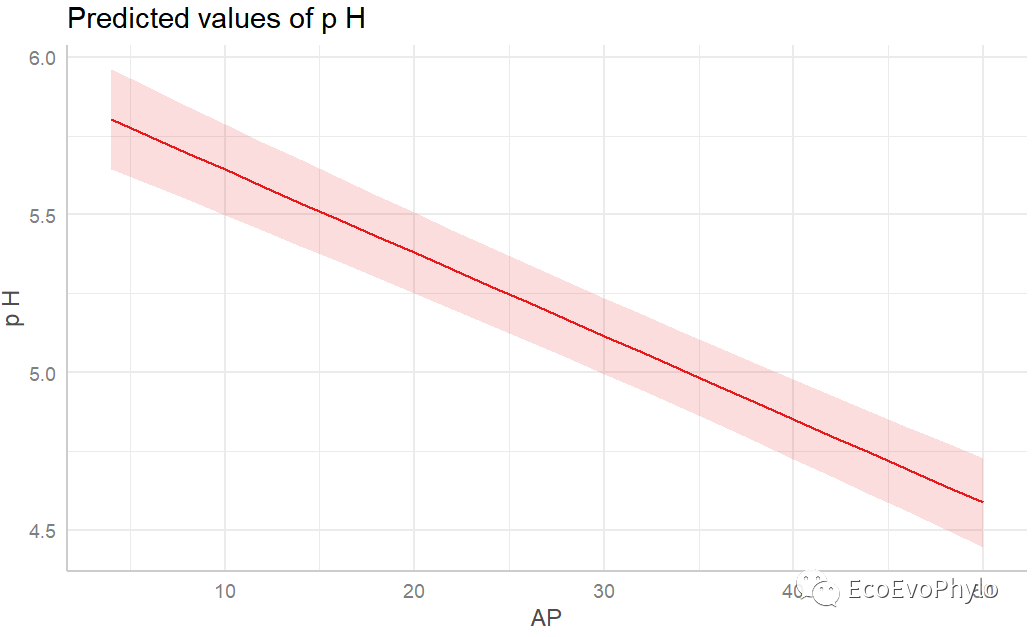
图43|固定因子预测效应图。


## 绘制固定效应系数图
plot_model(fm3,
           sort.est = TRUE,#按系数值大小排序。
           show.values = TRUE, # 显示系数值和显著性标签。
           value.offset = .3)

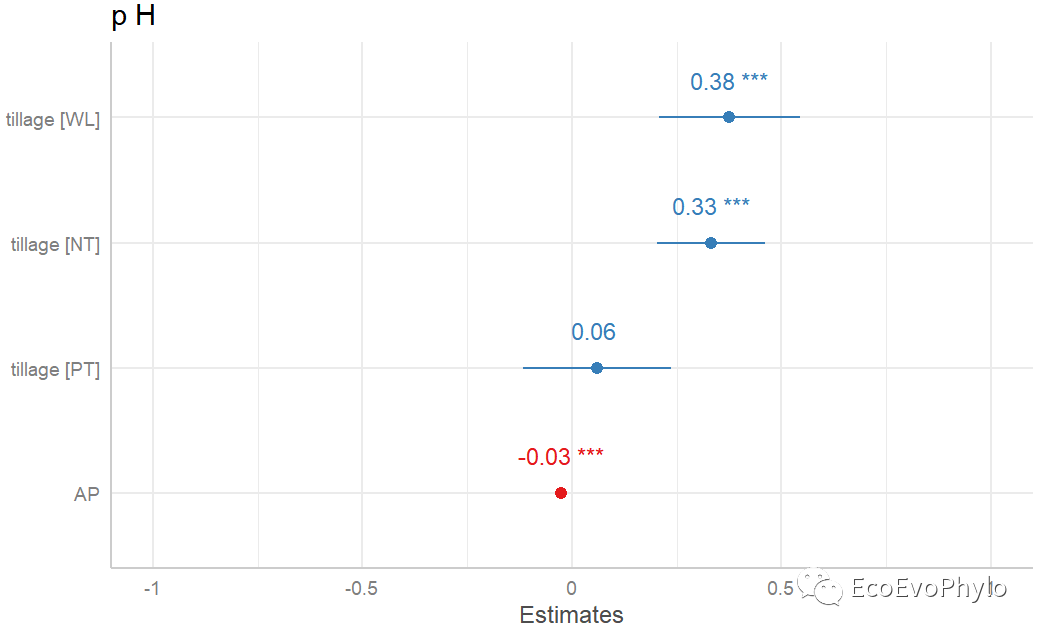
图44|固定效应系数图。


## 绘制模型预测效果图。
performance::check_predictions(fm3)

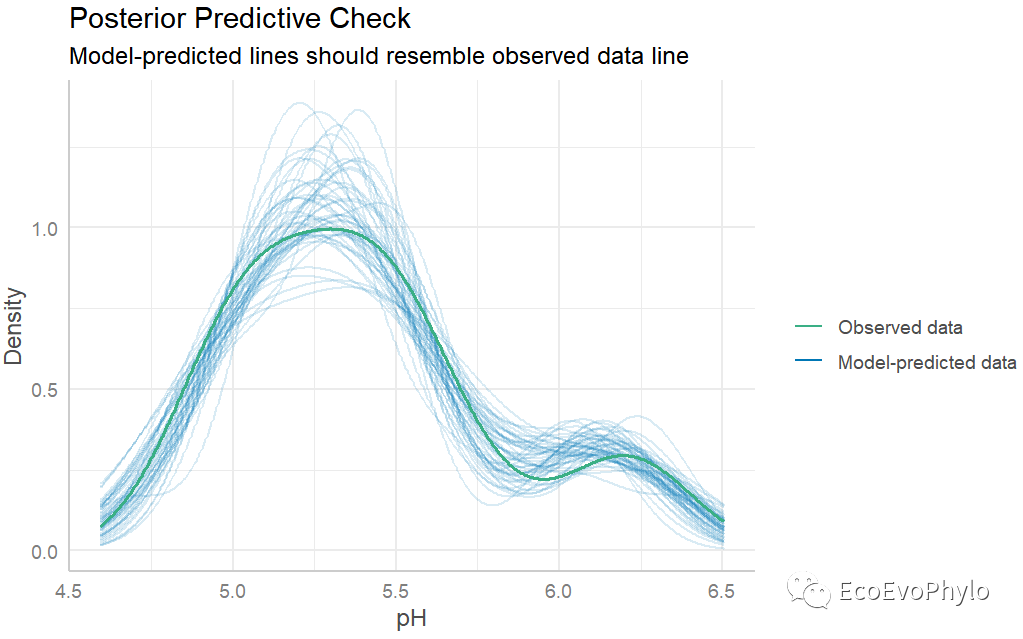
图45|模型预测效果图。


## 绘制随机斜率模型及置信区间
library(ggeffects)
### 提取estimated marginal means (predicted values)-与predict()的预测是不一样的。
fm3.pred <- ggpredict(
  fm3, 
  terms = c("AP","tillage","depth"), # 当连续自变量多于两个，就不好绘图了,就需要考虑分别绘图。
  type = "re",
  ci.lvl = 0.95
  ) 
fm3.pred
### 绘制随机效应
fm3.pred %>%
  plot() 
### plot_model也可选择自变量提取预测值并绘图
# plot_model(fm3,type = "pred",
#            terms = c("AP", "tillage", "depth")) # terms可以选择预测用自变量。

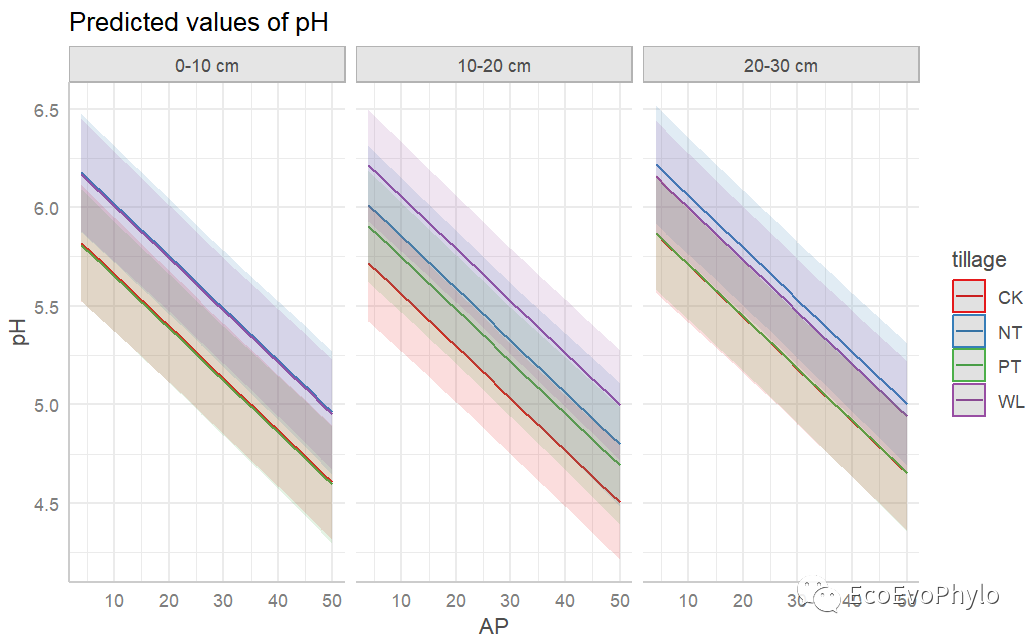
图46|随机斜率模型及置信区间。如图所示，depth个水平pH在tillage各水平的变化速度相似，没必要构建随机斜率模型。sjPlot是一个很强大的模型参数提取和绘图的包，可以参考帮助文档好好学习一下。


## ggplot2自定义绘图
### 固定效应+模型预测值绘图，查看模型预测效果。
(fm3_plot <- ggplot(env, aes(x = AP, y = pH, 
                             colour = tillage,
                             shape = depth)) +
      geom_point(alpha = 0.8,size = 3.5) +
      theme_bw() +
    scale_color_manual(values = ggsci::pal_aaas()(4))+
    scale_shape_manual(values = c(16,17,15))+
    scale_linetype_manual(values = c(1,2,4))+ # 设置depth对应不同线型。
      geom_line(
        data = cbind(env, pred = predict(fm3)), # 合并env与模型预测pH值。
        aes(y = pred,
            linetype = depth #可设置根据depth变化线型。
            ), linewidth = 0.75) +  # adding predicted line from mixed model 
    # facet_wrap(~depth,nrow = 1)+ # 也可根据depth绘制分面图。
      theme(legend.position = "right")  
)
ggsave("fm3.pred.pdf",fm3_plot,device = "pdf",family = "Times")
### 绘制混合效应模型预测图-可视化效果一般。
# (ggplot(fm3.pred) + 
#    geom_line(aes(x = x, y = predicted)) + # slope
#    geom_ribbon(aes(x = x, ymin = predicted - std.error, ymax = predicted + std.error), 
#                fill = "lightgrey", alpha = 0.5) +  # error band
#    geom_point(data = env,                      # adding the raw data (scaled values)
#               aes(x = AP, y = pH, colour = depth)) + 
#    theme_minimal()
# )

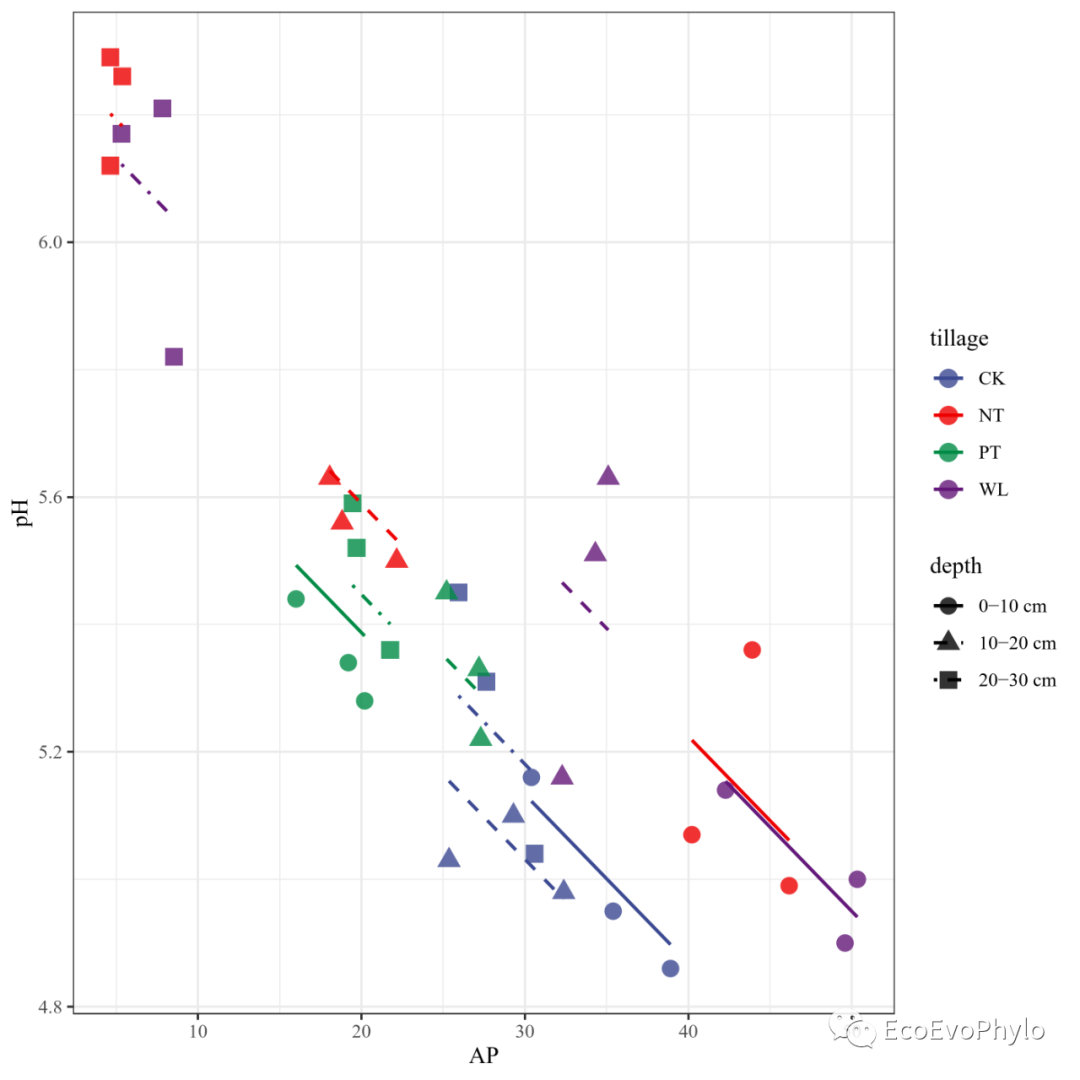
图47|随机斜率模型预测效果。可根据随机效应depth绘制分面图，图会更易读。


# 3.4.6 混合效应模型结果文字描述
report::report(fm3) #输出结果部分的marginal R2部分可以自己根据glmm.hp的结果修改。

We fitted a linear mixed model (estimated using ML and nloptwrap optimizer) to predict pH with tillage
and AP (formula: pH ~ tillage + AP). The model included tillage as random effects (formula: ~1 +
tillage | depth). The model's explanatory power related to the fixed effects alone (marginal R2) is
0.91. The model's intercept, corresponding to tillage = CK and AP = 0, is at 5.91 (95% CI [5.74,
6.08], t(20) = 72.91, p < .001). Within this model:

- The effect of tillage [NT] is statistically significant and positive (beta = 0.33, 95% CI [0.20,
0.46], t(20) = 5.39, p < .001; Std. beta = 0.83, 95% CI [0.51, 1.15])
- The effect of tillage [PT] is statistically non-significant and positive (beta = 0.06, 95% CI
[-0.12, 0.24], t(20) = 0.70, p = 0.491; Std. beta = 0.15, 95% CI [-0.29, 0.59])
- The effect of tillage [WL] is statistically significant and positive (beta = 0.38, 95% CI [0.21,
0.54], t(20) = 4.66, p < .001; Std. beta = 0.94, 95% CI [0.52, 1.36])
- The effect of AP is statistically significant and negative (beta = -0.03, 95% CI [-0.03, -0.02],
t(20) = -14.25, p < .001; Std. beta = -0.84, 95% CI [-0.96, -0.72])

Standardized parameters were obtained by fitting the model on a standardized version of the dataset.
95% Confidence Intervals (CIs) and p-values were computed using a Wald t-distribution approximation.

输出结果部分的marginal R2部分可以自己根据glmm.hp的结果修改。

四、线性混合效应模型选择

4.1 多模型比较

我们在3.1部分构建了多个线性混合效应模型，可以使用AIC、BIC、R2等模型评价参数对模型进行比较和差异显著性检验。


# 4.1.1 多个模型参数输出-直接根据模型的AIC、BIC和R2等值和固定效应显著性结果选择模型。
modelsummary::modelsummary(
  list(
    "fm1"=fm1,
    "fm2"=fm2,
    "fm3"=fm3,
    "fm4"=fm4,
    "fm5"=fm5,
    "fm6"=fm6,
    "fm7"=fm7,
    "fm8"=fm8
  ),
  # stars = TRUE,
  estimate= "{estimate} [{conf.low}, {conf.high}] {stars}",
  statistic =NULL,
  output = "multi-model.docx"
)

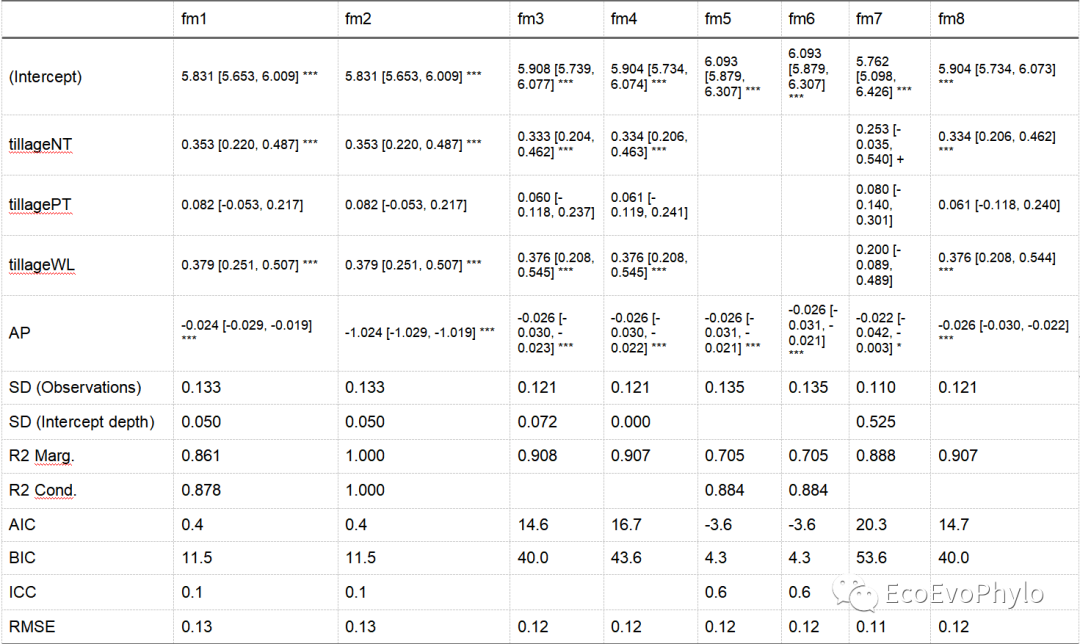
图48|多模型评估参数输出结果，multi-model.docx。图中只展示了部分内容，用于不同模型间比较。一般来说，AIC、BIC和RMSE值小些比较好，R2值大些比较好。但是所有模型都要考虑偏差-方差平衡，模型不能欠拟合也不能过拟合。根据自己的数据，选择合适的即可。


# 4.1.2 模型差异比较-复杂模型与简单模型相比。
## anova()根据AIC的Likelihood Ratio Test进行模型比较。
##固定效应或随机效应不同的模型anova都可比较。
##当多于2个模型时，模型顺序放置不同，输出的比较结果可能不一样。所以最好模型间都进行两两比较。
anova(fm3,fm1) 
anova(fm8,fm1)

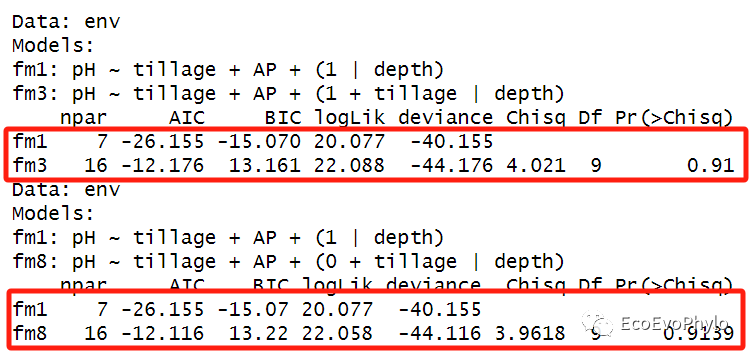
图49|LRT法模型比较结果。随机截距模型(fm1)与随机斜率模型(fm8),以及与随机斜率+随机截距模型(fm3)的差异都不显著。当多于2个模型时，模型顺序放置不同，输出的比较结果可能不一样，所以最好模型间都进行两两比较。或者使用Markov Chain Monte Carlo (MCMC) 或parametric bootstrap confidence intervals进行模型比较更好。当使用REML拟合混合效应模型时，REML 标准中的一项会随着固定效应结构的变化而变化，从而使得固定效应结构不同的模型之间的比较毫无意义。因此，如果要使用LRT 来评估固定效应不同的模型的显著性，则必须使用ML来拟合模型。


## 4.1.3 pbkrtest包进行Kenward-Roger approximation检验
##比较的模型必须是REML拟合模型，函数会对ML拟合模型重新进行REML拟合。
##实际使用时，发现仅能比较固定效应不同的模型。
library(pbkrtest)
fm9 <- update(fm1.1, .~. - AP)
(kr <- KRmodcomp(fm1.1, fm9)) #模型顺序依次为复杂模型，简单模型。
kr %>% summary
## 4.1.4 Satterthwaite approach
##实际使用时，发现仅能比较固定效应不同的模型。
(sa <- SATmodcomp(fm1.1, fm9))
sa %>% summary

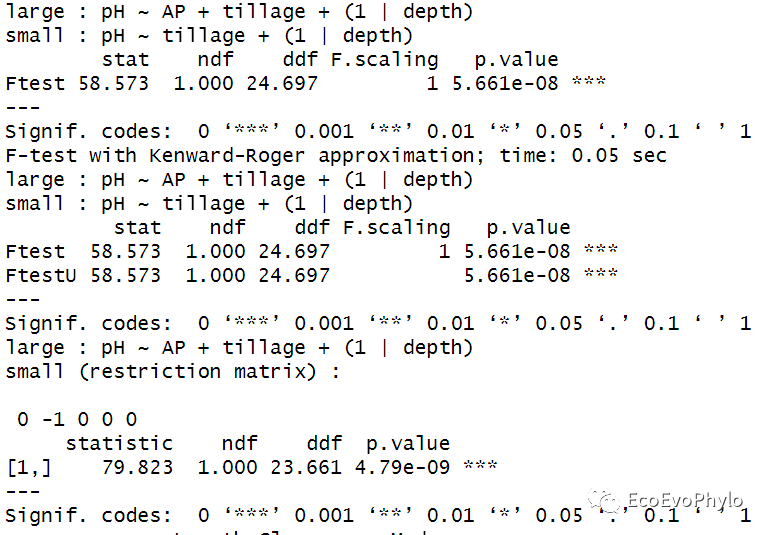
图50|固定效应不同模型的比较结果。Kenward-Roger approximation和Satterthwaite approach的检验结果都显示，复杂模型能更好的拟合数据。


## 4.1.5 Parametric bootstrap
##针对此数据集，对仅随机效应不同的模型的比较效果不好。
# PBmodcomp(fm1, fm3, nsim=500, cl=2) # fm1与fm3仅随机效应不同。
(pb <- PBmodcomp(fm1.1, fm9, nsim=500, cl=2))
pb %>% summary

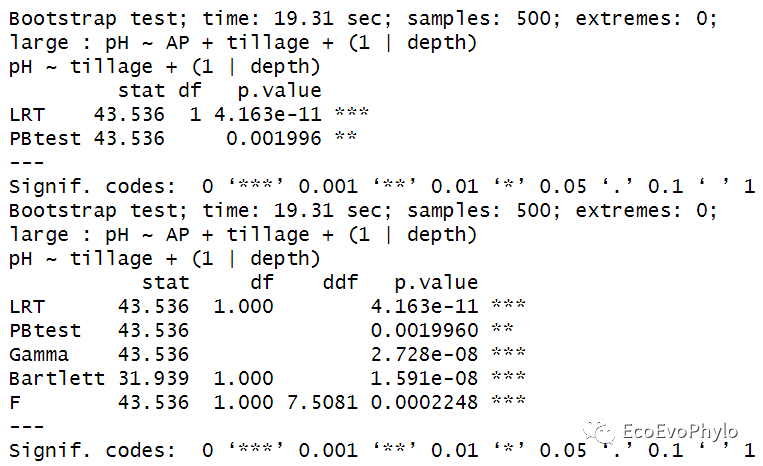
图51|固定效应不同的模型的Parametric bootstrap法比较结果。基于LRT的Parametric bootstrap检验结果也显示复杂模型能更好的拟合数据。

4.2 模型最优子集筛选

最优子集回归：算法使用所有可能的特征组合来拟合模型。分析者需要应用自己的判断和统计分析来选择最优模型。当特征数多于观测数时，这个方法的效果就不会好。

此处介绍如何使用MuMIn包进行最优子集回归，筛选特征，根据模型筛选准则筛选模型以及构建平均加权模型。


# 4.2.1 全模型构建
full <- lmer(pH ~ tillage + AP + TN + TP+ TK + Nitrate + Ammonia + AHN + AK + OM + OC + (1|depth), 
           data = env,
           REML = FALSE,
           na.action= "na.fail") # 此参数必须设置，否则后续会报错。
full %>% summary
# 4.2.2 生成具有全局模型中固定效应项的组合(子集)的模型的模型选择表，具有可选的模型包含规则。
dd <- MuMIn::dredge(
  # 全模型
  full,
  # 模型子集的排序基准。
  rank = "BIC", # 也可按照AIC排序
  # 回归系数标准化方法。
  beta = "partial.sd",
  # 设置输出的模型筛选指数。
  extra = alist(AIC, BIC, "R^2","adjR^2"),
  # 设置某变量包含在所有模型中。
  fixed = "AP",
  # 设置模型筛选方式,只输出包含AP的模型子集。
  subset = expression(AP)
                    )
dd %>%
  summary()


# 4.2.3 模型筛选方法一：提取最佳拟合模型，BIC值最低的模型。
fm_best <- MuMIn::get.models(dd, 1)[[1]]
fm_best %>%
  summary()

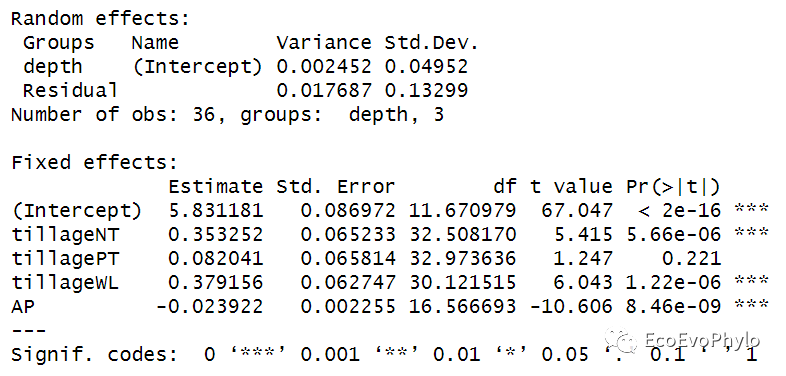
图52|根据BIC最小值筛选的最优子集随机截距模型。基于LRT的Parametric bootstrap检验结果也显示复杂模型能更好的拟合数据。BIC最小的模型就是随机截距模型fm1。如果设置REML=TRUE，输出的最佳模型仍然是随机截距模型fm1，但是就是固定效应和随机效应的检验值会有些差异，但是趋势是一致的。输出结果Estimate， Std. Error， t value, Pr(>|t|):依次表示对应固定效应的的回归系数及其标准误，回归系数检验的t检验统计量及其p值。分类因子作为自变量时，因子中的每个分类水平都会有一个回归系数，第一个分类水平作为哑变量，其回归系数为0。此模型中tillageCK的回归系数为0。

AICc指标可以纠正估计AIC时因样本量较小而产生的偏差。MuMIn包会计算delta AICc，还可以使用AICcmodavg包中的AICc函数来比较模型。一般来说，如果模型彼此相差在2个AICc单位(delta AICc)以内，则它们非常相似。在5个单位内，它们非常相似，相差超过10个单位，则AICc较低的模型拟合更好。利用MuMIn包dredge()生成所有自变量可能组合出的模型，并根据BIC排序。然后使用MuMIn::model.avg()利用模型平均的方法获得所有满足筛选条件的模型加权后的最优模型参数估计。


# 4.2.4 模型筛选方法二：平均加权模型，
## 生成所有模型统计量表-包含模型F检验结果
d2 <- MuMIn::dredge(
  full,
  # 设置模型包含的terms(回归系数)数目(截距除外)
  # (1,NA)表示模型中至少要有一个回归系数。
  m.lim = c(1, NA), 
  rank = "BIC",
  extra = list(
    "BIC","AIC","R^2",
    "*" = function(x) {
        s <- summary(x)
        c(Rsq = s$r.squared,
            F = s$fstatistic[[1]])
    })
)
d2 %>%
  summary()

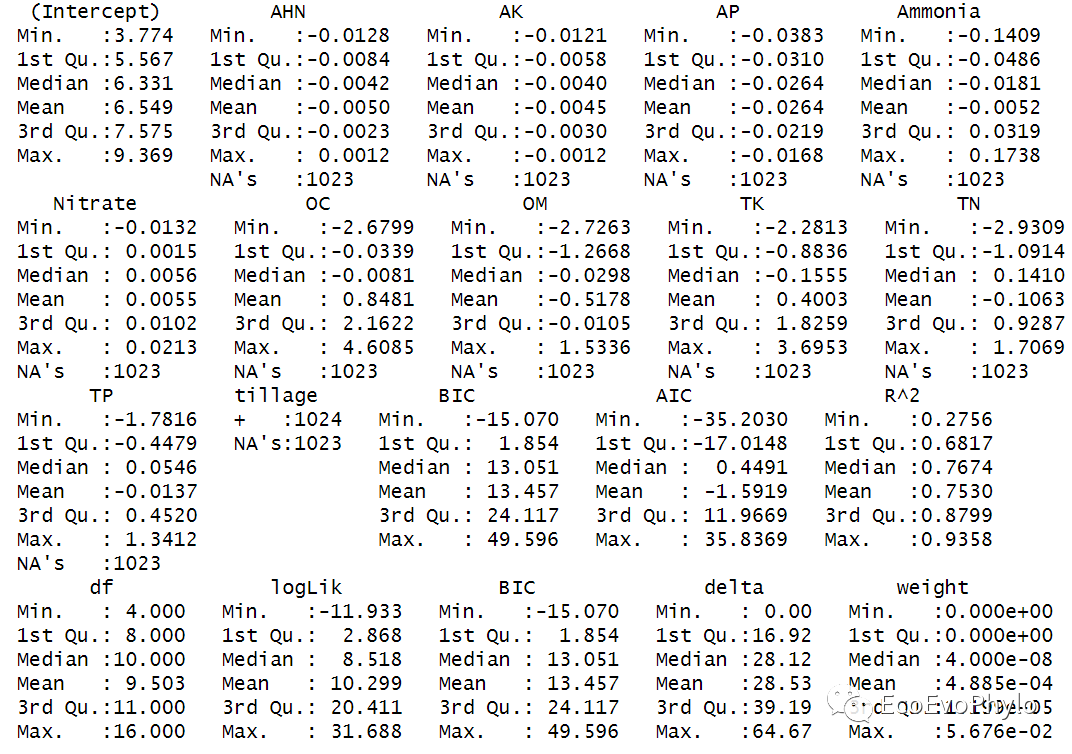
图53|多模型参数结果描述统计。


## 模型筛选方法二：模型平均加权获得最优模型
##根据delta AICc筛选模型:ΔAICc<2的模型被认为具有相同的优良性。
### 提取delta AICc<2的所有模型
fm_d2 <- MuMIn::get.models(d2, delta < 2)
# fm_d2 #输出结果是一个模型列表数据。
### 根据信息准则进行模型平均
##运行dredge()，未设置rank时，最好先使用get.models()提取模型，再传递给model.avg()，否则predict()等函数可能会对平均后模型不起作用。
##平均模型涉及因子变量时，需要注意，模型子集可能包含因子的不同分类，目前对此进行平均会产生毫无意义的结果。
fm_avg1 <- MuMIn::model.avg(
  fm_d2,
  beta = "partial.sd")
fm_avg1 %>%
  summary()

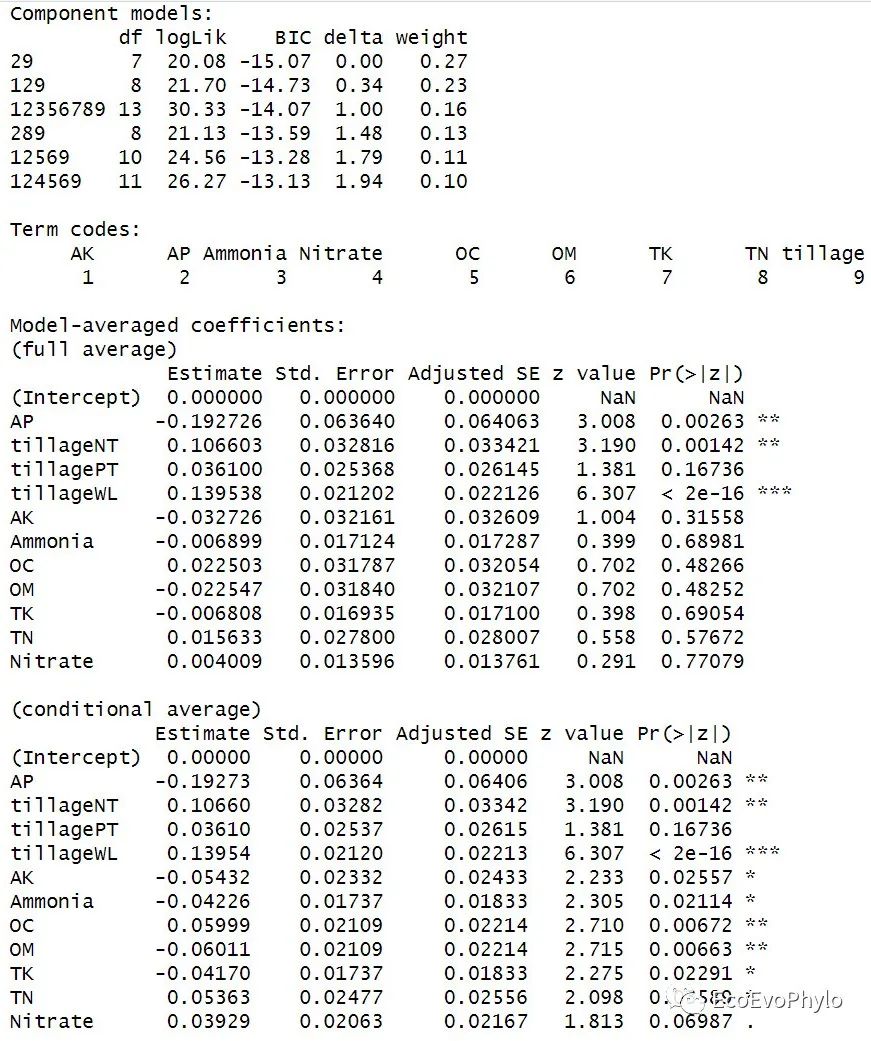
图54|将所有优良模型加权后的最优模型参数估计。平均加权模型中包含的模型子集以及"full"和““subset””平均模型的回归系数检验结果。平均模型系数：包含“full"和”subset”两种形式，‘subset’ (‘conditional’) 平均表示只平均该变量回归系数存在的模型。

模型比较最好在同类模型中进行，如，不要使用模型评价参数直接比较lm模型与lmm模型。当模型自变量较多需要进行筛选或想进行模型平均时，推荐使用MuMIn包进行最优子集筛选和模型平均。更详细教程可查看R统计绘图-多重线性回归(平均加权模型/最优子集筛选，MuMIn)。更多输出内容见LMM.html文件。

数据及代码文件：

链接：https://pan.baidu.com/s/1GkLdiziWhjH_K4GGTA75XQ?pwd=zkbr

提取码：zkbr

若链接失效，请在此文章下留言。代码以LMM.Rmd和LMM.html中为准。

参考资料：

《白话统计》

https://blog.csdn.net/WANMOUD/article/details/106114155

https://zhuanlan.zhihu.com/p/126706627

https://zhuanlan.zhihu.com/p/461859366

https://www.zhihu.com/question/370213292

https://zhuanlan.zhihu.com/p/345848835

资料地址：

https://link.springer.com/article/10.3758/s13428-016-0809-y

[lmer教程](https://cran.r-project.org/web/packages/multilevelTools/vignettes/lmer-vignette.html)

https://cran.r-project.org/web//packages/pbkrtest/vignettes/a01-pbkrtest.html

https://ourcodingclub.github.io/tutorials/mixed-models/?nsukey=JfcXN4ZtaaEgpYJMyxe3oLJVjnlrrISjyCNa8jr%2FJxC5boovrpcf%2BTJJhmqhALfQNznAP1VPeUUSZghPYi93AZHNXDFsaXoP9oL%2FEzSgzpmo9VmN7oUwmYExM%2F5cQ5Y3BhDFhWxHSxbAeT3iYd6fwXLzR65TQThi239DVAazfetJiUJlMdBoxgvfGykUcx50Fnd8BemyGv%2FLMezfhVe0tA%3D%3D&from=timeline

https://cran.r-project.org/web/packages/influence.ME/influence.ME.pdf

[混合模型的R2到底是如何计算的？](https://blog.sciencenet.cn/blog)

https://yury-zablotski.netlify.app/post/mixed-models/

https://library.virginia.edu/data/articles/correlation-of-fixed-effects-in-lme4

https://modelsummary.com/articles/modelsummary.html

[Multilevel Models using lmer](https://cran.r-project.org/web/packages/multilevelTools/vignettes/lmer-vignette.html)

https://rcompanion.org/handbook/G_03.html

https://www.r-bloggers.com/2016/06/simulation-and-power-analysis-of-generalized-linear-mixed-models/

https://tecdat.cn/%E5%A6%82%E4%BD%95%E8%A7%A3%E5%86%B3%E7%BA%BF%E6%80%A7%E6%B7%B7%E5%90%88%E6%A8%A1%E5%9E%8B%E4%B8%AD%E7%95%B8%E5%BD%A2%E6%8B%9F%E5%90%88singular-fit%E7%9A%84%E9%97%AE%E9%A2%98/

[R统计绘图-多重线性回归(平均加权模型/最优子集筛选，MuMIn)](https://mp.weixin.qq.com/s?__biz=MzIzMTgwMjk1NQ==&mid=2247486373&idx=2&sn=c9aab1c336b1ca82e4e05242bab23b10&chksm=e89fda81dfe853979fa22be257f03378ef12d5646634274895cdecc839bd50bd2a64d83a2357&scene=21#wechat_redirect)

R统计绘图-分子生态相关性网络分析(拓扑属性计算，ggraph绘图)

R统计绘图-变量分组相关性网络图(igraph)

机器学习-分类随机森林分析(randomForest模型构建、参数调优、特征变量筛选、模型评估和基础理论等)

R统计绘图-(O)PLS-DA分析(ropls)

R统计绘图-(O)PLS-DA分析(mixOmics)

机器学习-多元分类/回归决策树模型(rpart包)

R统计绘图-物种丰度差异检验及biomarker鉴定(LEfSe分析、ANOVA和K-W检验)

R统计绘图-LEfSe分析及可视化(microbiomeMarker)

R统计绘图-判别分析(LDA/QDA)

R统计绘图-分类变量相关性卡方检验及绘图

R统计绘图-多重线性回归(平均加权模型/最优子集筛选，MuMIn)

R统计绘图-多重线性回归(最优子集法特征筛选，leaps)