当网络退化时，浅层网络能够达到比深层网络更好的训练效果，这时如果我们把低层的特征传到高层，那么效果应该至少不比浅层的网络效果差，或者说如果一个VGG-100网络在第98层使用的是和VGG-16第14层一模一样的特征，那么VGG-100的效果应该会和VGG-16的效果相同。所以，我们可以在VGG-100的98层和14层之间添加一条直接映射（Identity Mapping）来达到此效果。

从信息论的角度讲，由于DPI（数据处理不等式）的存在，在前向传输的过程中，随着层数的加深，Feature Map包含的图像信息会逐层减少，而ResNet的直接映射的加入，保证了 l+1 层的网络一定比 l 层包含更多的图像信息。基于这种使用直接映射来连接网络不同层直接的思想，残差网络应运而生。

残差网络

残差块

残差网络是由一系列残差块组成的（图1）。一个残差块可以用表示为：

2 残差网络

残差网络的搭建分为两步：

使用VGG公式搭建Plain VGG网络
在Plain VGG的卷积网络之间插入Identity Mapping，注意需要升维或者降维的时候加入 1×1 卷积。

在实现过程中，一般是直接stack残差块的方式。

为什么叫残差网络

一、背景

1）梯度消失问题

我们发现很深的网络层，由于参数初始化一般更靠近0，这样在训练的过程中更新浅层网络的参数时，很容易随着网络的深入而导致梯度消失，浅层的参数无法更新。

解释：

可以看到，假设现在需要更新b1，w2,w3,w4参数因为随机初始化偏向于0，通过链式求导我们会发现，w1w2w3相乘会得到更加接近于0的数，那么所求的这个b1的梯度就接近于0，也就产生了梯度消失的现象。

2）网络退化问题

举个例子，假设已经有了一个最优化的网络结构，是18层。当我们设计网络结构的时候，我们并不知道具体多少层次的网络是最优化的网络结构，假设设计了34层网络结构。那么多出来的16层其实是冗余的，我们希望训练网络的过程中，模型能够自己训练这五层为恒等映射，也就是经过这层时的输入与输出完全一样。但是往往模型很难将这16层恒等映射的参数学习正确，那么就一定会不比最优化的18层网络结构性能好，这就是随着网络深度增加，模型会产生退化现象。它不是由过拟合产生的，而是由冗余的网络层学习了不是恒等映射的参数造成的。

二、ResNets 残差网络

ResNet使用了一个新的思想，ResNet的思想是假设我们涉及一个网络层，存在最优化的网络层次，那么往往我们设计的深层次网络是有很多网络层为冗余层的。那么我们希望这些冗余层能够完成恒等映射，保证经过该恒等层的输入和输出完全相同。具体哪些层是恒等层，这个会有网络训练的时候自己判断出来。

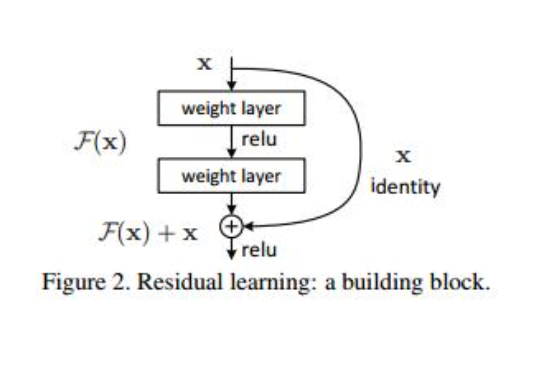
残差网络有什么好处呢？显而易见：因为增加了 x 项，那么该网络求 x 的偏导的时候，多了一项常数 1（对x的求导为1），所以反向传播过程，梯度连乘，也不会造成梯度消失。

可以看到X是这一层残差块的输入，也称作F(x)为残差，x为输入值，F（X）是经过第一层线性变化并激活后的输出，该图表示在残差网络中，第二层进行线性变化之后激活之前，F(x)加入了这一层输入值X，然后再进行激活后输出。在第二层输出值激活前加入X，这条路径称作shortcut连接。

三、网络架构

1）普通网络(Plain Network)

2) 残差网络

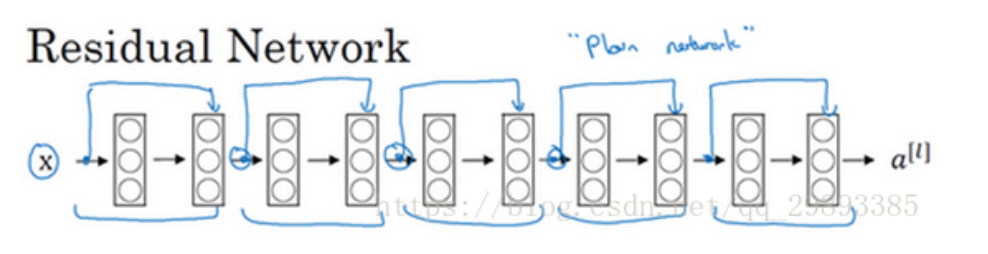
把它变成ResNet的方法是加上所有跳跃连接，每两层增加一个捷径，构成一个残差块。如图所示，5个残差块连接在一起构成一个残差网络。

3）对比分析

　　如果我们使用标准优化算法训练一个普通网络，比如说梯度下降法，或者其它热门的优化算法。如果没有残差，没有这些捷径或者跳跃连接，凭经验你会发现随着网络深度的加深，训练错误会先减少，然后增多。而理论上，随着网络深度的加深，应该训练得越来越好才对。也就是说，理论上网络深度越深越好。但实际上，如果没有残差网络，对于一个普通网络来说，深度越深意味着用优化算法越难训练。实际上，随着网络深度的加深，训练错误会越来越多。

但有了ResNets就不一样了，即使网络再深，训练的表现却不错，比如说训练误差减少，就算是训练深达100层的网络也不例外。有人甚至在1000多层的神经网络中做过实验，这样就让我们在训练更深网络的同时，又能保证良好的性能。也许从另外一个角度来看，随着网络越深，网络连接会变得臃肿，但是ResNet确实在训练深度网络方面非常有效。

四、解决问题

1）为什么可以解决梯度消失？

ResNet最终更新某一个节点的参数时，由于h(x)=F(x)+x，使得链式求导后的结果如图所示，不管括号内右边部分的求导参数有多小，因为左边的1的存在，并且将原来的链式求导中的连乘变成了连加状态，都能保证该节点参数更新不会发生梯度消失或梯度爆炸现象。

2）为什么可以解决网络退化问题？

我们发现，假设该层是冗余的，在引入ResNet之前，我们想让该层学习到的参数能够满足h(x)=x，即输入是x，经过该冗余层后，输出仍然为x。但是可以看见，要想学习h(x)=x恒等映射时的这层参数时比较困难的。ResNet想到避免去学习该层恒等映射的参数，使用了如上图的结构，让h(x)=F(x)+x;这里的F(x)我们称作残差项，我们发现，要想让该冗余层能够恒等映射，我们只需要学习F(x)=0。学习F(x)=0比学习h(x)=x要简单，因为一般每层网络中的参数初始化偏向于0，这样在相比于更新该网络层的参数来学习h(x)=x，该冗余层学习F(x)=0的更新参数能够更快收敛，如图所示：

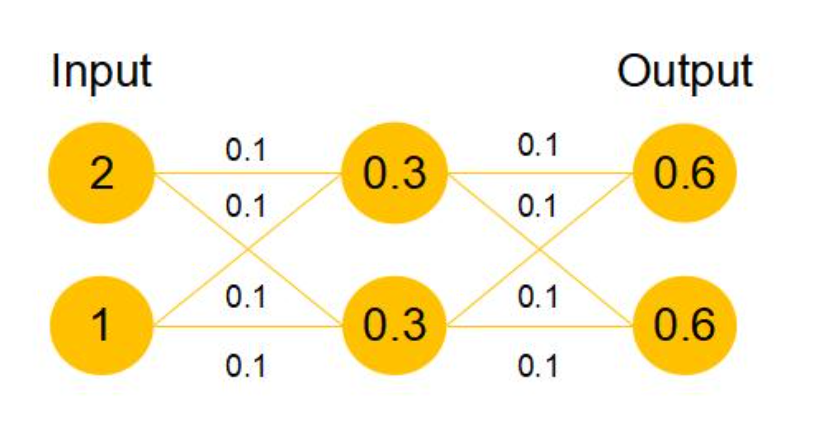
假设该曾网络只经过线性变换，没有bias也没有激活函数。我们发现因为随机初始化权重一般偏向于0，那么经过该网络的输出值为[0.6 0.6]，很明显会更接近与[0 0]，而不是[2 1]，相比与学习h(x)=x，模型要更快到学习F(x)=0。并且ReLU能够将负数激活为0，过滤了负数的线性变化，也能够更快的使得F(x)=0。这样当网络自己决定哪些网络层为冗余层时，使用ResNet的网络很大程度上解决了学习恒等映射的问题，用学习残差F(x)=0更新该冗余层的参数来代替学习h(x)=x更新冗余层的参数。

这样当网络自行决定了哪些层为冗余层后，通过学习残差F(x)=0来让该层网络恒等映射上一层的输入，使得有了这些冗余层的网络效果与没有这些冗余层的网络效果相同，这样很大程度上解决了网络的退化问题

原文：残差网络(Residual Network) - 光彩照人 - 博客园

详解残差网络 - 知乎

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/358798?site