RWKV 语言模型：具有 Transformer 优点的 RNN

RWKV 语言模型，这是一个具有巨大潜力的开源大型语言模型。由于 ChatGPT 和一般的大型语言模型最近受到了很多关注。在这篇文章中，我将尝试解释与大多数语言模型（transformer）相比，RWKV 有何特别之处。

RWKV 可视化 浅谈outlier 对LLM的影响…
RWKV-LM项目地址
ChatRWKV 聊天项目地址
WebUi-ChatRWKV 项目地址
discord 加入此项目
首先 先解释一下模型为何叫RWKV(作者本人BO哥自己说的)

• 模型最核心的机制 是RWKV 因为没有使用注意力 而类似注意力的东西叫做WKV
• SEO 独特些排名靠前

RWKV 模型是一种巧妙的 RNN 架构，使其能够像transformer一样进行训练。所以要解释RWKV，我需要先解释一下RNNs和transformers。

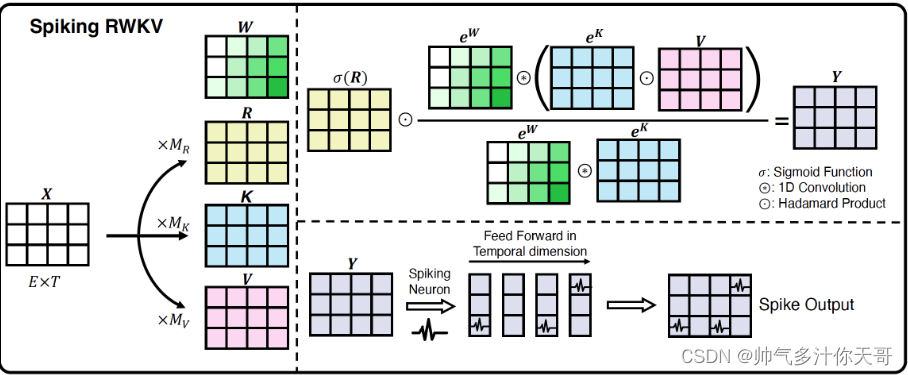
RNN 循环神经网络

传统上，用于序列（如文本）处理的神经网络是 RNN（如 LSTM）。RNN 接受两个输入：State和Token。它一次通过输入序列一个Token，每个Token更新状态。例如，我们可以使用 RNN 将文本处理成单个状态向量。然后，这可用于将文本分类为“正面”或“负面”。或者我们可以使用最终状态来预测下一个Token，这就是 RNN 用于生成文本的方式。

Transformer

由于 RNN 的顺序性质，它们很难在多个 GPU 上大规模并行化。这激发了使用“注意力”机制而不是顺序处理的动机，从而产生了一种称为Transformer的架构。Transformer同时处理所有Token，将每个Token与所有先前的Token并行比较。具体来说，注意力为每个Token计算“key”, “value” and “query”向量，然后使用这些计算所有Token对之间的权值。

除了能够通过大规模并行化加速训练之外，大型 Transformer 在基准测试中的得分通常优于 RNN。

然而，注意机制与要处理的序列的长度呈二次方关系。这有效地限制了模型的输入大小（或“上下文长度”）。此外，由于注意力机制，在生成文本时，我们需要在内存中保留所有先前Token的注意力向量。这比只存储单个状态的 RNN 需要更多的内存。

RWKV

RWKV 结合了 RNN 和 Transformer 的最佳特性。在训练期间，我们使用架构的Transformer类型公式，它允许大规模并行化（具有一种与Token数量线性扩展的注意力）。对于推理，我们使用等效的公式，它的工作方式类似于具有状态的 RNN。这使我们能够两全其美。

所以我们基本上有一个像Transformer 一样训练的模型，除了长上下文长度并不昂贵。在推理过程中，我们需要的内存要少得多，并且可以隐式处理“无限”上下文长度（尽管在实践中，模型可能很难泛化到比训练期间看到的上下文长度长得多的上下文长度）。

好的，但是性能呢？由于 RWKV 是 RNN，因此很自然地认为它在基准测试中的表现不如 transformer。此外，这听起来像是线性注意力。许多以前的线性时间注意力Transformer架构（如“Linformer”、“Nystromformer”、“Longformer”、“Performer”）似乎都没有SOTA。

性能

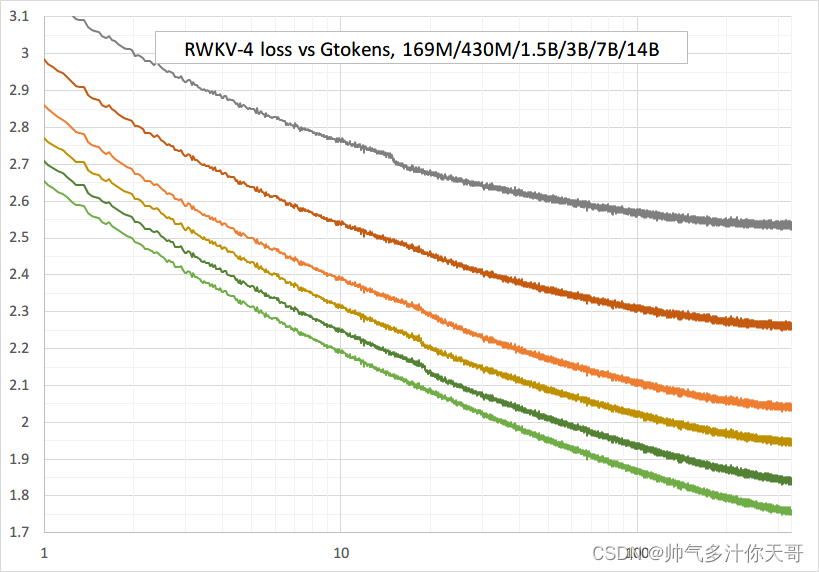
RWKV 似乎可以像 SOTA transformer一样缩放。至少多达140亿个参数。

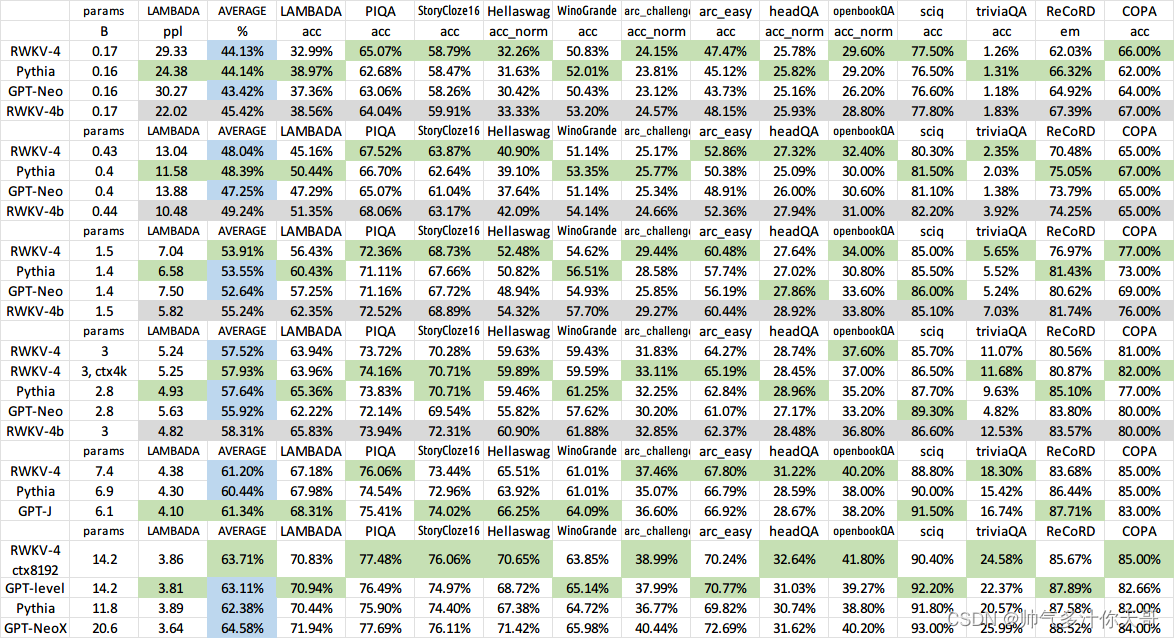
大型语言模型的成本估算

当查看 RWKV 14B（140 亿个参数）时，很容易问当我们像 GPT-3 一样扩展到 175B 时会发生什么。但是，训练 175B 模型的成本很高。计算类似 transformer 架构的近似训练成本实际上很简单。

对于每个输入标记，训练的瓶颈本质上是乘以所有参数，然后将其相加。通过自动微分，我们可以用大约另外 2 倍计算梯度，每个标记每个参数总共 6 个 FLOP。因此，在 3000 亿个Token上训练的 14B 模型大约需要14B×300B×6=2.5×1022 FLOPs。我们使用 A100 GPU 进行训练。使用 16 位浮点数，A100 理论上可以达到 312 TFLOPS，或者大约每小时 FLOPs。所以我们理论上至少需要22436小时的A100时间来训练。实际上，RWKV 14B 在 64 个 A100 上并行训练，出于各种原因牺牲了一点性能。RWKV 14B 耗时约 3 个月训练 100 小时，从而实现约 20% 的理论效率（因为它比理论最小值花费了大约 5 倍的时间）。最近的版本可以以大约 50% 的理论效率训练 RWKV 14B。

作为粗略的价格估算，在撰写本文时，cloud-gpus.com 上最便宜的 A100 成本为 0.79 美元/小时。因此，在那里训练最初的 14B RWKV 将花费大约 10 万美元，但随着最近训练代码的改进，我们可以将其减少到 4 万美元。实际上，还有其他考虑因素，如易用性、超时、多 GPU 通信速度等。因此，人们可能需要更多高端选项，如 AWS，每小时 4.096 美元。RWKV 接受了 Stability 和 EleutherAI 捐赠的计算训练。

现在你可以想象，训练 10 倍以上的参数和 10 倍以上的数据将花费 100 倍以上，使其变得非常昂贵。

RWKV 语言模型的工作原理

要准确解释 RWKV 的工作原理，我认为最简单的方法是查看它的简单实现。以下约 100 行代码（150RWKV_in_150_lines）是生成文本的相对较小（430m 参数）RWKV 模型的最小实现。

最小 RWKV 代码

import numpy as np
from torch import load as torch_load  # Only for loading the model weights
from tokenizers import Tokenizer

layer_norm = lambda x, w, b : (x - np.mean(x)) / np.std(x) * w + b
exp = np.exp
sigmoid = lambda x : 1/(1 + exp(-x))

def time_mixing(x, last_x, last_num, last_den, decay, bonus, mix_k, mix_v, mix_r, Wk, Wv, Wr, Wout):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    v = Wv @ ( x * mix_v + last_x * (1 - mix_v) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )

    wkv = (last_num + exp(bonus + k) * v) /      \
          (last_den + exp(bonus + k))
    rwkv = sigmoid(r) * wkv

    num = exp(-exp(decay)) * last_num + exp(k) * v
    den = exp(-exp(decay)) * last_den + exp(k)

    return Wout @ rwkv, (x,num,den)


def channel_mixing(x, last_x, mix_k, mix_r, Wk, Wr, Wv):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )
    vk = Wv @ np.maximum(k, 0)**2
    return sigmoid(r) * vk, x


def RWKV(model, token, state):
    params = lambda prefix : [model[key] for key in model.keys() if key.startswith(prefix)]

    x = params('emb')[0][token]
    x = layer_norm(x, *params('blocks.0.ln0'))

    for i in range(N_LAYER):
        x_ = layer_norm(x, *params(f'blocks.{i}.ln1'))
        dx, state[i][:3] = time_mixing(x_, *state[i][:3], *params(f'blocks.{i}.att'))
        x = x + dx

        x_ = layer_norm(x, *params(f'blocks.{i}.ln2'))
        dx, state[i][3] = channel_mixing(x_, state[i][3], *params(f'blocks.{i}.ffn'))
        x = x + dx

    x = layer_norm(x, *params('ln_out'))
    x = params('head')[0] @ x

    e_x = exp(x-np.max(x))
    probs = e_x / e_x.sum() # Softmax of x

    return probs, state

##########################################################################################################

def sample_probs(probs, temperature=1.0, top_p=0.85):
    sorted_probs = np.sort(probs)[::-1]
    cumulative_probs = np.cumsum(sorted_probs)
    cutoff = sorted_probs[np.argmax(cumulative_probs > top_p)]
    probs[probs < cutoff] = 0
    probs = probs**(1/temperature)
    return np.random.choice(a=len(probs), p=probs/np.sum(probs))


# Available at https://huggingface.co/BlinkDL/rwkv-4-pile-430m/resolve/main/RWKV-4-Pile-430M-20220808-8066.pth
MODEL_FILE = '/data/rwkv/RWKV-4-Pile-430M-20220808-8066.pth'
N_LAYER = 24
N_EMBD = 1024

print(f'\nLoading {MODEL_FILE}')
weights = torch_load(MODEL_FILE, map_location='cpu')
for k in weights.keys():
    if '.time_' in k: weights[k] = weights[k].squeeze()
    weights[k] = weights[k].float().numpy() # convert to f32 type


# Available at https://github.com/BlinkDL/ChatRWKV/blob/main/20B_tokenizer.json
tokenizer = Tokenizer.from_file("/data/rwkv/20B_tokenizer.json")

print(f'\nPreprocessing context')

context = "\nIn a shocking finding, scientist discovered a herd of dragons living in a remote, previously unexplored valley, in Tibet. Even more surprising to the researchers was the fact that the dragons spoke perfect Chinese."

state = np.zeros((N_LAYER, 4, N_EMBD), dtype=np.float32)
for token in tokenizer.encode(context).ids:
    probs, state = RWKV(weights, token, state)

print(context, end="")
for i in range(100):
    token = sample_probs(probs)
    print(tokenizer.decode([token]), end="", flush=True)
    probs, state = RWKV(weights, token, state)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

为了避免隐藏复杂性，模型计算本身完全用 python 编写，使用 numpy 进行矩阵/向量运算。但是，我需要使用它torch.load从文件中加载模型权重，并将tokenizers.Tokenizer文本转换为模型可以使用的标记。

使用 RWKV 生成文本

代码使用RWKV接续下面的文字：

In a shocking finding, scientist discovered a herd of dragons living in a remote, previously unexplored valley, in Tibet. Even more surprising to the researchers was the fact that the dragons spoke perfect Chinese.

我们首先需要将此文本转换为一系列标记（从 0 到 50276 的数字代表我们词汇表中的单词/符号/标记）。这不是这篇博文的重点，所以我只是用一个外部库来做tokenizer.encode(context).ids。

接下来，我们需要将这个Token序列处理成 RWKV 状态。本质上，RWKV 代表一个函数，它接受一个标记和一个状态，并输出下一个标记和新状态的概率分布。当然，该函数还取决于 RWKV 模型参数，但由于我们使用经过训练的模型（从此处下载），我们将这些参数视为固定的。要将文本转换为状态，我们只需将状态初始化为全零，然后通过 RWKV 函数将标记一个一个地输入。

state = np.zeros((N_LAYER, 4, N_EMBD), dtype=np.float32)
for token in tokenizer.encode(context).ids:
    probs, state = RWKV(weights, token, state)
1
2
3

现在变量state包含我们输入文本的状态表示，变量“probs”包含模型预测下一个标记的概率分布。

我们现在可以简单地对概率分布进行采样（实际上，我们避免在 中使用低概率标记sample_probs()）并向文本添加另一个标记。然后我们将新Token输入 RWKV 并重复。

for i in range(100):
    token = sample_probs(probs)
    print(tokenizer.decode([token]), end="", flush=True)
    probs, state = RWKV(weights, token, state)     
1
2
3
4

一个典型的生成的例子是：

“

They’re just like us. They use Tibetan for communication, and for a different reason – they use a language that they’re afraid to use. To protect their secret, they prefer to speak a different language to the local public.

当然，更大的模型会比这个相对较小的 430m RWKV 表现更好。

RWKV() 内部发生了什么

RWKV 做的第一件事是查找输入标记的嵌入向量。即x = params('emb')[0][token]。这里params('emb')[0]只是一个矩阵，然后我们提取一行。

下一行x = layer_norm(x, *params('blocks.0.ln0'))要求我解释什么是层归一化。最简单的方法是只显示定义：layer_norm = lambda x, w, b : (x - np.mean(x)) / np.std(x) * w + b.

直觉是它将向量 x 归一化为零均值和单位方差，然后对其进行缩放和偏移。请注意，scale w和 offset b是 1024 维向量，它们是学习到的模型参数。

现在我们进入模型的主要部分。分为 24 层，按顺序应用。

for i in range(N_LAYER):
    x_ = layer_norm(x, *params(f'blocks.{i}.ln1'))
    dx, state[i][:3] = time_mixing(x_, *state[i][:3], *params(f'blocks.{i}.att'))
    x = x + dx

    x_ = layer_norm(x, *params(f'blocks.{i}.ln2'))
    dx, state[i][3] = channel_mixing(x_, state[i][3], *params(f'blocks.{i}.ffn'))
    x = x + dx
1
2
3
4
5
6
7
8

请注意，我们只是向x 添加更新x = x + dx，这称为使用“residual connections”。每次我们深复制x，我们都会在混合之前对其进行层归一化处理。每层有两个混合功能：“时间混合”(time mixing)部分和“通道混合”(channel mixing)部分。在一个典型的变压器中，“时间混合”将由多头注意力完成，而“通道混合”将由一个简单的前馈网络完成。RWKV 做了一些不同的事情，我们将在下一节中解释。

Channel mixing 通道混合

我将从通道混合开始，因为它是两种混合功能中较简单的一种。

def channel_mixing(x, last_x, mix_k, mix_r, Wk, Wr, Wv):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )
    vk = Wv @ np.maximum(k, 0)**2
    return sigmoid(r) * vk, x
1
2
3
4
5

x通道混合层接受与此标记对应的输入，以及x与前一个标记对应的输入，我们称之为last_x。last_x存储在这个 RWKV 层的state. 其余输入是学习RWKV 的 parameters。

首先，我们使用学习的权重对x和进行线性插值last_x。我们将此插值x作为输入运行到具有平方 relu 激活的 2 层前馈网络，最后与另一个前馈网络的 sigmoid 激活相乘（在经典 RNN 术语中，这称为门控）。

请注意，就内存使用而言，矩阵Wk,Wr,Wv包含几乎所有参数（1024×1024 matrices它们是矩阵，而其他变量只是 1024 维向量）。矩阵乘法（@在 python 中）贡献了绝大多数所需的计算。

Time mixing 时间混合

def time_mixing(x, last_x, last_num, last_den, decay, bonus, mix_k, mix_v, mix_r, Wk, Wv, Wr, Wout):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    v = Wv @ ( x * mix_v + last_x * (1 - mix_v) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )

    wkv = (last_num + exp(bonus + k) * v) /      \
          (last_den + exp(bonus + k))
    rwkv = sigmoid(r) * wkv

    num = exp(-exp(decay)) * last_num + exp(k) * v
    den = exp(-exp(decay)) * last_den + exp(k)

    return Wout @ rwkv, (x,num,den)
1
2
3
4
5
6
7
8
9
10
11
12
13

时间混合的开始类似于通道混合，通过将此标记的插入x到最后一个标记的x。然后我们应用学到的矩阵以获得“key”, “value” and “receptance”向量。

下一部分是魔法发生的地方。

RWKV 注意力机制

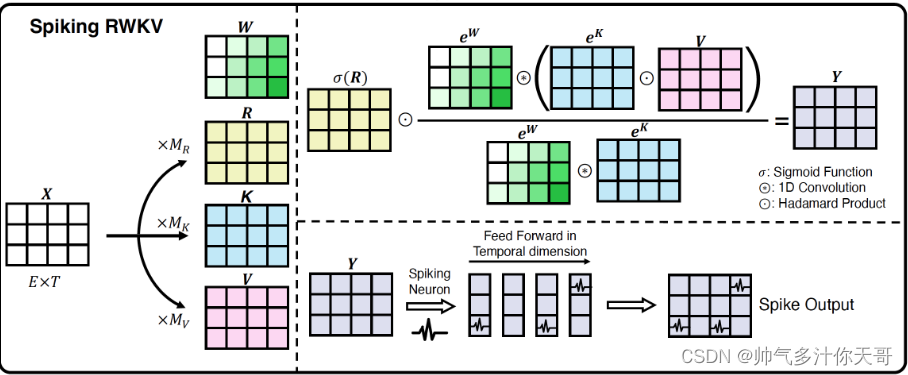
以下为翻译内容 没眼看 还是看生肉原汁原味

在进入该机制的核心之前，我们将观察到虽然进入注意力机制的变量都是 1024 维的（我们说它们有 1024
个通道），但所有通道都是相互独立计算的。因此，我们将只查看单个通道发生的情况，将变量视为标量。

现在，让我们看看变量num。为了使数学符号更清晰，让我们将num和den重命名为α and β . 每一对α and β都存储在
RWKV State。对于每个新Token， α 计算为 αi=e−wαi−1+ekivi，i是Token的index。我们定义w = exp(decay)，请注意w始终为正。通过归纳αi=∑j=1ie−(i−j)w+kjvj… 相似地，.
注意看起来像的加权总和， 尽管只是权重的总和。所以成为加权平均.插入公式和的定义wkv，并表示bonus为,
我们得到所以是加权平均值根据权重,
同时也是当前给出一个bonus(）额外的重量，和以前距离越远，几何权重越小。作为参考，标准Transformer注意力采用“查询”、“键”和“值”向量和输出.计算后wkv，时间混合乘以“接收”
sigmoid®。它在返回结果之前进行最后的线性变换。

转换为输出概率

经过24层时间混合和通道混合后，我们需要将最终输出转换为下一个token的预测概率。

x = layer_norm(x, *params('ln_out'))
x = params('head')[0] @ x

e_x = exp(x-np.max(x))
probs = e_x / e_x.sum() # Softmax of x
1
2
3
4
5

首先，我们进行层归一化。然后，我们乘以一个50277X1024 params('head')[0]由 RWKV 参数给出的矩阵，给我们一个 50277 维的向量。为了获得标记的概率分布（即总和为 1 的 50277 维非负向量）， “softmax”函数 的 softmax x只是exp(x)/sum(exp(x)). 但是计算exp(x)会造成数值溢出，所以我们计算等价函数exp(x-max(x))/sum(exp(x-max(x)))。

就是这样！现在您确切地了解了 RWKV 是如何生成文本的。

实际考虑

实际上，我在简化代码中忽略了一些问题。最重要的是，在实践中，我们非常关心代码的性能/运行时间。这导致我们在 GPU 上并行运行 RWKV，使用用 CUDA 编写的专用 GPU 代码，使用 16 位浮点数等等。

数值问题

一个 16 位浮点数 (float16) 可以表示的最大数字是 65 504，任何超过它的都会溢出，这是不好的。大多数代码对此没有问题，部分原因是层规范化将值保持在合理范围内。然而，RWKV 注意力包含指数级大的数字 ( exp(bonus + k))。在实践中，RWKV 注意力的实现方式是我们从中提取指数因子num并将den所有内容保持在 float16 范围内。例如，请参阅RWKV 中的 time_mixing 函数，共 150 行。

训练

我们只是在示例中加载了预训练模型。为了训练模型，需要计算长文本预测概率的交叉熵损失（我们的示例模型是在pile上训练的）。接下来，计算该损失相对于所有 RWKV 参数的梯度。该梯度用于使用称为 Adam 的梯度下降变体来改进参数。重复很长时间，就得到训练好的RWKV模型。

GPT模式

我的简化代码一个一个地处理Token，这比并行处理它们要慢得多，尤其是在 GPU 上运行时。对于推理，没有办法解决这个问题，因为我们需要先对一个标记进行采样，然后才能使用它来计算下一个标记。但是，对于培训，所有文本都已经可用。这让我们可以跨Token并行化。大多数代码都可以像这样直接并行化，因为时间依赖性很小。例如，所有昂贵的矩阵乘法都独立地作用于每个标记，从而获得良好的性能。

然而，RWKV 注意力本质上是顺序的。幸运的是，它的计算量很少（大约比矩阵乘法少 1024 倍），所以它应该很快。可悲的是，pytorch 没有很好的方法来处理这个顺序任务，所以注意力部分变得很慢（甚至与矩阵乘法相比）。因此，我编写了优化的 CUDA 内核来计算 RWKV 注意力，这是我对 RWKV 项目的主要贡献。

JAX 有 jax.lax.scan 和 jax.lax.associative_scan，这允许纯 JAX 实现比纯 pytorch 执行得更好。但是，我仍然估计与 CUDA 相比， JAX 会导致大约 40% 的训练速度变慢（该估计可能已经过时，因为它是为训练相对较小的 1.5B 模型而做出的）

引用

The RWKV language model: An RNN with the advantages of a transformer
How the RWKV language model works