- 1Vue 3 和 Spring Boot 3 的操作流程和执行步骤详解_springboot3 + vue3
- 2NewSQL分布式数据库发展策略讨论_与newsql相关的综述性论文
- 3计算机网络——TCP/UDP_tcp提供面向字节流的传输服务,为实现流传输服务付出了大量开销
- 424数维杯C题18页保姆级思路+代码+后续参考论文_确定天然气水合物资源分布范围意义
- 5从入门到精通,大厂内部整理Android学习路线
- 6鸿蒙内核源码分析 (内核启动篇) | 从汇编到 main ()
- 7【水声通信】基于matlab OFDM-QPSK水声通信仿真(含误码率检测)【含Matlab源码 3954期】_现代水声通信原理与matlab应用
- 8Android Model引入其他aar包 导致无法打包成aar
- 9哈希表(散列表)——C++数据结构详解_哈希表数据结构代码c++
- 10Idea集成git
数据结构导论大题汇总_02142数据结构导论大题
赞
踩
前言:真题汇总搬家了!!!
自考本科数据结构导论(02142)历年(应用题+算法题)真题汇总【20年4月-22年10月】
一、应用题
1.设A、B、C、D、E五个元素依次进栈(进栈后可立即出栈),问能否得到下列序列:(1)A, B, C, D, E;(2)A,C, E, B, D
答:
(1)能,操作过程为:push(A),pop(A),push(B),pop(B),push©,pop©,push(D),pop(D),push(E),pop(E)
(2)不能,不能的理由:对序列(2)中的E,B,D而言,E最先出栈,此时B和D均在栈中,由于B先于D进栈,所以应有D先出栈
2.有一个整数序列,其输入顺序为20,30,90,一10,45,78,试利用栈将其输出序列改变为30,—10,45,90,78,20,试给出该整数序列进栈和出栈的操作步骤。(用push(x)表示x进栈,pop(x)表示x出栈)
答:

3.字符a、b、c、d依次通过一个栈,按出栈的先后次序组成字符串,至多可以组成多少个不同的字符串?并分别写出它们。
答:
14个。dcba cbad cbda cdba bacd badc bcad bcda bdca abcd abdc acbd acdb adcb。
4.设栈S和队列Q的初始状态均为空,7个元素abcdefg依次进入栈S。若每个元素出栈后立即进入队列Q,且7个元素出队的顺序是bdcfeag。
栈S的容量至少是多少?并画出该栈中元素最多时的一个状态示意图。
答:
栈的容量最少是3。
示意图:

5.设一个链栈的输入序列为A、B、C,试写出所得到的所有可能的输出序列。
答:
共有五种可能的输出序列:
输出ABC,A进,A出,B进,B出,C进,C出;
输出BCA,A进,B进,B出,C进,C出,A出;
输出BAC, A进,B进,B出,A出,C进,C出;
输出CBA,A进,B进,C进,C出,B出,A出;
输出ACB, A进,A出,B进,C进,C出,B出。
6.有一个整数序列,其输入顺序为20,30,90,-10,45,78,试利用栈将其输出序列改变为30,-10,45,90,78,20,写出该整数序列进栈和出栈的操作步骤。(用push(x)表示x进栈,pop(x)表示x出栈)
答:
push(20),push(30),pop(30),push(90),push(-10),pop(-10),push(45),pop(45),pop(90),push(78),pop(78),pop(20)
7.设有编号为1,2,3,4的四辆列车,顺序进入一个栈式结构的站台,若列车2最先开出,则列车出站可能的顺序有几种?并写出这四辆列车所有可能的出站顺序。
答:
若列车2最先开出站,则列车出站可能的顺序有5种。列车可能的出站顺序有:2134,2143,2314,2341,2431。
8.如题图所示,在栈的输入端元素的输入顺序为A,5,8,试写出在栈的输出端可以得到的以数字开头的所有输出序列,并写出进栈、出栈的操作过程(用push(x)表示X进栈,pop(x)表示x出栈)。

答:
共3种。
85A:push(A),push(5),push(8),pop(8),pop(5),pop(A)。
58A:push(A),push(5),pop(5),push(8),pop(8),pop(A)。
5A8:push(A),push(5),pop(5),pop(A),push(8),pop(8)。
9.借助于队列能够将含有 n 个数据元素的栈逆置, 比如栈 S 中的元素为{a, b, c}逆置后变成{c, b, a}。 试简述你的解决方案。
答:
先将栈中元素依次出栈并入队列,然后使该队列元素依次出队列并进入栈。
(栈的修改原则是后进先出;队列的修改原则是先进先出。故栈 S 中的元素为{a, b, c}出栈后为{c,b,a}。接着{c,b,a}入队列,再出队列还为{c,b,a}。再入栈{c,b,a},实现了栈逆置。)
10.已知一个 7 * 6 的稀疏矩阵如题图所示,请写出改稀疏矩阵的三元组表示。

答:
(
(0,0,16),
(0,5,-16),
(1,2,3),
(2,3,-8),
(4,0,91),
(6,2,15)
)
11.给定数据序列{46,25,78,62,12,80},试按元素在序列中的次序将它们依次插入一棵初始为空的二叉排序树,画出插入完成后的二叉排序树。
答:

12.高度为h的满二叉树,如果按层次自上而下,同层从左到右的次序从1开始编号。
该树上有多少个结点?
编号为i的结点的左孩子和右孩子(若存在)的编号分别是多少?
答:
- 2h-1
- 左孩子:2i,右孩子2i + 1
13.为便于表示二叉树的某些基本运算。
则深度为 k 的二叉树的顺序存储结构中的数组的大小为多少?
画出如题 30 图所示的二叉树的顺序存储结构示意图。

并说明对一般形态的二叉树不太适合使用顺序存储结构来表示的原因。
答:
- 2k - 1

- 原因:会造成存储空间的浪费现象。
14.某二叉树结点的中序遍历序列为ABCDEFG、后序遍历序列为BDCAFGE。现要求:
画出该二叉树;
写出该二叉树的先序遍历序列;
该二叉树所对应的森林包括几棵树?
答:
-

-
先序遍历序列:EACBDGF
-
该二叉树所对应的森林包括2棵树。
15.已知一棵二叉树的先序遍历结果为ABDCEF,中序遍历结果为DBAECF,请画出该二叉树并写出这棵二叉树的后序遍历序列。
答:

该二叉树的后序遍历序列为:DBEFCA
16.已知一棵二叉树如题图所示,试求该二叉树的先序遍历序列、中序遍历序列、后序遍历序列和层次遍历序列。

先序遍历序列为:ABDGCHF
中序遍历序列为:DGBAHCF
后序遍历序列为:GDBHFCA
层次遍历序列为:ABCDHFG
17.假设一棵二叉树的中序序列与后序序列分别为:BACDEFGH 和 BCAEDGHF.请画出该二叉树。
答:

18.某二叉树结点的中序遍历序列为ABCDEFG、后序遍历序列为BDCAFGE。现要求:
画出该二叉树;
写出该二叉树的先序遍历序列;
该二叉树所对应的森林包括几棵树?

先序遍历序列:EACBDGF
该二叉树所对应的森林包括2棵树。
19.画出题图所示森林转换后所对应的二叉树

答:

20.将题图所示的二叉树转换为对应的树或森林

答:

21.将题图所示的一棵树转换为二叉树

答:

22.先序遍历、 中序遍历一个森林分别等同于先序、 中序遍历该森林所对应的二叉树。现已知一个森林的先序序列和中序序列分别为 ABCDEFIGJH 和 BDCAIFJGHE, 试画出该森林。
答:

23.分别给出森林的先序序列、中序序列。

答:
先序序列为:ABCDEFGHJI
中序序列为:BCDAFEJHIG
24.分别给出树的先序遍历、后序遍历、层次遍历的结点访问序列。

答:
先序遍历得到结点访问序列为:H, A, B,E, G, F, D, C;
后序遍历得到结点访问序列为:B, G, F, D,E, A, C, H;
层次遍历得到结点访问序列为:H, A, C, B, E, G,F, D。
25.假设用于通讯的电文仅由6个字母A,B,C,D,E,F组成,各个字母在电文中出现的频率分别为:6,3,12,10,7,5,试为这6个字母设计哈夫曼树。(构建新二叉树时,要求新二叉树的左子树根的权值小于等于右子树根的权值。)
答:

26.假设某个电文由5个字母a, b, c,d,e组成,每个字母在电文中出现的次数为7, 9, 5, 6, 12。
试为这5个字母设计哈夫曼树。(构建新二叉树时,要求新二叉树的左子树根的权值小于等于右子树根的权值。)
试为上述哈夫曼树写出对应的哈夫曼编码。
答:

a:00
b:01
c:100
d:101
e:11
27.设有字符集{A,B,C,D,E,F},各字符使用频率对应为{2, 4, 5, 13, 9, 18}。试画出哈夫曼树(要求任一结点的左孩子权值小于右孩子)。
答:

28.设某通信系统中一个待传输的文本有6个不同字符,它们的出现频率分别是0.5,0.8,1.4, 2.2,2.3,2.8,试设计哈夫曼编码。
答:
出现频率为0.5的字符编码为1000
出现频率为0.8的字符编码为1001
出现频率为1.4的字符编码为101
出现频率为2.2的字符编码为00
出现频率为2.3的字符编码为01
出现频率为2.8的字符编码为11

29.假设某个电文由5个字母a, b, c,d,e组成,每个字母在电文中出现的次数为7, 9, 5, 6, 12。
试为这5个字母设计哈夫曼树。(构建新二叉树时,要求新二叉树的左子树根的权值小于等于右子树根的权值。)
试为上述哈夫曼树写出对应的哈夫曼编码。

a:00
b:01
c:100
d:101
e:11
30.写出下图所示的有向图邻接矩阵表示和所有拓扑排序序列

答:

所有拓扑排序序列:
DABEFC;
DAEBFC;
31.写出题31图所示的有向带权图的邻接矩阵。
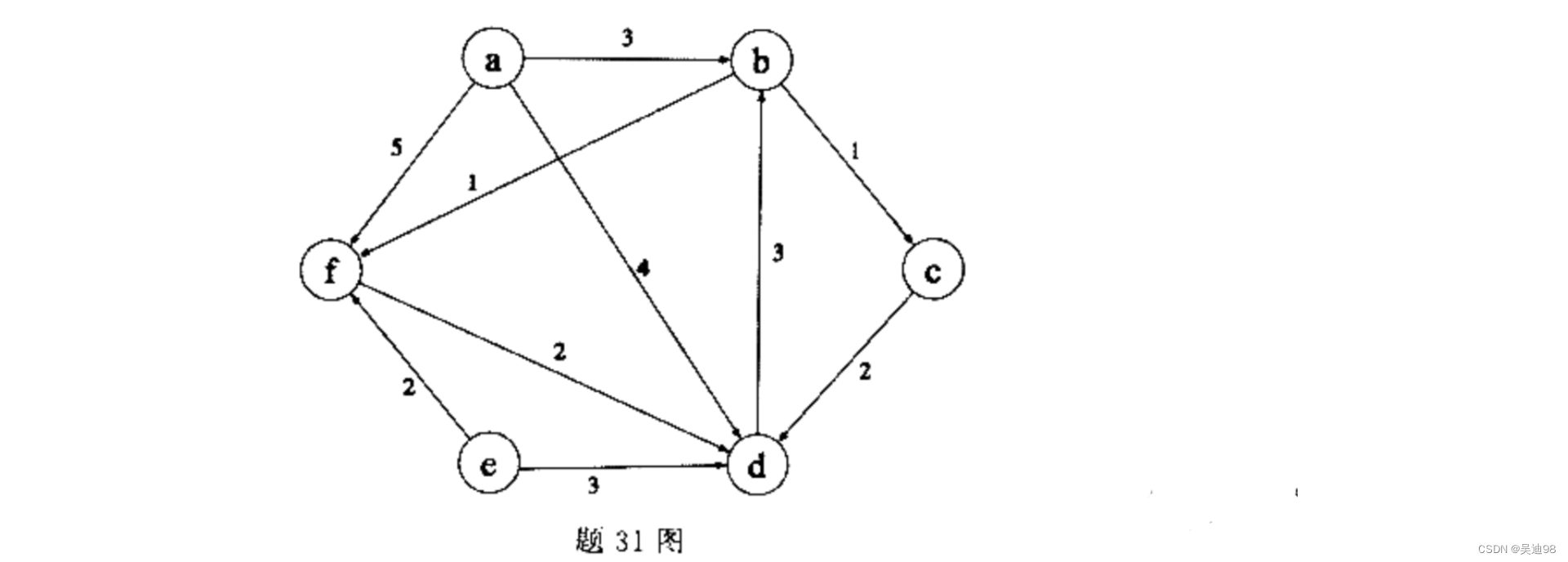
答:

32.假设有一棵完全二叉树按自上而下、从左到右的层序组织包含A、B、C、D、E、F、G这7个结点:
给出其邻接矩阵。
给出其邻接表。
答:
邻接矩阵:

邻接表:

33.题图所示为一有向图,试给出该图的邻接表表示。并给出该图进行拓扑排序的各种可能的拓扑序列。
答:

各种可能的拓扑排序序列为
AEBDC;
AEDBC。
34.设有向图的邻接表表示如题图所示,请给出每个顶点的入度和出度。

答:
V0 的入度:3,出度:0。
V1 的入度:2,出度:2。
V2 的入度:1,出度:2。
V3 的入度:1,出度:2。
V4 的入度:2,出度:3。
V5 的入度:1,出度:1。
35.利用连通分量计算算法求出图中非连通图连通分量的个数。

答:
连通分量1包含以下顶点:V0,V1,V2
连通分量2包含以下顶点:V3,V4
共有2个连通分量。
36.利用Prim算法求图的最小生成树

答:

37.已知如题图所示的无向带权图,请从结点A出发,用普里姆(Prim)算法求其最小生成树,并画出过程示意图。

答:

38.用Kruskal方法求题图所示的图的最小生成树。(要求给出求解过程)

答:

39.求图a所示有向图顶点的拓扑序列,图b是它的邻接表,在表头结点中增加一个数据域in表示相应顶点的入度。

答:
共有五种可能的拓扑序列:
C0->C1->C3->C2->C4
C0->C3->C2->C1->C4
C0->C3->C1->C2->C4
C3->C0->C2->C1->C4
C3->C0->C2->C2->C4
40.题图所示为一有向图,试给出该图的邻接表表示。并给出对该图进行拓扑排序的各种肯能的拓扑序列。

答:

各种可能的拓扑排序序列为
AEBDC;
AEDBC。
41.写出题图所示有向图顶点的所有拓扑排序序列

答:
ABCDEF
ABCEDF
ABDCEF
BACEDF
BACDEF
BADCEF
42.已知散列表的地址空间为0~10,散列函数为H(key)= key mod 11(mod表示求余运算),采用二次探测法解决冲突,试用键值序列20,38,16,27,5,23,56,29建立散列表,并计算出等概率情况下查找成功的平均查找长度。
答:

等概率情况下查找成功的平均查找长度=(1+1+2+3+5+2+3+1)/11=18/11
43.已知题32图所示的二叉排序树中各结点的值分别为1~9,请写出图中结点A~I所对应的值
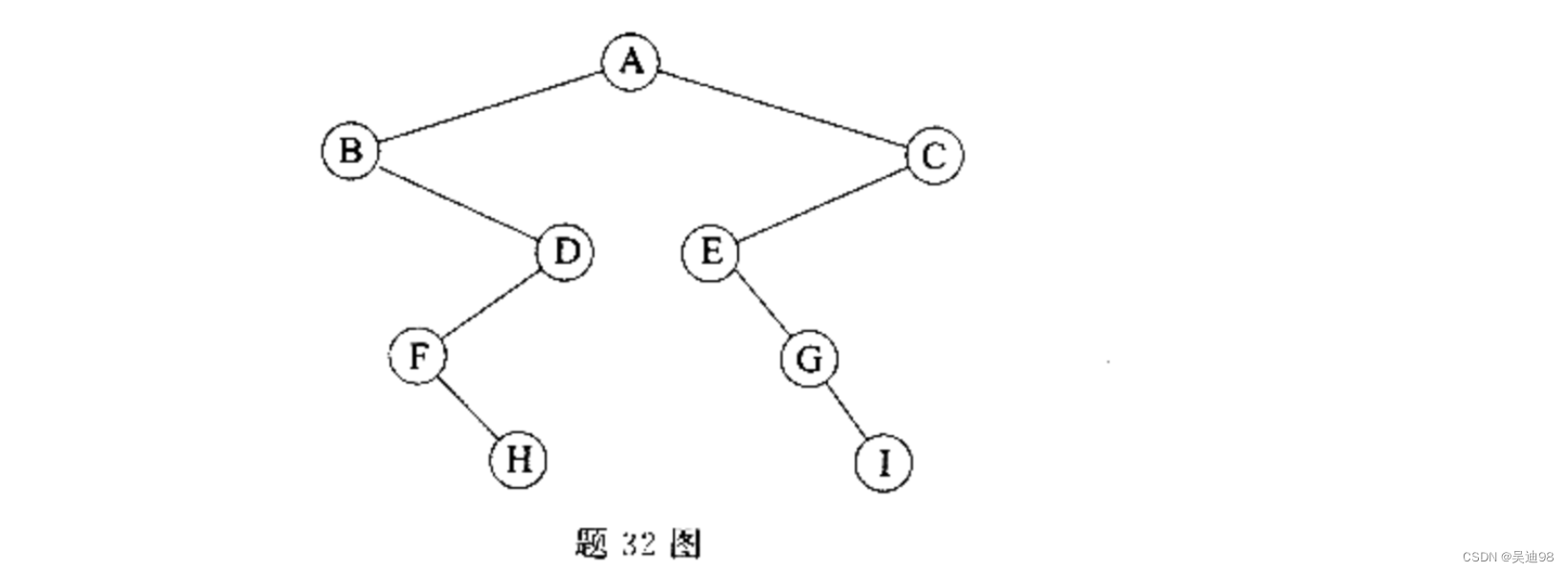
答:
A:5
B:1
C:9
D:4
E:6
F:2
G:7
H:3
I:8
44.要求给出至少2个不同的关键字序列,均能构造出如题图所示的二叉排序树;对此你会得出什么结论?

答:
(1)e,f,g,b,a,d,c或e,b,d,c,a,f,g或e,f,g,b,d,c,a等等。
(2)结论:不同的关键字序列可能会得到相同的二叉排序树。
45.设有一组关键字值序列{e, b, d, f, a, g, c}。 现要求:
根据二叉排序树的创建方法构造出相应的二叉排序树(关键字值的大小按字母表顺序计);
计算等概率情况下在该二叉排序树上查找成功的平均查找长度 ASL。
答:

ASL=(1×1+2×2+3×3+1×4)/7=18/7
46.已知键值序列{11,2,13,26,5,18,4,9},设散列表表长为13,散列函数H(key)=key mod 13,处理冲突的方法为线性探测法,请给出散列表。
答:

47.设散列表长度为11,散列函数H(key)=key mod 11(mod为求余运算),给定的键值序列为:(3,12,13,27,34,22,38,25)。
试画出采用线性探测法解决冲突时所构造的散列表。
依据上述散列表,求出在等概率的情况下査找成功时的平均査找长度。
答:

等概率的情况下査找成功时的平均査找长度=(1+1+1+1+4+1+2+5)/11=16/11
48.已知散列表的长度为11,散列函数H(key)=key%11,采用线性探测法解决冲突。
试用关键字值的序列:75,25,80,35,60,46,50,55,建立散列表。
答:

49.将关键字序列{7,8,30,11,18,9,14}散列存储到一个散列表中,设该散列表的存储空间是一个下标从0开始、大小(HashSize)为10的一维数组,散列函数为H(key)=(key×3)MOD HashSize,处理冲突采用线性探测法。现要求:
(1)画出所构造的散列表。
(2)计算出等概率情况下查找成功的平均查找长度。
答:

等概率的情况下査找成功时的平均査找长度=(1+1+1+1+2+1+1)/ 10=8/10
50.对于给定的一组键值:25.11.22.34.5.44.76.61.100.3.14.120.请分别写出直接插入排序和冒泡排序的第一趟排序结果。
答:
直接插入排序:11,25,22,34,5,44,76,61,100,3,14,120
冒泡排序:11,22,25,5,34,44,61,76,3,14,100,120
51.对键值45 38 66 90 88 10 25 45冒泡排序。
答:

52.试用冒泡法对数列(45, 73, 12, 23, 52, 5, 38)进行递增排序。
写出第1、2、3、4趟排序结果。
给出冒泡排序算法的时间复杂度。
答:

时间复杂度为O(n2)
53.给出一组关键字(20,29,11,74,35,3,8,56),写出冒泡排序前两趟的排序结果,并说明冒泡排序算法的稳定性如何?
答:
第一趟:(20,11,29,35,3,8,56),74
第二趟:(11,20,29,3,8,35),56,74
冒泡排序算法是稳定的排序算法
54.对键值序列(61,87,12,3,8,70)以位于最左位置的键值为基准进行由小到大的快速排序,请写出第一趟排序后的结果,并给出快速排序算法在平均情况和最坏情况下的时间复杂度。
答:
第一趟排序结果:[8 3 12] 61 [87 70]
平均情况下的时间复杂度:O(nlog2n)
最坏情况下的时间复杂度:O(n2)
55.用快速排序方法对关键字序列90 10 25 38 66 88 10进行排序。
答:

56.用快速排序方法对45 38 66 90 88 10 25 45进行排序。
答:

57.采用快速排序方法对关键字序列{265,301,751,129,937,863,742,694,076,438}进行升序排序,写出其每趟排序结束后的关键字序列。
答:
初始态:[265 301 751 129 937 863 742 694 076 438]
第一趟:[076 129] 265 [751 937 863 742 694 301 438]
第二趟:076 [129] 265 [438 301 694 742] 751 [863 937]
第三趟:076 129 265 [301] 438 [694 742] 751 863 [937]
第四趟:076 129 265 438 694 [742] 751 863 937
第五趟:076 129 265 438 694 742 751 863 937
58.设有键值序列如题表所示,现采用快速排序算法以位于最左位置的键值为基准对它进行排序。请给出57,72,88这三个元素在第一趟快速排序后的位置。

答:
元素57在位置2;
元素72在位置5;
元素88在位置8。
59.将一组键值{83,69,41,22,15,33,8,76}应用二路归并排序算法从小到大排序,试写出各趟排序的结果。
答:
初始键值:[83][69][41][22][15][33][8][76]
第一趟:[69 83][22 41][15 33][8 76]
第二趟:[22 41 69 83][8 15 33 76]
第三趟:[8 15 22 33 41 69 76 83]
60.若采用二路归并排序方法对关键字序列{25, 9, 78, 6, 65, 15, 58, 18, 45, 20}进行升序排序, 写出其每趟排序结束后的关键字序列。
答:
初始态: [25] [9][78][6][65][15][58][18][45][20]
第一趟: [9 25] [6 78] [15 65] [18 58] [20 45]
第二趟: [6 9 25 78] [15 18 58 65] [20 45]
第三趟: [6 9 15 18 25 58 65 78] [20 45]
第四趟: [6 9 15 18 20 25 45 58 65 78]
二、算法设计题
1.假定线性表的数据元素的类型为Data Type,顺序表的结构定义如下:
const int Maxsize = 100;
typedef struct {
Data Type data[Maxsize];
int length;
} SeqList;
SeqList L;
- 1
- 2
- 3
- 4
- 5
- 6
设计算法实现顺序表的插入运算InsertSeqlist(SeqList L,Data Type x, int i)。该算法是指在顺序表的第I(1≤i≤n+1)个元素之前,插入一个新元素x。使长度为n的线性表(a1,a2,…ai-1,ai,…,an)变为长度为n+1的线性表(a1,a2,…ai-1,x,ai,…,an)
参考答案:
void InsertSeqList(SeqList L, DataType x, int i) {
// 将元素x插入到顺序表L的第i个数据元素之前
if (L.length == Maxsize) exit("表已满");
if (i < 1 || i > L.length + 1) exit("位置错"); // 检查插入位置是否合法
for (j = L.length; j >= i; j--) { // 初始i=L.length
L.data[j] = L.data[j - 1]; // 依次后移
}
L.data[i - 1] = x; // 元素x置入到下标为i - 1的位置
L.length++; // 表长度加1
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
2.给出图中学生档案信息表的链接存储实现。

参考答案:
typedef struct {
int num; // 学号
char name[8]; // 姓名
char sex[2]; // 性别
int age; // 年龄
int score; // 入学成绩
} DataType; // 定义结点的类型
typedef struct node {
DataType data; // 数据域
struct node * next; // 指针域
} Node, *LinkList; // Node是链表结点的类型
LinkList head;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
3.编写算法,完成按递增次序打印给定的单链表head中各结点的操作,打印的方法是每一次寻找链表中值最小的结点,打印该结点后,把它从链表中删除,重复此操作直到链表为空。
参考答案:
typedef struct node {
DataType data;
struct node *next;
} Node, *LinkList;
print_link_list(LinkList head) {
// q和s是当前比较的俩个结点,p是q的前驱,r是s的前驱
LinkList p, q, r, s;
while (head -> next != NULL) {
p = q = r = head -> next;
s = r -> next;
while (s != NULL) {
if (s -> data < q -> data) {
p = r;
q = s;
}
r = s;
s = r -> next;
}
printf("%d", q -> data);
if (q == head -> next) {
head = q -> next;
} else {
p -> next = q -> next;
}
free(q); // 释放当前值最小的结点空间
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
4.假设单链表的类型定义如下:
typedef struct node {
DataType data;
struct node *next;
} Node, *LinkList;
- 1
- 2
- 3
- 4
设计算法InitiateLinkList()实现单链表的初始化。
参考答案:
LinkList InitiateLinkList() {
LinkList head;
head = malloc(sizeof(Node));
head -> next = NULL;
return head;
}
- 1
- 2
- 3
- 4
- 5
- 6
5.已知带头结点的单链表L是按数据域值非递减有序链接的,试写一算法将值为x的结点插入表L中,使得L仍然是有序链接的。
参考答案:
int Linklist_Insert(Linklist L, DataType x) {
LinkList s;
LinkList p = L -> next; // p是工作指针
LinkList q = L; // q是工作指针
// 从头结点往尾找x在链表中插入位置
while((p != NULL) && (p -> data < x)) {
q = p;
p = p -> next;
}
s = malloc(sizeof(Node));
s -> data = x; // 准备数据值为x结点s
s -> next = p;
q -> next = s; // 将x链路链表中
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
6.设带头结点的单链表的结点结构如下:
typedef struct node {
DataType data;
struct node *next;
} Node, *LinkList;
- 1
- 2
- 3
- 4
试编写一个函数int count(LinkList head, DataType x)统计单链表中数据域为x的结点个数。
参考答案:
int count(LinkList head, DataType x) {
LinkList p = head -> next;
int m = 0;
while (p != NULL) {
if (p -> data == x) m++;
p = p -> next;
}
return m;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
7.假设有两个按元素值递增有序排列的且带头结点的单链表A和表B,请编写算法将表A和表B合并成一个按元素值递减有序排列的单链表C,并要求利用原表(即表A和表B)的结点空间存放表C。
参考答案:
merge_AB_C(LinkList A, LinkList B, LinkList C) {
LkList p, q;
p = A -> next;
q = B -> next;
r = NULL;
while (p != NULL && q != NULL) {
if (p -> data <= q -> data) {
s = p -> next;
p -> next = r;
r = p;
p = s;
} else {
s = q -> next;
q -> next = r;
r = q;
q = s;
}
}
while (p != NULL) {
s = p -> next;
p -> next = r;
r = p;
p = s;
}
while (q != NULL) {
s = q -> next;
q -> next = r;
r = q;
q = s;
}
C = A;
C -> next = r;
free(B);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
8.已知一单链表中的数据元素含有三类字符(即字母字符、数字字符和其他字符)。试编写算法,构造三个单循环链表,使每个循环链表中只含同一类的字符,且利用原表中的结点空间作为这三个表的结点空间(头结点可另辟空间)。
参考答案:
void LinkList_Divide(LinkList L, LinkList A, LinkList B, LinkList C) {
// 把单链表L的元素按类型分为三个循环链表
s = L -> next;
A = malloc(sizeof(Node));
p = A;
B = malloc(sizeof(Node));
q = B;
C = malloc(sizeof(Node));
r = C;
while(s) {
// 单词
if (isalphabet(s -> data)) {
p -> next = s;
p = s;
} else if (isdigit(s -> data)) {
q -> next = s;
q = s;
} else {
r -> next = s;
r = s;
}
s = s -> next;
}
p -> next = A;
q -> next = B;
r -> next = c;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
9.某电商有关手机的库存信息, 按其价格从低到高存储在一个带有头结点的单循环链表中, 链表中的结点由品牌型号(nametype)、 价格(price)、 数量(quantity)和指针(next)四个域组成。 现新到 m 台、 价格为 c、 品牌型号为 x 的新款手机需入库
请写出相应的存储结构以及实现该存储结构的算法。
参考答案:
// 存储结构:
typedef struct node {
char *nametype;
float price;
int quantity;
struct node *next;
} Node, *LinkedList;
// 实现该存储结构的算法:
void InsertData(LinkedList head, char *x, int m, float c) {
head1 = (Node *)malloc(sizeof(Node));
head1 -> nametype = x;
head1 -> price = c;
head1 -> quantity = m;
head1 -> next = NULL;
q = head;
p = head -> next;
while(p != head && p -> price < c) {
q = q -> next;
p = p -> next;
}
head1 -> next = p;
q -> next = head1;
return;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
10.可以在一个数组中保存两个栈:一个栈以数组的第一个单元作为栈底,另一个栈以数组的最后一个单元作为栈底。

设S是其中一个栈,试编写 出栈函数Pop(S)。提示:设其中一个栈标识为0,另一个栈为标识1。
参考答案:
int Pop(Dub_StackTp *S, int i) {
if (S -> top[i] == i * (M - 1)) {
printf("栈空");
return 0;
} else {
S -> top[i] = s -> top[i] - 1 + 2 * i;
return 1;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
11.阅读下列程序片断,写出程序的运行结果。

参考答案:
ABCDEFGHIJK
KJIHGFEDCBA
12.写一个算法,借助栈将图所示的带头结点的单链表逆置。

参考答案:
void ReverseList(LkStk *head) {
LkStk *S;
DataType x;
InitStack(S); // 初始化链栈
p = head -> next;
while (p != NULL) { // 扫描链表
Push(S, p -> data); // 元素进栈
p = p -> next;
}
p = head -> next;
while (!EmptyStack(S)) { // 栈不为空时
p -> data = Gettop(S); // 元素填入单链表中
Pop(S); // 出栈
p = p -> next;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
13.假定循环队列的类型定义如下:
const int maxsize = ...;
typedef struct cycqueue {
DataType data[maxsize];
int front, rear;
} CycqueueTp;
- 1
- 2
- 3
- 4
- 5
参考答案:
计数器初始化为0,从队首开始沿着队列顺序搜索,每走过一个元素,计数器加1,直到队尾,计数器的最终值即队列长度。算法描述如下:
int que_length(CycqueueTp *cq) {
int n, k;
n = 0; // 计数器
k = cq -> front;
while (k != cq -> rear) {
n++;
k = (k + 1) % maxsize;
}
return n;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
14.假设以带头结点的循环链表表示队列,并且只设一个指针指向队列尾结点(注意不设头指针),试编写相应的入队列算法。
typedef struct linked_queue {
DataType data;
struct linked_queue *next;
} LqueueTp;
- 1
- 2
- 3
- 4
参考答案:
void EnQueue(LqueueTp *rear, DataType x) {
LqueueTp *p;
p = (LqueueTp *)malloc(sizeof(LqueueTp));
p -> data = x; // 准备新结点
p -> next = rear -> next;
rear -> next = p; // 新结点链入队列尾
rear = p; // 移动队列尾指针
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
15.假设以带头结点的循环链表表示队列,并且只设一个指针指向队列尾结点(注意不设头指针),试编写相应的初始化队列算法。
typedef struct linked_queue {
DataType data;
struct linked_queue *next;
} LqueueTp;
- 1
- 2
- 3
- 4
参考答案:
void InitQueue(LqueueTp *rear) {
LqueueTp *p;
p = (LqueueTp *)malloc(sizeof(LqueueTp));
rear = p;
// 将队列设置成循环链表,且置队列为空
rear -> next = rear;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
16.假设以数组cycque[m]存放循环队列的元素,同时设变量rear和quelen分别指示循环队列中队列尾元素位置和内含元素的个数。此循环队列的队列满和队列空的条件如下,写出相应的出队列的算法。
typedef struct cycqueue {
DataType data[m];
int rear;
int quelen;
} CycqueueTp;
CycqueueTp *cq;
// 该循环队列的队列满的条件是:(cq -> quelen == m)。
// 该循环队列的队列空的条件是:(cq -> quelen == 0)。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
参考答案:
int OutCycQueue(CycqueueTp *cq) {
if (cq -> quelen == 0) {
printf("队列空");
return 0;
} else {
cq -> quelen = cq -> quelen - 1;
*x = cq -> data[(cq -> rear + m - cq -> quelen) % m];
return 1;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
17.假设以数组cycque[m]存放循环队列的元素,同时设变量rear和quelen分别指示循环队列中队列尾元素位置和内含元素的个数。此循环队列的队列满和队列空的条件如下,写出相应的取队列首元素的算法。
typedef struct cycqueue {
DataType data[m];
int rear;
int quelen;
} CycqueueTp;
CycqueueTp *cq;
// 该循环队列的队列满的条件是:(cq -> quelen == m)。
// 该循环队列的队列空的条件是:(cq -> quelen == 0)。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
参考答案:
DataType GetHead(CycqueueTp *cq) {
DataType x;
x = cq -> data[(cq -> rear + m - cq -> quelen) % m];
return x;
}
- 1
- 2
- 3
- 4
- 5
18.在日常生活中,到银行办理业务时,往往需要排队等候,“在电脑上取号”用命令A表示,“客户到相应的窗口接受服务”用命令N表示,命令Q表示不再接受取号,已排队等候的人依次接受服务。
队列采用链队,DataType 为 int。链队结构用类C语言算法描述如下:
typedef struct LinkQueueNode {
int data;
struct LinkQueueNode *next;
} LkQueNode;
typedef struct LinkQueue {
LkQueNode *front, *rear;
} LkQue;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
用类C语言描述上述等待和接受服务算法。
参考答案:
void GetService() {
LkQue LQ;
int n;
char ch;
int endTag = 0;
InitQueue(&LQ);
while (endTag == 0) {
printf("\n 请输入命令:");
scanf("%c", &ch);
switch(ch) {
case 'A':
printf("客户取号 \n");
scanf("%d", &n);
EnQueue(&LQ, n);
break;
case 'N':
if (!EmptyQueue(LQ)) {
n = Gettop(LQ); // 取队列首结点元素
OutQueue(&LQ); // 出队列
printf("号为 %d 的客户接受服务", n);
} else {
printf("无人等待服务 \n");
}
break;
case 'Q':
printf("排队的人依次接受服务\n");
break
}
if (ch == 'Q') {
while(!EmptyQueue(LQ)) {
n = Gettop(LQ);
OutQueue(&LQ);
printf("号为 %d 的客户接受服务", n);
}
endTag = 1; // 结束所有循环
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
19.读入 n = 100个整数到一个数组中,写出实现将该组数进行逆置的算法,并分析算法的空间复杂度。
参考答案:
void reverseArr(int a[], int n) {
int i, temp;
for (i = 0; i <= n / 2 - 1; i++) {
temp = a[i];
a[i] = a[n - 1 - i];
a[n - 1 - i] = temp;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
reverseArr算法所需要的辅助变量为2个整型变量 i 和 temp,与问题的规模无关,其空间复杂度为 O(1)。
20.写出实现对一个n * n阶矩阵进行转置的算法。
参考答案:
void MM(int A[n][n]) {
int i, j, temp;
for (i = 0; i < n; i++) {
for (j = 0; j < i; j++) {
temp = A[i][j];
A[i][j] = A[j][i];
A[j][i] = temp;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
21.编写算法,将稀疏矩阵转换为三元组的表示形式

三元组的类型定义如下:
#define maxnum 10;
typedef struct node {
int i, j; // 非0元素所在行号,列号
DataType v; // 非0元的值
} Node;
typedef struct spmatrix {
int mu, nu, tu; // 行数、列数、非0元素的个数
Node data[maxnum + 1]; // 这里假定三元组的下标的起始值为1
} SpMatrixTp;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
参考答案:
Matrix_to_Spmatrix(DataType mat[][10], int m, SpMatrixTp *a) {
int i, j;
int n = 10; // 假定稀疏矩阵每行有10个元素
q = 0;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) {
if (mat[i][j] != 0) {
q++;
(*a).data[q].i = i;
(*a).data[q].j = j;
(*a).data[q].v = mat[i][j];
}
}
(*a).mu = m;
(*a).nu = n;
(*a).tu = q;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
22.已知二叉链表的类型定义如下:
typedef struct btnode {
DataType data;
struct btnode *lchild, *rchild;
} *BinTree;
- 1
- 2
- 3
- 4
以二叉链表作存储结构,试编写求二叉树叶子结点个数的算法leafnode_num(BinTree bt).
参考答案:
int leafnode_num(BinTree bt) {
if (bt == NULL) {
return 0;
}
if ((bt -> lchild == NULL) && (bt -> rchild == NULL)) {
return 1;
}
return leafnode_num(bt -> lchild) + leafnode_num(bt -> rchild);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
23.写出复制一棵二叉树的算法。设原二叉树根结点由指针root指向,复制得到的二叉树根结点由指针newroot指向,函数头为:void CopyTree(BTNoderoot,BTNode, newroot),
二叉树的存储结构为:
typedef struct btnode {
DataType data;
struct btnode *lchild, *rchild;
} BTNode, *BTree;
- 1
- 2
- 3
- 4
参考答案:
void CopyTree(BTNode *root, BTNode *newroot) {
if (!root) {
newroot == NULL;
} else {
newroot == (BTNode *)malloc(sizeof(BTNode));
CopyTree(root -> lchild, newroot -> lchild);
CopyTree(root -> rchild, newroot -> rchild);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
24.以二叉链表作存储结构,
试写出二叉链表的结构类型定义。
并编写出二叉树叶子结点个数的算法。
参考答案:
// 二叉链表的结构类型定义
typedef struct btnode {
DataType data;
struct btnode *lchild, *rchild; // 指向左右孩子的指针
} *BinTree;
// 获取二叉树叶子结点个数的算法
int leafnode_num(BinTree bt) {
if (bt == NULL) {
return 0;
}
if ((bt -> lchild == NULL) && (bt -> rchild == NULL)) {
return 1;
}
return leafnode_num(bt -> lchild) + leafnode_num(bt -> rchild);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
25.已知二叉链表的类型定义如下:
typedef struct btnode {
DataType data;
struct btnode *lchild,*rchild;
} *BinTree;
- 1
- 2
- 3
- 4
利用二叉树遍历的递归算法,设计求二叉树的高度的算法Height(BinTree bt)。
参考答案:
int Height(BinTree bt) {
int lh, rh;
if (bt == NULL) return 0;
lh = Height(bt -> lchild);
rh = Height(bt -> rchild);
return 1 + (lh > rh ? lh : rh);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
26.已知二叉链表的类型定义如下:
typedef struct btnode {
DataType data;
struct btnode *lchild,*rchild;
} *BinTree;
- 1
- 2
- 3
- 4
假定 visit(bt)是一个已定义的过程,其功能是访问指针bt所指结点,设计递归算法preorder(BinTree bt)实现在二叉链表上的先序遍历
参考答案:
void preorder(BinTree bt) {
if (bt != NULL) {
visit(bt);
preorder(bt -> lchild);
preorder(bt -> rchild);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
27.给出用类C语言实现非递归先序二叉树的算法
参考答案:
// 非递归先序遍历二叉树
void PreOrder(BinTree t) {
BinTree p;
LkStk *LS; // LS为指向链栈的指针
if (t == NULL) return;
InitStack(LS);
p = t;
// 循环条件是当指针或栈其中一个不为空
while (p != NULL || !EmptyStack(LS)) {
if (p != NULL) {
visit(p -> data); // 访问结点的数据
Push(LS, p); // 将当前指针压入栈中
p = p -> lchild; // 将指针指向p的左孩子
} else {
p = Gettop(LS); // 取栈顶元素
Pop(LS); // 出栈
p = p -> rchild; // 指针指向它的右孩子
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
28.给出无向带权图邻接矩阵的建立算法
参考答案:
void CreateGraph(Graph *g) {
int i, j, n, e, w;
char ch;
scanf("%d %d", &n, &e);
g -> vexnum = n;
g -> arcnum = e;
for (i = 0; i < g -> vexnum; i++) {
scanf("%c", &ch);
g -> vexs[i] = ch;
}
for (i = 0; i < g -> vexnum; i++) {
for (j = 0; j < g -> vexnum; j++) {
g -> arcs[i][j] = MAX_INT;
}
}
for (k = 0; k < g -> arcnum; k++) {
scanf("%d %d %d", &i, &j, &w);
g -> arcs[i][j] = w;
g -> arcs[j][i] = w;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
29.写出向存储结构为邻接矩阵的无向图 G 中插入一条边(x, y)的算法。 算法的头函数为: void AddEdgetoGraph(Graph *G,VertexType x, VertexType y),无向图G的存储结构为:
#define MaxVertex num
typedef char VertexType;
typedef int EdgeType;
typedef struct graph {
int n, e; // 图的实际顶点数和边数
EdgeType edge[MaxVertex][MaxVertex]; // 邻接矩阵
VertexType vertex[MaxVertex]; // 顶点表
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
参考答案:
void AddEdgetoGraph(Graph *G, VertexType x, VertexType y) {
i = -1; j = -1;
// 查找x,y的编号
for (k = 0; k < G -> n; k++) {
if (G -> vertex[k] == x) i = k;
if (G -> vertex[k] == y) j = k;
}
if (i == -1 || j == -1) {
Error("结点不存在");
} else {
G -> edge[i][j] = 1;
G -> edge[j][i] = 1;
G -> e++;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
30.给出建立有向图的邻接表的算法
参考答案:
CreateAdjlist(Graph *g) {
int n, e, i, j, k;
ArcNode *p;
scanf("%d %d", n, e); // 读入顶点数和边数
g -> vexnum = n;
g -> arcnum = e;
for (i = 0; i < n; i++) {
g -> adjlis[i].vertex = i; // 初始化顶点Vi的信息
g -> adjlis[i].firstarc = NULL; // 初始化i的第一个邻接点为NULL
}
for (k = 0; k < e; k++) { // 输入e条弧
scanf("%d %d", &i, &j);
p = (ArcNode *)malloc(sizeof(ArcNode)); // 生成j的表结点
p -> adjvex = j;
p -> nextarc = g -> adjlis[i].firstarc; // 将结点j链到i的单链表中
g -> adjlis[i].firstarc = p;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
31.给出连通图的广度优先搜索算法
参考答案:
void Bfs(Graph g, int v) {
LkQue Q;
InitQueue(&Q); // 初始化队列
visited[v] = 1; // 访问v并置已访问标志
EnQueue(&Q, v); // 访问过的顶点入队列
while (!EmptyQueue(Q)) {
v = Gethead(&Q);
OutQueue(&Q); // 访问过的顶点出队列
// 找g中v的第一个邻接点w
while (w存在) {
if (w未被访问) {
visited[w] = 1; // 访问w并置已访问标志
EnQueue(&Q, w); // 被访问过的顶点入队列
}
w = g 中 v的下一个邻接点;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
32.若图的存储结构为邻接表,队采用链队列,给出相应的广度优先搜索算法。
参考答案:
void Bfs(Graph g, int v) {
LkQue Q; // Q为链队列
ArcNode *p;
InitQueue(&Q);
printf("%d", v);
visited[v] = 1; // 置已访问标志
EnQueue(&Q, v); // 访问过的顶点入队列
while (!EmptyQueue(Q)) {
v = Gethead(&Q);
OutQueue(&Q); // 顶点出队列
p = g.adjlist[v].firstarc; // 找到v的第一个邻接点
while (p != NULL) { // 判断邻接点是否存在
if (!visited[p -> adjvex]) { // 邻接点存在未被访问
printf("%d", p -> adjvex);
visited[p -> adjvex] = 1; // 置已访问标志
EnQueue(&Q, p -> adjvex); // 邻接点入队列
}
p = p -> nextarc; // 沿着v的邻接点链表顺序搜索
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
33.采用邻接矩阵作为存储结构,查找邻接点操作实际上通过循环语句顺序访问邻接矩阵的某一行。给出相应的广度优先搜索算法。
参考答案:
void Bfs(Graph g, int v) {
LkQue Q; // Q为链队列
int j;
InitQueue(&Q);
printf("%d", v);
visited[v] = 1; // 置已访问标志
EnQueue(&Q, v); // 访问过的顶点入队列
while (!EmptyQueue(Q)) {
v = Gethead(&Q);
OutQueue(&Q); // 顶点出队列
for (j = 0; j < n; j++) {
m = g -> arcs[v][j];
// 判断是否邻接点,且未被访问
if (m && !visited[j]) {
printf("%d", j);
visited[j] = 1; // 置已访问标志
EnQueue(&Q, j); // 邻接点入队列
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
34.给出以邻接表为存储结构,通过调用深度优先搜索算法实现的计算连通分量的算法。
参考答案:
int visited[vnum];
Count_Component(Graph g) {
int count, v;
for (v = 0; v < g.vexnum; v++) {
visited[v] = 0;
}
count = 0;
for (v = 0; v < g.vexnum; v++) {
if (!visited[v]) {
count++;
printf("连通分量%d包含以下顶点:", count);
Dfs(g, v);
printf("\n");
}
}
printf("共有%d个连通分量\n", count);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
35.给出拓扑排序算法
参考答案:
Tp_sort(Graph g) {
// 建立图g中入度为0的顶点的栈s;
m = 0; // m记录输出的顶点个数
while (!EmptyStack(S)) { // 当栈非空
Pop(S, v); // 弹出栈顶元素赋值给v
m++;
w = Firstvex(g, v); // 图g中顶点v的第一个邻接点
while (w存在) {
// w的入度-1
if (w的入度 == 0) {
push(s, w);
}
Nextvex(g, v, w); // 图G中顶点v的下一个邻接点
}
}
if (m < n) printf("图中有环\n");
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
36.设计一个算法实现以下功能:在整型数组A[n]中查找值为k的元素,若找到,则输出其位置i(0≤i≤n一1),否则输出一1作为标志。
参考答案:
int search(int A[], int n, int k) {
int i = 0;
int resIndex = -1; // 最终找到的下标位置
while(i <= n - 1) {
if (A[i] != k) {
i++;
} else {
resIndex = i;
break; // 找到了,退出循环
}
}
return resIndex;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
37.假定有序表是按键值从小到大有序,给出二分查找算法。
参考答案:
int SearchBin(SqTable T, KeyType key) {
// 在有序表T中,用二分查找法查找键值等于key的元素
// 变量low和high分别标记查找区间的下界和上界
int low, high;
low = 1;
high = T.n;
// 区间长度不为0时一直找
while (low <= high) {
mid = (low + high) / 2;
if (key == T.elem[mid].key) {
return mid;
} else if (key < T.elem[mid].key) {
high = mid - 1; // 在前半区查找
} else {
low = mid + 1; // 在后半区查找
}
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
38.试写出二分查找的递归算法
参考答案:
int binsearch_2(Sqtable R, KeyType k, int low, int high) {
int mid = (low + high) / 2;
if (R.elem[mid].key == k) {
return mid;
} else if (R.elem[mid].key > k) {
return binsearch_2(R, k, low, mid - 1);
} else {
return binsearch_2(R, k, mid + 1, high);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
39.散列表数据元素的类型定义如下:
const int MaxSize = 20; // 定义散列表的容量
typedef struct {
KeyType key; // 键值域
... // 其他域
} Element;
typedef Element OpenHash[MaxSize];
- 1
- 2
- 3
- 4
- 5
- 6
给出用线性探测法解决冲突的散列表查找运算的实现算法
参考答案:
// 在散列表HL中查找键值为key的结点
// 成功时返回该位置。不成功时返回0
int SearchOpenHash(KeyType key, OpenHash HL) {
d = H(key); // 计算散列地址
i = d;
while ((HL[i].key != NULL) && (HL[i].key != key)) {
i = (i + 1) % m;
}
if (HL[i].key == key) return i;
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
40.给出直接插入排序的算法。
参考答案:
void StraightInsertSort(List R, int n) {
int i, j;
// n为表长,从第二个记录开始进行插入
for (i = 2; i <= n; i++) {
R[0] = R[i]; // 第i个记录复制为岗哨
j = i - 1;
// 与岗哨比较,直至键值不大于岗哨键值
while (R[0].key < R[j].key) {
R[j + 1] = R[j]; // 将第j个记录赋值给第j + 1个记录
j--;
}
R[j + 1] = R[0]; // 将第i个记录插入到序列中
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
41.给出直接选择排序算法。
参考答案:
void SelectSort(List R, int n) {
int min, i, j;
// 每次循环选出一个最小键值
for (i = 1; i <= n - 1; i++) {
min = i; // 假设第i个记录键值最小
for (j = i + 1; j <= n; j++) {
// 记录下键值较小记录的下标
if (R[j].key < R[min].key) {
min = j;
}
}
if (min != i) {
// 将最小键值记录和第i个记录交换
int temp = R[i];
R[i] = R[min];
R[min] = temp;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
42.给出有序序列的合并算法。
参考答案:
void Merge(List a, List R, int h, int m, int n) {
// k,j置成起始位置
k = h;
j = m + 1;
// 将a中记录从小到大合并入R
while ((k <= m) && (j <= n)) {
// a[h]键值小,送入R[k]并修改h值
if (a[h].key <= a[j].key) {
R[k] = a[h];
h++;
} else { // a[j]键值小,送入R[k]并修改j值
R[k] = a[j];
j++;
}
k++;
}
// j > n,将ah,...am剩余部分插入R的末尾
while (h <= m) {
R[k] = a[h];
h++;
k++;
}
// h > m,将am+1,...an剩余部分插入R的末尾
while (j <= n) {
R[k] = a[j];
j++;
k++;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29


