【PAT】2021年秋季PAT甲级题解_pat甲级题目

---

1. Arrays and Linked Lists (20 分)

Let’s design a data structure $A$ that combines arrays and linked lists as the following:

At the very beginning, an integer array $A_0$​ of length $L_0$​ is initialized for the user. When the user tries to access the $i$th element $A[i],\text{if}0\le i<L_0$, then $A[i]$ is just $A_0[i]$. Now our system is supposed to return $h_0+i\times sizeof(int)$ as the accessed address, where $h_0$​ is the initial address of $A_0$​, and $sizeof(int)$ is the size of the array element, which is simply int, taking 4 bytes.

In case there is an overflow of the user’s access (that is, $i\ge L_0$​), our system will declare another array $A_1$​ of length $L_1$​. Now $A[i]$ corresponds to $A_1[j]$ (It’s your job to figure out the relationship between $i$ and $j$). If $0\le j<L_1$​, then $h_1+j\times sizeof(int)$ is returned as the accessed address, where $h_1$​ is the initial address of $A_1$​.

And if there is yet another overflow of the user’s access to $A_1[j]$, our system will declare another array $A_2$​ of length $L_2$​, and so on so forth.

Your job is to implement this data structure and to return the address of any access.

Input Specification:

Each input file contains one test case. For each case, the first line gives 2 positive integers $N(\le 10^4)$ and $K(\le 10^3)$ which are the number of arrays that can be used, and the number of user queries, respectively.

Then $N$ lines follow, each gives 2 positive integers, which are the initial address $(\le 10^7)$ and the length $(\le 100)$ of an array, respectively. The numbers are separated by spaces. It is guaranteed that there is no overlap of the spaces occupied by these arrays.

Finally, $K$ indices of the elements queried by users are given in the last line. Each index is an integer in the range $[0,2^{20}]$.

Output Specification:

For each query, print in a line the accessed address. If the queried index exceeds the range of all the $N$ arrays, output Illegal Access instead, and this query must NOT be processed.

Print in the last line the total number of arrays that have been declared for the whole process.

Sample Input:

6 7
2048 5
128 6
4016 10
1024 7
3072 12
9332 10
2 12 25 50 28 8 39
1
2
3
4
5
6
7
8

Sample Output:

2056
4020
1040
Illegal Access
3072
140
3116
5
1
2
3
4
5
6
7
8

###Hint:

$A[2]$ is just $A_0[2]$, so the accessed address is $2048+2\times 4=2056$.

In order to access $A[12]$, declaring $A_1$​ is not enough, we need $A_2$​ with initial address $h_2=4016$. Since $A[12]=A_2[1]$, the accessed address is $4016+1\times 4=4020$.

In order to access $A[25]$, we need $A_3$​ with initial address $h_3=1024$. Since $A[25]=A_3[4]$, the accessed address is $1024+4\times 4=1040$.

The access of $A[50]$ exceeds the maximum boundary of all the arrays, and hence an illegal access. There is no extra array declared.

In order to access $A[28]$, we need $A_4$​ with initial address $h_4=3072$. Since $A[28]=A_4[0]$, the accessed address is just $3072$.

It is clear to see that $A[8]=A_1[3]$ and hence the accessed address is $128+3\times 4=140$; and $A[39]=A_4[11]$ so the accessed address is $3072+11\times 4=3116$.

All together there are 5 arrays used for the above queries.

题意

本题让我们设计一个数据结构 $A$ ，它结合了数组和链表。一开始就为用户初始化了长度为 $L_0$​ 的整数数组 $A_0$​ 。当用户试图访问这个数据结构 $A$ 的第 $i$ 个元素 $A[i]$ 时，如果 $0\le i<L_0$, 那么 $A[i]$ 就是 $A_0[i]$（即 $A[i]$ 存放在 $A_0[i]$ 位置），系统返回 $h_0+i\times sizeof(int)=h_0+4i$ 作为访问地址，其中 $h_0$​ 是 $A_0$ 的初始地址 。

如果用户的访问超出了 $A_0$ 的范围（即 $i\ge L_0$​)，系统将声明另一个长度为 $L_1$ 的数组 $A_1$​ ，如果 $A[i]$ 对应 $A_1[j]$（$0\le j<L_1$），就返回 $h_1+4j$ 作为访问地址。如果访问再次超出范围，系统将声明另一个长度为 $L_2$ 的数组 $A_2$​ ……依次类推。

其实就是让我们实现一个「数组的链表」，假设其为 $A$ ，这一链表的每个结点都将是一个长度已知的数组，我们可以从第一个数组的第一个位置，依次存放元素。一开始，这一链表中已有第一个结点被开辟出来（一个点），即有第一个数组可用。

现在用户想要存取 $A$ 中第 $i$ 个元素，如果超过了已知的整个链表的范围，我们不做任何处理（一个点）。否则，我们进行如下处理——由于是“链表”，我们不确定「外部的第 $i$ 个元素」到底对应「内部第几个数组的第几个位置」，只能从头开始扫描，如果当前数组（和前面的数组加起来）的空间足以容纳 $i$ 个元素，则第 $i$ 个元素就在当前的数组中；否则开辟下一个结点（即声明下一个数组）（一个点），判断下个数组是否能容纳，依次类推。

最后，要对每个存取打印访问的地址。如果访问的索引超出所有数组的范围，则改为输出 Illegal Access 。在最后一行中，还要打印整个过程之后，已经声明的数组总数。

解法 模拟+数组

这一题其实很简单，别看说的复杂，只要把上面的几个坑点看懂，就没有什么难度。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 10;
int n, k, ac, maxLen = 0;
int declaredCnt = 1; // 声明的数组的个数,一开始就有了A0
struct node { 
	int hi, Li;
	bool declared = false;
} arrays[maxn];

int main() {
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d", &arrays[i].hi, &arrays[i].Li);
		maxLen += arrays[i].Li;
	}
    arrays[0].declared = true;
	while (k--) {
		scanf("%d", &ac);
		if (ac >= maxLen) {
			printf("Illegal Access\n"); // 上溢出所有的数组
			continue;
		}
		for (int i = 0; i < n; ++i) { // 遍历n个数组
			if (arrays[i].declared == false) {
				arrays[i].declared = true;
				++declaredCnt; // 声明的数组+1
			}
			if (ac < arrays[i].Li) { // 当前数组可容纳这次访问
				printf("%d\n", arrays[i].hi + ac * 4);
				break;
			} else ac -= arrays[i].Li;
		}
	}
	printf("%d\n", declaredCnt);
	return 0;	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

---

2. Stack of Hats (25 分)

PATers believe that wearing hats makes them look handsome, so wherever they go, everyone of them would wear a hat. One day they came to a restaurant, a waiter collected their hats and piled them up. But then when they were ready to leave, they had to face a stack of hats as shown by the above figure. So your job is to help them line up so that everyone can pick up his/her hat one by one in order without any trouble.

It is known that every hat has a unique size, which is related to the weight of its owner – that is, the heavier one wears larger hat.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive number $N(\le 10^4)$ which is the number of PATers. The next line gives $N$ distinct sizes of the hats, which are positive numbers no more than $10^5$. The sizes correspond to the hats from bottom up on the stack. Finally in the last line, $N$ distinct weights are given, correspond to the hat owners numbered from $1$ to $N$. The weights are positive numbers no more than $10^6$. All the numbers in a line are separated by spaces.

Output Specification:

For each test case, print in a line the indices of the hat owners in the order of picking up their hats. All the numbers must be separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
12 19 13 11 15 18 17 14 16 20
67 90 180 98 87 105 76 88 150 124
1
2
3

Sample Output:

3 4 8 6 10 2 1 5 9 7
1

Hint:

The 1st hat has the largest size 20, hence must correspond to the one with the largest weight, which is the 3rd one of weight 180. So No.3 must go first.

The 2nd hat has the 6th smallest size 16, hence corresponds to the 6th smallest weight, which is 98. So No.4 is the next to go.

And so on so forth.

题意

PATer们相信戴帽子会让他们看起来很帅，所以无论他们走到哪里，每个人都会戴着帽子。每顶帽子都有一个独特的尺寸，帽子的主人越重，戴的帽子越大。

一天，他们来到一家餐馆，一个服务员把他们的帽子收起来并堆了起来。但是，当他们准备离开时，他们不得不面对一堆帽子，如上图所示。你的工作是帮助他们排队，以使每个人都能一个接一个地、有序拿走自己的帽子。即，从帽子堆顶到堆底，依次让当前帽子的主人拿走帽子。

解法 排序

这道题是四道题中最简单的。关键在于，理解如何有序拿走所有帽子。我们声明两个结构体数组，分别存储PATer们的体重及对应的下标、帽子堆中每顶帽子的尺寸和下标。然后从大到小（体重或尺寸）分别排序两个数组，再从前往后遍历，令对应体重的PATer拿走对应大小的帽子，构造出答案数组——即求出帽子堆中，每个帽子应该被哪个下标编号的PATer拿走。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 10;
int n, ans[maxn];
struct tidx{ int v, idx; } weights[maxn], hats[maxn];
bool cmp(const tidx &a, const tidx &b) {
	return a.v > b.v;	
}
int main() {
	scanf("%d", &n);
	for (int i = 0; i < n; ++i) {
		scanf("%d", &hats[i].v);
		hats[i].idx = i;
	}
	for (int i = 0; i < n; ++i) {
		scanf("%d", &weights[i].v);
		weights[i].idx = i;
	}
	sort(hats, hats + n, cmp);
	sort(weights, weights + n, cmp);
	for (int i = 0; i < n; ++i)
		ans[hats[i].idx] = weights[i].idx + 1;	
	for (int i = 0; i < n; ++i)
		printf(" %d" + !i, ans[n - i - 1]);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

---

3. Playground Exploration (25 分)

A playground is equipped with ball pits and tents connected by tunnels. Kids can crawl through the tunnels to meet their friends at a spot with a tent or a ball pit.

Now let’s mark each meeting spot (a tent or a ball pit) by a number. Assume that once a kid starts to explore the playground from any meeting spot, he/she will always choose the next destination with the smallest number, and he/she would never want to visit the same spot twice. Your job is to help the kids to find the best starting spot so they can explore as many spots as they can.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers $N(\le 100)$, the total number of spots, and $M$, the number of tunnels. Then $M$ lines follow, each describes a tunnel by giving the indices of the spots (from $1$ to $N$) at the two ends.

Output Specification:

Print in a line the best starting spot which leads to the maximum number of spots, and the number of spots a kid can explore. If the solution is not unique, output the one with the smallest index. There must be exactly 1 space between the two numbers, and there must be no extra space at the beginning or the end of the line.

Sample Input:

8 10
1 2
3 4
5 8
1 4
6 1
3 7
2 4
5 3
2 8
2 5
1
2
3
4
5
6
7
8
9
10
11

Sample Output:

6 7
1

Hint:

Actually there are two solutions. Kids can either start from 6 and go through 1->2->4->3->5->8, or from 7 to 3->4->1->2->5->8, both can visit 7 spots. Since 6 is a smaller index, we output 6 as the starting spot.

题意

操场上设有 ball pits 和通过隧道连接的帐篷。孩子们可以爬过隧道，在有帐篷或 ball pit 的地方与朋友见面。

用数字编号每个会面地点（帐篷或 ball pit ）。假设一个孩子从任何一个会面地点出发探索游乐场，他/她总是会选择编号最小的下一个目的地（关键点），他/她永远不会想去同一个地点两次（一个点）。你的工作是帮助孩子们找到最好的出发点，这样他们就可以探索尽可能多的地方（一个点）。

最后，在一行中打印出最佳起始点，从该点出发能探索最大数量的点，以及孩子可以探索的点的数量。如果解决方案不是唯一的，则输出索引最小的解决方案。

解法 图+DFS+贪心

做对这题的关键点在于，看到「总是会选择编号最小的下一个目的地」这一“贪心策略”，剩下的就不难了。使用邻接表建图，注意建图之后，要对每个点的邻接点序列从小到大排序。然后依次以每个点为起始点、用DFS求出可访问的地点数量，取最大可访问的地点数量和下标最小的出发点。也要注意，DFS中使用布尔数组 vis 避免重复访问一个结点。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
int n, m, a, b;
int ans = 1, maxSpots = 1;
vector<int> g[maxn];
bool vis[maxn];
int dfs(int u) {
	vis[u] = true;
	int tmpSpots = 0;
	for (int v : g[u]) {
		if (vis[v] == false) {
			tmpSpots = dfs(v); // 只探索未访问过的、编号最小的结点
			break;
		}
	}
	vis[u] = false;
	return 1 + tmpSpots;
}
int main() {
	cin >> n >> m;
	while (m--) {
		cin >> a >> b;
		g[a].push_back(b);
		g[b].push_back(a);
	}
	for (int i = 1; i <= n; ++i) sort(g[i].begin(), g[i].end());
	for (int i = 1; i <= n; ++i) {
		int spots = dfs(i);
		if (spots > maxSpots) {
			maxSpots = spots;
			ans = i;
		}
	}
	cout << ans << " " << maxSpots;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

---

4. Sorted Cartesian Tree (30 分)

A Sorted Cartesian tree is a tree of (key, priority) pairs. The tree is heap-ordered according to the priority values, and an inorder traversal gives the keys in sorted order. For example, given the pairs { (55, 8), (58, 15), (62, 3), (73, 4), (85, 1), (88, 5), (90, 12), (95, 10), (96, 18), (98, 6) }, the increasing min-heap Cartesian tree is shown by the figure.

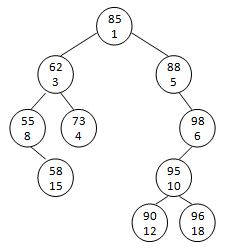
Your job is to do level-order traversals on an increasing min-heap Cartesian tree.

Input Specification:

Each input file contains one test case. Each case starts from giving a positive integer $N(\le 30)$, and then $N$ lines follow, each gives a pair in the format key priority. All the numbers are in the range of int.

Output Specification:

For each test case, print in the first line the level-order traversal key sequence and then in the next line the level-order traversal priority sequence of the min-heap Cartesian tree.

All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
88 5
58 15
95 10
62 3
55 8
98 6
85 1
90 12
96 18
73 4
1
2
3
4
5
6
7
8
9
10
11

Sample Output:

85 62 88 55 73 98 58 95 90 96
1 3 5 8 4 6 15 10 12 18
1
2

题意

一个有序笛卡尔树是一棵元素为 (key, priority) 对的树。这棵树满足在 priority 上是堆序的和中序遍历会得到有序序列这两个性质。现在给出一个 (key, priority) 序列，要求建立一棵有序笛卡尔树，并输出对其进行层序遍历后得到的 key 序列和 priority 序列。

解法 笛卡尔树+递归+左旋/右旋

本题考查的是一种叫做笛卡尔树 Cartesian tree 的数据结构，有兴趣且有时间可以仔细了解一下。不过普通的笛卡尔树效果不是很好，特别是从有序序列生成时，笛卡尔树就退化成了一条链。不过，通过使用优先级特别是随机生成的优先级，我们就得到了大名鼎鼎的Treap。

不难发现，本题的笛卡尔树是一棵二叉搜索树（在 key 上），也是一个最小堆（在 priority 上）。因此，我们只需要按照二叉搜索树的插入方法，依次递归插入每个 (key, priority) 结点；然后在递归返回时，检查优先级是否符合最小堆性质，如果不符合，则使用左旋或者右旋，在保持二叉搜索树的有序性质的同时，将优先级更小的结点旋转上去、优先级更大的结点旋转下来，以保持堆序性……其实就相当于堆的上滤操作。最后，一个层序遍历即可得到答案。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 33;
int n, k, p;
struct node {
	int k, p;
	node *left, *right;
	node() : left(nullptr), right(nullptr) {}
	node(int _k, int _p) : k(_k), p(_p), left(nullptr), right(nullptr) {}
} *root = nullptr;
void L(node* &root) {
	node *newroot = root->right;
	node *tmp = newroot->left;
	root->right = tmp;
	newroot->left = root;
	root = newroot;
}
void R(node* &root) {
	node *newroot = root->left;
	node *tmp = newroot->right;
	root->left = tmp;
	newroot->right = root;
	root = newroot;
}
void insert(node* &root, int k, int p) {
	if (root == nullptr) {
		root = new node(k, p);
		return;
	}
	if (k < root->k) {
		insert(root->left, k, p);
		if (p < root->p) R(root); // 最小堆; 右旋相当于上滤
	} else {
		insert(root->right, k, p);
		if (p < root->p) L(root); // 最小堆; 左旋相当于上滤
	}
}
vector<int> ks, ps;
void level(node *root) {
	queue<node*> q;
	q.push(root);
	while (!q.empty()) {
		node *t = q.front(); q.pop();
		ks.push_back(t->k);
		ps.push_back(t->p);
		if (t->left) q.push(t->left);
		if (t->right) q.push(t->right);		
	}
}
int main() {
	cin >> n;
	for (int i = 0; i < n; ++i) {
		cin >> k >> p;
		insert(root, k, p);
	}
	level(root);
	for (int i = 0; i < n; ++i) printf(" %d" + !i, ks[i]);
	printf("\n");
	for (int i = 0; i < n; ++i) printf(" %d" + !i, ps[i]);
	return 0;	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61