【动态规划专栏】-- 回文串问题 -- 动态规划经典题型

目录

动态规划

动态规划思维（基础）

状态表示（最重要）

状态转移方程（最难）

初始化（细节）

填表顺序（细节）

返回值（结果）

回文子串 ⭐⭐

【题目解析】 

【算法原理】

C++ 算法代码 

最长回文子串 ⭐⭐ 

【题目解析】 

【算法原理】

C++ 算法代码  

回文串分割Ⅳ⭐⭐⭐ 

【题目解析】 

【算法原理】

C++ 算法代码

---

动态规划

动态规划思维（基础）

        动态规划一般会先定义一个dp表，dp表一般为一维数组 / 二位数组。如：一维数组，会先创建一个一维数组（dp表），接下来就是想办法将这个dp填满，而填满之后里面的某一个值就是最终结果。

状态表示（最重要）

#问：是什么？

• 就是dp[i]所代表的含义。

#问：怎么来？

• 题目要求。
• 经验 + 题目要求。
• 分析问题的过程中，发现重复子问题。

状态转移方程（最难）

#问：是什么？

• dp[i] = ?。

初始化（细节）

#问：有什么作用？

• 保证填表的时候不越界。

        dp表是根据状态转移方程进行的，而状态转移方程是通过已有状态推出未知状态。

填表顺序（细节）

#问：有什么作用？

• 为了填写当前状态的时候，所需要的状态已经计算过了。

返回值（结果）

        题目要求 + 状态表示。

⭐⭐⭐DP解回文串问题核心：能够将所有的字串是否是回文的信息，保存在dp表中。

---

回文子串 ⭐⭐

 647. 回文子串 - 力扣（LeetCode）

---

【题目解析】 

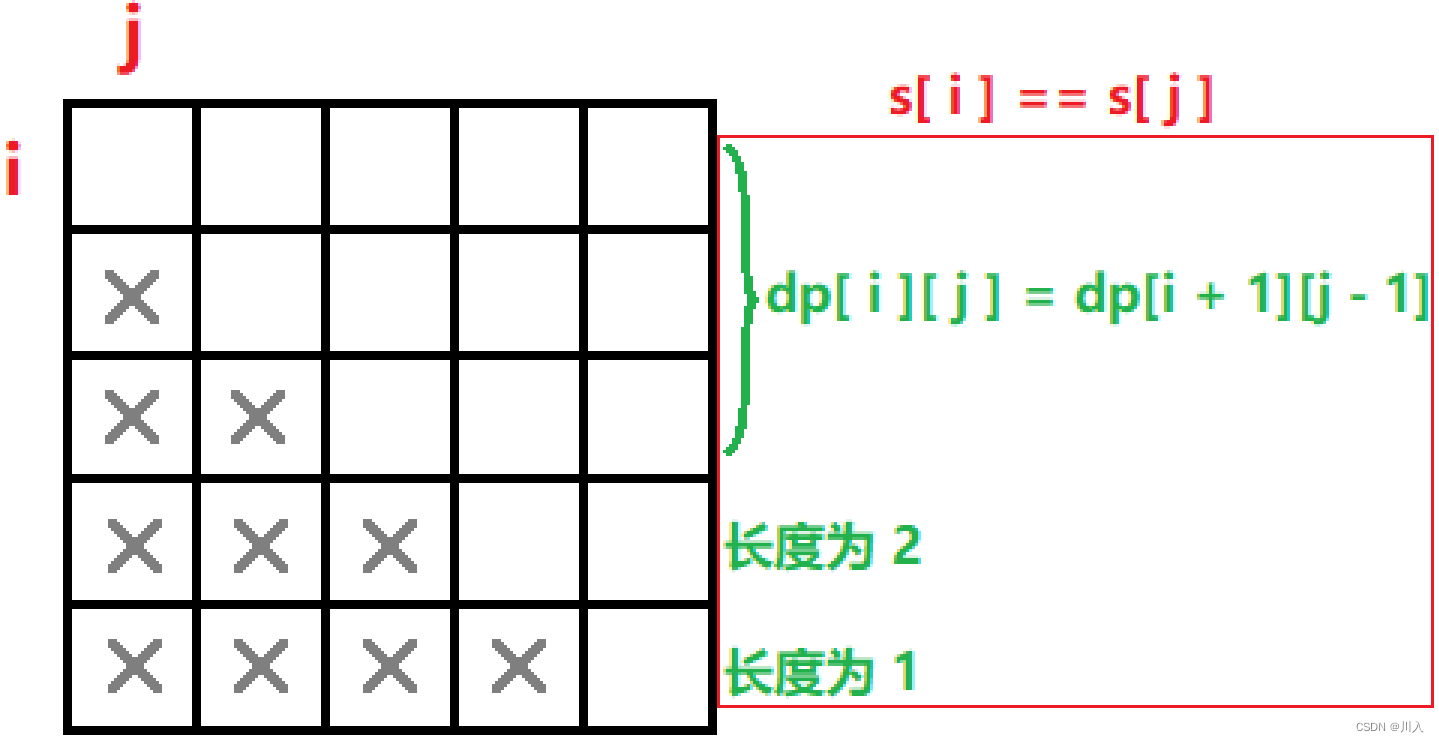
        为了能表示出来所有的子串，我们可以创建⼀个 n * n 的⼆维 dp 表，只用到「上三角部分」即可。 其中， dp[i][j] 表示： s 字符串 [i, j] 的子串，是否是回文串。

        每层逻辑。

【算法原理】

#：状态表示：

#：状态转移方程：

• 当 s[ i ] != s[ j ] 的时候：不可能是回文串， dp[ i ][ j ] = false
• 当 s[ i ] == s[ j ] 的时候：根据长度分三种情况讨论：
  • 长度为 1 ，也就是 i == j ：此时一定是回文串， dp[ i ][ j ] = true
  • 长度为 2 ，也就是 i + 1 == j ：此时也一定是回文串， dp[ i ][ j ] = true
  • 长度大于 2 ，此时要去看看 [ i + 1, j - 1 ] 区间的子串是否回文： dp[ i ][ j ] = dp[i + 1][j - 1] 

#：初始化：

         因为我们的状态转移方程分析的很细致，因此无需初始化。

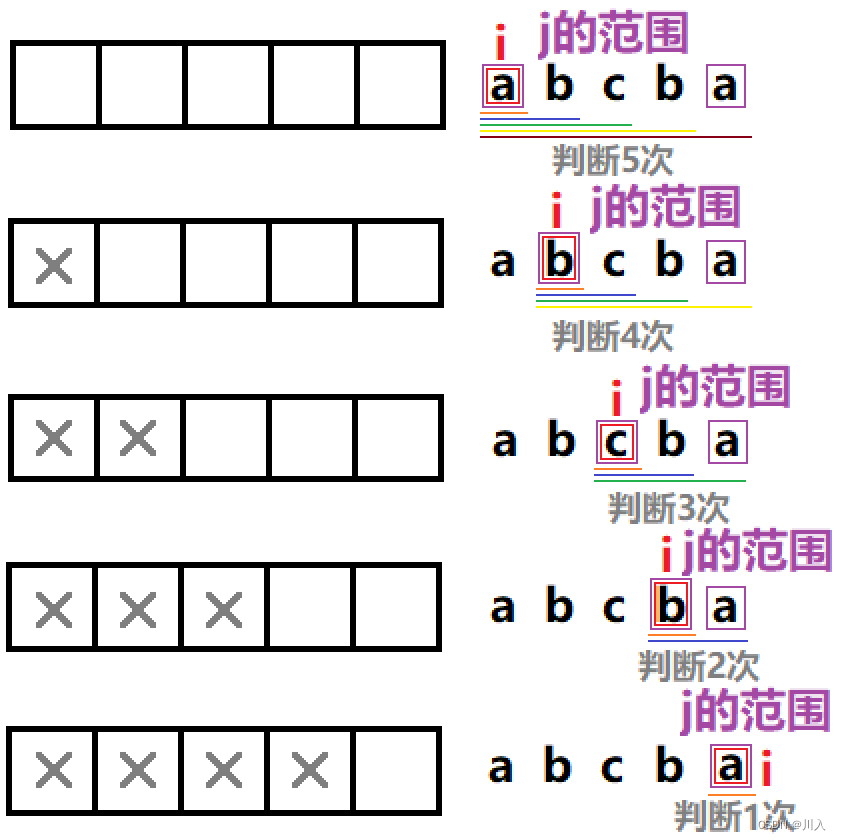
#：填表顺序：

        根据「状态转移方程」，我们需要「从下往上」填写每⼀行，每⼀行的顺序无所谓。

#：返回值：

        根据「状态表示和题目要求」，我们需要返回 dp 表中 true 的个数。 

---

C++ 算法代码 

class Solution {
public:
    int countSubstrings(string s) {
        int ret = 0;
        // 1、创建dp表
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
 
        // 2、初始化
 
        // 3、填表
        for(int i = s.size() - 1; i >= 0; i--)
        {
            for(int j = i; j < s.size(); j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
                if(dp[i][j]) 
                    ret++; // 统计个数
            }
        }
        return ret;
    }
};

---

最长回文子串 ⭐⭐ 

5. 最长回文子串 - 力扣（LeetCode）

---

【题目解析】 

        与上一题一样。

【算法原理】

#：状态表示：

#：状态转移方程：

• 当 s[ i ] != s[ j ] 的时候：不可能是回文串， dp[ i ][ j ] = false
• 当 s[ i ] == s[ j ] 的时候：根据长度分三种情况讨论：
  • 长度为 1 ，也就是 i == j ：此时一定是回文串， dp[ i ][ j ] = true
  • 长度为 2 ，也就是 i + 1 == j ：此时也一定是回文串， dp[ i ][ j ] = true
  • 长度大于 2 ，此时要去看看 [ i + 1, j - 1 ] 区间的子串是否回文： dp[ i ][ j ] = dp[i + 1][j - 1] 

#：初始化：

        因为我们的状态转移方程分析的很细致，因此无需初始化。

#：填表顺序：

        根据「状态转移方程」，我们需要「从下往上」填写每⼀行，每⼀行的顺序无所谓。

#：返回值：

        根据「状态表示和题目要求」，我们需要返回 dp 表中 true 的个数。 

---

C++ 算法代码  

class Solution {
public:
    string longestPalindrome(string s) {
        int ret_max = 0;
        int begin_index = 0;
        // 1、创建dp表
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
 
        // 2、初始化
 
        // 3、填表
        for(int i = s.size() - 1; i >= 0; i--)
        {
            for(int j = i; j < s.size(); j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
 
                if(dp[i][j] && j - i + 1 > ret_max) 
                {
                    ret_max = j - i + 1 ;
                    begin_index = i;     
                }
            }
        }
 
        // 4、返回值
        return s.substr(begin_index, ret_max);
    }
};

---

回文串分割Ⅳ⭐⭐⭐ 

1745. 回文串分割 IV - 力扣（LeetCode）

---

【题目解析】 

        与上题和上上题一样。

        因为其能够将所有的字串是否是回文的信息，保存在dp表中。所以我们只需要在前述中，最后加入一个判断。

【算法原理】

#：状态表示：

#：状态转移方程：

• 当 s[ i ] != s[ j ] 的时候：不可能是回文串， dp[ i ][ j ] = false
• 当 s[ i ] == s[ j ] 的时候：根据长度分三种情况讨论：
  • 长度为 1 ，也就是 i == j ：此时一定是回文串， dp[ i ][ j ] = true
  • 长度为 2 ，也就是 i + 1 == j ：此时也一定是回文串， dp[ i ][ j ] = true
  • 长度大于 2 ，此时要去看看 [ i + 1, j - 1 ] 区间的子串是否回文： dp[ i ][ j ] = dp[i + 1][j - 1] 

#：初始化：

        因为我们的状态转移方程分析的很细致，因此无需初始化。

#：填表顺序：

        根据「状态转移方程」，我们需要「从下往上」填写每⼀行，每⼀行的顺序无所谓。

#：返回值：

        根据「状态表示和题目要求」，我们需要返回 dp[0][i - 1] && dp[i][j] && dp[j + 1][s.size() - 1] 循环判断。 

---

C++ 算法代码

class Solution {
public:
    bool checkPartitioning(string s) {
        
        // 1、创建dp表
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
 
        // 2、初始化
 
        // 3、填表
        for(int i = s.size() - 1; i >= 0; i--)
        {
            for(int j = i; j < s.size(); j++)
            {
                if(s[i] == s[j])
                    dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
            }
        }
 
        // 4、返回值
        for(int i = 1; i < s.size() - 1; i++)
        {
            for(int j = i; j < s.size() - 1; j++)
            {
                if(dp[0][i - 1] && dp[i][j] && dp[j + 1][s.size() - 1])
                    return true;
            }
        }
        return false;
    }
};